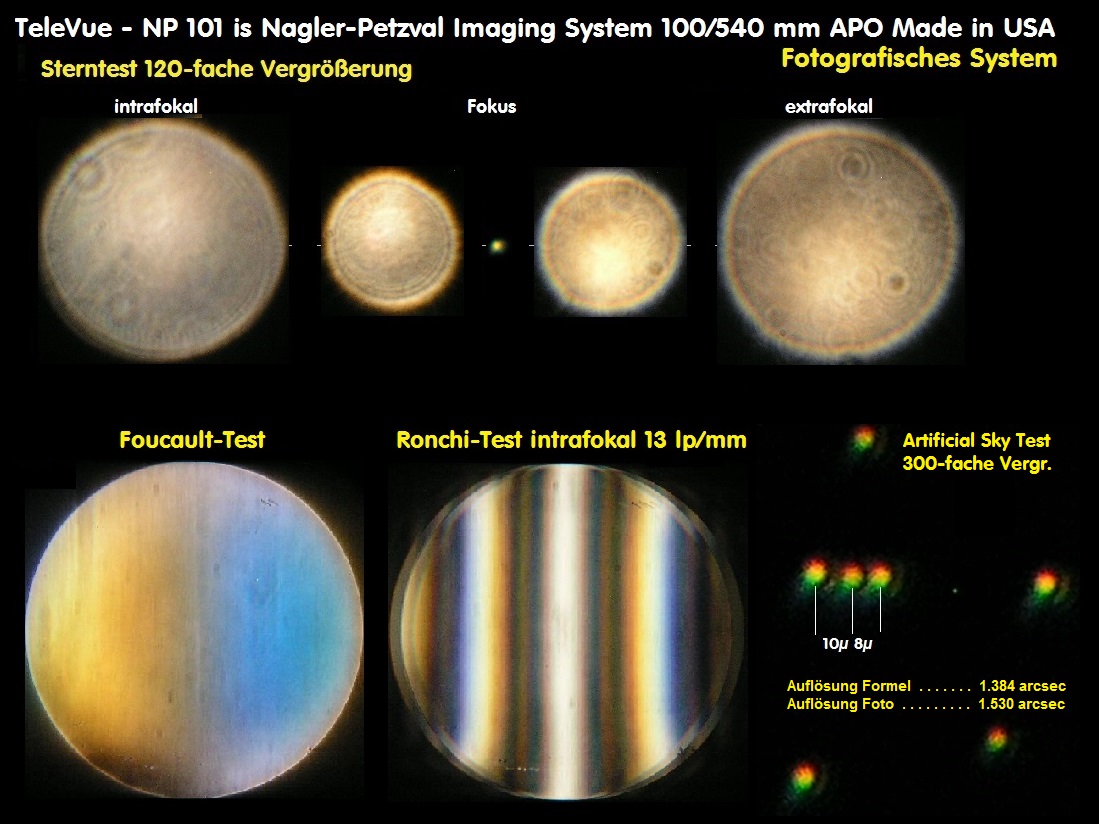
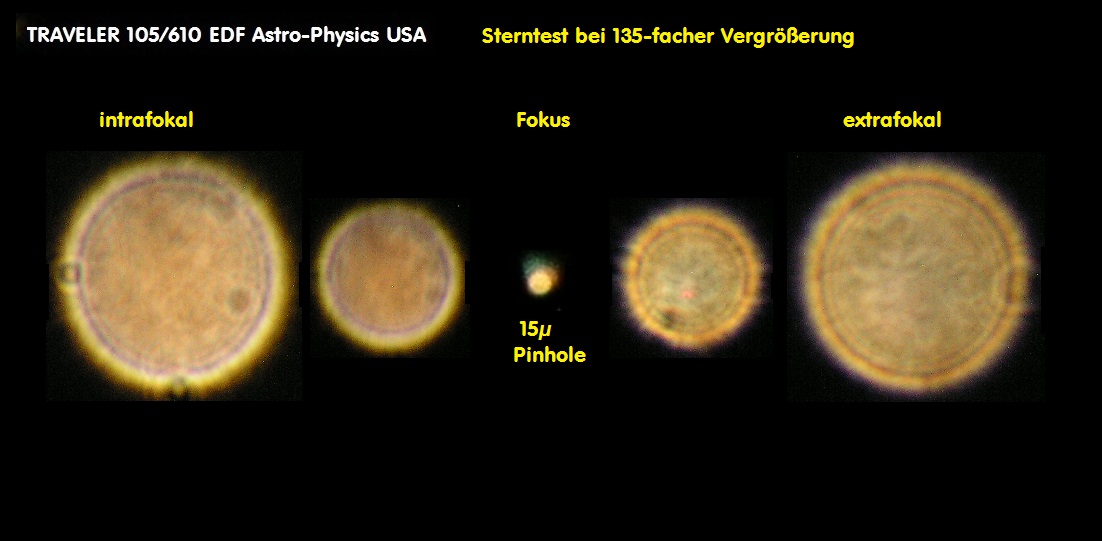
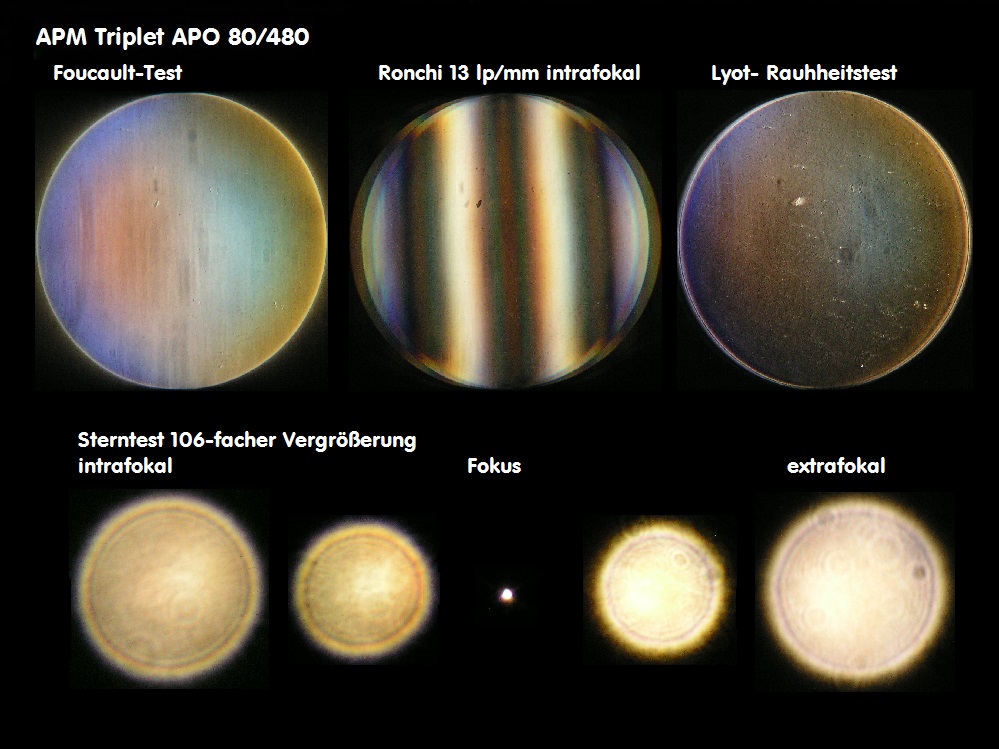
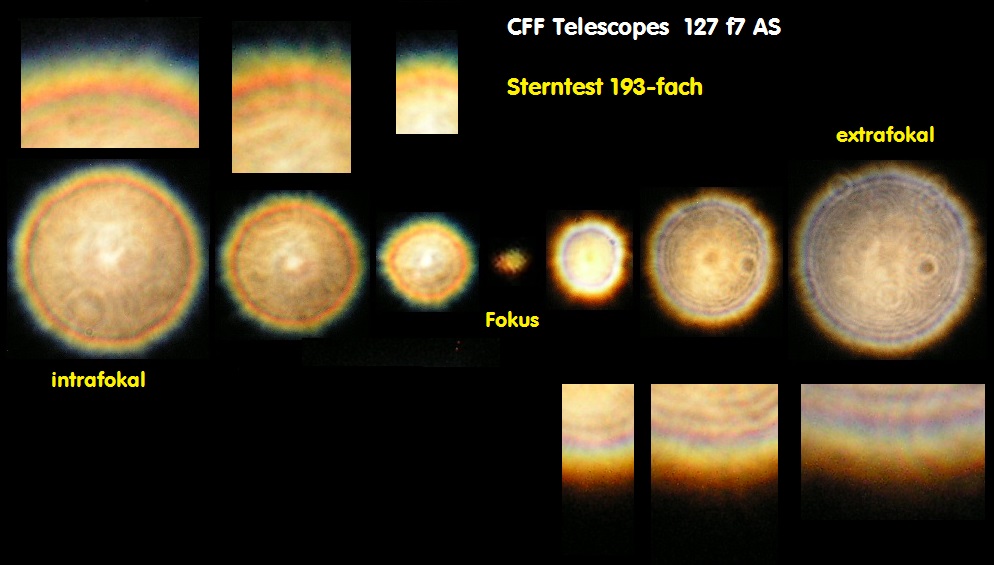
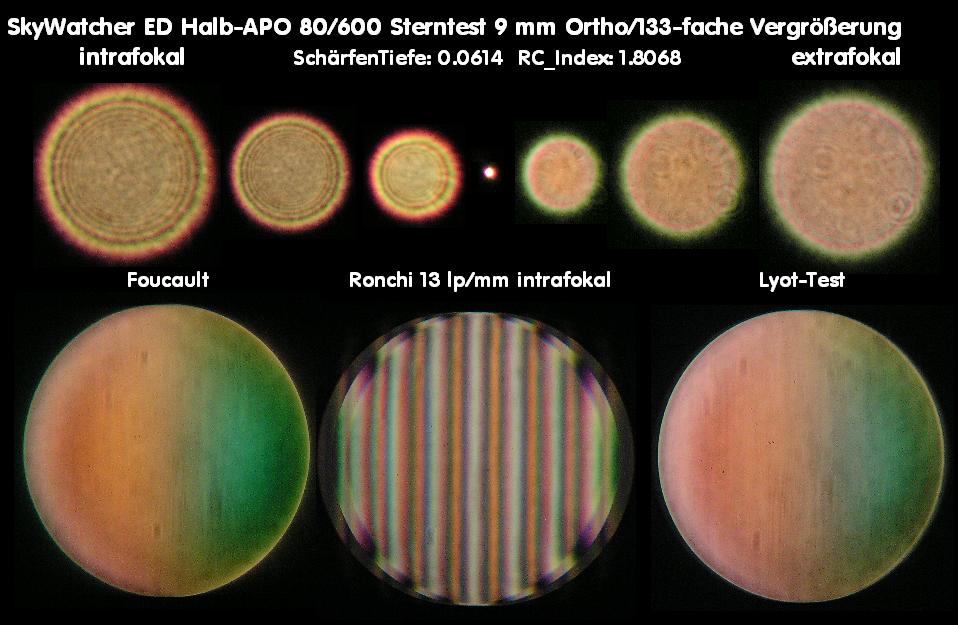
05 Messtechnik - Teil 1
E086 * Meßtechnik - etwas gründlicher, bitte !
E086 * Meßtechnik - etwas gründlicher, bitte !
Zur opt. Qualitäts-Beurteilung sollte man N I E die Ergebnisse eines einzelnen Testes heranziehen wollen, egal um welchen Test es sich handelt.
Im vorliegenden Fall hat ein von sich überzeugter Sternfreund mit guten Kontakten zu Zeiss geglaubt, ein Interferogramm mit einem Bath-Inter-
ferometer würde bei der Beurteilung eines Refraktor-Objektivs ausreichen, damit der Besitzer dieses Takahashi-Fluorit-Objektivs beim Händler
naßforsch reklamieren könne. Es gilt in jedem Fall das Prinzip:
Ein opt. System mit nur einem Testaufbau beurteilen zu wollen, ist prinzipiell falsch.
In jedem Testaufbau stecken prinzipielle Fehler, die mehr mit dem Testaufbau, und weniger mit einem optischen System zu tun haben. Und nur
wenn über unterschiedliche Prüfungen ähnliche Befunde zustande kommen, gewinnt man die Sicherheit, daß ein erkannter optischer Fehler
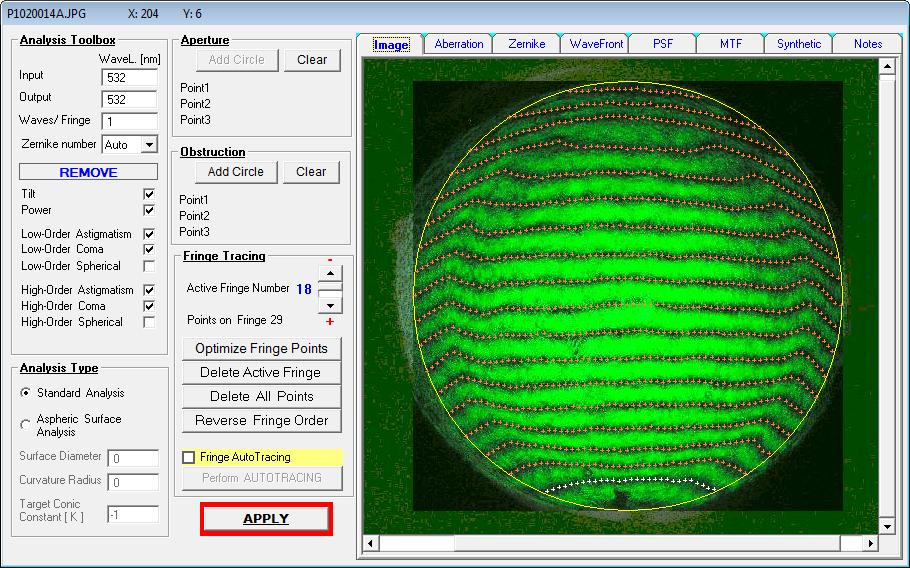
auch tatsächlich vorliegt. Der Prüfer - noch neu im Geschäft - hat also über ein Interferogramm mit dem Bath-Interferometer Koma festgestellt,
wobei auf dem erstellten Datenblatt schon nicht mehr ersichtlich ist, in welcher Wellenlänge gemessen worden ist: Entweder bei 532 nm wave,
wie im Text erkennbar, oder bei 656.3 nm wave, wie im Bild erkennbar. Bei einem Refraktor wäre das wegen des Gaußfehlers von großer Bedeutung.
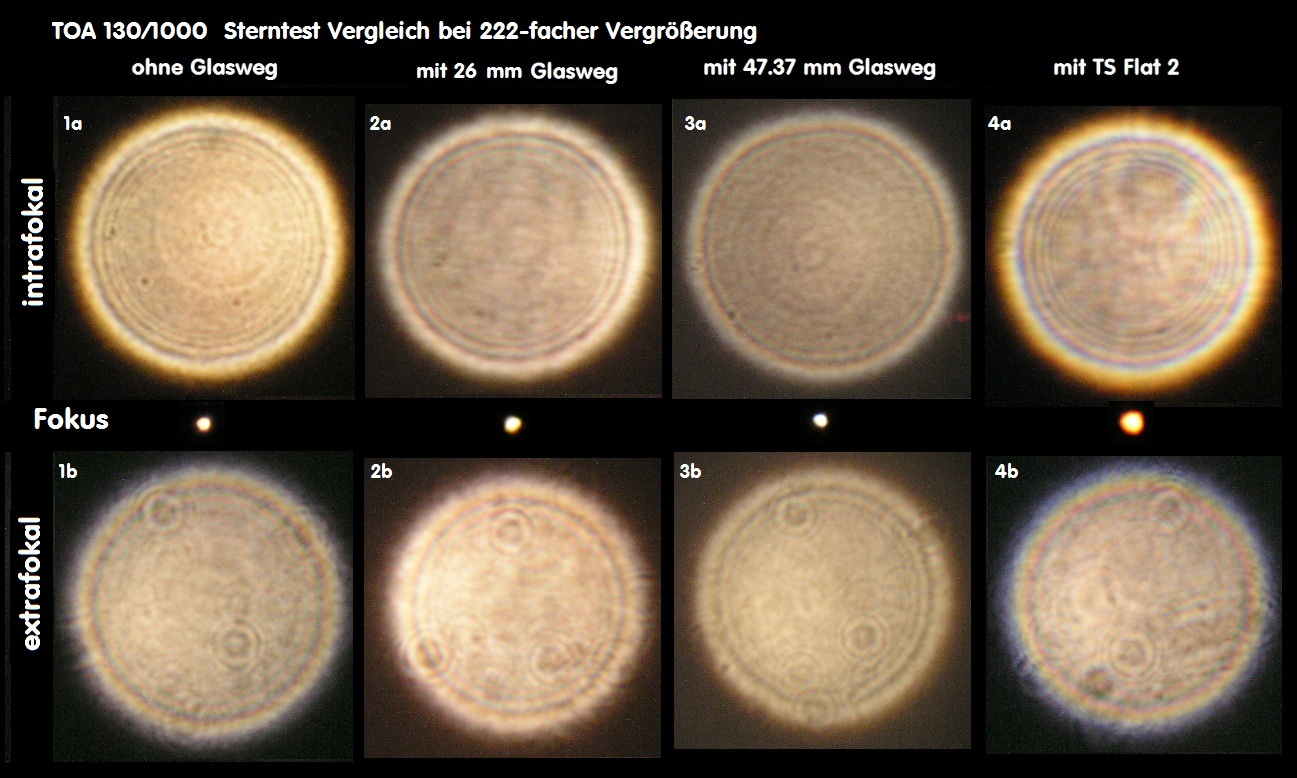
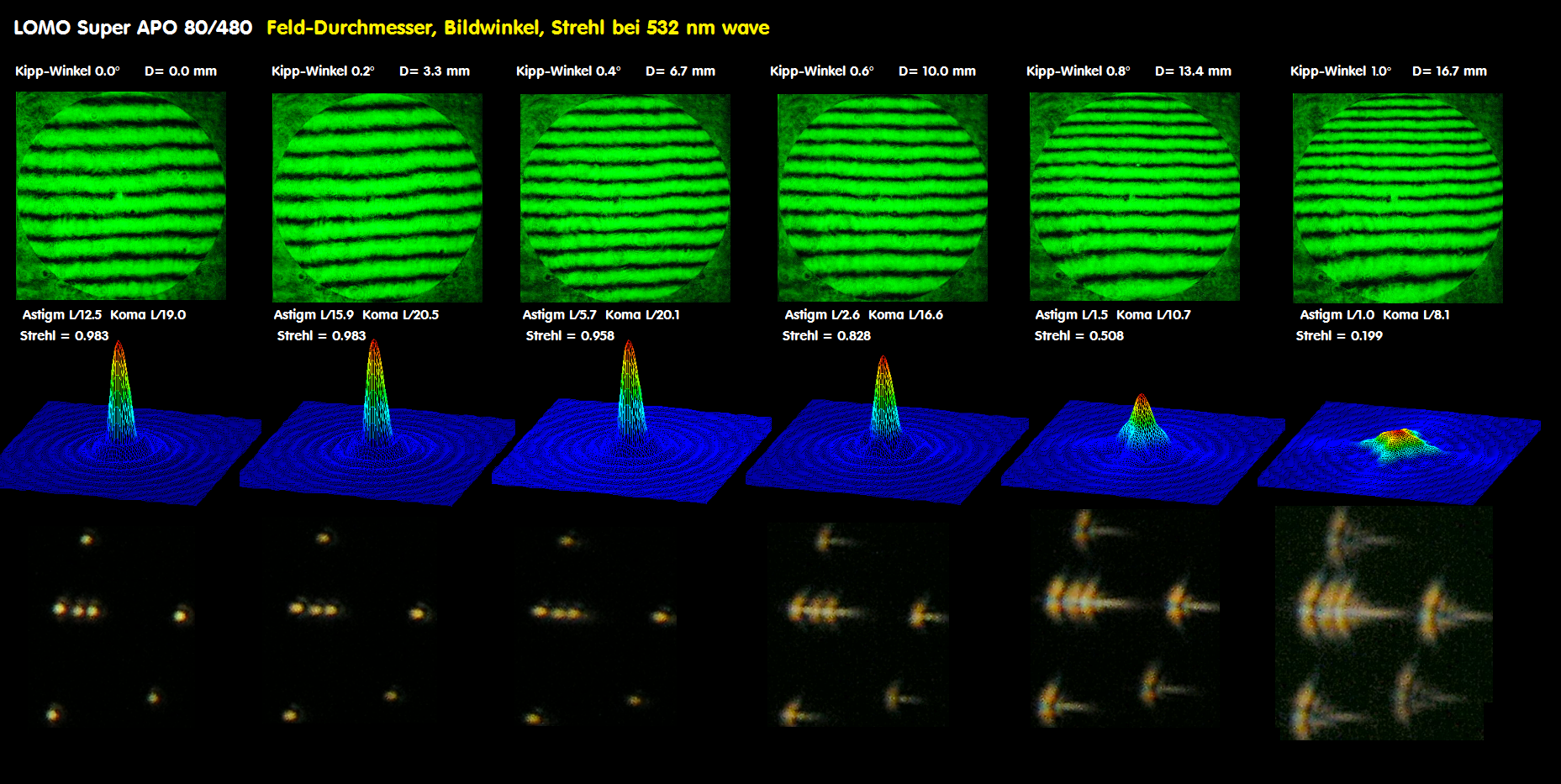
Im Zusammenhang mit der Astro/Feld-Fotografie interessiert die Abbildung von Sternen im Bildfeld, die möglichst auch punktförmig, wie auf
der opt. Achse sein sollte - es aber nicht ist, weshalb eine Reihe von guten Feldkorrektoren angeboten wird. Aus diesem Grunde ist es interessant,
zu wissen, welche Fehler im Bildfeld entstehen, auch wenn ein Objektiv grundsätzlich nur auf der opt. Achse qualifiziert wird. Wenn also einer,
ein Objektiv nur leicht verkippt, mißt er bereits nicht mehr auf der opt. Achse. Da taucht dann Koma oder Astigmatismus auf und sofort ein Grund,
ein Objektiv für minderwertig zu erachten - solche Leute gibt es leider immer wieder.
Die folgende Übersicht wäre ein solches Beispiel, welche Fehler im Bildfeld ein auf der opt. Achse perfektes Objektiv haben kann.

Je nach Hersteller bzw. Design können die Werte für Koma und Astigmatismus verschieden ausfallen, und solange sich eine Achskoma
erhärtet, weil das Objektiv auf der Achse nicht exakt zentriert ist, muß sich der Prüfer fragen lassen, ob er sich sicher ist, überhaupt auf der
opt. Achse gemessen zu haben, und nicht etwa im Bildfeld. Das passiert bereits, wenn das Objektiv zum Tubus nicht exakt kollimiert worden
ist. Für eine belastbare Aussage reicht also ein einzelnes Interferogramm bei einem Refraktor in keinem Falle aus. Im folgenden Bild sind
die Ergebnisse von Interferogramm und künstlicher Sternhimmel auf der opt. Achse und im Bildfeld dargestellt.
Im nächsten Beispiel wurden unterschiedliche Refraktoren miteinander verglichen.

Schließlich versuchen manche der Händler Konkurrenzprodukte schlecht-zu-reden, was ihnen in der Regel aber
als unsportlich ausgelegt wird.
F127A Vergleich unterschiedlicher Interferometer
Der Verfasser hat sich in über 20 Einzelberichten intensiv mit den unterschiedlichen Typen von Interferometern befasst, hat die Feinheiten
im täglichen Umgang zu ergründen versucht auf der Suche nach dem besten Interferometer-System. Gelandet ist er jedoch immer wieder
beim Bath-Interferometer: Dort kann man Interferogramme über das gesamte sichtbare Spektrum erzeugen und dessen Interferogramme
sind äußerst kontrastreich. Weil dieser IMeter jedoch nicht exakt auf der opt. Achse "arbeitet" entsteht ab einem größeren Öffnungsverhält-
nis von f/4 ein leichter Astigmatismus von PV L/3.451 , der sich nach der Formel von Dave Rowe berechnen läßt. Also nur bei Systemen grö-
ßer F/4 könnte man im äußersten Fall den Astigmatismus bei der Auswertung z.B. AtmosFringe deaktivieren. Bei kathadioptrischen Systemen
muß man jedoch auf der opt. Achse messen, da sich sonst die Vignettierung zu deutlich auswirkt. Eine Übersicht ganz unterschiedlicher Interferometer
findet man hier.
Die opt. Komponenten für die nachfolgenden Bau-Typen kosten in der Regel nicht mehr als 500.- bis 600.- Euro. Wer jedoch einen fertigen
Interferometer bezahlen muß, darf dafür mehr als das Vierfache bezahlen. Als ehemaliger Feinmechaniker bin ich deshalb nicht auf fremde
Hilfe angewiesen.
Massimos Bath-IMeter mit WeißlichtMassimos Bath-IMeter mit Weißlicht , Stoffies Bath IMeter , Ceravolo Interferometer ,
Massimos Twyman-Green IMeter , Scattered plate Interferometer - Benischeck , Point Diffraction Interferometer , 2, Link , 3. Link ,
Der Twyman-Green Interferometer
Mit diesem Interferometer hat sich der Autor etwas zwei Stunden lang beschäftigen dürfen. Leider ohne eigene IGramme damit erzeugen
zu können. Zunächst soll man an der Laser-Hülse links mit einem Laser-Chesire Okular die grobe Richtung einstellen. Anschließend
wird in die gleiche Hülse ein künstlicher Stern eingesteckt und am mittleren/unteren Ausgang mit einem Okular zentriert. Damit ist
aber leider die 3. Achse, der exakte Fokus-Punkt des Interferometers nicht bestimmt, sodaß man im günstigsten Fall kleine kreis-förmige
Igramme erhält, ein Hinweis darauf, daß man den Fokus verfehlt hat. Von meinem eigenen Twyman-Green weiß ich, daß auch der exakte
Fokuspunkt wichtig ist, wenn man nicht zuviel Zeit mit Suchen verlieren will. Auch taucht bei diesem IMeter das Problem der Licht-Quelle
auf. Die Schwankungen liefern im Wechsel kontrast-reiche/-arme Interferogramme ab. Ich vermute, daß man dies nur mit einer stabilisieren
Laserdiode lösen kann. Hauptkritik ist also das umständliche Suchen, bis das System interferiert. Nur wenn alles drei Koordinaten exakt
zusammenfallen, bekommt man Interferogramme. In meinem Fall habe ich das so gelöst, und wußte auch über ein gleichbleibendes Okular,
wo genau der Fokus liegt. Mit demBath-IMeter hat man es da wesentlich einfacher.

Das Einrichten (align) dieses Twyman-Green-IMeters ist beschwerlich, wenn man kein einfaches Verfahren hat, die beiden Lichtpunkte räumlich
zueinander zu führen. Das mindert schon erheblich die Lust einer qantitativen Messung einer Optik vor dem Planspiegel. Es entstehen dann,
vermutlich abhängig von der nicht stabilisierten Lichtquelle des Lasers unterschiedlich kontrastreiche Interferogramme, sowohl bei dem fremden
IMeter als auch bei meinem erkennbar.
Ein ganz wesentliches Merkmal zwischen Bath- und Twyman-Green-IMeter ist jedoch die Genauigkeit der opt. Komponenten:
Während beim Bath-IMeter sich Fehler in Teilerwürfel und Bikonvex-Linse durch die Doppelbenutzung kompensieren, muß
beim Twyman-Green-IMeter der Teilerwürfel ohne Fehler sein. Astigmatismus würde man sofort im Ergebnis erkennen. 
Bei der räumlichen Zentrierung des GRZ-Twyman-Green-Interferometers müssen die beiden Lichtpunkte in X, Y und Z zur Deckung gebracht
werden, damit Interferogramme entstehen. Besonders der richtige Fokus ist ein Problem - weil er mit einem Okular gelöst werden muß. Dabei
sollte das Okular unbedingt auf den ersten feststehenden Punkt fokussiert werden, damit man den Fokus des zweiten, von der Prüfoptik
kommenden Punkt findet. Man sollte deshalb immer das gleiche Okular verwenden, und auch den Fokus des ersten Bündels, das von Laser-
modul, Pinhol, Teilerwürfel und Planspiegel erzeugt wird, vorher einstellan kann. Eine Besonderheit bildet der kleine Planspiegel hinter dem
Teilerwürfel. Bei dieser Variante liegt der Fokus des 1. Bündels etwas näher am Betrachter, was aber prinzipiell optisch nicht stört. In meinem
Fall ist das eine kleine Sphäre. 
Bei meiner Bauweise wird das Okular räumlich, also in X, Y und Z eingestellt, also mittig auf diesen Punkt fokussiert, wie der vom Lasermodul
über eine "ball-lens" erzeugt und durch den Teilerwürfel zur Sphäre links und von dort zurück zum Okular gespiegelt wird. Der zweite Punkt, der
von der Prüfoptik zurückgeworfen wird, muß mit dem ersten zusammenfallen. 

some technical notes, choosing the best reference element
This GRZ-model uses a flat mirror as reference element. My model uses a spherical mirror, next picture, why ?
Every kind of interferometer works, if the both light points are congruent with one another in X, Y and Z. The light point at the GRZ-model
you will find it at the beginning after the laser-modul. There you have to put the second boundle/laser light point from the tested optic.
Then these two points will interfere. In this model you have much problems to find that .
Thats the reason, better to use a small sphere. This creates a seperated light point, that you better can control with an eyepiece. The second
light point from tested optic you just move to the first point in X, Y and Z, and now the systems creates interferogramms faster. 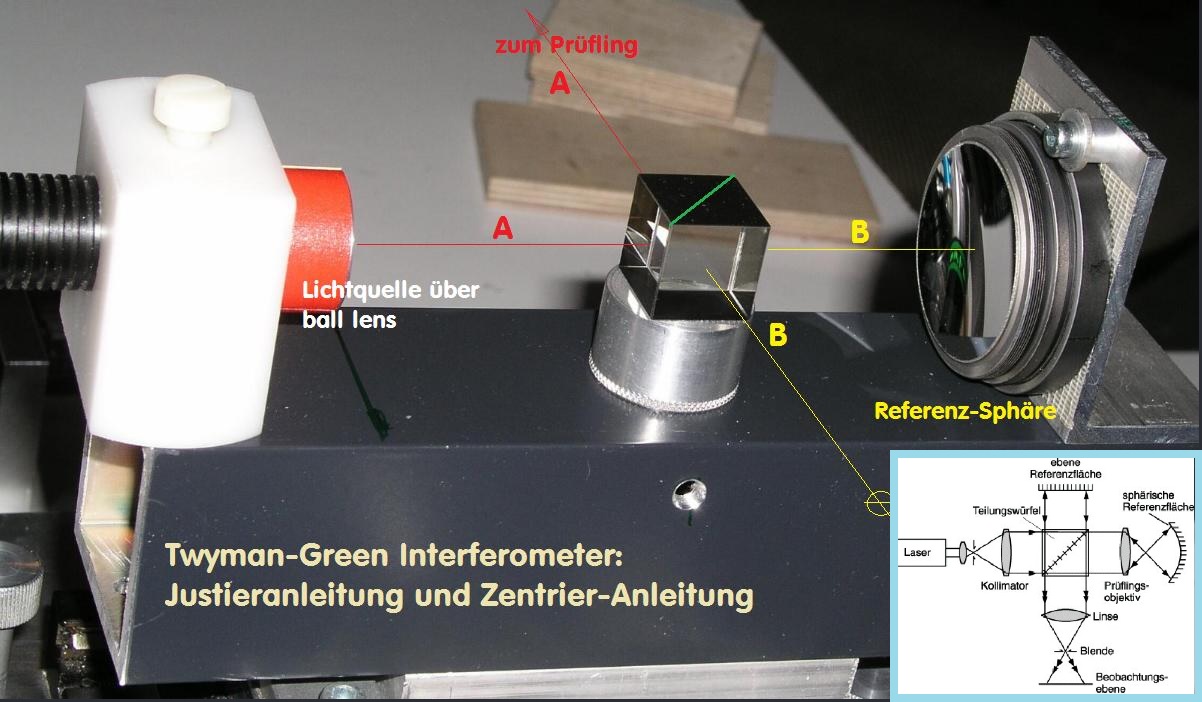
So, if anybody buys the GRZ-model interferometer, you should get an accurate instruction for use: What kind of eyepiece and the fokus of it.
Or you substitute the reference flat by the sphere.
A technical suggestion
Both boundles what interfere at the laser module beginning. So that two points they have to put together. One way for controlling that
is using a small Kepler telescope what is focuses at the first light point at the laser module. The second boundle from the tested optic can
controlled till it is at the same position. 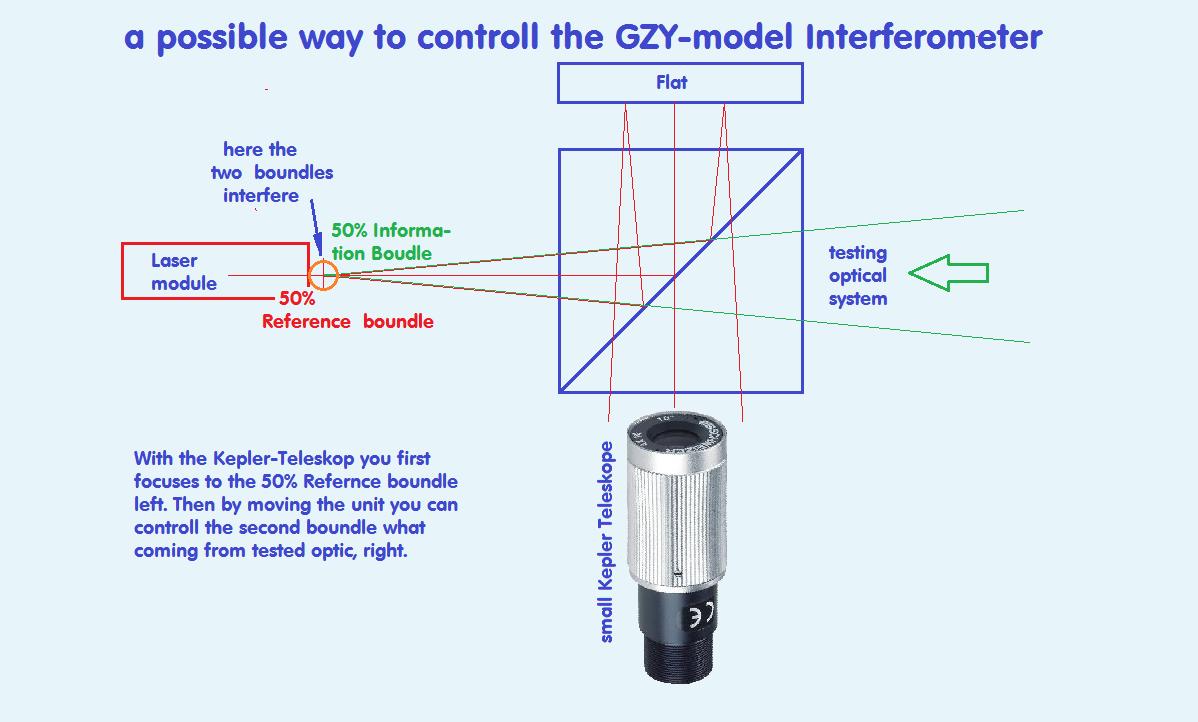
F142-01 Kreuztisch und andere Zusatzgeräte

Kreuztisch für die Mikroskopie Zanger & Söhne
E059B * Seeing in Theorie und Praxis bei Teleskopen
https://www.astrotreff-deep-sky.de/posts/t6824-Grundsatzliches-zum-Seeing-noch-ein-Versuch--
Die Annahme, daß man mit großen Teleskop-Öffnuungen auch hohe Vergrößerungen erzielen könnte ist falsch. Selbst wenn
eine Optik noch so perfekt wäre, wie im Falle meines ausgesuchten C11, siehe Bild, und selbst wenn sich aus meinen Messungen
auf der opt. Bank eine perfekte Auflösung am Himmel erwarten läßt, sind z.B. am Saturn nur in seltenen Ausnahme-Fällen
Vergrößerungen über 200-fach möglich, was man leicht an der "kantenscharfen" Cassini-Teilung/Saturn erkennen kann.

https://www.meteoblue.com/fr/meteo/prevision/seeing/ha%C3%9Ffurt_allemagne_2909335
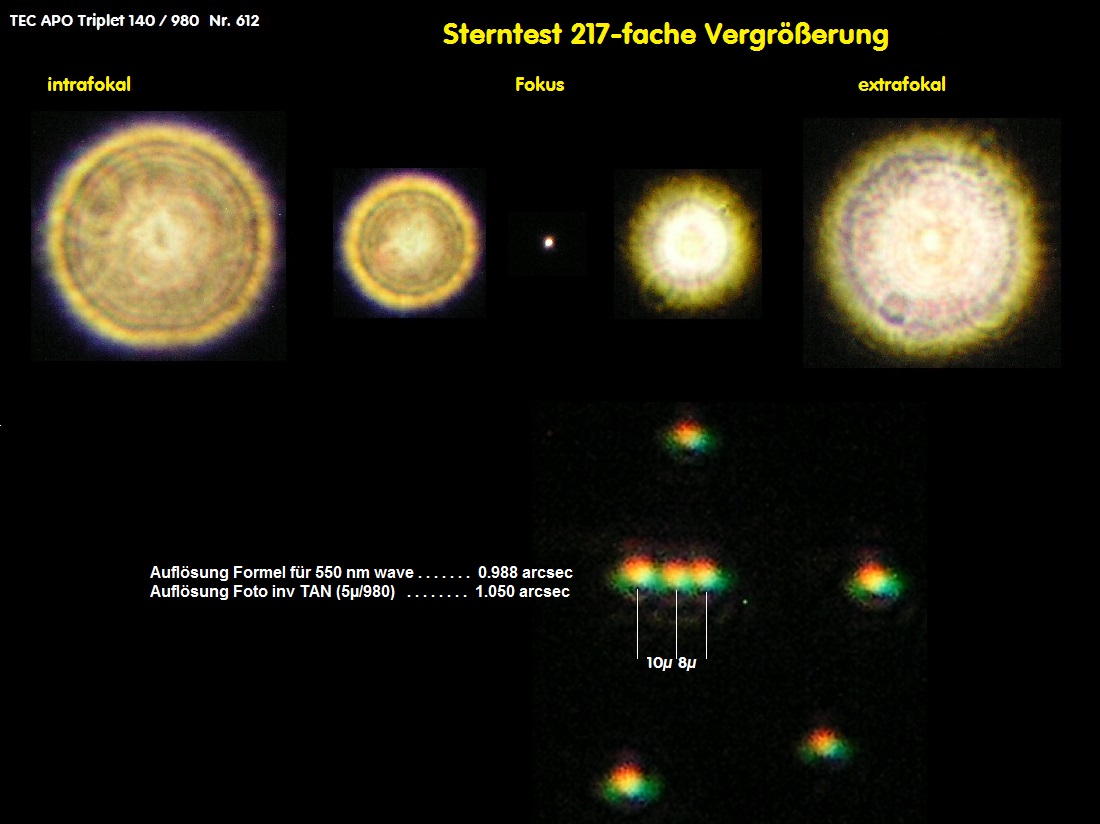
Warum ist das eigentlich so? Sowohl die Auflösung nach der Formel für 550 nm wave 138.4038 / D, aber auch über das Foto meines
Artificial Sky Testes, Bild weiter unten, beweist, daß dieses C11 eine Auflösung von ca. 0.5 arcsec hat. Damit wäre also die Cassini-
Teilung am Saturn immer kantenscharf, müßte also brilliant zu sehen sein. Bereits das nächste Bild für das Astronomische Seeing in
Hassfurt im Main-Tal reduziert das Seeing auf bestenfalls 1.xxx arcsec. Die mögliche opt. Auflösung meines C11 scheitert also an den
atmosphären Bedingungen meines Standfortes. Dazu kommt, daß unsere Region unter dem Knotenpunkt zweier Luftfahrtlinien liegt,
Frankfurt/Berlin bzw. München/Hannover mit ca. 1000 Flugewegungen und die für mich überflüssigen Kondenzstreifen, die einen am
Morgen noch relativ klaren Himmel förmlich zunäht, sodaß am Abend über uns eine "milchige Suppe" herrscht. Das Flußtal im Main
hatte lange Zeit noch das Kernkraftwerk in Grafenrheinfeld zu ertragen, bzw. die Wasserdampf-Schwaden, die ostwärts flußaufwärts
zogen. Auch haben wir zwischen Tal und umliegendem Steigerwald bzw. Haßberge eine Temperatur-Differenz von ca. 1 - 2° C, wenn man
vom Tal in die "Berge" fährt. Der Saturn stand vor 10 Jahren höher am Himmel, aber auch da waren die Möglichkeiten einer Vergrößerung
über 300-fach bei meinen 12.5 Newton mit excellentem LOMO-Spiegel und hochwertigen Fangspiegel nur selten zu realisieren: Nach
einer Auskühlzeit von mehreren Stunden, klappte ich oft den Deckel meines Newton wieder zu, weil das Seeing leider nicht zu ändern
war. Es nützt also wenig, auf einer PV L/10 Optik zu sistieren. Wer unerfahren in der Praxis ist, wird nie ein Fernrohr finden, das seinen
Wünschen entspricht. Der gute Amateur-Astronom sollte sich zunächst darüber informieren, welches astronomische Seeing sein
Standort überhaupt zuläßt und der obere Link von Meteoblu könnte dabei helfen. 
Die Pickering Seeing-Skala
http://r2.astro-foren.com/index.php/de/16-beitraege/08-berichte-teleskop-treffen-haeufige-fachbegriffe/729-h140-pickering-seeing-skala
Hier findet man eine animierte Version der Pickering Seein-Skala der Intesität atmosphärischer Turbulenzen. Angefertigt wurde sie mit
Aberator V2, und unter Nutzung von Pickering's Bewertungen betreffs der Auswirkungen dieser Turbulenzen auf das Airy-Scheibchen.
Dies ist Grundlage dieser Abstufungen. Diese Skala wurde von William H. Pickering (1858-1938) unter Hinzunahme eines 5" (13cm)
Refraktors erstellt. Die Animationen wurden von Damian Peach erstellt.











Über den Artificial Sky Test läßt sich die Auflösung bei 1555-facher Vergrößerung bei perfektem Seeing auf der opt. Bank wunderbar berechnen:
Während in diesem Beispiel nach der Formel für 550 nm wave ein Wert von ca. 0.5 arcsec herauskommt, liegt die Auflösung ebenfalls im gleichen
Rahmen, wie sich über das Foto beweisen läßt. Trotzdem führt die Gesamtsumme aller Einfluß-Faktoren zu allerhöchstens 1 arcsec seeingbedingt
und über weitere Einflüsse dann noch niedriger. Viele Streitigkeiten, mit wem auch immer, könnte man also vermeiden, wenn man etwas mehr
Erfahrung hätte. 
Es muß ja einen Grund haben, wenn sich europäische Astronomen ausgerechnet auf dem Cerro Armazones ca. 132 km südlich von
Antofagasta, Chile; ihr neues Großteleskop bauen. Dort hat die RUB ihr Hexapod und ca. 15 km davon entfernt sind auf dem Paranal
vier weitere 8-Meter Spiegel. Auch von dort sind ständige Seeing-Messungen während einer Beobachtungsnacht bekannt.
Auch auf der opt. Bank kann man Seeing gut darstellen: http://rohr.aiax.de/IGramm_Seeing.avi
Vor ca. 10 Jahren fand man auf den Webseiten der ESO noch die tägliche Übersicht über das dort herrschende Seeing. Mittlerweile
wurde es von diesen Übersichten abgelöst: http://www.eso.org/gen-fac/pubs/astclim/paranal/
http://www.eso.org/gen-fac/pubs/astclim/paranal/seeing/
E085 * Ross-Null-Test / Kompensation einer Hyperbel
Vorbemerkung bzw. der Anlaß (überarbeitet am 16.09.17, am 22.09.17)
August 2017 erreichte mich ein hyperbolischer Hohlspiegels mit Durchmesser 396 mm und 2391 mm Radius im Ursprung. Der Hersteller
jedoch weigerte sich, einen genauen Nachweis zu führen, welche konische Konstante dieser Hauptspiegel denn nun hätte. Im Design wird
eine konische Konstante von - 1.5 verlangt, die von der Firma offenbar nicht erreicht worden war - jedenfalls entstanden im System keine
entsprechenden Punktabbildungen besonders im Bildfeld. Ich wurde deshalb gebeten, die konische Konstante am konkreten Spiegel zu
ermitteln:
http://r2.astro-foren.com/index.php/de/berichte/05-messtechnik-teil-1/2-uncategorised/773-e084-hyperbel-konische-konstante-und-zonenfehler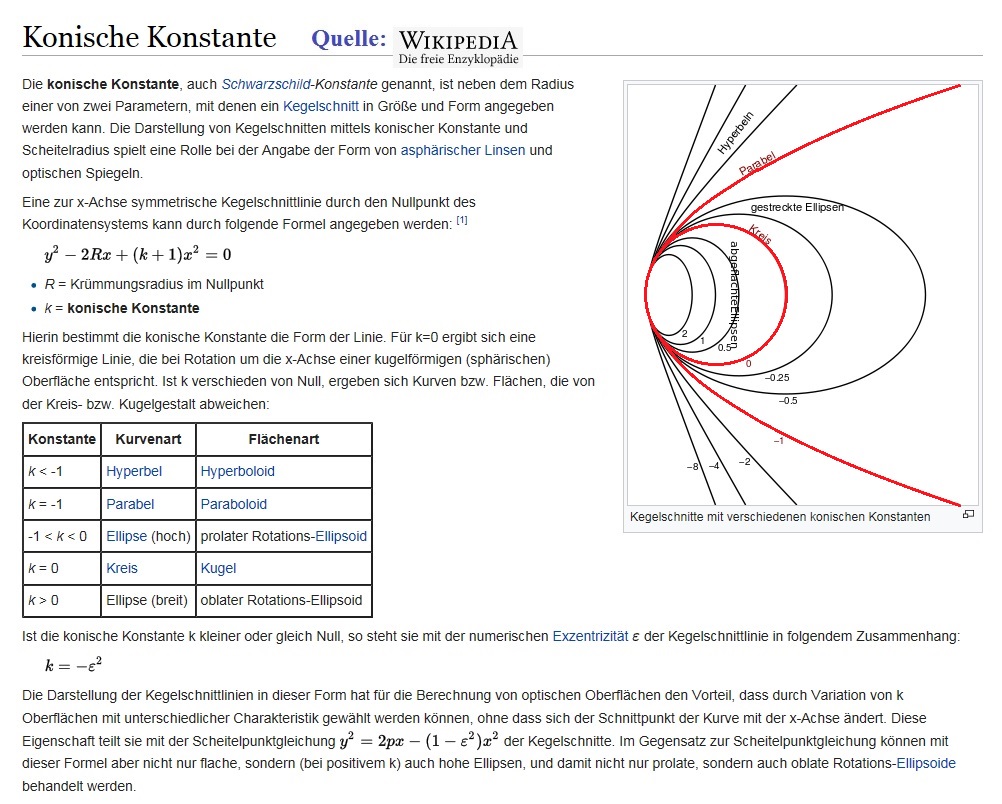
Die Lösung über den Ross-Null-Test:
Beim Ross-Null-Test folgt auf die Lichtquelle links eine Plankonvex-Linse und danach der Hyperbolspiegel. In einem errechneten Abstand,
siehe das folgende Datenblatt in ZEMAX, kompensiert die sphärische Aberration der Linse die sphärische Aberration des Hyperbol-Spiegels
auf Null. Das Programm optimiert auf die richtigen Abstände und die richtige Conic constant.
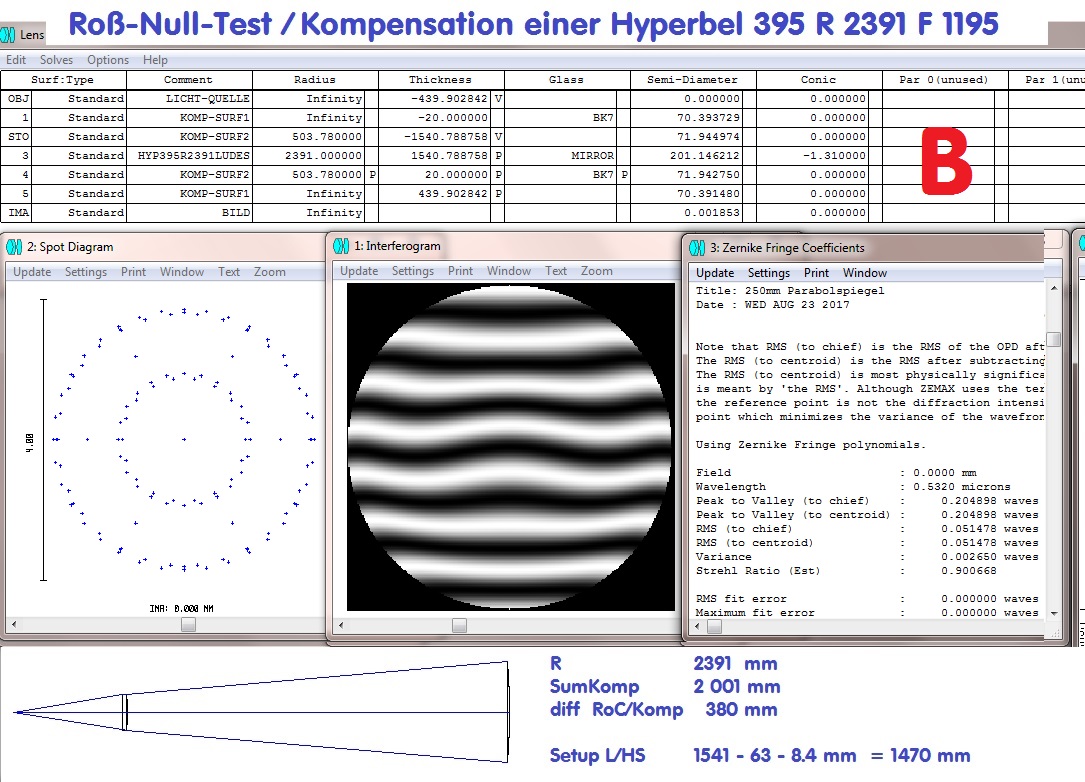
Das folgende Foto zeigt den Testaufbau, wie er sich aus dem oberen ZEMAX-Datenblatt ergibt. 
Versuch einer mathematischen Näherung
Wer kein ZEMAX zur Verfügung hat kann sich auch mit dieser mathematischen Näherung behelfen: Dabei ist zunächst der Graph der
Hyperbel definiert aus Einfallshöhe "h", dem Mittelpunkts-Radius "R" und der konischen Konstante "k". Im Punkt "h" wird an den
Graph eine Tangente und dazu eine Normale gezeichnet/gerechnet. Die Normale in Punkt "h"schneidet die Rotations-Achse (Hyperbo-
loid) in einem größeren Abstand, und so entsteht die gesuchte Schnittweiten-Differenz zwischen dem Mittelpunkts-Strahl und dem
Randstrahlen der Hyperbel. Dieser Abstand läßt sich entweder über den Foucault- oder den Interferometer-Test ausmessen, wie weiter
unten gezeigt wird. Damit läßt sich die tatsächliche konische Konstante des Spiegel mit einiger Sicherheit ermitteln. Die Lösung über
den Ross-Null-Test erscheint mir aber genauer zu sein.
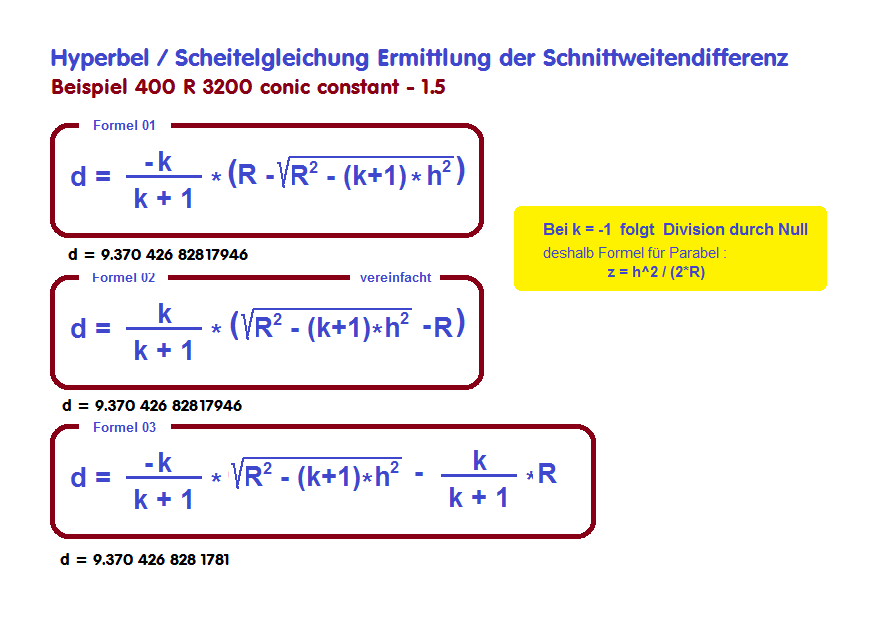
Der Graph dieser Hyperbel (in folgender Zeichnung) definiert sich also über den Mittelpunkts-Radius von 3200 mm und der konischen Kon-
stante von - 1.5 und dem 1/2 Durchmesser von 399.222 mm = "h" = 199.611 . In diesem äußersten Punkt "h" wird eine Tangente gezeichnet
und dazu im gleichen Punkt die Normale, die sich im Beispiel mit einer Differenz von ca. 9.340 . . . mm mit der opt. Achse schneidet. Es soll
also dieser Differenzbetrag ermittelt werden zwischen der opt. Achse und der Normale bei Punkt "h". Diese Näherungs-Rechnung gilt
für alle Kegelschnitte, also Kreis, Ellipse, Hyperbel und Parabel. Siehe auch der Hinweis bei der Parabel -1.0 in der folgenden Übersicht.
(Gelber Kasten)
Die Vermessung über Interferometrie
Es muß also die Schnittweiten-Differenz zwischen Mittelpunkt- und Randstrehlen ermittelt werden. 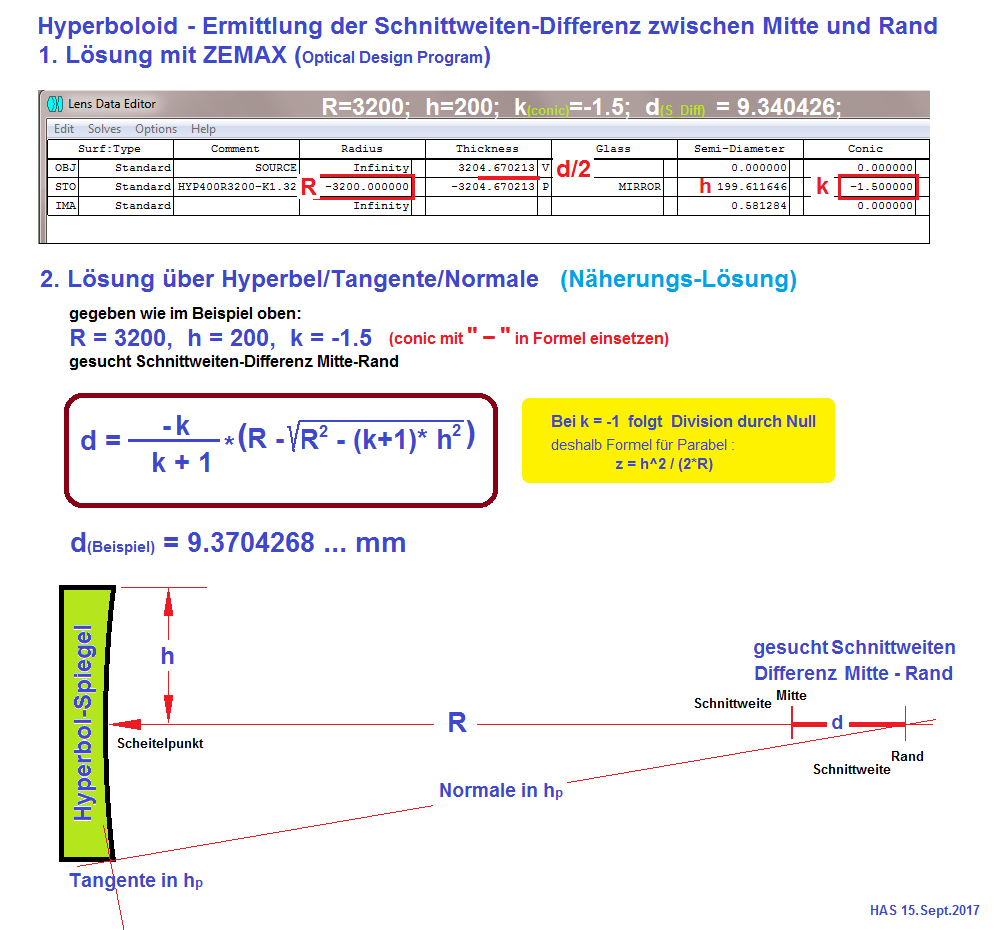
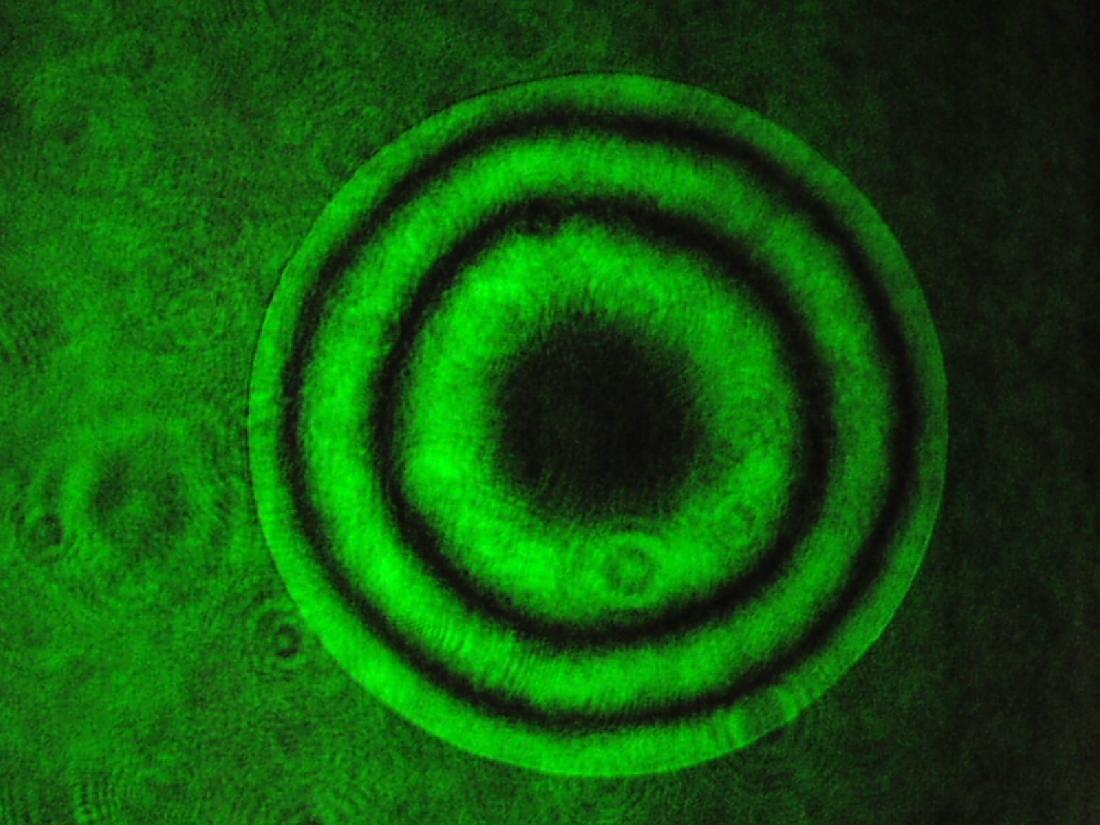
Mit den folgenden Interferogrammen kann man die Abstände ermitteln bei Mitte, 0.707-Zone und Rand. Der obere Bildteil wurde mit ZEMAX
simuliert, der untere Bildteil sind reale Fotos der gleichen Situation. Ein Grenzfall wäre die Parabel mit conic constant -1.0, bei der die Formel lautet:
z = h^2 /(2*Radius) = Formel für Pfeilhöhe der Parabel, gilt auch für Schnittweiten-Differenz der Parabel.
In der jeweiligen Zone erscheinen die mittleren Streifen waagrecht, für die Mitte sind es die Streifen im Zentrum, ebenso bei der 0.707
Zone und schließlich die Streifen am Rand. Am sichersten läßt sich das noch für die Mitte und die 0.707-Zone bestimmen, und dieser
Wert müßte dann mit " 2 " multipliziert werden. Damit kann man zu Beginn die konische Konstante ungefähr eingrenzen.
Ein weitere Möglichkeit ist die Zonen-Abstandmessung über den Foucault-Test, wie er bei Spiegelschleifern üblich ist..
Nachbetrachtung:
Ein kleines GFA-Programm zur Ermittlung der Schnittweiten-Differenz für die Hyperbel sei hier vorgestellt. Grundlage ist die obere Formel.
Am Beispiel eines Parabol-Spiegels für 400 R 3200 conic= -1.0 ergibt sich

E084 * Hyperbel - Konische Konstante und Zonenfehler
E084 *
A - Hyperbel - Konische Konstante und Zonenfehler;
B - elliptical Flat
C - andere Setups , Hindle-Sphere, Waineo-Test, Foucault-Schnittweiten-Messung, Hindle-Sphere, Waineo-Test, Foucault-Schnittweiten-Messung
AMATEUR TELESCOPE MAKING, Book one, S225, "A new test for Cassegrainian ... secondary mirrors" Mounthly Notices of the Royal Society , March 1931;
Hyperbel
Besonders bei Newton-Spiegeln taucht sie auf: Die konische Konstante mit -1 für eine Parabel. bei RC-Systemen hat man es mit zwei
Hyperbeln zu tun: für den HS eine etwas schwächere { -2.0 < Hyperbel < -1.0 }, für den Sekundärspiegel etwas stärker { -5.0 < K < -3.0 }.
Bei langebrennweitigen Spiegel-Systemen kommen Rotations-Ellipsoide vor (Dall-Kirkham/Mewlon), ebenso ist die Asphäre bei man-
chen Optiken ebenso eine Kegelschnitt-Rotations-Fläche. Im vorliegenden Fall sieht sich der Hersteller dieses Hyperbolspiegels außer-
stande, die erzielte Konische Konstante heraus zu geben, sodaß man über diverse Setups den Versuch startet, die Konstante zu ermitteln.

-
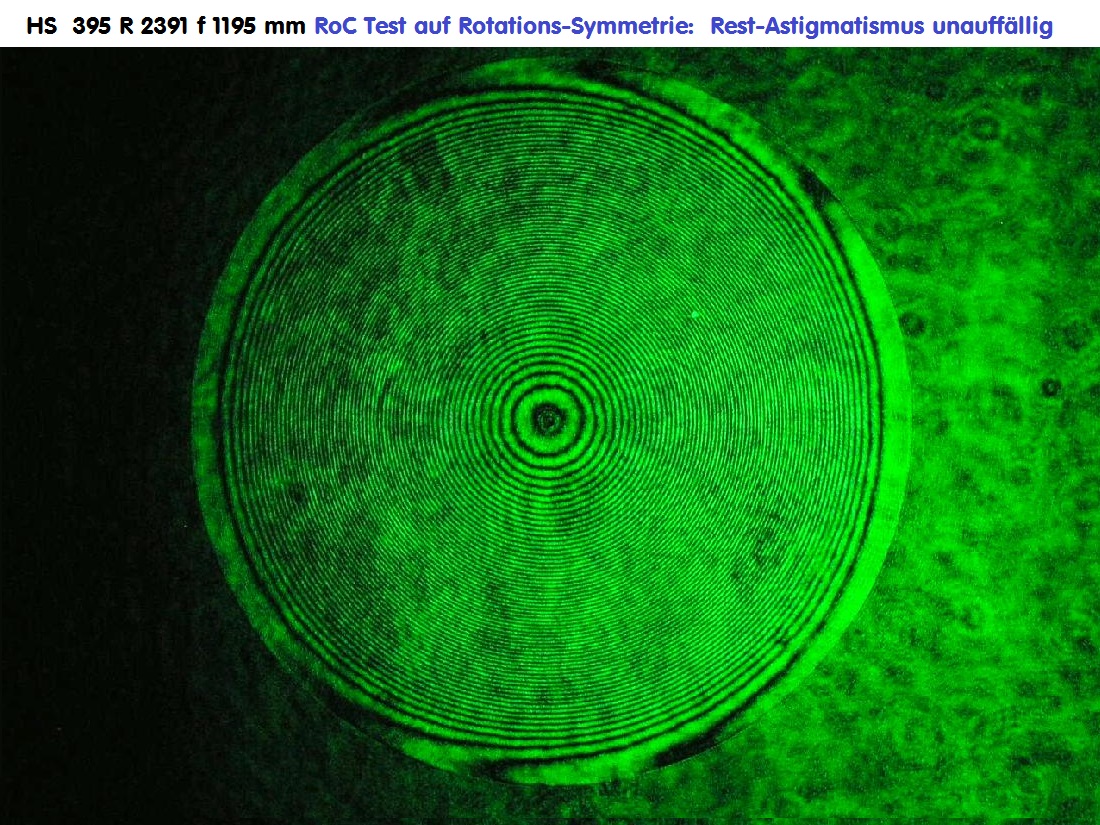
Wegen diverser Berechnungen braucht man die Spiegeldaten im Krümmungsmittelpunkt: Durchmesser 395 mm Radius im Scheitel 2391 mm.

-
Der erste Test überprüft die Rotations-Symmetrie, bzw. einen möglichen Rest-Astigmatismus. Dieser Befund ist unauffällig, aber auch
deswegen schwierig, weil wegen der Hyperbel sehr viele Streifen im Spiel sind.
-
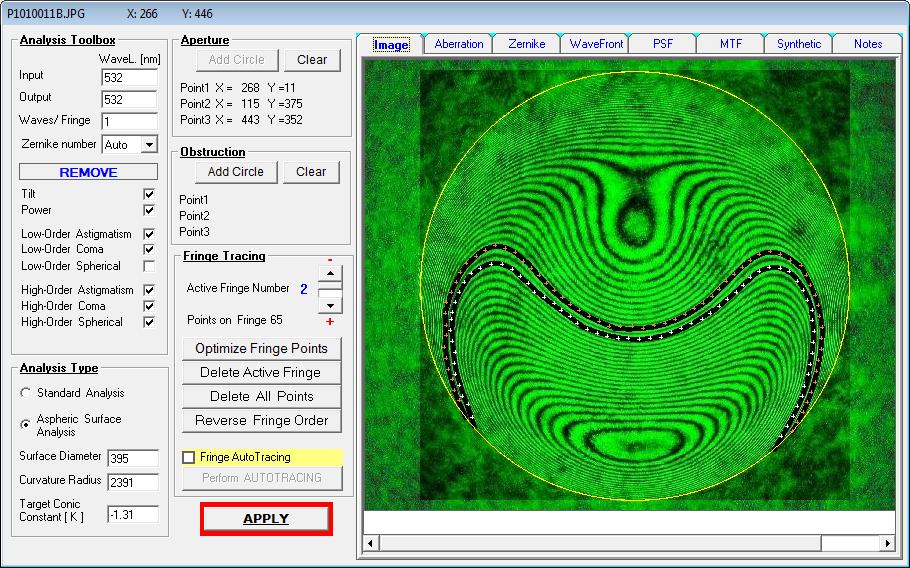
Da man über AtmosFringe in RoC eine Parabel auf Null zurückrechnen kann, geht das natürlich auch bei einer Hyperbel. Betrachtet man
für diesen Fall nur die Sphärische Aberration, dann genügen bereits zwei Streifen, um ungefähr auf die Konische Konstante zurückzurechnen.
-
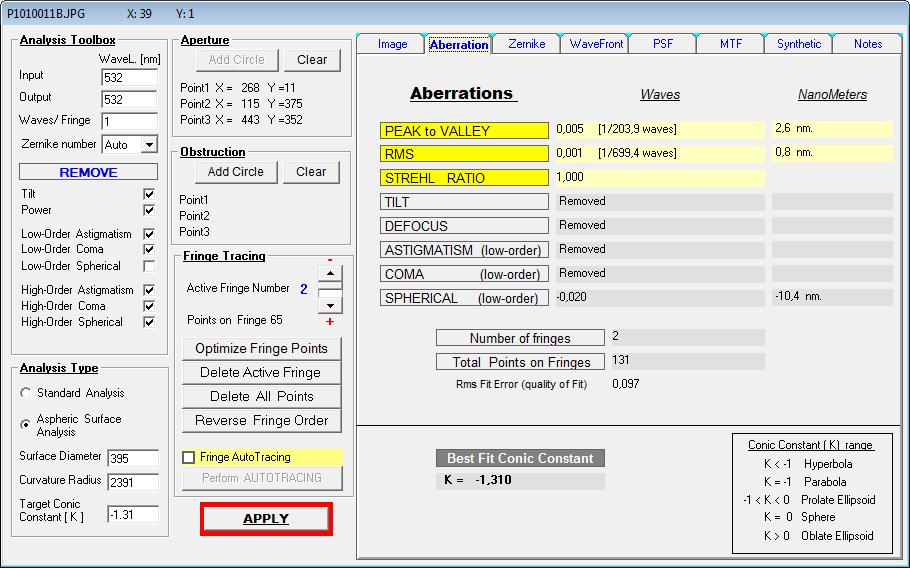
Im ersten Durchgang wären das dann K -1.310, wie im folgenden Bild zu sehen
-
Steckt man diese K = 1.310 in eine ZEMAX-Kompensations-Berechnung so ergibt sich ein HS / KompLinsen-Abstand von ca. 1541 mm.
Wäre dieser Spiegel perfekt, also ohne jede Zone und exakt der Wert K = -1.310, dann würde das Interferogramm etwa wie das untere
synthetische IGramm aussehen.

-
Passend zur oberen Berechnung also der Testaufbau mit dem errechneten Abstand 1541 mm
Der Hubtisch auf dem die Komp-Linse steht, wird seitlich durch eine Holzplatte geführt, sodaß man auf einfache Art den
Abstand Linse - Hauptspiegel variieren kann.

-
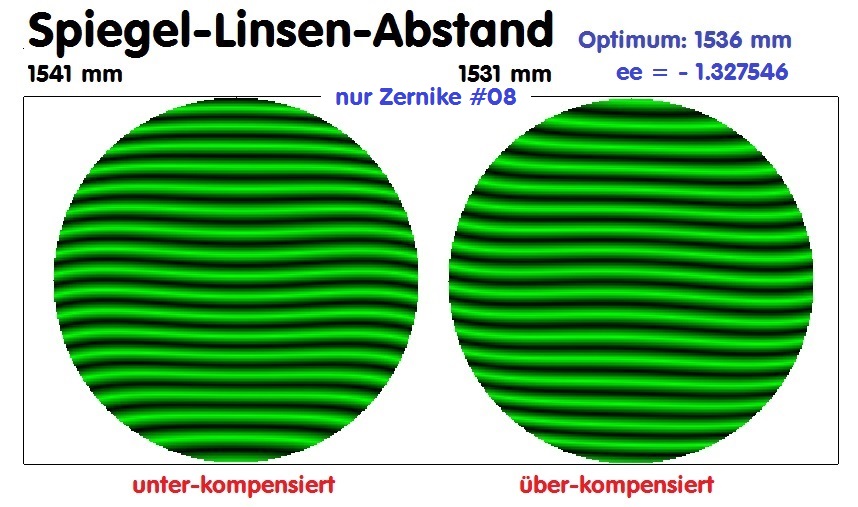
Das auffälligste Merkmal in diesem Fall wäre die Zone bei ca. 90% vom Durchmesser, eine Art Ringwall.
-
Das Ergebnis kann man sich ebenfalls mit AtmosFringe zeichnen lassen, und jetzt faßt das Programm diesen Fehler als unterkompensiert
auf. Der HS-Linsen-Abstand muß also verkürzt werden, damit die Kompensations-Wirkung zunimmt.
10 mm Abstandsverkürzung, also 1531 mm führt aber bereits zu einer über-kompensierten Wirkung, sodaß das Optimum in der Gegend
von 1536 mm liegen müßte.
-
Schließlich setzt man diesen Abstands-Wert wieder in ZEMAX ein, und bekommt den Wert K = -1.327546
Mich würde nun interssieren, a) welchen Wert der Designer in seiner Berechnung hatte, und b) welchen Wert der Optik-Hersteller
für den HS überzeugend ausweisen kann. Wie diese Konische Konstante in das vom Designer entwickelte System paßt und wie
sich das Ergebnis in der praktischen Prüfung verhält, muß jedenfalls noch untersucht werden.
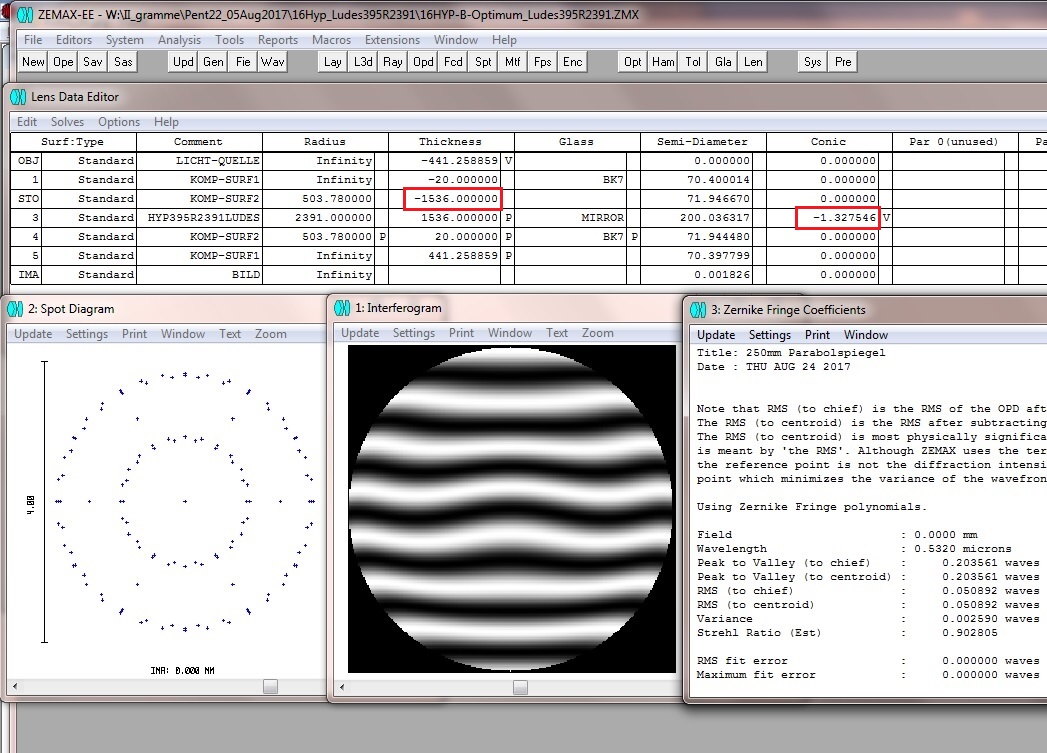
Der optimale Abstand Spiegel - Linse von 1536 mm
Der Zernike Zoo: http://r2.astro-foren.com/index.php/de/2-uncategorised/61-der-zernike-zoo-5-april-2006
Unter dem optimalen Abstand von 1536 mm Spiegel / Linse sieht man deutlich die Zone bei ca. 90% vom Durchmesser, ebenso beim Ronchi-Test
intrafokal, 13 lp/mm. 
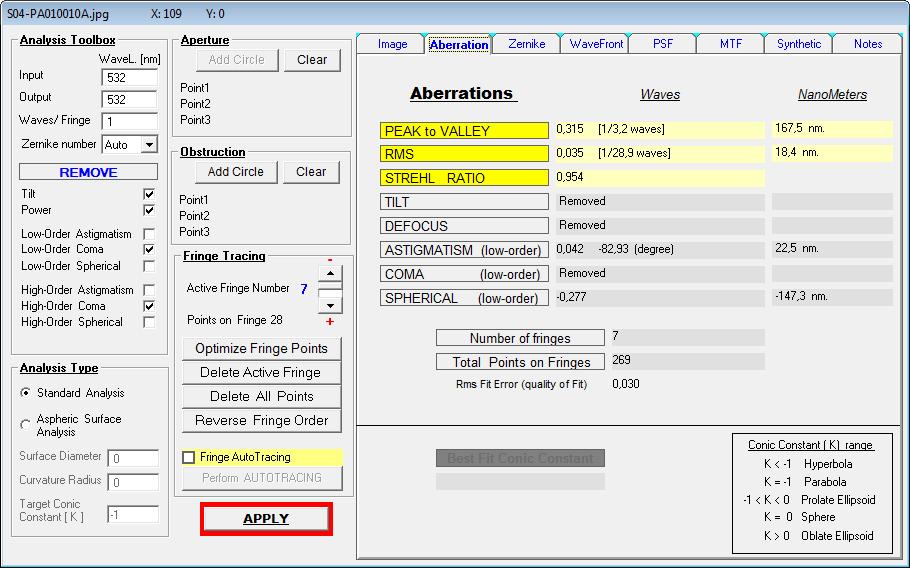
Die Auswertung von Spherical Low + high ergibt einen Strehl von 0.572, wie er in der Hauptsache über die Zone verursacht wird,
mit PV L/1.5 High Order Spherical. Da Low Order Spherical nur die Über-/Unterkorrektur darstellt, in ähnlicher Weise wie die Power,
wäre damit der richtige Abstand zwischen Linse und Spiegel mit 1536 mm erreicht. 
Und nur für Low Order Spherical gilt der Strehlwert von 0.994 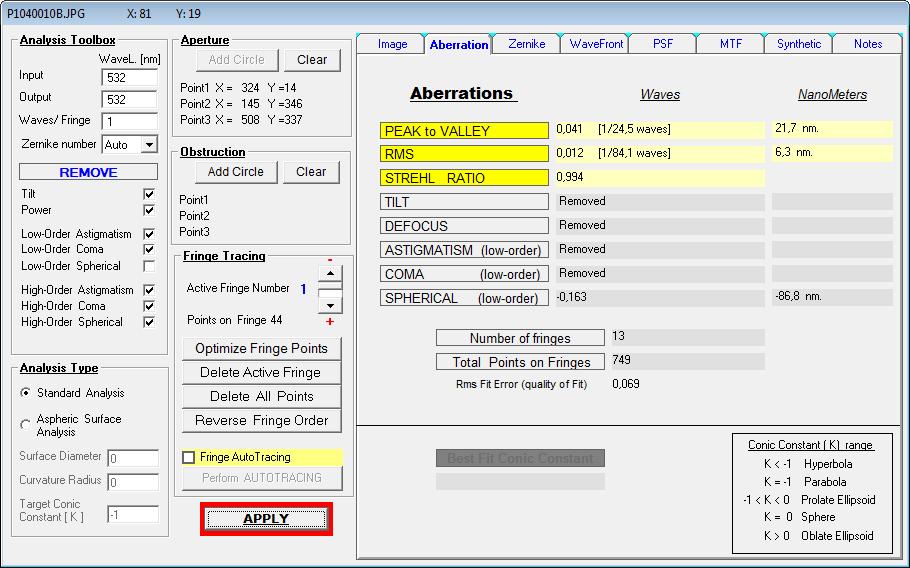
Der Unterschied zwischen Low Order Spherical im Synthetischen IGramm (links) und der Summe von Low + High Order Spherical sieht man
dagegen rechts mit dem synthetischen IGramm und einem Strehl von 0.572 . Ob allerdings diese Genauigkeit des Hauptspiegels für ein
optisches System Hyperbel + Korrektor genau genug ist, muß noch untersucht werden. 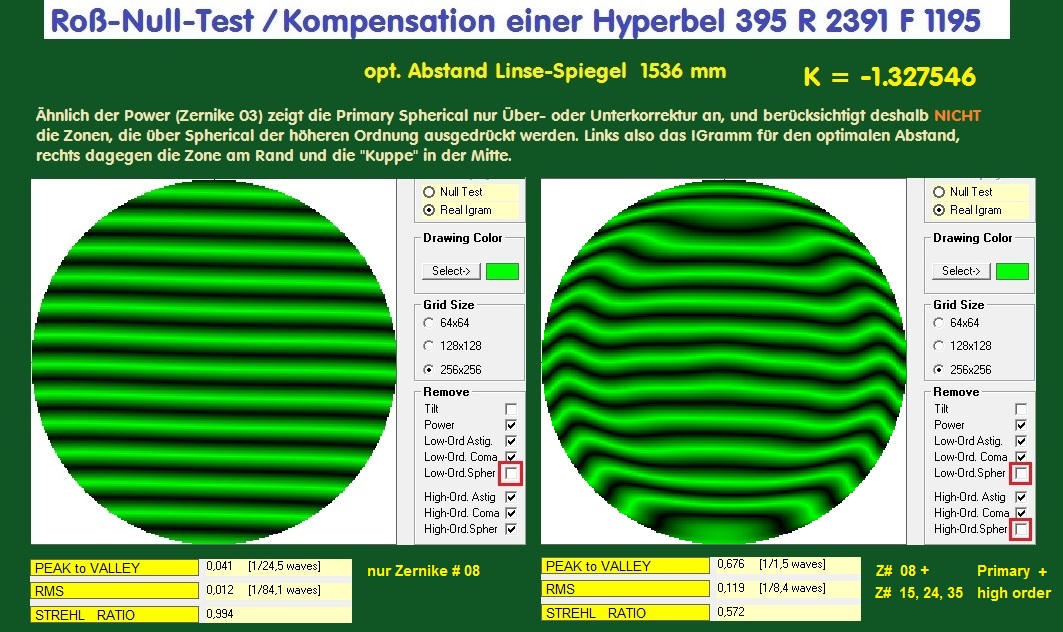
Elliptical Flat
Elliptical Flat - Frage der erforderlichen Genauigkeit
Bei der Beurteilung des elliptical Flats kann man mindestens zwei Standpunkte vertreten: Die erste Genauigkeits-Angabe bezieht sich
auf die Gesamt-Spiegelfläche. Für diesen Fall wäre der Gesamt-Strehl bei 0.758, ein vergleichsweise guter Wert über die Gesamtfläche,
wenn man nicht gerade die Gesamtfläche im Strahlengang verwenden möchte. Dann hat man eine Situation, wie bei den beiden Astro-
Kameras, die ich Anfang der 80-er Jahre gebaut habe.
C018 * Bath-Astrokamera AKI(Freiburg) und AKII(Namibia)
C019 * Bath-Astrokamera AKI und AKII Systemdaten und Bilder

Für diesen Fall braucht man nicht die Spiegel-Gesamtfläche im Strahlengang, sondern nur die Teilfläche, die der Lichtkegel jeweils im
Strahlengang tatsächlich braucht. Statt des Gesamtdurchmessers Ellipse/kleine Achse = 190 mm, wäre nur ein Kreis mit ca. 65 mm
Durchmesser (ja nach Position des Flats) zu berücksichtigen, und die Genauigkeit steigt entsprechend - letztlich eine Frage, mit welcher
Genauigkeit man die Fläche bestellt hat. 
Für die Gesamt-Fläche 190 mm wäre dann der Strehlwert 0.758 - im anderen Fall rechtes Bild mit 65 mm Durchmesser Strehl 0.980.
Da diese Newton+Korrektor-Kamera für visuelle Zwecke gebraucht wird, kann man einen solchen Wert tolerieren. 
AndereSetups
Andere Setups: Hindle-Sphere, Waineo-Test, Foucault Schnittweiten-Differenz-Messung
Die verschiedenen Setups in der Literatur:
https://www.google.de/search?q=Hindle+Sphere&tbm=isch&tbo=u&source=univ&sa=X&ved=0ahUKEwjnyazGrI7WAhUC7xQKHU21CusQsAQIMQ&biw=1622&bih=1031
http://www.telescope-optics.net/hindle_sphere_test.htm
http://www.telescope-optics.net/waineo_null_test.htm
http://www.telescope-optics.net/dall_ross_null_test.htm
In allen Fällen ist es sinnvoll, über einen anderen Test zu prüfen, ob bei einem anderen Testaufbau ähnliche bis gleiche Ergebnisse
entstehen. Man kann den HS auch über den Waineo-Test prüfen, also gegen einen Kugelspiegel. Da gibt es offenbar zwei Lösungen,
wobei die zweite Lösung sehr ungenau ist. Auch empfiehlt sich ein einfacher Foucault- oder IMeter-Test, bei dem die Schnittweiten-
Differenz zwischen Mitte ujnd Rand des HS gemessen wird.
Das folgende Setup benutzt eine Sphäre im doppelten Durchgang und kompensiert in ähnlicher Weise die Aberration der Hyperbel.
Allerdings wäre die Lichtquelle zwischen den Spiegeln, was die Messung etwas schwieriger macht. Der Vorteil ist die Herstellung der
korrigierenden Sphäre, die sich leichter prüfen läßt, als eine große Plankonvex-Linse. Sie ist dem Roß-Null-Test insofern ähnlich,
als auch hier die Sphäre im doppelten Durchgang benutzt wird. Siehe auch: http://www.telescope-optics.net/waineo_null_test.htm 
In einem anderen Setup muß der sphärische Kompensations-Spiegel eine Bohrung haben. Hier wird die Sphäre im einfachen Durchgang
verwendet, der hyperbolische Test-Spiegel jedoch im doppelten Durchgang. Der Nachteil dieser Anordnung scheint zu sein, daß die exakte
Bestimmung der Konischen Konstante bei diesem Setup "unschärfer" ist, weil der Spiegelabstand eine großere Toleranz hat und damit
die Ermittlung ungenauer wird. 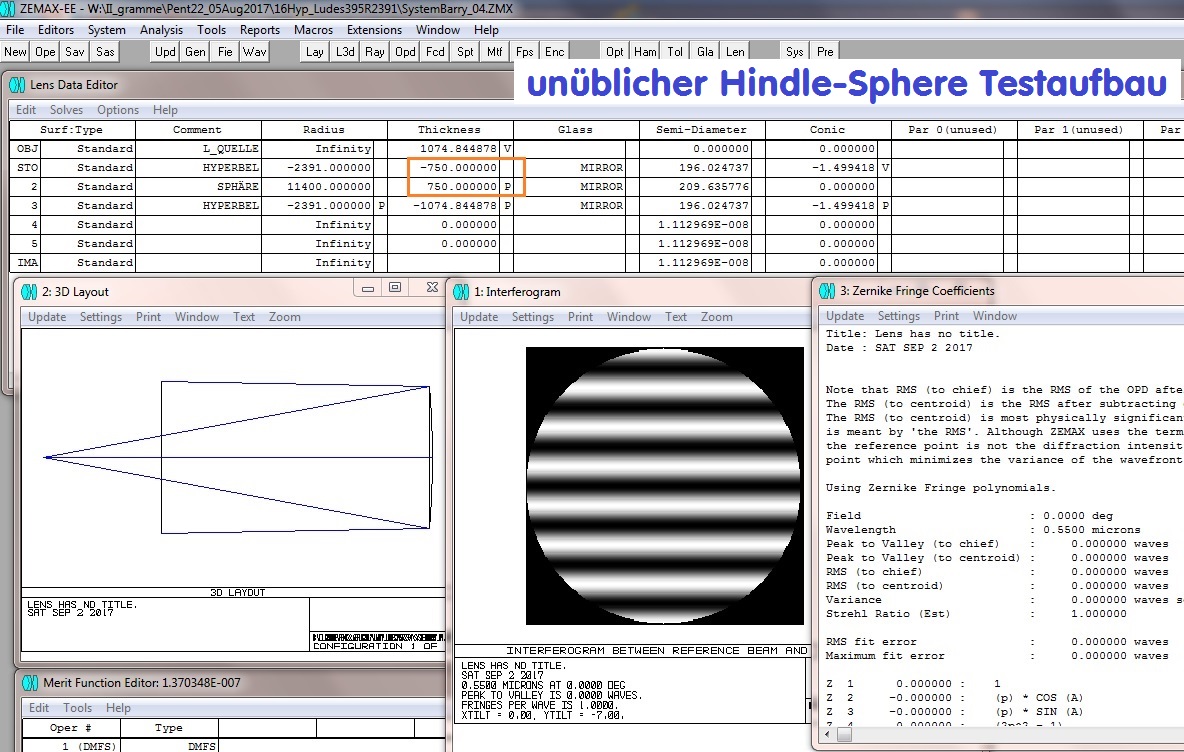
Eine Art Gegenkontrolle wäre eine Zonen-Differenz-Messung, wie man sie vom Foucault-Test kennt. Dabei reicht die Differenz zwischen
Mitte und Rand, bzw. zwischen der 0.707 und der Mitte.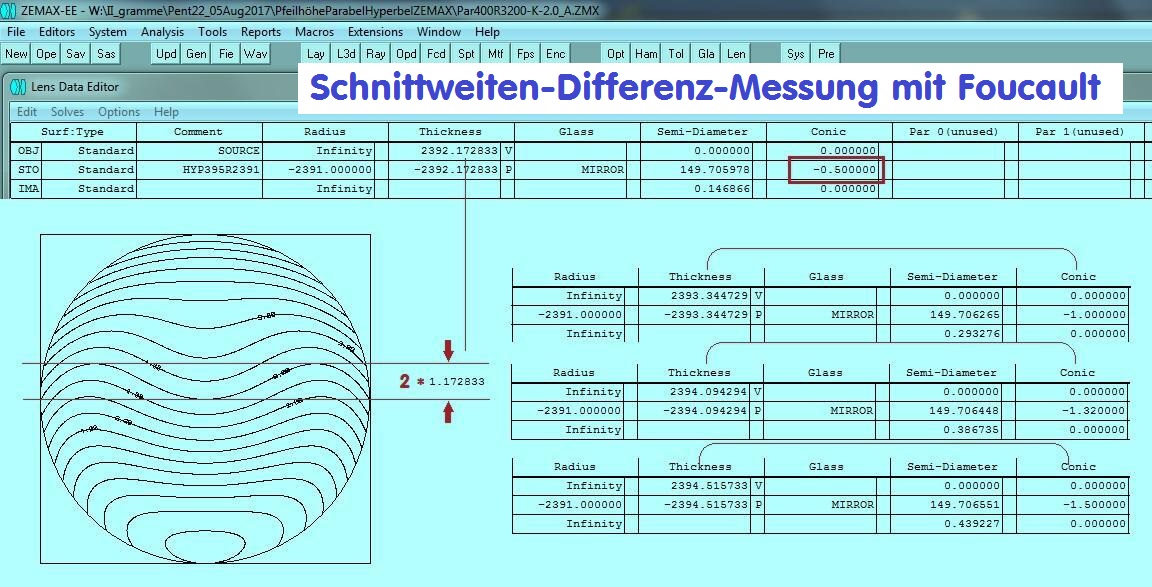
Über ZEMAX läßt sich die Schnittweiten-Differenz (Mitte-0.707-Zone-Rand) rechnen zwischen Mitte und Rand. Weil es hier die Differenz
zwischen Mitte und der 0.707-Zone ist, muß der Wert noch mit dem Faktor 2 multipliziert werden. Damit ist überprüfbar, ob die Hyperbel
tatsächlich den gerechneten Wert bzw. die erfoderliche Größe erreicht hat. Bei KoKo -1.32 wäre das dann 6. 188588 mm im Unterschied
zu KoKo -1.50 und 7.031466 mm. Dieser Unterschied wäre dann als weiteres Test-Kriterium genau genug, um die richtige Hyperbel dar-
zustellen. Statt dem Foucault-Test kann man auch einen InterferoMeter benutzen, wobei die Streifen der jeweiligen Zone waagrecht und
parallel sein muß. Mit einer 0.001 mm Meßuhr und einer Reihen-Messung wäre das hinreichend genau.
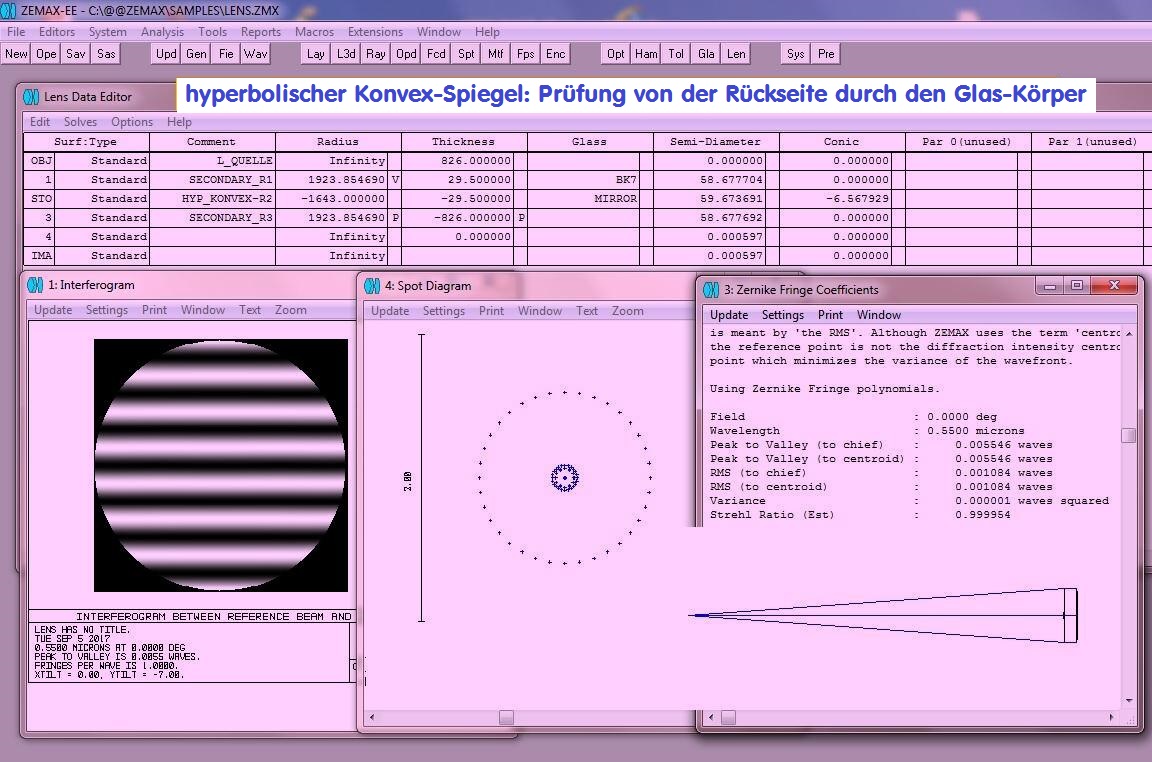
Secondary Konvex-Spiegel: Test der Hyperbel von der Rückseite durch den Glaskörper BK7 oder ähnlicher Gläser.
Für diesen Fall wird der Glaskörper als Linse verwendet. Dadurch entsteht eine Kompensations-Wirkung und man kann die Hyperbel
sehr genau auf Null prüfen.
E013C * Strehl-Fixierung, Strehl-Inflation
großes Durcheinander beim Strehlbegriff
1.http://www.astrotreff.de/topic.asp?ARCHIVE=true&TOPIC_ID=44016 Kurt'sche Verlautbarungen
2. http://forum.astronomie.de/phpapps/ubbthreads/ubbthreads.php/ubb/showthreaded/Number/241478
3. http://forum.astronomie.de/phpapps/ubbthreads/ubbthreads.php/topics/170484/Re_Glattheit_vs_Strehl
4. http://www.astrotreff.de/pop_printer_friendly.asp?ARCHIVE=true&TOPIC_ID=107920
5. http://www.astrotreff.de/pop_printer_friendly.asp?ARCHIVE=true&TOPIC_ID=142100
6. http://rohr.aiax.de/Is_that_really_your_Strehl_ratio.pdf
Fünf wahllos herausgesuchte Links zeigen, wie undefiniert bzw. unscharf selbst unter den Koryphäen schreib-aktiver Foren-User dieser
Begriff dargestellt wird: Im 3. Link findet eine Vermischung des Strehl-Begriffes mit der Flächen-Feinstruktur statt - Warum? Die
Erfassung der Wellenfront-Topografie über ein Interferogramm ist ein dermaßen grobes Raster, daß damit die Mikrorauhheit gar nicht
erfasst werden kann. Außerdem errechnet sich der Strehlwert aus dem RMS-Wert nach der Formel: 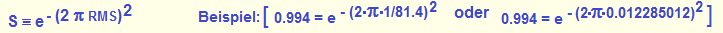
Wobei der RMS-Wert und die Mikrorauhheit sich nach Größenordnung erheblich unterscheiden würden und
am Strehlwert kaum etwas ändern können. Der entscheidende Unterschied liegt am Streulicht-Anteil, wie er durch verschieden rauhe
Spiegeloberflächen erzeugt wird. Die im 5.Link am 15.11.2012 19:53:09 Uhr veröffentlichte Formel für den Strehlwert ist falsch!
Hätte man am Testreport leicht überprüfen können!
Strehl

Aus einer etwas älteren Qualitäts-Urkunde von Carl Zeiss Jena errechnet sich die Definitions-Helligkeit (= Strehlwert) ausschließlich aus
dem RMS-Wert. Der wiederum entsteht über ein Interferogramm das die Topografie der Wellenfront darstellt. Die Interferenzlinien sind dann
die Höhenlinien der Wellenfront-Topografie und Abweichungen von der Idealform sind a) der PV-Wert und b) der über die Fläche gemittelte
RMS-Wert. Alle übrigen Erklärungen spannen eine riesige Diskussion auf, die nur in die Irre führt.

Auf die Frage (im 3. Link), ob Zit: "die Glattheit einer Spiegel-Oberfläche in den Strehlwert mit eingeht" erzählt ein ganz überzeugter
Beitrag: "Das ist keine Behauptung sondern definitiondgemäß gegeben." und beruft sich auch noch auf Suiter. Der Strehlwert basiert
auf dem Begriff der Wellenfront, im Idealfall eine Ebene aus der geometrischen Optik. Bereits hier ergibt sich ein großer Unterschied
zwischen der Wellenfront-Verformung als die größere Dimension und der Flächenrauhheit, als untergeordneter Dimension. Wer Lyot-
testbilder von Parabolspiegeln betrachtet, sieht die enorme Breite unterschiedlicher Dimensionen besonders auch im Vergleich der
sechs Spiegel.
Beschreibung des Strehl-Begriffes: 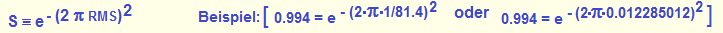
Zur Berechnung des Strehlwertes einer Optik sind folgende Schritte erforderlich:
- In einem Testaufbau (meist Autokollimation) wird zunächst ein Interferogramm/Streifenbild erzeugt, dessen Interferenzstreifen als
Höhen-Linien einer Topografie/Wellenfront aufgefaßt werden.
- Innerhalb eines Auswertprogrammes werden diese Interferenz-Linien über eine Punktlinie nachgezeichnet und
- über die ideal-typischen Zernike-Koeffizienten ausgewertet. Über den Abstand der Interferenz-Linien und über den
Abstand der Punkte verschwinden so die Strukturen, wie man sie aus der Mikrorauhheit kennt.

Alle diese Interferometer sind in Kapitel 6 ausreichend beschrieben. Siehe auch: Dave Rowe: Induced Astigmatism
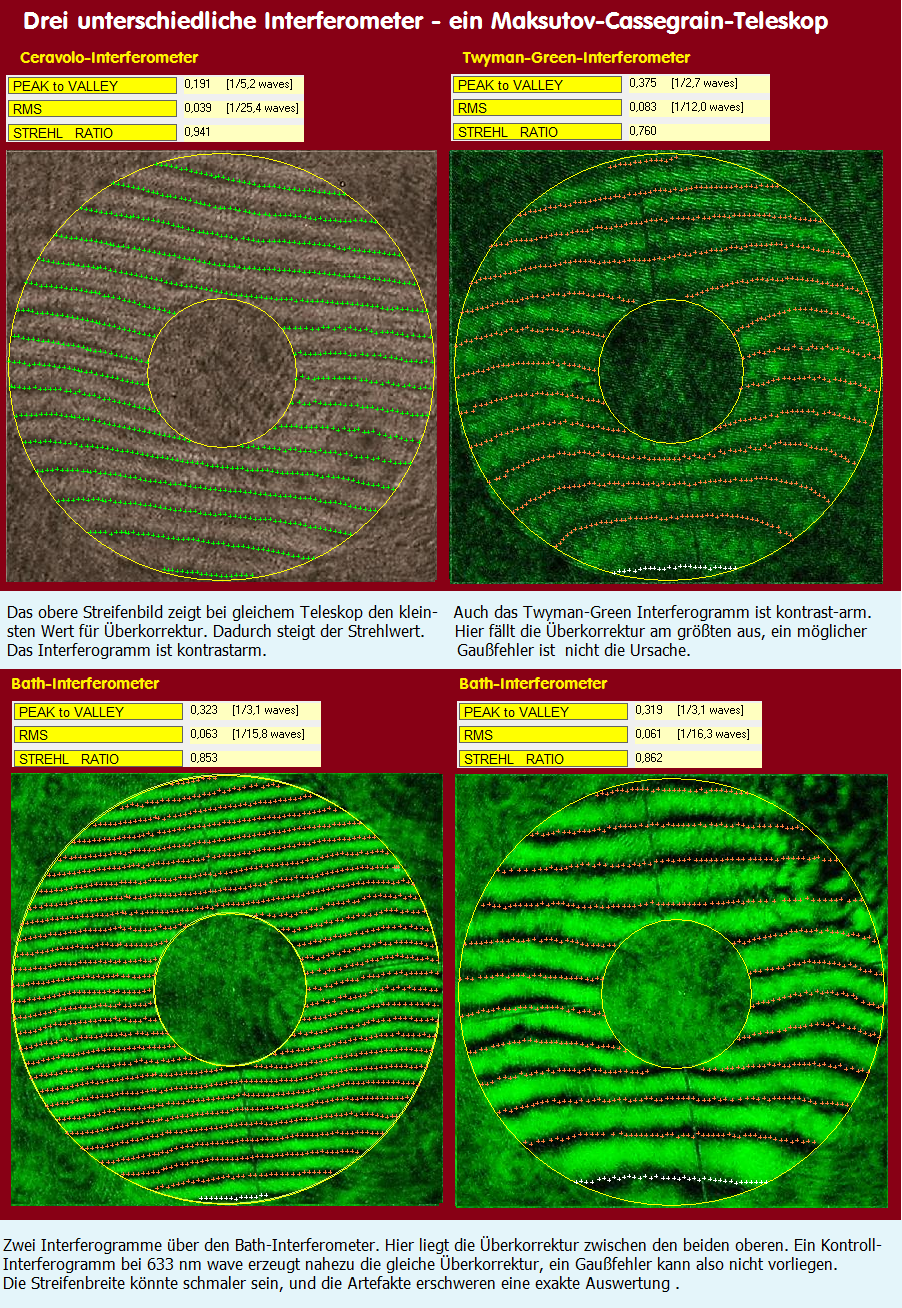
Interessanterweise streuen aber nun die Ergebnisse (z.B. Spherical) zwischen verschiedenen Interferometern, sodaß der Wunsch entsteht,
den einzelnen Interferometer in irgendeiner Weise eichen zu können. Die offenbar Interferometer-abhängigen Strehlergebnisse im nächsten
Bild zeigen deutlich, auf welch wackligen Füßen eine Strehl-Ermittlung stehen kann. Die Spherical-Differenz bei gleichem Teleskop kann
ich derzeit noch nicht erklären.
Man bezieht sich also auf eine geometrische Fläche ohne die Effekte der Mikro-Rauhheit und der Beugung. Der Strehlwert ist eine andere
Darstellungsform des RMS-Wertes und bezieht sich auf die Wellenfront-Deformation. Der Strehl-Begriff gehört in den Bereich der geometri-
schen Optik und nicht zur Wellenoptik. Im Idealfall einer perfekten Wellenfront-Ebene wäre der Strehlwert 1.000 . Dabei wird dieser Wert
üblicherweise nur auf der opt. Achse eines Systems ermittelt. Im Bildfeld - besonders bei einem fotografischen System - ist eine Strehl-
angabe nicht üblich, weshalb es dazu kaum belastbare Beispiele gibt.
Der Strehlwert errechnet sich also aus dem RMS-Wert und bezieht sich auf die Wellenfront-Deformation. Auch der RMS-Wert enthält keine
Information über die Mikrorauhheit bzw. der Beugungs-Effekte. Interferogramme einer bestimmten Wellenlänge werden als Höhenlinien
der Wellenfront-Topografie aufgefaßt und daraus unter Anwendung der Zernike Koeffizienten auf einen Strehlwert von 1.00 bis 0.0 umge-
rechnet: http://rohr.aiax.de/Strehl_K.JPG
Strehlwert bei einem Newton-Spiegel
Bei einem Newton-Spiegel hat man es mit nur einer optisch wirksamen Fläche zu tun, einem Rotations-Paraboloid. Auch hier beschreibt
der Strehlwert nur die Wellenfront-Deformation auf der opt. Achse und läßt andere optischen Eigenschaften völlig außer acht. Ein
wesentliches Merkmal, die Glätte der Fläche, die Mikrorauhheit, kann über den Strehlwert NICHT ausgedrückt werden. (Glatte Flächen
reduzieren das Streulicht und erhöhen den Bildkontrast.) (Während der Foucault- und Ronchi-Gitter-Test eine Analog-Aussage zum
Strehlwert sein können, gibt es beim Lyot-Test keine Entsprechung zum Strehl-Wert.)
Eine weitere Besonderheit bei Newton-Spiegel ist die thermische Besonderheit des Glaskörper, immer abhängig von Glasmaterial.
F098 Strehl u. Temperatur - wenn sich Spiegel durchbiegen . Durch diesen Effekt entstehen in der Beobachtungspraxis unterschied-
liche Strehlwerte, was dazu führt, daß ein perfekter Newton-Spiegel immer leicht unterkorrigiert sein sollte. Dadurch reduziert sich
der Strehlwert und relativiert den Wunsch nach einem perfekten Strehlwert von 0.99 .
Vielfach wird - als dritte Besonderheit - die Genauigkeit des ellipt. Planspiegels völlig vergessen, und auftauchende Fehler nur
beim Hauptspiegel gesucht, statt auch den Fangspiegel in die Untersuchung mit einzubeziehen. Das Kriterium "hoher Strehlwert"
für einen besonders guten Parabolspiegel muß also unbedingt differenziert bzw. relativiert werden.
Astigmatismus - Koma - Spherical
Nach der Zernike Tabelle ist der ermittelte Strehlwert die Summe dreier optische Fehler sowohl in der Grundordnung und in der
höheren Ordnung: a) der Astigmatismus, b) die Koma und c) die sphärische Aberration.
Für einen Parabolspiegel wäre nur ein signifikanter Astigmatismus der Grundordnung von Bedeutung. Trifoil- und Tetrafoil-
Astigmatismus würde man nicht sehen. Ein weiteres Argument bezieht sich auf die Größe des Rest-Astigmatismus, das ist die
Frage, ab welcher Größe man Rest-Astigmatismus überhaupt sehen würde. Noch wesentlicher ist, daß dem Parabol-Spiegel aus
schließlich der spiegel-eigene Wert zugeordnet werden darf, nicht etwa Fehlereinflüsse aus dem Testaufbau (z.B. Seeing), der
Spiegellagerung, der Hilfsoptiken oder dem Interferometer. Aus diesem Grund empfiehlt sich auch ein Zweistufen-Verfahren
bei der Auswertung von Parabol-Spiegeln. Weil der Rest-Astigmatismus den Strehlwert empfindlich nach unten ziehen kann,
ohne zu fragen, wie er zustande kommt, und wieviel davon nur dem Parabolspiegel zugeordnet werden kann, kommt diesem
ersten Testschritt - meist in RoC - besondere Bedeutung zu.
Wenn beispielsweise der Testaufbau mit einem Newton-Spiegel nicht sorgfältig zentriert worden war, zeigt sich im Interferogramm
Koma in Form von S-förmigen Linien und anderen Koma-Merkmalen. Ein Newton-System kann auf der opt. Achse keine Koma
haben, und die muß deshalb abgezogen/deaktiviert werden.
Sphärische Aberration bzw. Spherical ist immer eine Information über die Retouche eines Kugelspiegels in Richtung Parabol-
Spiegel. Ein Spiegel kann also über- oder ünterkorrigiert sein. In beiden Fällen reduziert sich der Strehlwert. Man muß also nach
dem Grund fragen, wenn der Spherical-Strehlwert-Anteil niedriger ist: Unterkorrigiert wäre weniger tragisch wie überkorrigiert.
Dazu käme die Frage nach abgesunkene Kante oder deutlich sichtbare Zonen. Die Flächenrauhheit läßt sich über den Strehlwert
leider nicht darstellen, ebensowenig die Obstruktion.
Wer also einen Newton-Spiegel leichtfertig mit dem Begriff "Gurke" belegt, beweist damit nur, daß ihm optisches Fachwissen
fehlt. Ebenso ist der Wunsch nach einem Strehl von 0.99, nur ein Beweis, daß sich der entsprechende Beitrag kaum mit opt.
Tatsachen auseinandergesetzt hat.
Anders als bei der Meßgenauigkeit im Metall-Bereich, wo 0.001 mm reproduzierbar sind, man also von Wiederholbarkeit sprechen
kann, ist ein Strehlwert auf der 3. Stellen hinter dem Komma nicht darstellbar. Selbst über die Auswertung von vielen Einzel-Inter-
ferogrammen und der Mittelung der Ergebnisse, wird das Strehl-Endergebnis nicht unbedingt genauer. Es bleibt "unscharf" auf
mindesten 1 - 2% vom Ergebnis. (Also 0.98 bis 0.99) Nicht ohne Grund geben Zertifikat einen bestimmten "Strehlwert und besser"
an in Kenntnis der Unschärfe bei der Messung. Dabei ist die Vermutung, daß ein schlechteres Ergebnis das richtigere sein müßte,
ebenso unsachlich.
Bevor man also besonders in Foren eine Optik leichtfertig nieder-schreibt, wäre ein kompetenter Blick durch ein gescholtenes
Teleskop sehr viel sinnvoller.
Der Strehlwert bei Linsen-Optiken
Bei einem Refrakator spielt die Wellenlänge der Hauptfarbe Grün mit 550 nm wave oder der e-Linie = 546.1 nm wave, oder üblicher-
weise 532 nm wave der handelsüblichen Laser-Dioden eine Rolle. Einige Optik-Designer aus der Zunft der Theorie brachten deshalb
unverzüglich den Poly-Strehl ins Spiel, ein meßtechnisch kaum zu realisierender Begriff. Man hat auch Mühe, dazu kompetente
Beispiele der bekannten Optikfirmen zu finden. E006 Der Unfug mit dem Polychromatischen Strehl. Diese Idee scheitert an den
fehlenden Beispielen, die die Meßtechnik offenbar nicht zu liefern bereit ist. Grundsätzlicher hingegen ist der farbabhängige
Öffnungsfehler, bei dem ein Objektiv im langen Spektrum (Rot) gewöhnlich unterkorrigiert und im kurzen Spektrum (Blau) über-
korrigiert reagiert, von spezifischen Ausnnahmen einmal abgesehen. Auch für diesen Bereich gilt die "Unschärfe" bei der Strehl-
auswertung. Die Unschärfe hängt auch damit zusammen, daß Interferenz-Streifen größerer Breite über Punkt-Linien nachvollzogen
werden und entweder den üblichen Artefakten zum Opfer fallen oder dem Interpretations-Spielraum der Streifenbreite, weil ein
Interferogramm leider nicht aus dünnen Linien besteht. So kann bereits ein einzelner Punkt das Strehlergebnis variieren, wenn
man ihn um 1-2 Pixel in der Höhe versetzt.
Der Strehlwert bei fotografischen Fernrohr-Systemen
Bei der Fotografie verliert der Strehlwert auf der opt. Achse völlig an Bedeutung , weil es hier um die fehlerfreie Abbildung besonders
im Bildfeld geht und der Nachweis nicht über einen Strehlwert geführt wird, sondern über eine gelungene Bildaufnahme oder
häufig über ein Spot-Diagramm aus einem Optical Design Program. Ein hoher Strehlwert auf der opt. Achse sagt über Astigmatismus
oder Koma im Bildfeld gar nichts aus. Selbst wenn ein Strehlwert über Designer Programme möglich sein sollte, findet man
aus dem Bereich der Meßtechnik kaum die entsprechenden Beispiele.
Der Strehl-Wert ein Begriff der geometrischen Optik, nicht der Wellenoptik, siehe:
https://de.wikipedia.org/wiki/Wellenoptik , https://de.wikipedia.org/wiki/Geometrische_Optik
Die Obstruktion eines optischen Teleskopes erzeugt Beugungs-Effekte, die sich über den Strehlwert NICHT darstellen lassen.
Selbst bei zunehmender Obstruktion bezieht sich der Strehlwert immer nur auf die Wellenfront-Fehler der Geometrie (also Strehl-
Wert = 1.00 im Beispiel) und nicht auf die Verlagerung der Lichtenergie in die Beuguungs-Ringe bei zunehmender Obstruktion
bei der PSF-Darstellung.
Zur Simulation, inwieweit sich Rauhheit im Strehlwert ausdrücken könnte, folgender Gedankengang, der sich ausdrücklich auf
die üblichen Streifen-Auswertprogramme bezieht, nicht auf einen Phasenshift-Interferometer und dessen computerisierte Aus-
Wertung. Aber auch dort dürfte sich die Mikrorauhheit kaum in der Reduzierung des Strehlwertes bemerkbar machen. Im simu-
lierten Beispiel wird eine Flächenrauhheit von PV L/10 angenommen und über die Wellenlinie dargestellt. PV L/10 Rauhheit wäre
ein unüblich hoher Wert.
Die Auswertung rechts reduziert den Strehlwert von ebenfalls 1.000 nicht, auch ein systhetisches Interferogramm "ignoriert"
diese Wellenlinie. Damit wäre die Behauptung, Mikrorauhheit reduziere den Strehlwert, widerlegt. 
Zur Erläuterung:
a) die rechnerische Auflösung kann nicht größer/kleiner sein, als der Abstand der Einzel-Punkte in der Punktlinie. Das gilt nur für den Höhenversatz, weil
der der Rauhheit entsprechen würde. Selbst mittlere Abweichungen, die im Interferogramm noch erkennbar wären, werden bei der Auswertung unterdrückt.
b) Auch wenn die Streifenbreite z.B. PV L/10 entsprechen würde und so eine Punkte-Verteilung über die Gesamtbreite entstünde, mittelt das Programm
auch nur eine gedachte Mittel-Linie, und stellt damit wieder nicht die Höhen-Unterschiede dar, die von der Rauhheit verursacht wird.
Siehe auch:
http://r2.astro-foren.com/index.php/de/14-beitraege/06-messtechnik-teil-2-aufbau-diverser-interferometer/695-f105a-strehl-versus-mikro-rauhheit-warum-der-strehlnur-die-wellenfront-darstellt-und-nicht-die-mikrorauhheit
http://rohr.aiax.de/StrehlSimJPG.jpg
E005 * Begriffe beim Vermessen von Optiken
Damit man grundsätzliche Fragen nicht immer neu erklären muß, hier einige Antworten
zu Fragen, die von Kunden in der AstroOptik gerne gestellt werden:
Zit: "Ein Sternfreund fragt, wie die Aussage diffraktionsbegrenzt eigentlich definiert ist."
http://de.wikipedia.org/wiki/Diffraktion_(Wasserwellen)
http://rohr.aiax.de/Beugung.jpg
https://de.wikipedia.org/wiki/Aufl%C3%B6sungsverm%C3%B6gen
https://download.e-bookshelf.de/download/0007/8467/38/L-G-0007846738-0014510208.pdf
Bei Uwe Laux, AstroOptik 2. Auflage Seite 6, findet man folgenden Eintrag:
Zit: " Definitions-Helligkeit (Deh) Wellenoptisches Bildgüte-Kriterium, ist die relative Intensität des
Punktbildes in einem Bezugspun kt (Maximum oder geometrishc-Optischer Bidlpunkt.) Sie läßt sich
über die Zernike-Koeffizienten näherungsweise berechnen (Geltungsbereich von ca. 0.6 bis 1), eine
weitere Möglichkeit ist die direkte Berechnung aus der Wellenaberration. Ein optisches System gilt
als beugungsbegrenzt, wenn { 0.8 < Deh. <= 1}
In Telescopes Eyepieces Astrographs von Gregory Hallock Smith, Roger Ceragioli, Richard Berry,
Willman Bell, Inc, 2012, Seite 81, 4.9.5 Strehl Ratio findet man dazu folgende Textstelle:
Zit:" The Strehl Ratio is a Performance metric for optical Systems that are diffraction-
limited or nearly so. It is defined as the Ratio in intensity between the central Peak of the theore-
tically perfect Airy disk (or the associated point spread function) and the Peak produced by an
aberrated optical System. Expressed as a percentage , a Strehl Ratio of 100% indicates a perfect
optical System. By convention, any System that produces a Strehl Ratio of 80% or higher
is considered diffraction limited."
Bei Otterstedt http://www.otterstedt.de/wiki/index.php/Beugungsbegrenzt findet man:
Zit:" Das heisst, ein System gilt als beugungsbegrenzt, wenn seine Definitionshelligkeit (Strehlzahl)
mindestens einen Wert von 0,8 erreicht oder anders ausgedrückt die Helligkeit des zentralen Beugungs-
scheibchens mindesten 80% des theoretisch möglichen Wertes erreicht.
(Näheres zu Passfehlern und speziell der genauen Definition dess Begriffs Beugungsbegrenzt ist in DIN ISO 10110-5 (Optik und
optische Instrumente - Erstellung von Zeichnungen für optische Elemente und Systeme - Teil 5.)
Bei Newton-Spiegel streiten sich besonders die praktischen, visuellen Beobachter, die einen Qualitäts-
Unterschied erkennen wollen zwischen Strehl = 0.80 und Strehl 0.99. Für die Astro-Foto-grafie spielen
diese Unterschiede eine untergeordnete Rolle. Auch bei einem Refraktor überlagern andere Merkmale
die Aussage "beugungsbegrenzt". (Siehe unten Fußnote *)
Zit: "Wavefront Error, Peak-to-Valley RMS, Strehl. Und ob nur eine spezielle Wellenlänge verwendet wird?
Wenn ein Newton-Spiegel mit einem Interferogramm beworben wird - unabhängig über welchen Test-
Aufbau bzw. mit welchem Interferometer das Interferogramm erstellt worden ist - dann wird dieses
Interferogramm mit seinen Interferenz-Streifen wie die Höhen-Linien einer Landkarte aufgefaßt und
stellt einen quantiativen Test dar. Bereits mit bloßen Auge erkennt man aus diesem Streifenbild sowohl
Astigmatismus und sphärische Aberration in Form von Über- oder Unterkorrektur. Koma darf man bei
der Vermessen von Parabolspiegeln abziehen, weil die Parabel auf der opt. Achse keine Koma haben
kann, sodaß die Koma aus dem Testaufbau stammen muß. Auch beim Astigmatismus muß man bei
der Zuordnung sehr vorsichtig sein: Er kann über die Lagerung von Prüfspiegel, von Kollimations-
Planspiegel und schließlich über das "Seeing" des Testaufbaues eingeführt werden. Es gilt nur der
Astigmatismus, der vom Prüfspiegel selbst eingeführt wird. (Siehe unten Fußnote **)
Das Interferogramm, auch als Streifenbild bezeichnet, wird über die Zernike-Koeffizienten ausgewertet. @ Der Zernike Zoo
Bei einem Interferogramm muß immer die Wellenlänge angebenen sein, in der es erstellt worden ist.
Das ist besonders bei einem Refraktor wichtig, wegen des farbabhängigen Öffnungsfehlers (Gauß-Fehler)
Dabei werden zwei Werte ermittelt:
a) der Peak to Valley Wert mit höchster Erhebung (Peak) und tiefster Stelle (Valley)
b) der RMS-Wert in der Optik, (Root Mean Square), ist ein auf die Gesamtfläche gemittelter PV-Wert.
Ein PV-Fehler am Rande eines Spiegels beansprucht eine größere Fläche als ein PV-Fehler in der Mitte.
Der RMS-Wert und der Strehl-Wert sind nur unterschiedliche Darstellungs-Weisen und können deshalb
wechseltseitig umgerechnet werden.
Strehl-Begriffinfo1, info2, info3, info 4, praxis-ferne Strehl-Diskussion/Einflußgrößen, @immer wieder Strehl Rauhheit, Transmission, Reflektivität
Die Strehlermittlung über ein Interferogramm wird von vielen Störquellen begleitet, sodaß
man immer von einer Unschärfe von bis zu +/- 1%-Punkte des Strehlwertes ausgehen muß.
Das führt bei vielen Zertifikaten zur Bemerkung, daß der angegebene Strehlwert einen Mindest-
Wert darstellt und die Optik deshalb auch besser sein kann.
Bei vielen Optiken ist der Strehlwert nur ein Qualitäts-Kriterium, wird aber leider in der Szene
von den sog. "Strehlis" regelrecht verabsolutiert, weil sie nur dieses Qualitäts-Kriterium kennen.
Fußnote *)
Ein besserer Beweis für die "Beugungs-Grenze" bzw. das Auflösungs-Vermögen einer Optik ist die Auflösungs-
Formel, die sich an der Eintritts-Öffnung (Durchmesser) und der Wellenlänge einer Optik orientiert:
Auflösung arcsec (bei 550 nm wave) = 1.22*Lambda*206265 / Eintritts-Öffnung (für Lambda 550 nm wave)
Auflösung arcsec für 550 nm wave = 138.4038 / Eintritts-Öffnung. Siehe auch: http://rohr.aiax.de/Gross_Physik_III_Kap_7.pdf
Der durch Rechnung entstandene Wert in BogenSekunden (arcsec) kann über das Auflösungs-Vermögen eines Fotos über die bekannten Abstände
eines engen Doppelsternes meines Artificial Sky Testes über den inv. Tan aus Abstand/Fokus ermittelt werden und stimmt in den meisten Fällen mit
dem theoretischen Auflösungsvermögen überein.
Der Stern- / Artificial Sky Test - Sammung und Übersicht von Beiträgen
Fußnote **)
Auch beim Thema Astigmatismus ist zu fragen, ab welcher Größe er visuell wahrgenommen werden kann. Bei hohen Vergrößerungen etwa ab PV L/4. Damit entsteht
eine weitere Unschärfe hinsichtlich eines exakten Strehlwertes: Man würde einen Astigmatismus in der Größe von beispielsweise PV L/6 zwar nicht wahrnehmen, aber
meßtechnisch würde dieser den Strehlwert um einige Prozent-Punkte drücken, mit der Folge, daß eine sonst perfekte Optik nur aus diesem Grund als schlechter ein-
geschätzt würde. Insofern muß man den Strehlwert differenzieren in seine Teilfehler und deren anteilige Größe. Bei der Fotografie wird Astigmatismus über die
längere Belichtungszeit über das Seeing "verschmiert", ist also ebenfalls auf dem Foto nicht erkennbar. In der Regel ist die opt. Genauigkeit eines Systems um ca. den
Faktor 3 genauer, als es die Pixel des Kamera-Aufnahme-Chips überhaupt darstellen können.
E045B Besondere Anforderungen an einen 16-inch Referenz-Kugelspiegel - große Planflächen testen 31.12.2016
Im Archiv: W:\II_gramme\Pent21_12Dez2016\16SphereFelberR3096Rand46\TestMitAloisFlat
Hier geht es zum unteren Kommentar:
Planflächen kann man prinzipiell gegen eine Sphäre prüfen. Deshalb sollte die Sphäre eine besondere Genauigkeit haben. Im Foucault-
Test erwartet man einen "topf-ebenen" Flächeneindruck. Die opt. Fläche sollte möglichst keine erkennbaren Zonen haben und keinen
deutlich abfallenden Rand. Der Astigmatismus des Kugelspiegels sollte möglichst klein sein und die Flächenrauhheit im Lyot-Test einen
möglichst glatten Eindruck hinterlassen. Die Fläche des Kugelspiegels ist mit 1/3 im Gesamtergebnis der jeweiligen Testbilder vertreten
- aber man möchte ja Planflächen beurteilen und weniger die Fehler der Referenz-Sphäre. Den ersten derartigen Versuch, eine solche
perfekte Sphäre zu bekommen, startete ich vor 11 Jahren. Offenbar gelang es mir damals nicht, dem damaligen Spiegelschleifer meine
Wünsche zu vermitteln. Es kam deshalb nach dieser Aktion zu einem folgenschweren Zerwürfnis zwischen dem Schleifkünstler und mir,
dessen Ego sich über diesen Vorgang heftig beleidigt fühlte. Nach zehn Jahren startete ich ein weiteres Mal einen erneuten Versuch bei
einem Spiegelschleifer meines Vertrauens, und dessen Ergebnis soll in diesem Bericht dargestellt werden.
Die Einflüsse von "Luftunruhe" und Spiegel-Lagerung
Die Prüfung einer Referenz-Sphäre beginnt mit der vertikalen Lagerung des Glaskörpers, der offenbar in unterschiedlichen Positionen
auch unterschiedlich in sich "zusammen-fällt". Das ist ein Effekt des Glaskörpers in senkrechter Position und hat zunächst nichts
mit der unterschiedlichen Art der Lagerung zu tun. Das kann, wie auf dem Foto zu sehen, eine Lagerung in einem 40 mm breiten Gurt_
band sein, oder wie im übernächsten Bild unten zu sehen . . .

-
die Lagerung auf zwei Wippen, die von unten im Winkel von 90° zum Zentrum der Glasscheibe angeordnet sind. Diese
Form der Lagerung ist sofort "stabil" und schließt andere Bewegungen aus, wie langsames "Einhängen" in das Gurtband.
Dieser Effekt führt zu Beginn zur Veränderung der Spiegel-Position, bis sich alle mechanischen Einflüsse stabilisiert haben.

-
Genau die folgende Prüfung hat mit dem Spiegel-eigenen Rest-Astigmatismus zu tun und der muß sorgfältig unterschieden
werden von einem Astigmatismus, der über die Lagerung des Glaskörpers entsteht. Die Überprüfung aus dem Krümmungs-
Mittelpunkt der Sphäre mit den folgenden Interferogrammen ist eine solche Möglichkeit. Aber bereits hier begegnet man dem
nächsten meßtechnischen Problem - die Luftunruhe, indem unkontrollierbare Schlieren über das Interferogramm "hinwegziehen".
Der Testaufbau bekommt in der Folge eine "Einhausung", also ein Tunnel aus Styropor-Platten zur Beruhigung der Luft-
Schwaden. Man müßte sich einen eigenen Raum zulegen, bei dem es keine Luftströme mehr gibt. Die Heizung einzuschalten
ist für diesen Zweck streng verboten. Aus diesem Grund hat der Spiegelschleifer meines Vertrauens seinen Arbeitsraum
im tiefsten Keller unter der Erde. Als Test-Ergebnis sollten dann derartige konzentrische Interferenz-Ringe entstehen, die
einen möglichen Rest-Astigmatismus dokumentieren.
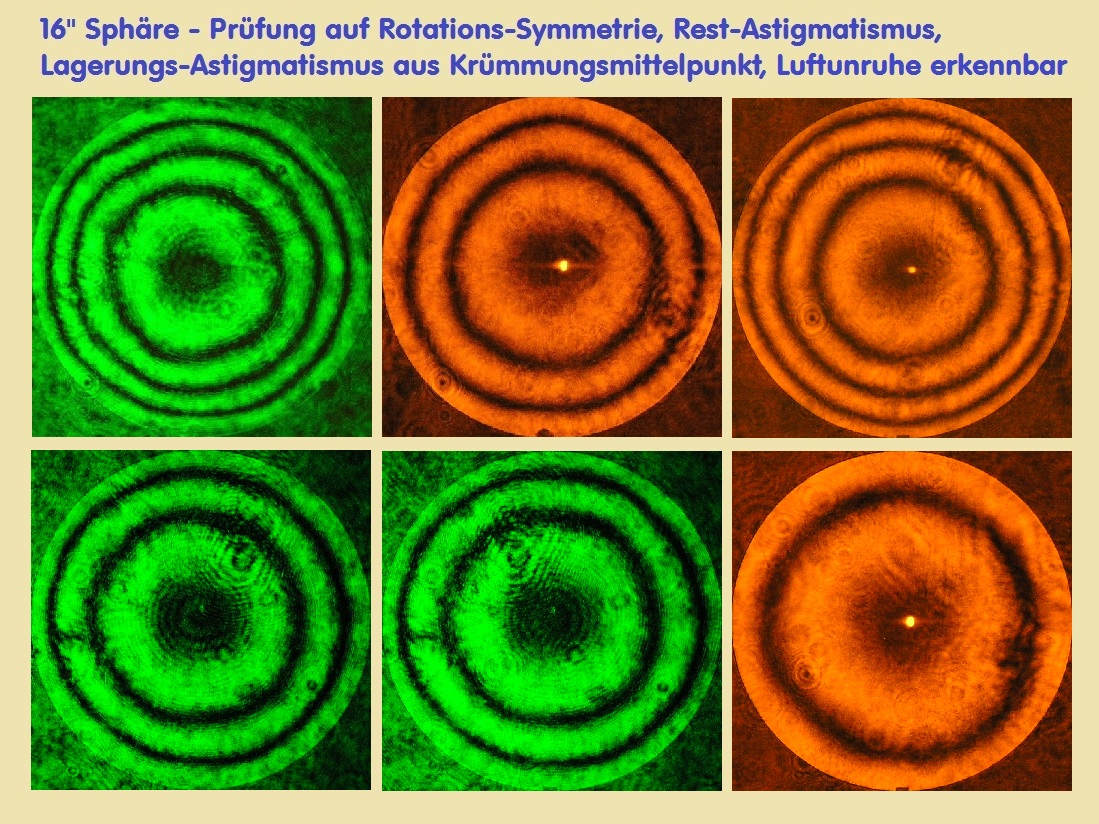
-
Diese Interferenz-Ringe lassen sich Strehl-mäßig auswerten, Koma und Spherical werden deaktiviert. Als Ergebnis liefert
das Programm nur den Wert vom Rest-Astigmatismus. Dazu reicht es völlig, wenn dieser Wert ca. PV L/10 über die gesamte
400 mm Kugel-Fläche beträgt, da man in der Regel Planflächen mit kleineren Durchmesser prüft. Größere Planspiegel
könnte man natürlich über dieses Verfahren ebenfalls prüfen.
-
-
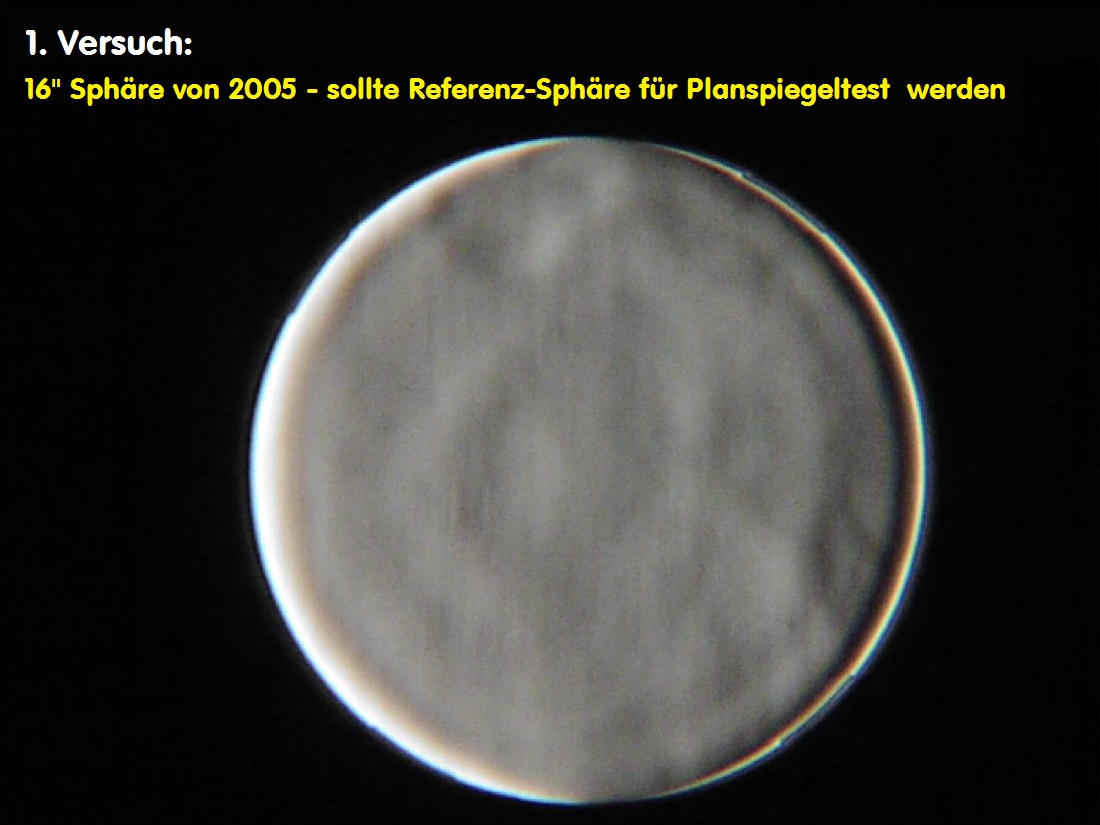
Der 1. Versuch vor 11 Jahren - Im Ordner w:/.../400-Sphaere-.../
In der Spiegelschleifer-Szene gibt es ab und zu gute Handwerker, wie Zambuto, David Verneth, Alluna-Optics, Intes, LOMO und
andere und eine Reihe sogenannter Primadonnas, die sofort tödlich beleidigt reagieren, wenn man nur die leistesten Zweifel an
ihrer Schleifkunst verlauten läßt. An einen solchen Zeitgenossen bin ich unglücklicherweise beim ersten Mal geraten und ich
konnte ihm leider nicht vermitteln, daß ich an einen Referenz-Spiegel zur Prüfung von Planflächen besondere Ansprüche stelle.
Das hat auch damit zu tun, weil Planflächen in der Regel eine wesentlich glattere Oberfläche haben und man dann statt der
Planfläche in Wirklichkeit die Fläche der Sphäre betrachtet. Der damalige Kugelspiegel war zwar nicht schlecht, nur für eine
Referenz-Sphäre hatte ich mir mehr erhofft. Nachfolgend die Ergebnisse des damaligen Experiments. Bei flüchtiger Betrachtung
könnte man das folgende Bild für Schlieren-verrauscht halten, wie der Kommentator unten im Kommentar meint. Dann sieht er
aber nicht die Zonen, die diese Sphäre in der Mitte und am Rand hat. Und das war diesem Schleifkünstler leider nicht nahe zu
bringen. Es macht schon einen Unterschied, ob man über ein langjähriges Erfahrungswissen eines Feinoptikers verfügt, oder
nur die Foren vollschreibt.
-
Bereits vor 11 Jahren war es sinnvoll, den spiegel-eigenen Rest-Astigmatismus von der Sphärischen Aberration zu trennen, um die
Einflüsse aus dem Testaufbau selbst zu reduzieren. Das folgende konzentrische Interferogramm entsteht deshalb immer im Krüm-
mungsmittelpunkt, weil dann die Fehlereinflüsse überschaubarer sind, also unbeeinflußt von weiteren opt. Komponenten. Also nur
noch Lagerung, Luftbewegung und Raumschwingungen etc. (Der Scale-Faktor ist 1.)
-
Die Anzahl der Streifen auf dem Ronchi-Bild sollten nur 2 - 3 Streifen sein, damit man die Beugungs-Linien und deren
Zwischenräume besser sieht, weil man damit eine Information über die Glätte der Fläche bekommt.

-
Ganz perfekt ist die Fläche leider nicht. Neben einer abgesunkenen Kante läßt sich in der Mitte eine flache Kuppe erkennen. Für
einen Parabolspiegel wäre das schon lange perfekt, nur als Referenz-Sphäre möchte man die Fläche besser haben, und darin
bestand der unüberbrückbare Dissens. Es ist also schon ein Unterschied, ob man als Feinoptiker über 40 Jahre hochwertige Optiken
hergestellt hat, oder als selbsternannter Schleifkünstler nur sein Ego pflegt.
-Der Wellenfront zufolge ist auch am Rand eine leichte Zone.
-
Für einen Parabolspiegel wäre das ein glänzendes Ergebnis, weil auch die thermische Bewegung einkalkuliert wäre. Nur für eine
Referenz-Fläche waren meine Ansprüche leider etwas höher - sorry.
-
Der 2. Versuch im Jahr 2016
Daß die Herstellung eines perfekten Kugelspiegels eine hohe Kunst ist, braucht man mir nicht zu erklären. Eine 400 mm Polierschale
ist nahezu unberechenbar, schon mal abhängig von der Geschwindigkeit, mit der man poliert. Und wenn es dann noch eine Referenz-
sphäre sein soll, schaut man noch kritischer auf die Fläche selbst. Ganze 11 Jahre dauerte es, bis ich einen neuen Versuch startete,
ich sollte nämlich einen größeren Planspiegel prüfen. (Zum Thema Flächenglätte gibt es das bereits in den 50-er Jahren von Hans Rohr
veröffentlichte Buch "Das Fernrohr für Jedermann" mit eindrucksvollen Beispielen)

-
Bereits das Ronchi-Testbild ist ein Hinweis, daß man eine glatte Fläche vor sich hat: Wenn die weißen, breiten Streifen gleich-
mäßig und ungestört zu sehen sind, wenn die schmalen Beugungslinie dazwischen im dunklen Bereich gut sichtbare Linien sind,
und wenn die dunkle Fläche dazwischen weitestgehend dunkel und ungestört abgebildet ist, dann ist die Gesamtfläche ziemlich
glatt. Das Gegenbeispiel einer rauhen Oberfläche bilden die GSO Spiegel, die maschinell in hohen Stückzahlen hergestellt werden.
Besonders glatte Spiegel bekommt man bei Zambuto oder früher bei David Vernet in Frankreich.

-
Bei 1700-facher Vergrößerung, wie der folgende Artificial Sky Test zeigt, würde man sofort sowohl Astigmatismus und sphärische
Aberration erkennen. Bei einem perfekten Kugelspiegel muß dieser Test zu einer perfekten Abbildung führen, wenn denn die
Luftbewegung erfolgreich ausgeschaltet worden ist. Die Dreiergruppe in der Bildmitte bestätigt fotografisch das theoretische Auf-
lösungsvermögung von ca. 0.3 arcsec. 
-
Dieses Interferogramm bei 587.6 nm wave entstand schließlich, nachdem die Einflüsse von Lagerung und Luftunruhe weitest-
gehend ausgemerzt worden waren - zugleich ein deutlicher Hinweis, wie unscharf Messungen sein können, wenn man die Fehler-
Einflüsse aus dem Testaufbau zu wenig beachtet.

-
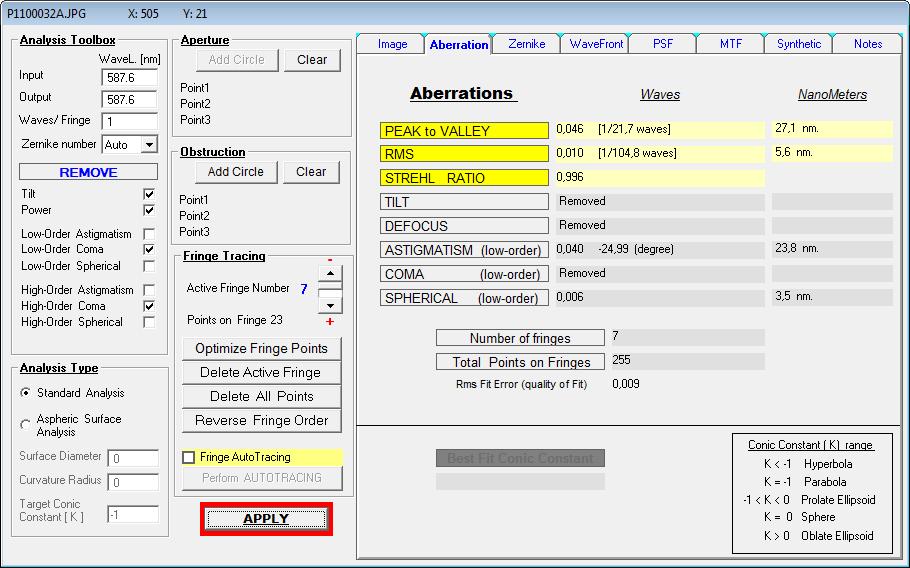
Diese Wellenfront-Darstellung entspricht einem Gesamt-Fehler von PV L/21.7 und muß deshalb nicht genauer sein.
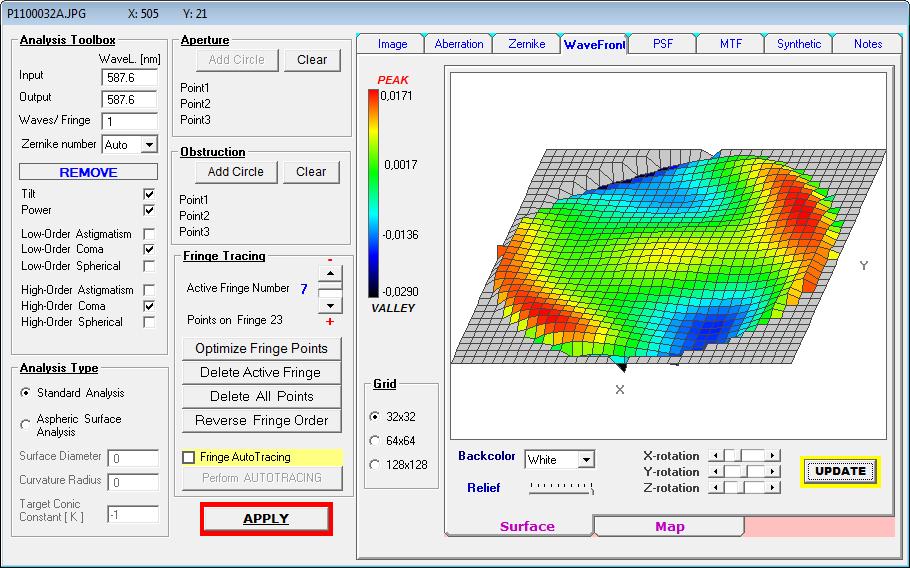
-
Ganz allgemein läßt sich sagen, daß eher selten Plan-Spiegel mit Durchmesser 400 mm gegen die Sphäre geprüft werden.
Entsprechend genauer ist dann die Referenz-Kugelfläche bei kleineren Planspiegel-Durchmessern.
-
Im nächsten Schritt wird man die Tauglichkeit dieser Sphäre untersuchen, wenn damit Planspiegel geprüft werden. Auch für den
Spiegelschleifer ein wichtiger Aspekt.
Test eines 400-er Flat gegen die Sphäre
Die übliche Aufstellung: Der Planspiegel steht im 45° Winkel zur Sphäre, ähnlich wie bei einem Newton-System.
Im Aufbau sieht man einen leichten Höhenversatz der beiden Spiegel zueinander, auch müßten die Spiegel etwas
näher zusammen-gerückt werden. Für einen prinzipiellen Test jedoch ausreichend. Während die Lagerung der
Sphäre überprüft wurde, dürfte die Lagerung des Planspiegel noch optimierbar sein. Hier wird der Planspiegel
jedoch im doppelten Durchgang gemessen - als Referenzspiegel jedoch immer nur im einfachen Durchgang.

Im Vergleich zur Sphäre hat der 400-er Flat im Zentrum zur Bohrung hin einen Flächenabfall von ca. PV L/14, mittig in der Fläche
noch eine flache und "weiche" Rinne die man im Interferogramm nicht mehr sieht, aber mit dem Foucault-Test. Die Planspiegel-
fläche wäre damit genau genug. Entscheidend ist die Regelmäßigkeit der Planspiegel-Fläche, gegen die später gemessen wird. 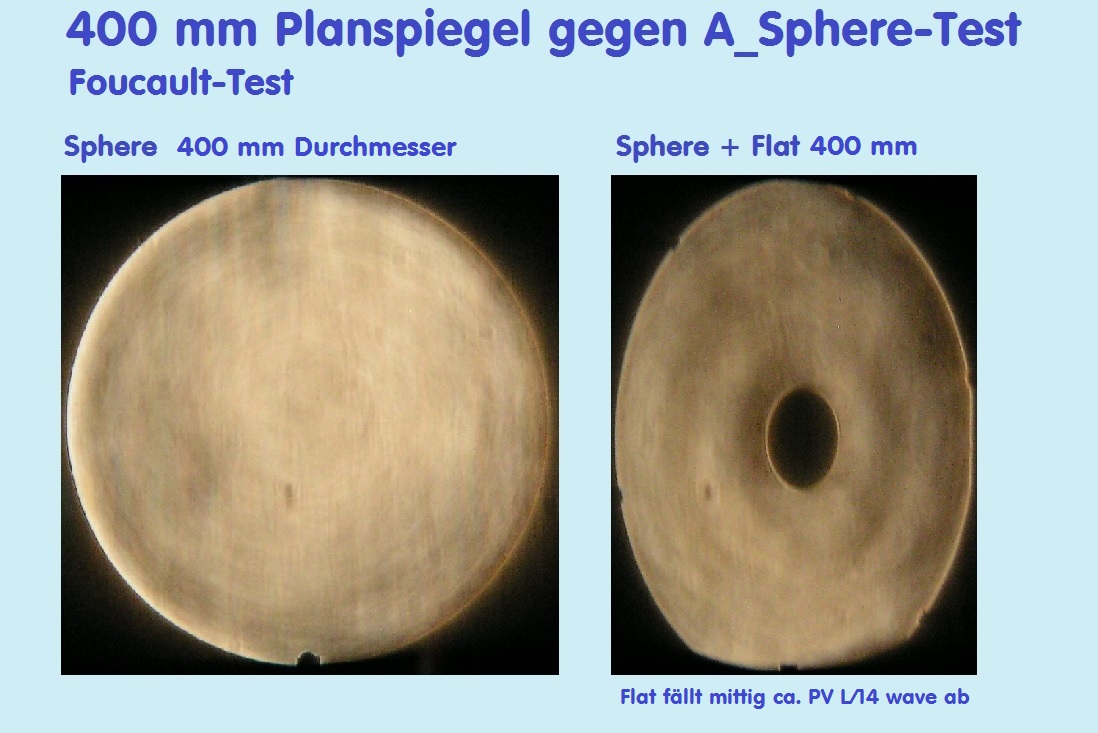

Die Ronchi-Bilder im Vergleich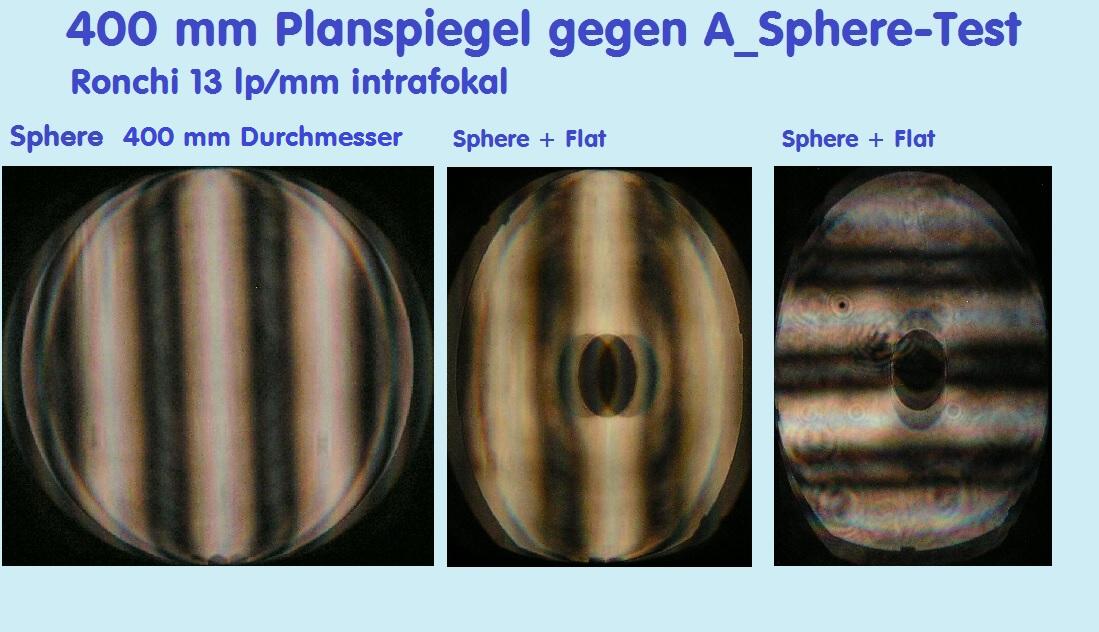
Die urspüngliche ovale I_Gramm-Ellipse wird in Y zu einem Kreis verkürzt und dann ist sie mit AtmosFringe auswertbar.
Auch in diesem Fall wird nur die Regelmäßigkeit = Spherical untersucht, weil gegen sie die Korrektur der Parabel geprüft
werden kann. Selbst die Power des Planspiegels muß nicht perfekt sein, weil ja in Total-Reflexion geprüft wird. 
Für diesen Fall ist ein Wert von PV L/14 ausreichend, der sich ausschließlich auf die Regelmäßigkeit bezieht. Diese Test-
anordnung bezieht sich auf den vollen Durchmesser des Planspiegels, bei kleineren Planspiegel wird von der Sphäre
weniger an Fläche gebraucht, somit wird auch die Messung noch genauer. Für diesen Fall kann ich einen 210 mm Plan-
Spiegel benutzen.
220 mm Zeiss-Planspiegel gegen 400 mm Sphäre
Abhängig vom Durchmesser des Planspiegels wird ein unterschiedlich großer Durchmesser der 400 mm Sphäre benutzt. Je nach Winkel,
den beide Spiegel zueinander haben, entsteht eine mehr oder weniger ausgeprägte vertikale Ellipse. Will man ein möglichst kreisförmiges
Test-Bild erzielen, dann muß der Abstand der Spiegel zueinander etwas größer sein, da der Kugelspiegel den Planspiegel sonst verdecken
würde. Auch ist der Lichtkegel unterschiedlich: Für den Kugelspiegel allein wäre das R/7.7 (bei einen Parabolspiegel f/3.8, weil der Radius
immer das doppelte vom Fokus ist.) Beim Test vom 210 mm Zeiss-Flat entsteht jedoch ein Lichtkegel von ca. R/14.7, was wiederum
bedeutet, daß die dafür nötige Kugel-Referenz-Fläche entsprechend kleiner sein muß. Auch verlangt ein R/14.7 Lichtkegel eine entspre-
chend längere Belichtungszeit, das erzielte Bild fällt nicht mehr so "brilliant" aus, wie man nachfolgend bei den Bildern sehen kann.
Bei diesem Testaufbau ging es darum, die Verzerrung aus der Perspektive möglichst klein zu halten und damit ein eher kreisförmiges
Gesamt-Bild.
-
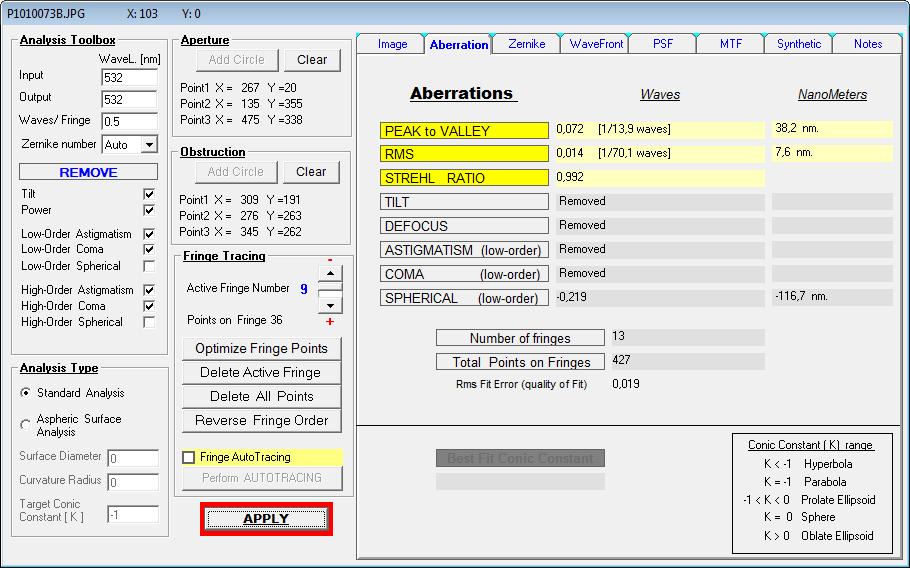
Die Mulde im rechten Bildteil muß also dem Zeiss-Planspiegel zugeordnet werden und hätte eine Größe von PV L/25 wave, also viel
genauer, als erforderlich, aber im Foucault-Test gut zu sehen, bei dem man PV L/40 immer noch gut sehen würde, so die Auskunft eines
erfahrenen Fein-Optikers. 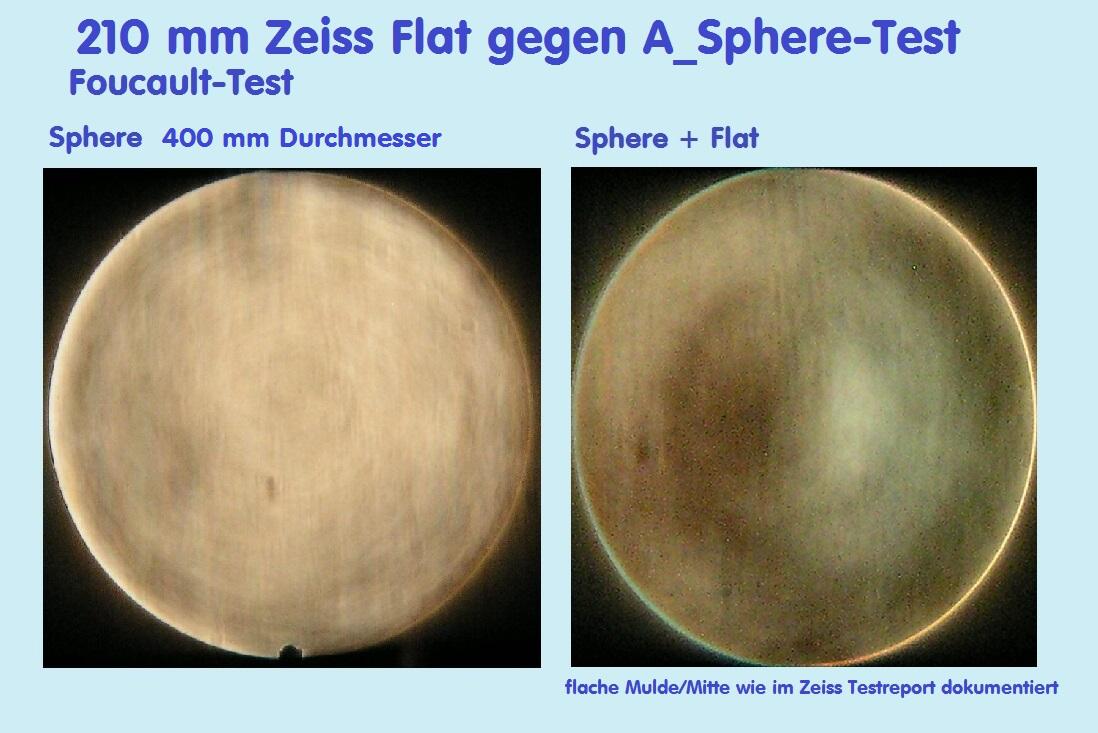
-
Der Ronchi-Test bildet die "Mulde" von PV L/25 wave in der Mitte ebenfall gut ab im rechten Bildteil. 
-
Die Wellenfront-Darstellung nur bezogen auf die sphärische Aberration bzw. der Regelmäßigkeit 
-
Die Wellenfront über den Gesamt-Testaufbau incl. Astigmatismus, bei dem aber nicht klar ist, wieviel dem Planspiegel zugerechnet
werden muß. 
Das damalige Testbild von Zeiss, das unten 0.033 wave ausweist bei vermutlich 632.8 nm . Die Ergebnisse (siehe das dritte folgende
Bild) liegen nicht weit voneinander entfernt. 
Das synthetische Interferogramm bei 532 nm wave gegen den Kugelspiegel erzeugt. 
-
Und schließlich die sphärische Aberration bzw. die Regelmäßigkeit von knapp PV L/25 wave. 
Würde man den Astigmatismus aus dem Testaufbau ebenfalls zulassen, dann liegt das Gesamt-Ergebnis immer noch bei PV L/10.
Was aber nicht bedeutet, daß man den Astigmatismus von PV L/10 ausschließlich dem Planspiegel zuordnen könnte.
Man stößt in diesem Fall an die Grenzen der Auswertung selbst - man sollte die Ergebnisse deshalb nicht verabsolutieren.
Im Autokollimations-Setup testet man also in jedem Fall gegen einen PV L/10 Planspiegel (bezogen auf den vollen Durchmesser)
und besser, auch deswegen, weil man nie den vollen Durchmesser der Planfläche braucht.

Auswertung des ursprünglichen Zeiss-Interferogrammes bei vermutlich 632.8 nm/Spherical
Zu diesem Zweck wurde das Bild zunächst invertiert, damit AtmosFringe die dunklen Streifen als Interferenz-Linien erfasst. 
Der über das obere IGramm ermittelte PV-Wert von 0.030W liegt in der Nähe des ursprünglichen Zeiss-Wertes von 0.033 W.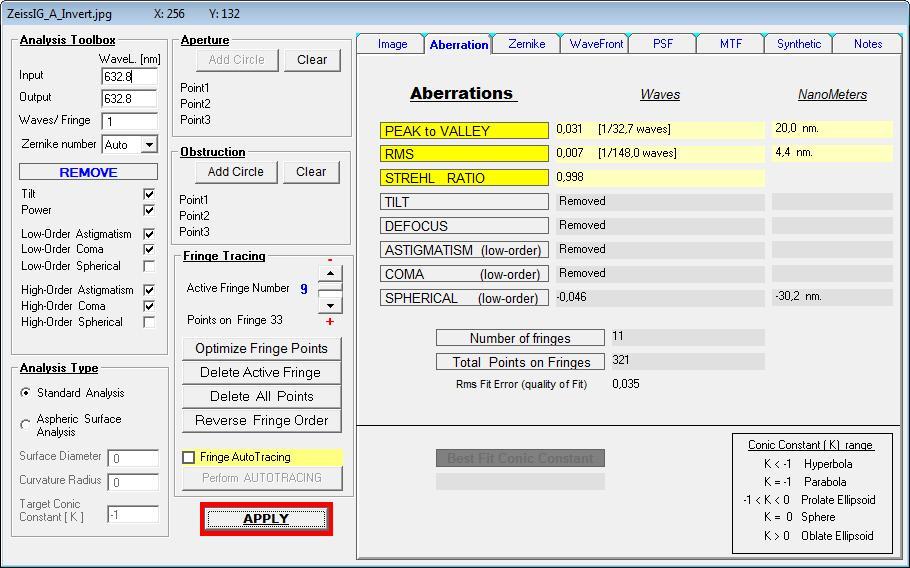
Auch beide Wellenfront-Darstellungen zeigen die "Mulde" im Zentrum . . .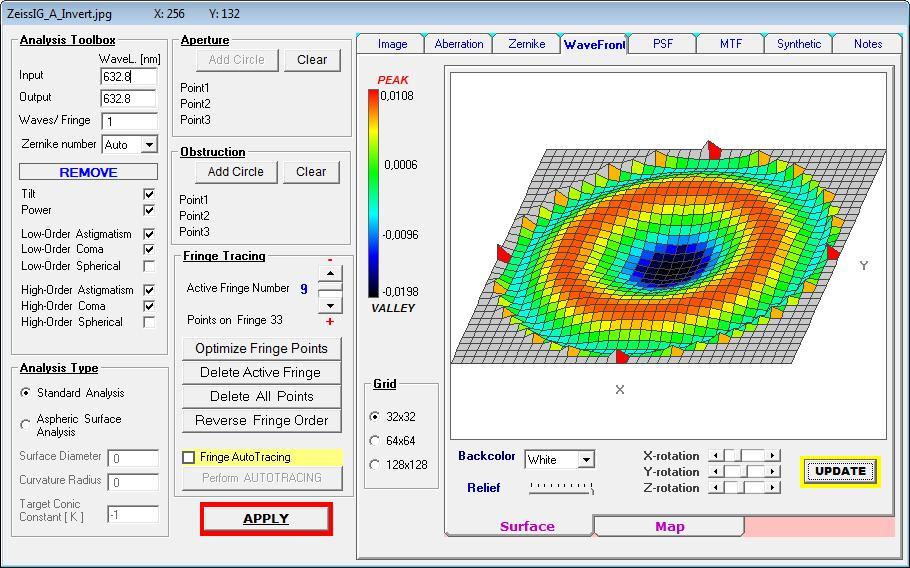
und dazu die ursprünglichen Zeiss-Darstellung.
Anders als bei Hohlspiegeln kann man die Fläche bei Planspiegeln zunächst nicht mit dem Foucault-Test untersuchen. Dieser Test
zeigt bis weit über PV L/40 vorhandene Flächenunregelmäßigkeiten. Mit einer perfekten Sphäre ist hingegen der Foucault-Test bei
Planflächen wieder möglich und zeigt auch minimale Restfehler. Als Kollimations-Planspiegel sind die oben beschriebenen Spiegel
trotzdem hinreichend genau.
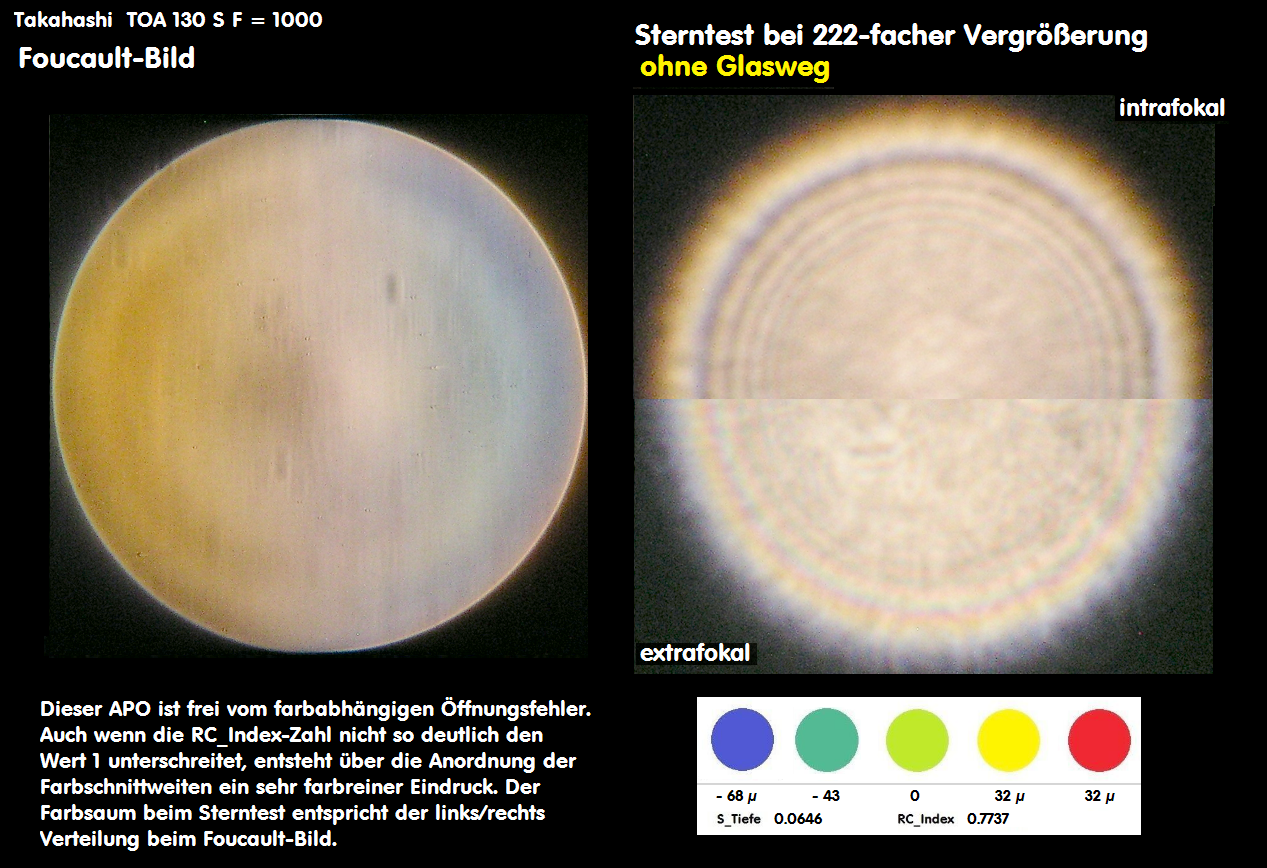
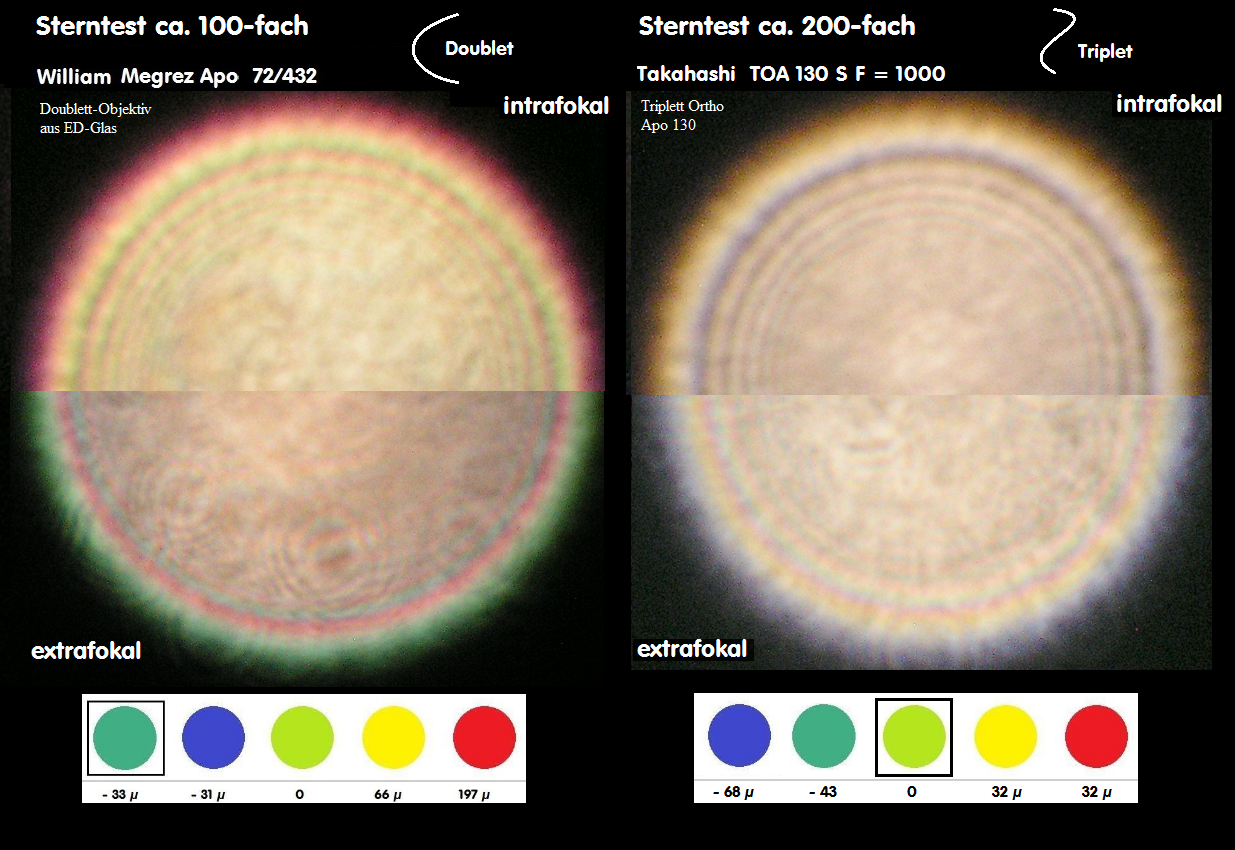
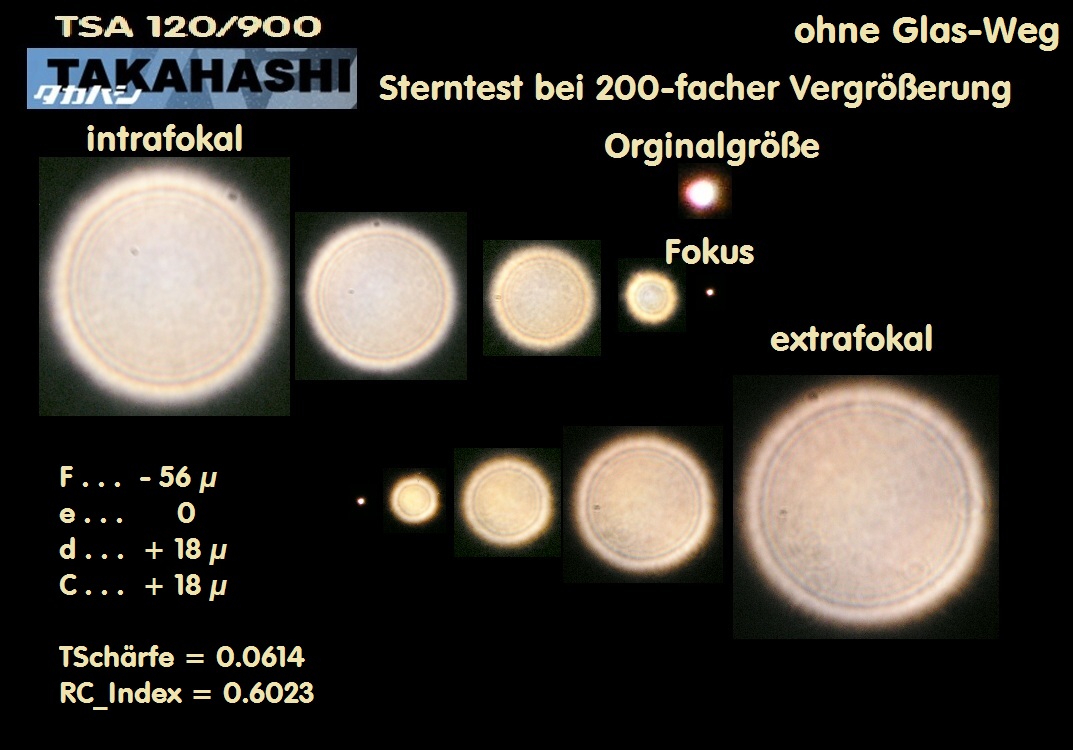
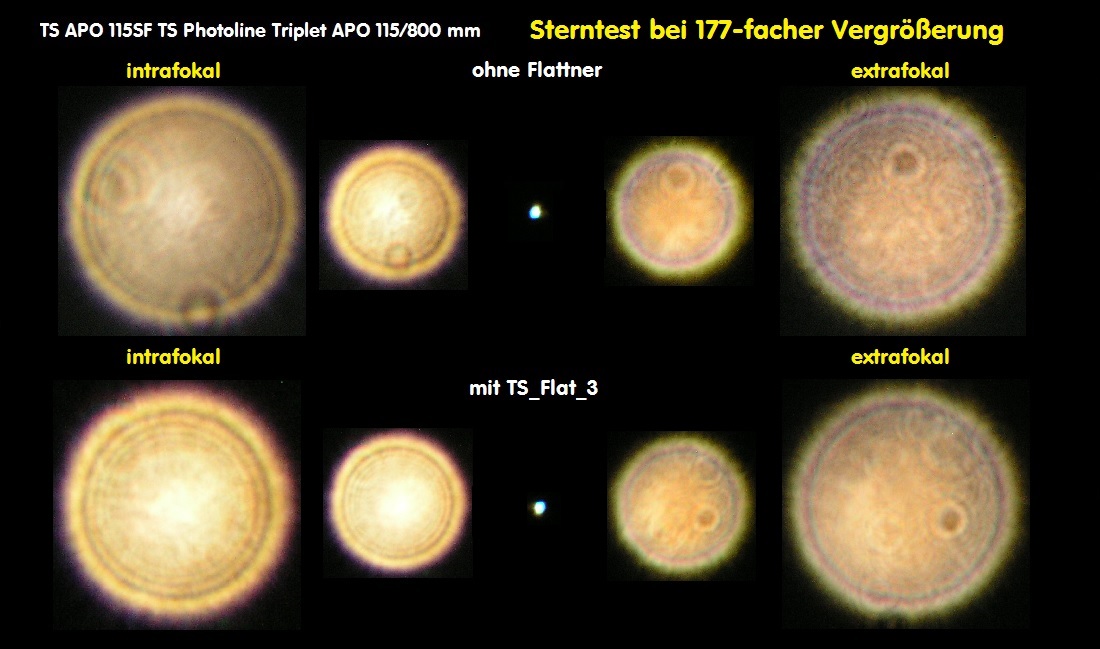
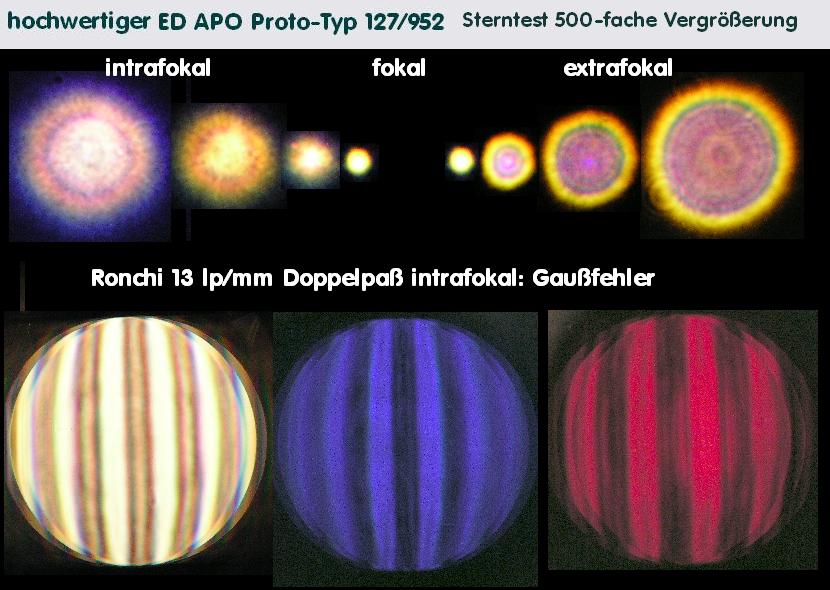
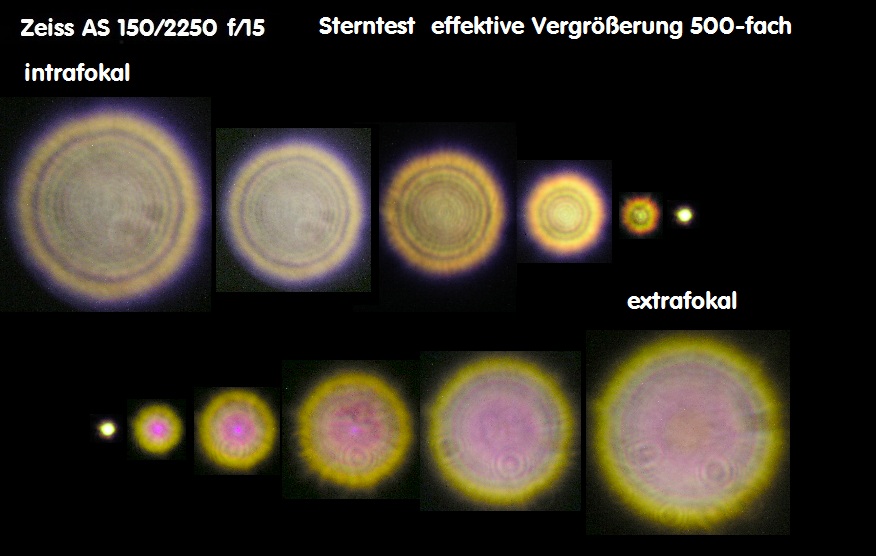
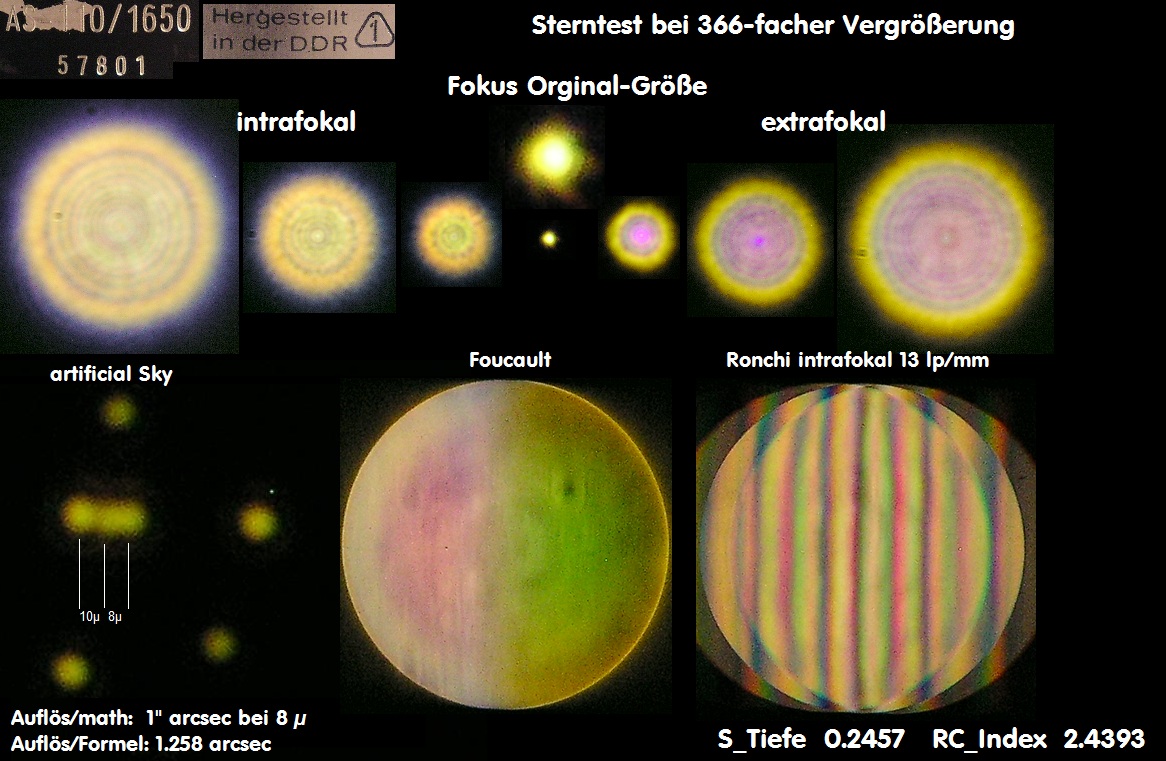
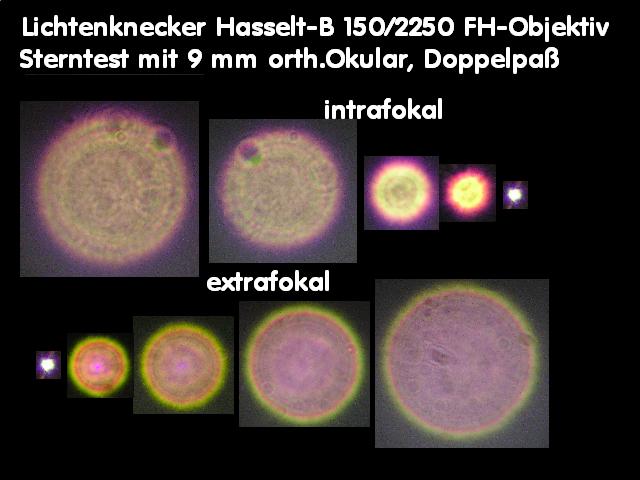
E059A * Sterntest - bei Refraktoren, Merkmale, Farbreinheit
E006A Von der Unmöglichkeit den PolyStrehl meßtechnisch korrekt darzustellen
Vorbemerkung: Während die RC_Index-Zahl eine universelle Vergleichszahl für das Sekundäres Spektrum aller Refraktoren darstellt,
versucht die Polystrehl-Diskussion den Gaußfehler für einen kleinen Bereich zu reklamieren und einzubinden:
Während bei Linsen-Systemen das Sekundäre Spektrum auf Basis realer Messungen als Verhältniszahl ermittelt wird und damit universell
vergleichbar ist, führt die Einbindung des Gaußfehlers über den Strehlwert/Diagramm zu keiner sinnvollen Vergleichbarkeit von Linsen-Optiken:
Vom Design-Programm kommt der gerechnete Wunsch, von der Meßtechnik die gemessenen Wirklichkeit. Nicht ohne Grund taucht bei
Test-Reports auf Basis von Interferogrammen niemals ein PolyStrehl-Diagramm auf. Lediglich über Design-Programme erstellte Schaubilder
sollen fiktiv Teleskop-Objektive in idealisierter Form bewerben. Üblich ist hingegen ein Test-Report als Qualitäts-Nachweis für ein aktuelles
Teleskop mit einer Serien-Nummer. Weil manchen Hobby-Designer die Praxis-Erfahrung aus der Fertigung fehlt, überziehen sie einige Foren
mit unausgegorenen Vorschlägen.
Ein Polystrehl-Diagramm ist das idealisierte Ergebnis aus einem Optical Design Programm
Die Hauptfarbe bzw. das beste Strehlergebnis sollte im grünen Spektrum bei 550 nm oder der e-Linie liegen
Das Farbspektrum liegt z.B. beim TSA zwischen 422.5 nm und 677.5 nm , Norm-Werte dazu gibt es nicht.
die Meßpunkte auf der Gesamt-Skala haben einen Abstand von 25.5 nm mit differenzierter Gewichtung.
Fertigungsfehler wie Koma und Astigmatismus fehlen, der Gaußfehler bei Grün ist nahezu Null
Die Strehl-Berechnung kann a) vom Fokuspunkt-Grün aus gerechnet oder aber b) auf jeden einzelnen Meßpunkt bezogen sein.
Im Zusammenhang damit sind die idealisierten Spot-Diagramme auch nur die gerechnete Theorie, nicht die aktuelle Wirklichkeit
Die Berechnung und Darstellung durch den Computer ist eine Sache von Sekunden
das gefertigte Objektiv ist immer nur eine Näherung an das idealisierte Polystrehl-Diagramm ; Link01, Link02, Link03,
Der Polystrehl kann meß-technisch am individuell gefertigen Objektiv nicht überzeugend dargestellt werden.
Ein individuell gefertigtes Objektiv wäre nur im Rahmen der Streubreite repräsentativ und unterscheidet sich von einer "Design"-Darstellung
Das Optimum hinsichtlich bester Strehlwert bzw. Gaußfehler=Null schwankt zwischen Blau und Rot und kann nachträglich korrigiert werden
Fertigungs-Fehler, Astigmatismus, Koma und Spherical (teilweise) müßten zu Vergleichszwecken generell/teilweise abgezogen werden
Die Meßpunkte auf der Gesamt-Skala im Farbspektrum sind nicht definiert, werden oft willkürlich gewählt
Die Bandbreite der verwendeten Interferenz-Filter ist ebenfalls undefiniert, eine Gewichtung ist nicht festgelegt
Nicht festgelegt ist, ob der Polystrehl-Wert vom Fokuspunkt Grün aus ermittelt wird, oder isoliert über jeden spektralen Meßpunkt.
Bei Test-Reports namhafter Hersteller sucht man meßtechnische Polystrehl-Diagramme vergebens --- macht keiner
Die Vermessung und Berechnung ist eine Sache von Stunden - eine nutzlose Fleißarbeit mit geringem Informationswert.
.

Ein paar Beispiele, wie fragwürdig so ein Versuch sein kann:
Beispiel 01 - B028
Das Optimum dieses individuellen Borg ED liegt im blauen Spektrum. Dort ist der Strehlwert am höchsten, der Gaußfehler geht gegen Null.
Nun sollte aber das Optimum im grünen Spektrum liegen, also entweder bei 550 nm wave oder bei der e-Linie 546.1 nm wave.
Damit eignet sich dieser Fall bereits nicht mehr hinsichtlich Gaußfehler-Vergleich. Man müßte also den Abstand der beiden Linsen
verkleinern, damit sich das Optimum in das grüne Spektrum verschiebt, damit Blau leicht über- und Rot leicht unterkorrigiert reagiert.
Es liegt also über dem System eine Unterkorrektur die dazu führt, daß sich die Überkorrektur bei Blau kompensiert und bei Rot entspre-
chend verstärkt. Es gibt sicher Gründe für diese Korrektur-Situation, nur zur meßtechnischen PolyStrehl-Darstellung taugt dieser Fall nicht.
Beispiel 02 - B032A
Bei diesem Beispiel spielt dasÖffnungsverhältnis von F/20 eine große Rolle. Der Gaußfehler spielt weder bei Blau noch bei Rot eine signifikante
Rolle, sondern nur der Farblängsfehler. Eine PolyStrehl-Darstellung wäre also unsinnig, sodaß der Vergleich der Strehlwerte zu keiner sinnvollen
Information führt. Eine PolyStrehl-Darstellung über meßtechnische Ergebnisse kann in vielerlei Hinsicht angezweifelt werden, also eine nutzlose
Aktion ohne Informations-Wert und sie beschreibt das aktuelle Objektiv nicht.
Beispiel 03 - B034
http://r2.astro-foren.com/index.php/de/10-beitraege/02-ed-optiken-halb-apos-und-frauenhofer-systeme/556-b034-meade-ed-halb-apo-127-1140-die-kunst-des-klebens
Hier müßten die Fertigungs-Fehler abgezogen werden, besonders der Zonen/Öffnungsfehler, der über dem System liegt. Wie isoliert
man deshalb den Fertigungsfehler im Bereich der sphärischer Aberration vom Gaußfehler. Auch hier ist eine meßtechnische PolyStrehl-
Darstellung kaum exakt durchzuführen und ohne weiteren Informations-Wert.

Beispiel 04 - B062
Bei diesem Fall liegt das Optimum im roten Spektrum und man müßte erst den Linsenabstand vergrößern, wenn das Optimum im grünen
Spektrum (=Hauptfarbe) liegen soll. Es ist ein F/10 FH und der Gaußfehler wäre nicht signifikant im Vergleich zum Farblängsfehler und
der RC_IndexZahl von 4.5. Hier müßte man Astigmatismus und Koma deaktivieren, damit man überhaupt mit anderen FH's vergleichen
kann. Auch hier ist der Informations-Wert gering.
Wer also die Polystrehl-Darstellung mit Hilfe der Meßtechnik fordert, ist sich nicht bewußt, mit welchen Schwierigkeiten er es zu tun bekommt.
Beispiel 05 - A044
Auch hier ist in der Hauptfarbe Grün nicht das Optimum, also der Gaußfehler = 0. Spherical Error setzt sich also aus der leichten Unterkorrektur
zusammen zusammen mit dem Gaußfehler, der hier Null sein sollte. Eine meßtechnische Polystrehl-Darstellung ist erneut nicht ganz "scharf".
Da aber das Öffnungsverhältnis mit F6 sehr groß ist, fällt hier der Gaußfehler entsprechend größer aus.
Beispiel 06 - A046
Zum einen liegt das Optimum im blauen Spektrum, zum anderen liegt über dem System ein Öffnungsfehler, der mit dem Gaußfehler
konkurriert. Man hat also Probleme, Öffnungsfehler und Gaußfehler meßtechnisch richtig zu differenzieren.
Beispiel 07 - A059
Im folgenden Beispiel liegt das Optimum des äußerst farbreinen Beispiels im roten Spektrum, wie man bereits am Ronchigramm gut beweisen
kann. Demzufolge reagiert das kürzere Spektrum überkorrigiert. Der Gaußfehler mischt sich deshalb auch mit dem Zonenfehler und ist deshalb
kaum zu isolieren: Ein meßtechnischer PolyStrehl wird auch für diesen Fall kaum möglich sein.
Beispiel 08 - A060
http://r2.astro-foren.com/index.php/de/9-beitraege/01-aeltere-berichte-auf-rohr-aiax-de-alles-ueber-apos/124-a060-tmb-apo-nr-354-lzos-115-805-hochwertige-optik
Eine PolyStrehl-Kurve verbietet sich, da in diesem Fall lediglich lediglich bei fünf Meßpunkte mit Interferenzfiltern von einer Bandbreite von 10 nm
Interferogramme erstellt wurden. Bei diesem äußerst farbreinen Objektiv wurde der Gaußfehler in Strehlwerten/Spherical angegeben, weil er in
der Hauptfarbe nahezu bei Null war und noch am ehesten eine meßtechnische Aussage zuließ.
Aber auch dieses Beispiel eignet sich kaum zu einem vergleichbaren Beispiel. Aber die Streuung selbst bei hochwertigen Objektiven kann es
gut zeigen und ist auch in diesem Fall nicht mit der idealisierten Poystrehl-Darstellung aus einem Design-Programm vergleichbar. So wenig
Spotdiagramme die meßtechnische Wirklichkeit darstellen können, hat auch die Polystrehl-Darstellung in der Meßtechnik nichts verloren.
Bild auf neuer Seite, oder Bild unten anklicken. 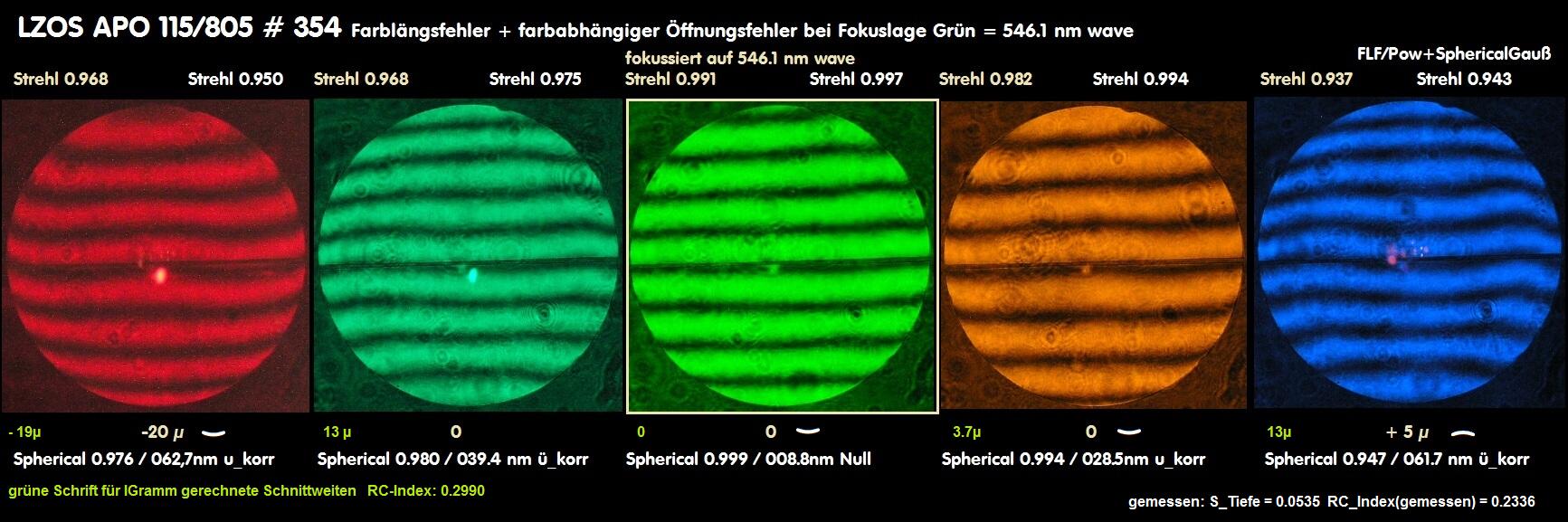
E006B PolyStrehlBegriff ---- der Unterschied zwischen Theorie und Praxis
Begriff RC_Indexzahl
Meine RC_Indexzahl ist eine zahlenmäßige Darstellung des unteren Längs-Aberrations-Diagrammes in der 0.707 Zone im Verhältnis
zur wellenoptischen Abbildungs-Tiefe. Weil sich meßtechnisch die Fokus-Differenz von F- und C-Linie zur Hauptfarbe e-Linie
problemlos messen läßt über Interferogramme oder andere Testverfahren, ist die so erhaltene Rest-Chromasie-Index-Zahl
eine universelle Darstellung aller Linsen-Objektive zum Begriff der Längen-Aberration. Der in diesem Zusammenhang
diskutierte Gaußfehler=farbabhängige Öffnungsfehler als zusätzliches Unterscheidungs-Kriterium, spielt lediglich in einem kleineren
Bereich zwischen Halb-APO und APO eine nicht genau bestimmte Bedeutung. Hier wird nun bezeichenderweise von einem
Designer der Poly-Strehl-Begriff in die Diskussion gebracht und mit der RC_Indexzahl begrifflich vermischt.
Begriff Poly-Strehl
Ein Polystrehl-Diagramm ist das Produkt eines Optical-Design-Programmes und stellt die idealisierte Form einer Optik dar.
Es ist also nicht das Ergebnis eines meßtechnischen Vorganges, weil in diesem Zusammengang wesentliche Grundbegriffe
nicht geklärt worden sind:
Das Polystrehl-Diagramm ist das idealisierte Ergebnis aus einem Optical Design Programm
Die Haupt- oder Bezugs-Farbe sollte im grünen Spektrum bei 550 nm oder der e-Linie liegen
Das Farbspektrum liegt z.B. beim TSA zwischen 422.5 nm und 677.5 nm
die Meßpunkte auf der Gesamt-Skala haben einen Abstand von 25.5 nm mit differenzierter Gewichtung.
Fertigungsfehler wie Koma und Astigmatismus fehlen, der Gaußfehler bei Grün ist nahezu Null
Die Strehl-Berechnung kann vom a) Fokuspunkt Grün aus gerechnet oder aber b) auf jeden einzelnen Meßpunkt bezogen sein.
Im Zusammenhang damit sind die idealisierten Spot-Diagramme auch nur die gerechnete Theorie, nicht die aktuelle Wirklichkeit
Die Berechnung und Darstellung über das Design-Programm ist eine Sache von Sekunden
das gefertigte Objektiv ist immer nur eine Näherung an das idealisierte Polystrehl-Diagramm
Der Polystrehl kann meßtechnisch am individuell gefertigen Objektiv nicht überzeugend dargestellt werden.
Das Optimum hinsichtlich bester Strehlwert bzw. Gaußfehler=Null schwankt zwischen Blau und Rot und kann nachträglich korrigiert werden
Fertigungs-Fehler, Astigmatismus, Koma und Spherical (teilweise) müßten zu Vergleichszwecken generell abgezogen werden
Die Meßpunkte auf der Gesamt-Skala im Farbspektrum sind nicht definiert, werden oft willkürlich gewählt
Die Bandbreite der verwendeten Interferenz-Filter ist ebenfalls undefiniert, eine Gewichtung ist nicht festgelegt
Nicht festgelegt ist, ob der Polystrehl-Wert vom Fokuspunkt Grün aus ermittelt wird, oder isoliert über jeden spektralen
Meßpunkt Bei Test-Reports namhafter Hersteller sucht man meßtechnische Polystrehl-Diagramme vergebens --- macht keiner
Die Vermessung und Berechnung ist eine Sache von Stunden. Siehe auch E006A
Damit bleibt das Polystrehl-Diagramm ausschließlich eine idealisierte, theoretische Darstellung eines Designer-Programmes
und ist nur äußerst zeitraubend meßtechnisch darstellbar, wobei die Frage nach dem Informations-Wert noch gar nicht
beantwortet ist. Schließlich findet man zwar idealisierte PolyStrehl-Diagramme aus Design-Programmen, nicht aber meßtechnisch
erzeugte Darstellungen, besonders nicht im Rahmen eines Test-Reports.
Dazu im Gegensatz ist die RC_Indexzahl das Ergebnis von mindestens drei konkreten Messungen zur Bestimmung Longitudinal
Aberration auf der opt. Achse vom Fokus-Punkt Grün=e-Linie=546.1 nm wave. Der Gaußfehler ist bei diesem Verfahren nicht
integrierbar. Ob dieser ein wesentliches Unterscheidungs-Kriterium sein kann bei einer so uneinheitlichen Situation von
individuell gefertigten Objektiven, ist ebenfalls völlig offen.
E029B Systematik - Planflächen prüfen
Bei Planflächen ermittelt man die Power, Radius bzw. die Planität, die möglichst gegen Unendlich gehen sollte. Planspiegel haben auch
andere Flächen-Verformungen, z.B. Astigmatismus, sphärische Aberration und andere Unregelmäßgkeiten. Wie bei anderen Optiken auch,
richten sich die ermittelnden Werte nach der Verwendung dieser Planflächen. Als Fangspiegel in einem Newton-System sollte die Planität
möglichst bei Null liegen, weil ein "Radius" auf der Planfläche bei der 45° Verkippung im Strahlengang zu Astigmatismus führt. Auch
sollte der Fang-/Planspiegel keine torische/astigmatische Verformung haben, ebenso keine sphärische Aberration.

http://r2.astro-foren.com/index.php/de/10-beitraege/02-ed-optiken-halb-apos-und-frauenhofer-systeme/578-b099-herschelkeil-lunt-und-baader-filterkurve-solar-continuum-baader
Planspiegel kann man entweder gegen eine hochgenaue Referenz-Planfläche prüfen, was aber voraussetzt, daß beide Flächen nicht
belegt sind: Ist der Fangspiegel belegt, dann bekommt man bei den Interferenz-Streifen kaum noch Kontrast, und kann diese nur
sehr schwer auswerten. Der Vorteil der Prüfung gegen eine Referenz-Planfläche ist, daß man auch die Planität exakt darstellen kann.
Siehe die beiden unteren Bilder als Gegenüberstellung.
Während bei der Prüfung auf Kontakt nur die Planfläche gegen eine Referenz-Oberfläche geprüft werden kann, kann man mit einem Referenz-Kugelspiegel
die Planfläche hinsichtlich der Wellenfront-Fehler prüfen. Bei einem Newton-System steht der elliptische "Fangspiegel" im Winkel von 45° im Strahlengang,
sodaß sich die elliptische Oberfläche perspektivisch zu einer Kreisfläche verkürzt, die wiederrum sehr genau im doppelten Durchgang geprüft werden kann:
Entweder mit dem Artificial Sky Test auf Abbildungs-Qualität, oder über ein Interferogramm auf einen Strehlwert.
Besonders bei belegten ellipt. Flats/Fangspiegel kann man nur gegen einen Referenz-Kugelspiegel prüfen. Der Test-Aufbau entspricht
dann - wie im obersten Link zu sehen - der 45° Position in einem Newton-System. Man prüft deshalb den Fangspiegel auf die Eigen-
schaften, wie er sie später im Strahlengang des Newton-Systems haben sollte. Ein signifikanter Astigmatismus wäre das z.B. ein
Hinweis auf mangelnde Planität.
Die beiden Bilder zeigen den Unterschied: Links eine Prüfung auf Kontakt, sehr kontrast-arm und rechts im 45° Winkel gegen eine Sphäre.
Herstellung und Auswertung rechts ist ohne Probleme, die Auswertung der Kontakt-Prüfung scheitert bereits an der Software.


siehe auch: http://www.astrotreff.de/topic.asp?ARCHIVE=true&TOPIC_ID=6586&whichpage=3
http://r2.astro-foren.com/index.php/de/10-beitraege/02-ed-optiken-halb-apos-und-frauenhofer-systeme/578-b099-herschelkeil-lunt-und-baader-filterkurve-solar-continuum-baader
Ein vorläufiger Entwurf für einen doppelten Test-Report - wird später überarbeitet.
E083 Überkorrektur bei Triplets beseitigt - 2016
Siehe auch: A049A Triplet 130-860 - auf der Suche nach der Ursache
Die historischen Zeiss-B Objektive, Triplets wie viele heutiger APO-Objektive, reagierten im Verlaufe von mehreren Jahrzehnten
mit einer Überkorrektur des Systems: Der Grund bestand im "Schrumpfen" der Distanz-Plättchen durch die thermische Bewegung
vom Glas, das die Plättchen minimal zusammendrückte. Damit verringerte sich der ursprüngliche Abstand vorwiegend von Linse L1
und L2. Um das zu korrigieren, mußte man durch Einsetzen neuer Distanz-Plättchen den ursprünglichen Abstand wieder herstellen.
Im vorliegenden Fall reagierte dieser Drei-Linser ebenfalls erheblich überkorrigert im Bereich PV L/2, sodaß man vermuten kann,
daß der Abstand zwischen L1 und L2 falsch bzw. viel zu gering vom fernöstlichen Hersteller eingestellt worden war. Dieser hatte
lediglich einen Distanzs-Ring von 0.15 mm eingelegt, während für dieses System erst ein O-Ring mit 4 mm Querschnitt zu einer
brauchbaren Lösung führte. Als fotografisches System, wäre selbst diese Überkorrektur ohne Beeinträchtigung, weil auch dieser
Fehler innerhalb der Auflösung des Kamera-Sensors liegt (könnte sein, daß der Hersteller so kalkulierte). Nur visuell wird man
ein derartiges System kaum akzeptieren, und es gibt ja Sternfreunde, die nicht nur fotografieren möchten.

-
Unter visuellen Gesichtspunkten kann man dieses Ergebnis nicht akzeptieren. Eindeutig nachweisbar ist die Überkorrektur mit dem Ronchi-Test.
Beim Artificial Sky Test (3-5µPinhole und Höchstvergrößerung) macht sich die Überkorrektur über die Energie-Verschiebung in die Beugungs-Ringe
bemerkbar bei gleichzeitiger Reduzierung des Maximums. Das Sternscheibchen wird dadurch etwas "aufgeblasen".
-
Die mittlere Linse ist gewöhnlich eine Plus-Linse, während L1 und L3 negative Brechkraft haben. Über zwei Abstands-Ringe von jeweils 0.15 mm
lassen sich alle drei Linsen seitlich zentrieren, womit man einen leichten Keilfehler ausgleichen kann. Über die mittlere Linse L2 kann das Triplet
zentriert werden, indem man so die Achskoma beseitigt nach folgender Regel: 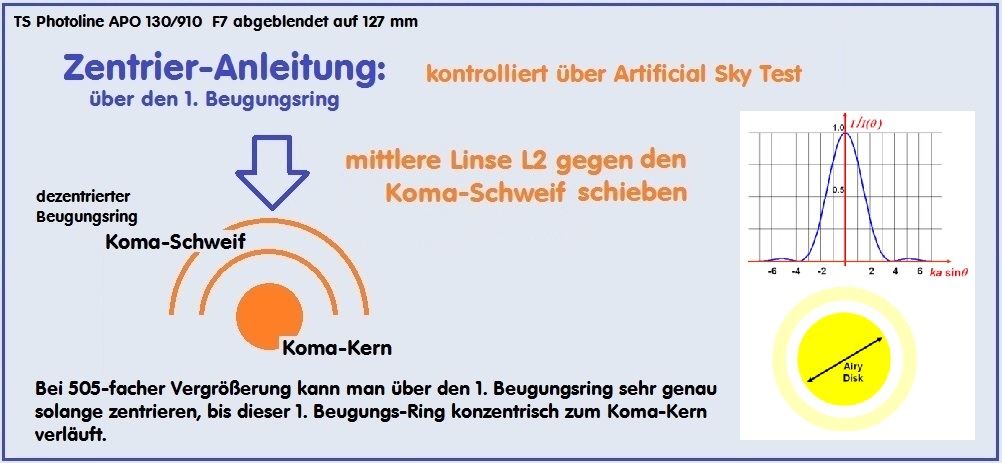
-
Die Einzel-Linsen in diesem Block lassen sich sich leider sehr leicht verschieben, und damit auch die 0.15 mm dünnen schwarzen Kunststoffringe.
Ohne Papier-Manschette kann man das sehr schwer korrigieren, sodaß sich beim Zurücksetzen des Linsenblockes in die Fassung die Distanzringe
sehr leicht verkanten und damit unbrauchbar werden. Schon aus diesem Grund ist eine Papier-Manschette dringend erforderlich.

-
In einer Übersicht das vorbereitete Equipment.

-
Die Halte/Schraubringe haben oben, ähnlich einer Schlitzschraube, kleine Nuten, in die der "Schlüssel" eingesetzt wird, der in meinem
Fall variabel einstellbar ist.

-
Mit einem kleineren Zylinder wird der Linsenblock von der Rückseite der Fassung herausgehoben, der aus Sicherheits-Gründen eine
Papier-Manschette bekommt, um so die seitliche Verschiebung der Linsen zu verhindern. So kann man den gesamten Linsen.Block
vorsichtig herausheben.

-
Der 4 mm im Querschnitt dicke O-Ring hat zunächst einen etwas größeren Durchmesser, damit man ihn in die Fassung einpassen kann.
Dabei sollte er ohne Spannung sich selbst an den Rand der Fassung drücken, wenn der zusammen mit dem Linsenblock wieder eingefügt
worden ist.

-
Die grüne Papier-Manschette soll ein seitliches Verschieben einer der 3 Linsen vermeiden, und damit vor allen das Herausfallen der
dünnen Distanz-Ringe. Beim Einlegen des 4 mm O-Ringes ist diese Manschette ebenfalls sehr nützlich, bevor die 1. Linse wieder aufgelegt
wird. Der Streifen läßt sich leicht verschieben, wenn man die Finger etwas anfeuchtet. Wenn der O-Ring spannungsfrei vorher in die
Fassung eingepaßt worden war, dann läßt sich der gesamte Linsen-Block problemlos in die Fassung zurückführen, ohne daß einzelne
Linsen verkanten würden.

-
Bei solchen Arbeiten ist das Hauptproblem, daß sich Staub aus der Luft an den geöffneten Flächen festsetzt. Deshalb sollte man möglichst
nicht über diesen Flächen arbeiten und die 1. Linse so abheben, daß die Innenfläche immer nach unten zeigt und dann nur an drei Punkten
aufliegt. Je öfter man einen solchen Linsenblock auseinander nimmt, umso mehr können sich die unbeliebten Fussel in der Fassung breit-
machen. Ein prüfender Blick gegen eine helle Lampe kontrolliert am Schluß, ob sich die ungeliebten Fussel eingeschlichen haben.
Grundbedingung für derartige Arbeiten ist eine völlig entspannte und ausgeglichene Verfassung in einem Raum, in dem man nicht gestört
werden darf. Jede Hektik, jeder "Druck" wirkt sich auf die Arbeitsweise aus und erzeugt in der Regel "Flurschaden". Nachdenken über
einzelne Arbeitsschritte und wie man "Bruch" möglichst vermeidet gehört unbedingt dazu. Nicht jeder Tag eignet sich für solche Arbeiten.

-
-
-
-
E029A RoC-Setup - fehlerhafte Auswertung beim Newton-Spiegel - Anleitung OpenFringe
Inhalt
- Bericht Teil 01: - Erfahrungen mit OpenFringe und dessen Fehler
- Bericht Teil 02: - Fehlerquellen bei der RoC-Auswertung
- Bericht Teil 03: - ein weiteres Beispiel
Bericht Teil 01: Erfahrungen mit OpenFringe und dessen Fehler
Astro-foren.de vom http://astro-foren.de/index.php/Thread/11243-Meade-ARC-203-2-2000/?postID=43809#post43809
Bei OpenFringe sollten es Interferogramme mit mehr Streifen sein. Die Frage ist jedoch, mit wie vielen Streifen entstehen sinnvolle Auswertungen. Bei 18 - 50 Streifen hätte auch OpenFringe noch kein Problem, sinnvolle Ergebnisse abzuliefern. Kritisch wird es bei 100 und mehr Streifen. Da würde iterativ, ohne daß irgend eine Einstellung verändert worden war, OpenFringe höchst unterschiedliche Strehl-Ergebnisse abliefern, was sehr verwirrend sein kann. Das Problem bei IGrammen mit viel Streifen besteht darin, daß man mit dem Auge die Fehler nicht mehr abschätzen kann, also nicht mehr plausibel wird, ob das Ergebnis stimmen kann oder nicht. Der Vorteil hingegen ist, daß man keine Streifen nachzeichnen muß. Allerdings sind die Ergebnisse bei wiederholter Auswertung nicht reproduzierbar, auch wenn keine der Einstellungen verändert wurden. Für diese Fälle ist die Fehler- suche fast aussichtslos, was bei AtmosFringe kein Problem wäre. Dieses IGramm liefert die unterschiedlichsten Ergebnisse ab: rohr.aiax.de/M_ARC_203-20.jpg There is no guarantee for the results are correct and a lot of bugs are in that program yet. With the same dates, outline-circles, FFT-shape you get different Strehl results, this cannot be correct. Deutlich trennen muß man zwischen RoC-Auswertung und der in Autokollimation oder der in Kompensation. In RoC wären die Eingabe für Durchmesser, Krümmungsradius und Wellenlänge exakt einzugeben. Aber auch der exakte Umkreis bei einem randscharfen RoC-Igramm ist ebenfalls wichtig. Die Lösung mit den Pfeiltasten ist gewöhnungsbedürftig. Bei IGrammen in Autokollimation wäre der exakte Umkreis nicht ganz so wichtig, weil die Zurückrechnung auf Null nicht notwendig ist. Hier ist die conic constant = 0. Der anschließende Report läßt sich übersichtlicher gestalten, die Variation über die Zernike Koeffizienten ebenfalls, positiv ist, daß das Programm sofort die neuen Ergebnisse anzeigt. Die 3-D-Wellenfront-Deformation bei beiden Programmen sind miteinander vergleichbar.

Eine komprimierte Anleitung folgt. Über eine Reihe von Ungereimtheiten stolpert man bei der Benutzung, die mit der Qualität der Interferogramme gar nichts zu tun haben.
Anleitung für OpenFringe
Dowload: tech.groups.yahoo.com/group/in…/files/OpenFringe%20Beta/
Anzahl der Streifen zwischen 20 - 50 max.
==============================
Prg- starten in Verzeichnis
Menue Configuration\Mirror\Test Parameters eingeben
Load IGramm File\Open Interferogramm
Rechts Outside Ellipse aktivieren mit Punkt: Für Umkreis
Set ellipse points anwählen
mit Maus Punkt setzen: 09:00 und 15:00 Uhr
Center and Edge anwählen
Kreis korrigieren mit Pfeiltasten und shift + / -
Rechts Obstruction aktivieren mit Punkt: Für Inkreis
Set ellipse points anwählen
mit Maus zwei Punkte setzen: 09:00 und 15:00 Uhr
Center and Edge anwählen
(bei Obstruktion das gleiche Verfahren)
Kreis korrigieren mit Pfeiltasten und shift + / -
Menue FFT analysis anwählen
Rechts Center and Resize image to 640 x 640
Rechts FFT (oder 2.FFT anklicken)
Rechts darunter mit Pfeil-Buttons kleinen blauen Kreis vergrößern bis knapp
zu erstem "Beugungsscheibchen"
Rechts darunter 3.Compute Surface anklicken
Menue Wave Front List anwählen = Wellenfront-Darstellung
Rechts Report anwählen und Zernike Based anwählen wegen PV
Menue o Zernikes view terms : mit Koeffizienten "spielen"
dis_able All = Strehl = 1.000
Enalbe Spherical Only für sphär.Aberr
============================================================================
Some notes for Dale Eason, the developer of Open Fringe:
If fringes maps created, there are a lot of problems with it:
- a lot of artefact in the map itself
- a low contrast of the fringes
- no sharp edges
- many or not many fringes
- three different setups and their conditions: RoC, compensation, autocollimation
- setup influences: vibrations and air turbolenses
- storing the optics, or how to store them
These all you have to respect in creating that maps and later, to calculate that maps.
There are two ways for calculation the PV, RMS and Strehl Value:
01. you calculate it with the fringes, in that case you can controll this by your eyes
02. you can calculate this with a FFT program Open Fringes and you cannot evaluate, whether the result is correct or not.
And sometimes with special fringes maps you get different results without varying any parameters. You just recalculate the
procedure.
With AtmosFringe I work for many years, and I had the controlling part in practice. A program becomes better, if you
work with it every day and you find out all the bugs of it. Open Fringe has many bugs yet.
So I tried to check how Open Fringe works with three types of fringes maps:
- normal but different created fringes maps (532 nm , 632.8 nm, 486.1nm till 656.3 nm wave)
- artificial with ZEMAX created fringes maps at 550 nm wave
- irregulary fringes maps what AtmosFringe can calculate, but not Open Fringe. The following is one of that.
At the end I will collect the bugs in a list for the programmer in the hope, he will correct this. This you can
take as a invitation, to have a dialog in English on our forum about OpenFringe. The main advantage is, you
can insert all diagrams, pictures for explane matters.
May be a translater could help you for the German text.

Mit OpenFringe habe ich mich auf unterschiedliche Art befaßt - ein Fringes Map Auswertprogramm auf Basis der FFT Fourier Transformation. Dabei
verwendete ich sowohl ZEMAX-generierte Interferogramme, deren Strehl man sich von Zemax bereits ausrechnen lassen kann, und Interferogramme,
wie sie bei unterschiedlichen Wellenlängen bei diesem Beispiel entstanden.
Der allgemeine Eindruck von diesem Programm ist, daß es eher mit einem Gemischwaren-Laden vergleichbar ist. Das Programm enthält also
Funktionen, die absolut nichts mit Streifenauswertung zu tun haben, wie die Simulation von RonchiGRammen, Foucault-Bildern, Sterntest
intra/extrafokal usw. Dadurch vermisst man eine klare Linie auf das eigentliche Ziel, nämlich die Auswertung von Interferogrammen.
Im Bereich der IGramm-Auswertung bestehen einige Unschärfen. Bereits bei unproblematischen IGrammen in Autokollimation, wo keine
Zurückrechnung auf Null stattfindet und demzufolge sowohl die Durchmesser- wie Fokus-Eingabe entfällt, entstehen auch bei gleichem
Um- und Inkreis, bei gleicher Größe der "blauen Kreis-Scheibe" bei der FFT-Analysis höchst merkwürdige und unterschiedliche Ergebnisse.
Sie können mit den Artefakten der IGramme zu tun haben, und genau deshalb wäre dann die normale Streifenauswertung sicherer, weil
man die Ursache direkt sehen könnte beim Autotracing.
Nach einiger Zeit gewöhnt man sich an die "Programm-Führung" - benutzerfreundlich ist es dennoch nicht, da müßte das Programm gründlich
überarbeitet werden. Selbst im Vergleich mit einem Streifen-Auswert-Programm ist man noch unsicher, welchem Ergebnis man mehr vertrauen
soll: Das liefert manchmal OpenFringe ab, manchmal AtmosFringe. Die notorischen Kritiker glauben natürlich immer nur an das schlechtere.
Nur ein Beispiel für seltsame OpenFringe Ergebnisse:
Ein Interferogramm kann man mit einem normalen PaintProgramm zeichnen. Mehrere schnurgerade Linien in Kopierfunktion genommen, und
mehrmals untereinander gesetzt, mit einem Umkreis versehen, und die Linien außerhalb beseitigt. Bei diesem artificial IGramm kann zwar
Astigmatismus vorkommen, aber ganz bestimmt keine sphärische Aberration - da müßten die Streifen "M"- oder "W"-Förmig verbogen sein.
Über die unregelmäßigen Streifenabstände kann Astigmatismus angezeigt werden.
Aus dieser Logik heraus macht AtmosFringe genau das, was zu erwarten ist. Deaktiviert man Astigmatismus und vorsichtshalber auch noch Coma, dann
muß der Strehlwert sehr hoch sein, was mit 0.998 auch tatsächlich eintrifft.
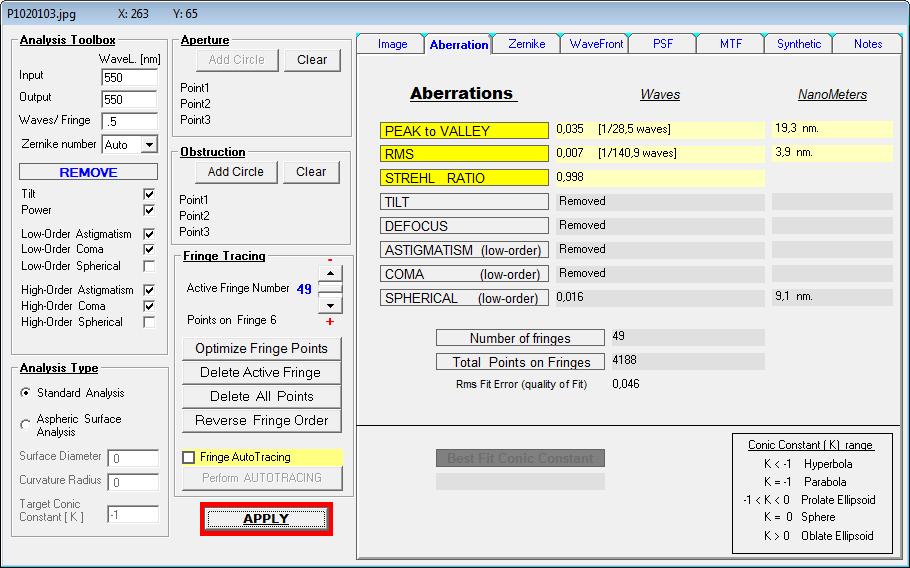
Nicht so bei OpenFringe: Hier wäre ebenfalls Astigmatismus und Coma deaktiviert, nur bekommt man gar keinen Strehlwert mehr und nur noch
eine Fantasie-Wellenfront-Darstellung. Das ist eines der Beispiele, wo OpenFringe überfordert ist obwohl es tatsächlich manchmal auch funktioniert.
Mag sein, daß der Programmierer keine Lust mehr hat, oder einfach zu wenig Rückmeldungen zu den Bugs abgeliefert wird. So ein Programm
muß konsequent in der praktischen Anwendung entwickelt werden, sonst wird das nichts.
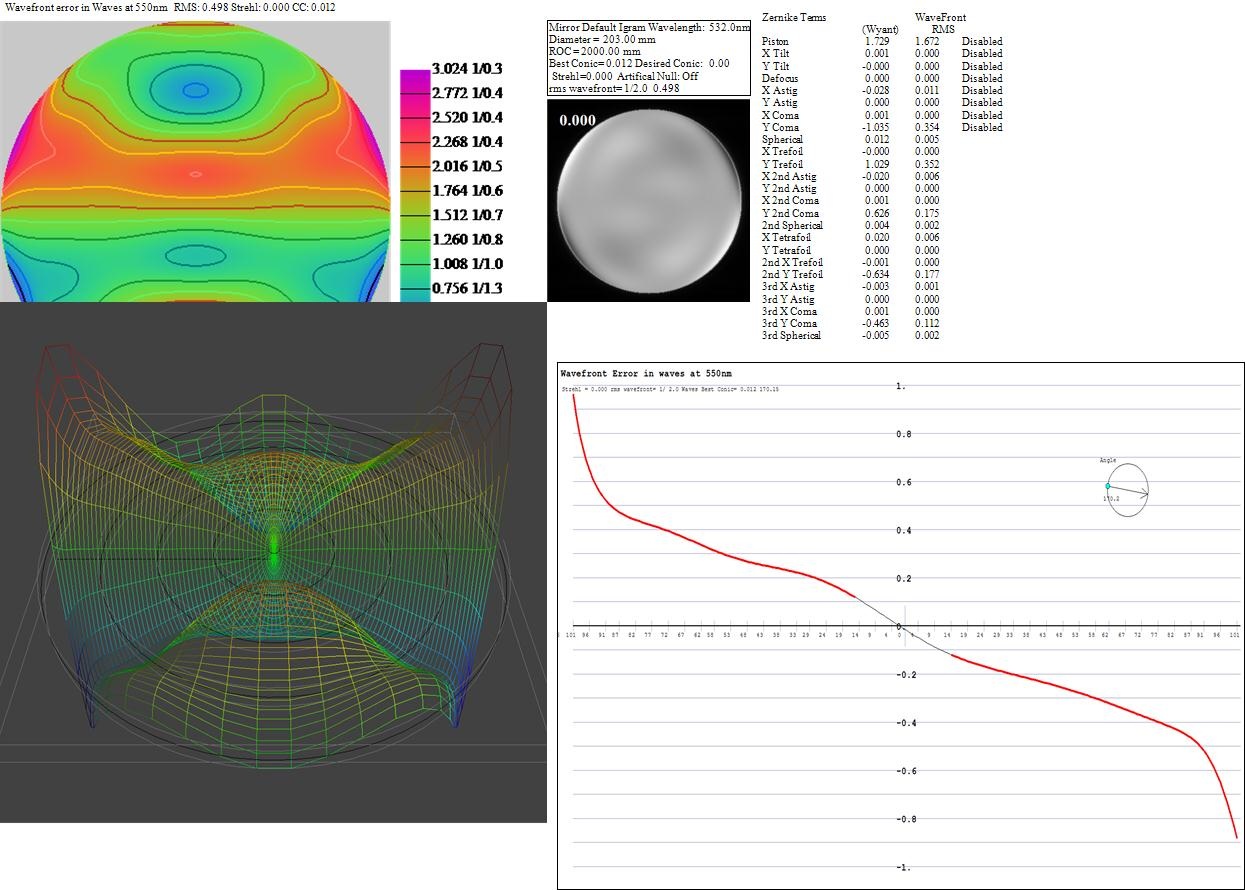
Liste der Bugs:
============
01. Den Um- und Obstruktions-Kreis eines IGrammes kann man speichern. Wer aber danach das gleiche IGramm erneut lädt und dazu
passend die gerade gesicherten Kreise, erlebt, daß nunmehr beides versetzt zueinander ist. Die DurchmesserGröße stimmt zwar
noch, nicht aber die Position, und die wäre in diesem Fall genauso wichtig, da ein Versatz von nur 1 Pixel bereits ein anderes
Strehlergebnis verursacht.
02. Bei Erase Ellipse werden Um- und ObstruktionsKreis gelöscht, nicht aber die beiden Punkte für den Obstruktionskreis. Die erst, wenn
man oben auf 'Obstructions' umschaltet.
03. Bei kleinerem Openfringe Fenster wird größeres IGramm verkleinert. Bei Fenstervergrößerung IGramm nicht mitvergrößert. "Center and
Resize image to 640x640" ist deaktiviert. Erst bei Zurückschalten von FFT Analysis to Interferogramm paßt sich die IGramm Größe an. Die Lösung mit Pfeiltasten die Kreise zu bewegen ist nicht benutzerfreundlich, dauert viel zu lange. Sinnvoll wäre jeweils den Mittelpunkt und den Radius der
Kreise anzugeben, damit sich die leichter reproduzieren lassen.
04. Bei wiederholtem Durchlauf verschieben sich beide Kreise unterschiedlich stark nach links und die Wellenfront zeigt Vertiefung in Mitte. Die Strehl-
Werte variieren um große Beträge. Zum Schluß kommt die Fehlermeldung: "Not all of mirror is visible inside image.Analysis aborted"
Nach Korrektur der Kreise ist es wieder OK.
T2
Bericht Teil 02: - Fehlerquellen bei der RoC-Auswertung
22.05.2015 Der obere Bericht Teil 01 ist ja immerhin bereits 6 Jahre alt, da kann sich einiges beim Auswert-Programm OpenFringe geändert
haben. Im Augenblick liegt mir ein Beispiel vor, bei dem es wieder einmal um eine OpenFringe-Auswertung in RoC geht (Radius of Curvature).
Hier bekommt der Stern-Freund schlechte Strehlwerte, vermutlich auch, weil die RoC-Auswertung höchst fehler-anfällig ist:

Auch bei einem 20-inch NewtonSpiegel Orion läßt sich zeigen, wie variabel die Strehlauswertung ist, und damit völlig abhängig von
der richtigen Eingabe des Krümmungsradius in mm, von der Eingabe des opt. wirksamen Durchmessers auf mm genau und schließlich,
wie man den Umkreis um das Interferogramm setzt. Da variiert bereits die Veränderung von 1 Pixel den Strehlwert. Ob also ein Spiegel
richtig korrigiert ist, muiß man entweder in Autokollimation oder gegen den Himmel prüfen. Es empfiehlt sich daher die Gegenprüfung
über ein anderes Setup.

Siehe den Bericht zum spiegel-eigenen Rest-Astigmatismus
Wenn der Rand eines RoC_Igrammes nicht kantenscharf ist, wäre das bereits der 1. Fehler der oberen Liste. Auch der opt. wirksame
Durchmesser muß bei der Auswertung stimmen. Der Radius in RoC gilt immer nur für die opt. Achse. Selbst wenn das stimmt, muß dieses
IGramm-Bild auch absolut rund sein, und nicht etwa elliptisch. Danach ist der IGramm-Umkreis des Bildes wichtig, weil bereits
Abweichungen von nur 1 Pixel zu anderen Strehl-Ergebnissen führt. Wenn also der Bild-Rand des IGrammes unscharf ist, dann darf man
nicht erwarten, den richtigen Strehl-Wert zu bekommen. Eine solche Auswertung führt schnell zu falschen Ergebnissen, und diese
müssen dringend überprüft werden, ob sie überhaupt plausibel sind. Ein einfacher Test wäre am Himmel der Ronchigitter-Test, weil man
in jedem Fall prüfen kann, ob die sphärische Aberration tatsächlich so unterkorrigiert ist, wie es die RoC-Auswertung zeigen würde.
Am sichersten ist immer noch der Test gegen einen Planspiegel - Autokollimations-Setup genannt. Nur hat nicht jeder einen guten Plan-
Spiegel mit Bohrung. [ Wenn beim IGramm-Bild oben der Umkreis nur 5 Pixel größer oder auch kleiner ist wegen Randunschärfe des
RoC-IGrammes, dann reduziert sich durch diesen Fehler der Strehlwert bereits auf ca. 0.910. Wobei hier über ZEMAX alle Werte
305 R 3048 mm eingehalten worden sind.]
Bei diesem Beispiel läßt sich der F/3.47-Spiegel in RoC überhaupt nicht mehr sicher auswerten. Bereits bei Eingabe des Durchmesser
von nur 3 mm Differenz, 288 - 291 mm 'springt' der Strehl von 0.715 auf 0.947 . Ohne Gegenkontrolle über ein anderes Setup geht es also
überhaupt nicht. Die RoC-Auswertung ist für "schnelle" Spiegel unbrauchbar. Da wäre eine Auswertung in Kompensation durch eine
Plankonvex-Linse zuverlässiger.
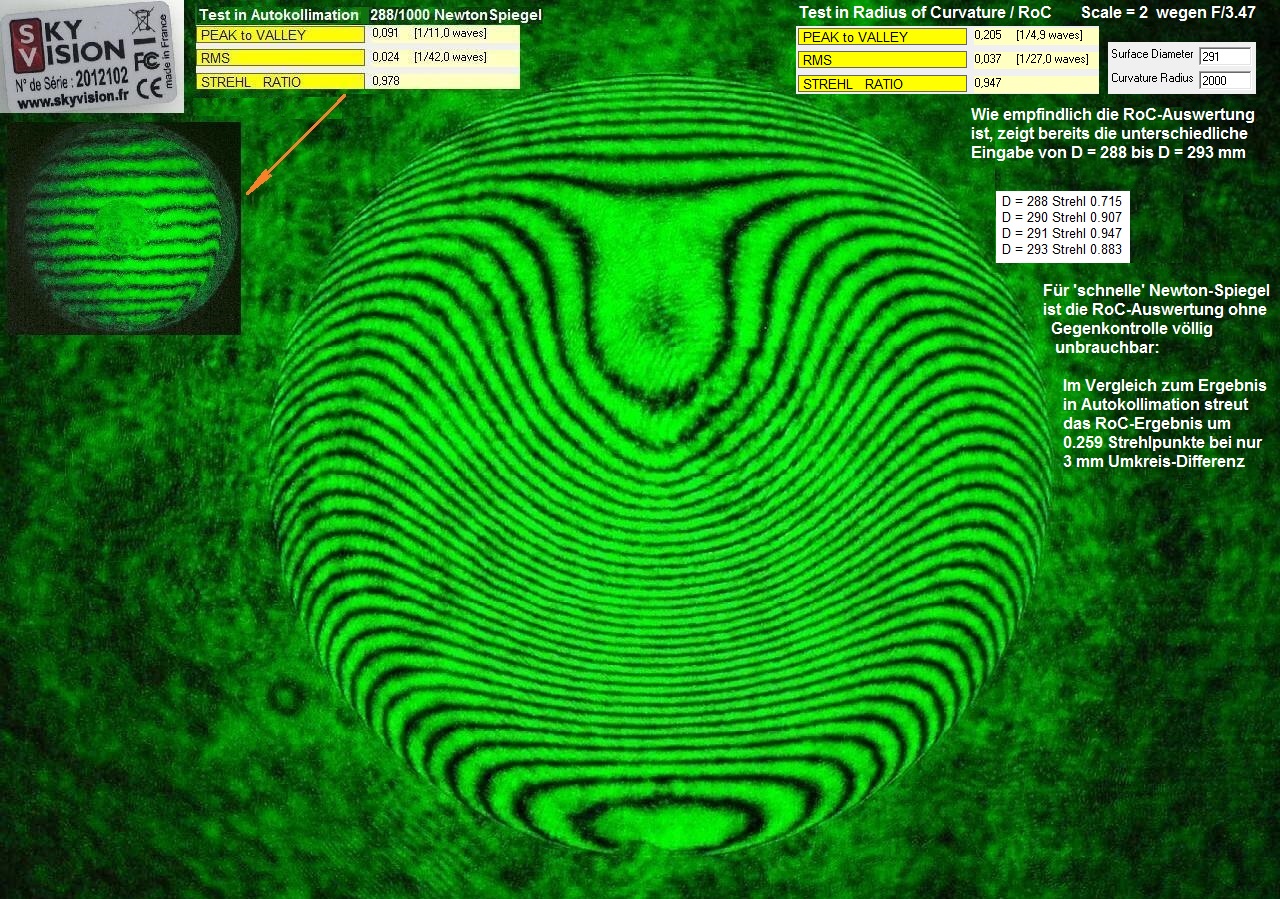
Im folgenden Bild ist der linke und rechte Rand eines IGrammes eingeblendet, das sich gleich aus mehreren Gründen NICHT aus-
werten läßt: Der Rand ist nicht kantenscharf und hat demzufolge einen deutlichen Einfluß auf die Strehl-Auswertung. Ob a) der
opt. wirksame Durchmesser des Spiegels eingegeben wurde, und ob b) der Umkreis des IGramm-Bildes pixelgenau richtig gesetzt
worden ist, ist über OpenFringe nicht nachvollziehbar. Ohne Kontroll- und Gegenmessungen ist diese Art RoC-Auswertung wertlos,
wie überhaupt eine isolierte Auswertung ohne Gegenkontrolle fragwürdig ist. Mangels Erfahrung kann man sich leicht täuschen.
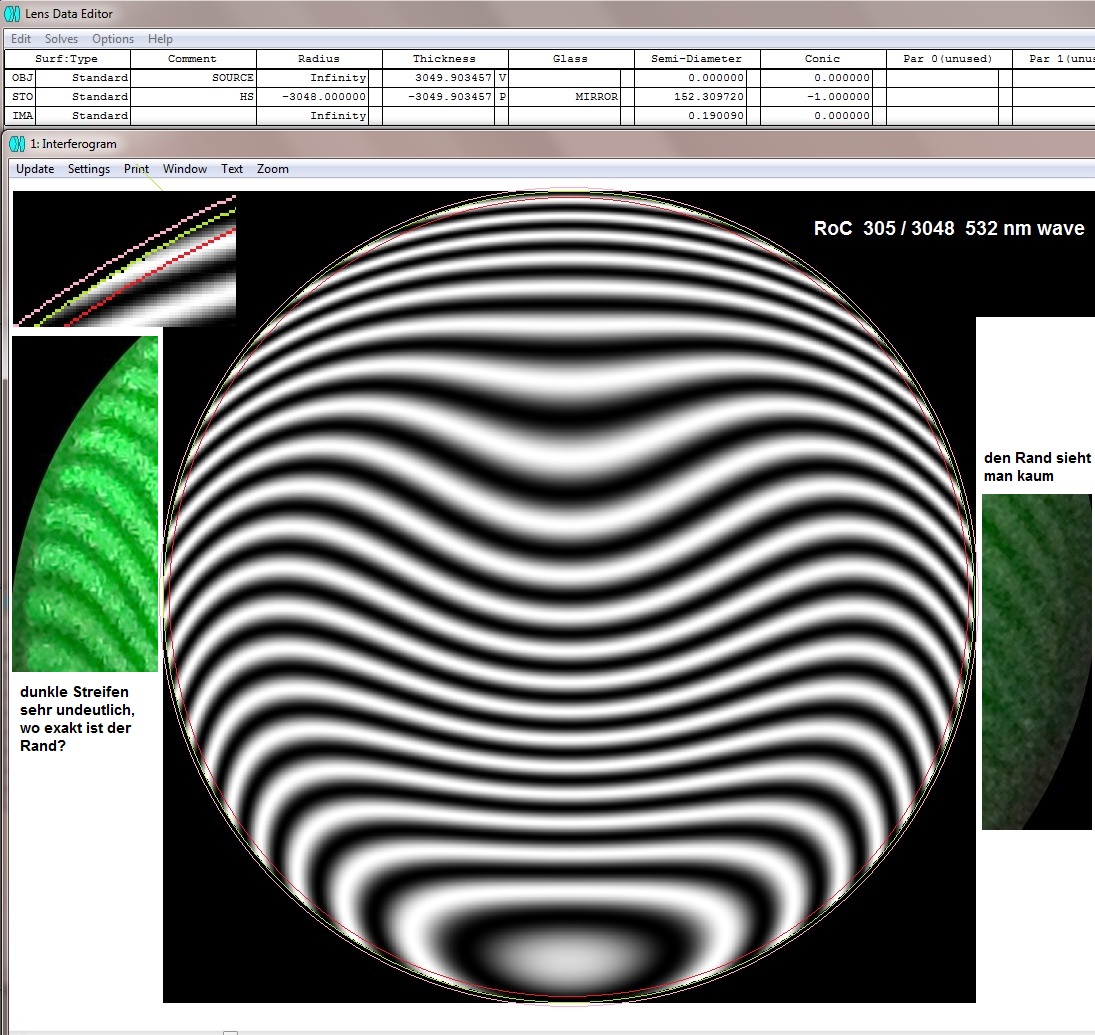
Wie anfällig das fragliche u. unscharfe RoC-IGramm tatsächlich ist, zeigt das folgende Beispiel, bei dem nur der opt. wirksame Durch-
messer von 305 mm auf 294 mm variiert wurde wegen der Möglichkeit, daß dieser Wert nicht sorgfältig genug ermittelt worden sei.
(Man könnte auch den Umkreis Des RoC-IGramm-Bildes bei der Auswertung variieren, oder den RoC-Radius)
In jedem Fall läßt sich der Strehlwert heftig variieren, ohne irgendeine Sicherheit, welcher Strehl-Wert denn nun stimmt.
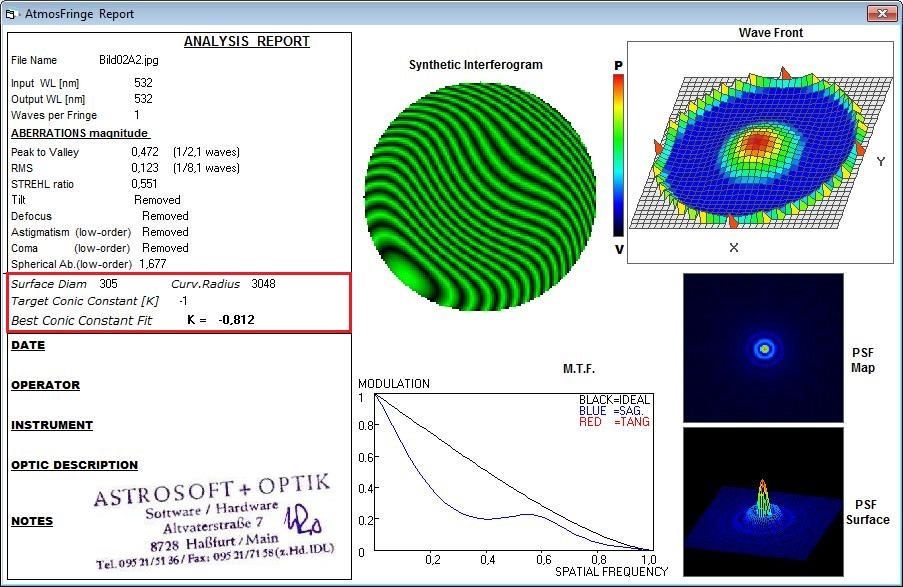
Nun wurde der Radius 294 mm eingegeben, und der Strehlwert springt auf 0.942 . Damit ist nur eines wirklich klar: Derartige
Werte führen keinesfalls zu sinnvollen und verläßlichen Ergebnissen. Man braucht dringend eine Kontroll-Messung über einen
anderen Testaufbau. Hat man aber weder einen Planspiegel, noch eine Kompensations-Linse, noch ein ZEAMX-Programm, mit
dem sich die genauen Abstände rechnen ließen, dann bleibt nur der Ronchigitter-Test am Himmel, ob nämlich die heftige Unter-
korrektur bei einem Strehlwert von 0.550 tatsächlich real ist. Erst dann wird die Sache etwas glaubhafter.
Beim Abzug von Astigmatismus sollte man aber sowohl den Low Order Astigmatismus und den High Order Astigmatismus abziehen.
Vorher empfiehlt sich unbedingt ein Test auf Rest-Astigmatismus.

Somit wird der "Vorteil" eines RoC-Testes sofort infrage gestellt, weil die Strehlermittlung von vielen Variablen abhängt,
die unbedingt stimmen müssen. Beim Test in Autokollimation ist das viel sicherer, auch der Roß-Null-Test ist sicherer,
wenn man über ZEMAX die exakten Abstände von Linse zu Newton-Spiegel berechnet hat. Somit hat die Forderung
nach einer Kontroll- oder Plausibilitäts-Messung unbedingt seine Berechtigung. Siehe auch: E029 -Test-Anordnungen astronomischer Optiken
T3
Beim Vermessen von Newton-Spiegeln muß man die Fehlerquellen einzelner Testverfahren im Auge behalten. Dabei ist das RoC-Verfahren
besonders fehleranfällig, weshalb man dringend gegen einen guten Planspiegel prüfen sollte. Dieses Verfahren ist ein absoluter Null-
Test mit einem geringen Fehleranteil bezogen auf die sphärischen Aberration. Deshalb muß eine Prüfung auf Rest-Astigmatismus vorgeschaltet
werden, damit man in Autokollimation nur noch die sphärische Aberration zu beurteilen hat, also Unter- oder Überkorrektur bzw. eine
perfekte Parabelkorrektur. Es geht um die ausschließliche Betrachtung des Öffnungsfehlers,also um Über- oder
Unterkorrektur. Dem 10" F4.7 Newtonspiegel sieht man die ca. PV L/4.5 große Überkorrektur deswegen an, weil sich die Streifen nach oben
durchbiegen. Der Ronchi-Gittertest 13 lp/mm intrafokal kommt zu einem gleichen Ergebnis.
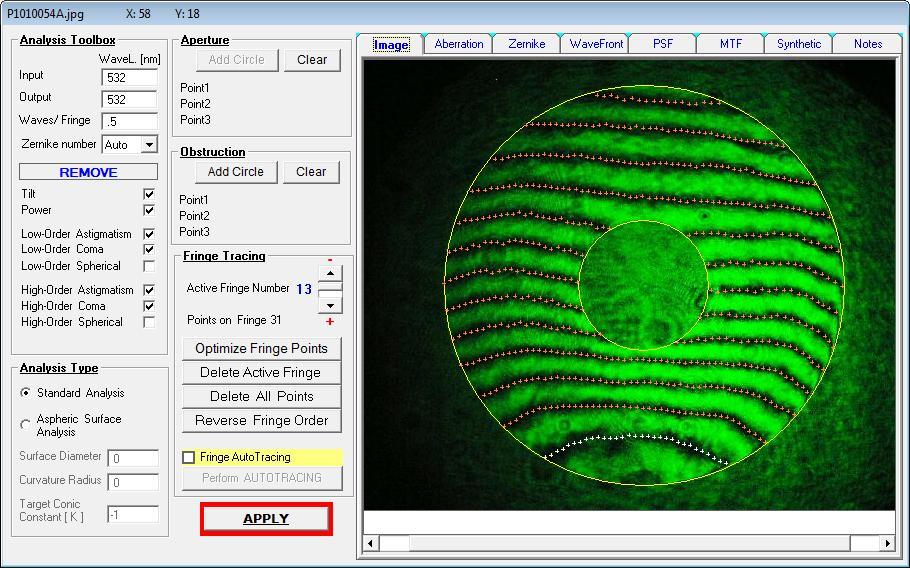
Das Strehlergebnis sollte deshalb der Wahrheit entsprechen. Insofern sollte die Auswertung in RoC (Radius of Curvature)
zu ähnlichen Ergebnissen kommen.
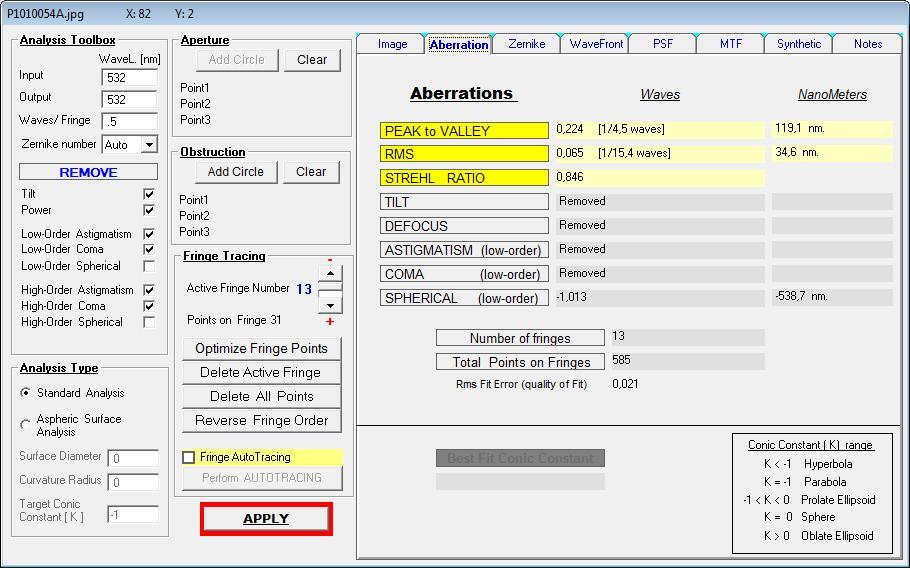
Eine der ersten Bedingungen dieses Interferogrammes ist ein kantenscharfer Rand, weil der Umkreis pixelgenau gesetzt werden muß.
Eine weitere Bedingung ist der opt. wirksame Durchmesser der Spiegelfläche und der Krümmungs-Radius mit einer Gen auigkeit von
mindestens 1 Millimeter. Die Meßwellen-Länge muß ebenfalls exakt eingetragen werden. Da sich das Auswertprogramm häufig verläuft,
empfiehlt sich das "Nachzeichnen" der Interferenz-Streifen, bei dessen Artefakten das Auto-Tracing häufig "aussteigt", und dann ohnehin
nachgearbeitet werden muß. Im konkreten Fall geht es um den richtigen pixelgenauen Umkreis.


Der Krümmungsradius wurde also genau vermessen, ebenso der Durchmesser, beide wurden richtig eingegeben. Nur der Strehlwert lag ca. 10%-Punkte
niedriger, sodaß man nun mit den Parametern förmlich spielen kann: Dabei stellt sich z.B. heraus, daß bereits beim Durchmesser ein 0.1 mm den
Strehlwert "springen" läßt. Auch der Umkreis bei der Auswertung war offenbar zu groß, sodaß zum ursprünglich weißen Umkreis noch ein
kleinerer in Rot dazu kam. Und erst jetzt entstand ein Ergebnis, das mit dem in Autokollimation erreichten Ergebnis vergleichbar war. Damit
ist die Auswertung in RoC äußerst unzuverlässig, was bedeutet, daß man dringend eine Kontrolle über einen anderen Testaufbau braucht:
Entweder in Autokollimation gegen einen Planspiegel, oder in Kompensation durch eine große Plankonverx-Linse.
Einen Vorteil wiederum hat die RoC-Auswertung. Man bekommt die gesamte Spiegelfläche gezeigt, und so bestätigt sich die Vermutung,
daß die Mitte des Spiegels zu tief retouchiert worden war - doch da wäre der ellipt. Fangspiegel und verdeckt das Ganze.
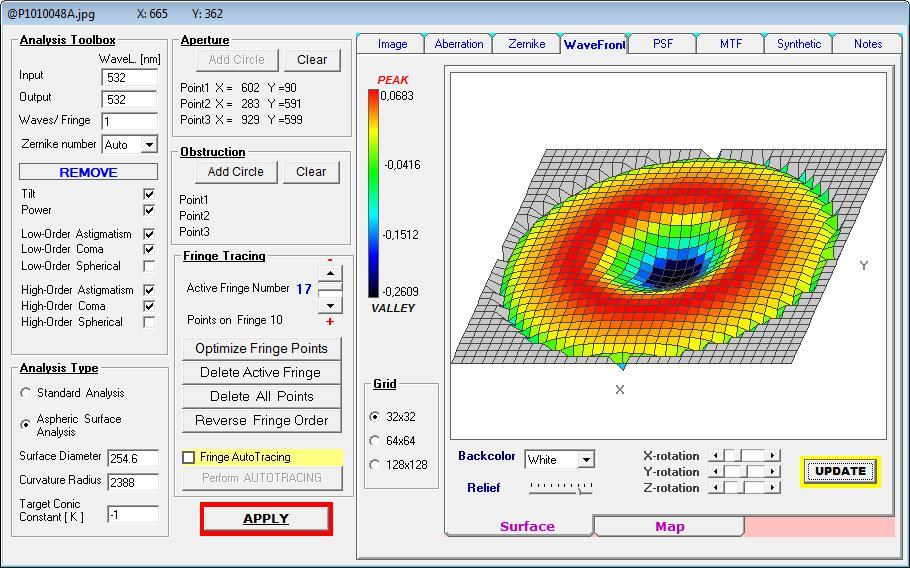
zum Anfang zurück:
E082 TAK 152-126 APO vor Planspiegel zentrieren
Vorbemerkung
Im einfachsten Fall prüft man ein Objektiv am Polarstern - vorausgesetzt, das Objektiv selbst ist im Tubus-Rohr exakt kollimiert,
was man über die Reflex-Bilder im Okularauszug erreicht. Ohne Seeing-Einflüsse geht das besser auf der opt. Bank. Entweder
man erzeugt über ein Newton-System einen künstlichen Stern, aber auch dieses Hilfsmittel muß perfekt, also koma-frei, zentriert
sein, oder aber man setzt das Objektiv samt Tubus vor einen Planspiegel, dann sieht man im Zentrum Okularauszug den künst-
lichen Stern und bei hoher Vergrößerung eventuelle Restfehler des Objektivs, also Astigmatismus, Koma und Spherical:
Bei höher Vergrößerung und einem Pinhole-Durchmesser von 5 - 10 µ, nicht mehr. Ohne einen Tubus muß man das Objektiv
vor dem Planspiegel zentrieren. Und wie das geht, zeigt folgender Bericht.
Bei einem ein opt. Tubus wird auf die Kollimation von Objektiv zur Tubus-Mittelachse großer Wert gelegt, sodaß man nur noch ein
Chesire-Okular braucht, um diesen opt. Tubus vor einem Planspiegel zu zentrieren. Aus Platzgründen bekommt man jedoch oft nur
das Objektiv selbst zum Testen, sodaß man ein Verfahren braucht, dieses Objektiv ohne Tubus vor einem Planspiegel zentrieren zu
können. Das folgende Verfahren verrät, in welchen Schritten das Objektiv vor dem Planspiegel zentriert wird.
Dazu eignet sich einer der üblichen (grünen) Laser-Pointer, den man in eine Halterung steckt und davor eine weiße Platte setzt,
wie auf dem Bild zu sehen. Dieses Laserbündel richtet man so auf einen Planspiegel aus, daß das Bündel den Flat mittig triff und
zwischen Flat und Laser noch genügend Platz ist, um in einem weiteren Schritt das eigentliche Objektiv vor den Flat gesetzt wer-
den kann. Zunächst muß das Laser-Bündel zum Flat selbst zentriert werden und später in diesem Testaufbau auch das Objektiv.
Das erfolgt in den folgenden Arbeitsschritten.:
Zunächst zentriert man den Laser zum Planspiegel und zurück.

Nachdem man vor dem Planspiegel das Objektiv eingefügt hat, wird man mehrere Fehler bemerken: Die Objektiv-Höhe stimmt
ebensowenig, wie die Neigung der Optik zur X-Achse, wie der seitliche Linsenversatz und schließlich die Drehung der Linse zur
vertikalen Drehachse. Betrachtet man jedoch die Reflex-Punkte auf dem weißen "Schirm" vor dem Laser, dann lassen sich alle
diese "Fehler" der Lage dieser Punkte zuordnen, und damit die Optik zentrieren. Die opt. Achse des Objektivs muß später mit
dem Laserbündel zusammenfallen.
Man beginnt sinnvollerweise zunächst mit der Verkippung der Linse zur X-Achse, also zum Laser-Bündel, das die X-Achse dar-
stellt.

Die diagonal angeordneten Reflex-Punkte bewegen sich bei der Verkippung der Linse auf eine horizontale Linie, wie sie auf der
weißen Platte erkennbar ist. Um auch die diagonale Lage der Punkte zu beseitigen, muß das Objektiv auf die richtige Höhe
gebracht werden, sodaß auf der eingezeichneten schwarzen Linie die zunächst diagonalen Reflex-Punkte horizontal zu liegen
kommen. Sie sind aber immer noch gespreizt. Das bekommt man auf Null, wenn man das Objektiv seitlich soweit vorsichtig ver-
schiebt, daß diese Punkt jeweils links und rechts in einen Punkt zusammen fallen. Man hat also jetzt links und rechts vom Laser
auf der schwarzen Linie je einen Punkt, der nur noch in den Laser-Ursprung "geschoben" werden muß.

Aus drei Reflex-Punkten im Bild vorher ist ist durch seitlichen Versatz der Linse in Y-Achse jeweils 1 Reflex-Punkt links und rechts geworden.
Nur sie müssen noch in den Laser-Ursprung "gedreht" werden. Das geschieht, wenn man das Objektiv in einer vertikalen Z-Achse dreht, sodaß
diese Reflex-Punkte sich dem Ursprung nähern, bis sie mit ihm zusammenfallen. Danach kann man sicher sein, daß das Objektiv perfekt auf
der opt. Achse zum Planspiegel steht. Bereits bei diesem Vorgang läßt sich erkennen, ob die Optik selbst zentriert ist, oder z.B. Achskoma
aufweist.
Der Artificial Sky Test zeigt bei höchster Vergrößerung in einer Art Übersicht alle opt. Fehler des Objektivs. In diesem Fall ist der
TAK APO perfekt zentriert und der neue Besitzer wird seine Freude daran haben, was ich natürlich jedem Hobby-Astronomen
wünsche.

http://rohr.aiax.de/@ZeissAS96927_07.jpg
Der Leser ist eingeladen, zu diesem Bericht einen Kommentar zu schreiben.
E081 Der das Gras wachsen hört . . . Beschichtung und Dicke
Die "GscheidHaferl" <bayerischer Ausdruck> wachsen auch bei den Hobby-Astronomen immer wieder nach. So konfrontierte unlängst
ein Sternfreund einen bekannten Spiegelschleifer mit der Frage, warum man von von der Rückseite eines Spiegels eine Lichtquelle
sehen könne. Und weil manche Zeitgenossen ja wirklich seltsam drauf sind, machte dieser Experte flugs ein negatives Qualitäts-
kriterium daraus: Die Beschichtung sei fehlerhaft, mangelhaft - und was diesem Freund noch alles eingefallen ist.
Gehen wir also dieser Frage in aller Gemütlichkeit nach:
Blattgold, seit Jahrhunderten/Jahrtausenden in Verwendung, überzieht die vergoldeten Gegenstände mit einem edlen Glanz, und wer
einmal kurz zu Test-Zwecken damit arbeitet, bringt es hernach nicht mehr vom Fingernagel herunter. Gerade als hätte man diesen mit
einem Lack überzogen. Hergestellt wird Blattgold in Schwabach bei Nürnberg. http://www.blattgold-rupprecht.de/ Dort kann man
sich ein dünnes Heftchen besorgen. Und dort erfährt man auch, auf welche Dicke das massive Gold "geschlagen" wird:
Die Blattstärke von Blattgold beträgt zwischen 1/7000 und 1/8000 Millimeter. Das ist der siebente Teil eines Mikrons oder 0,000142857 0
Millimeter oder 0,14 my. (Der Durchmesser eines Haares beträgt ca. 70 my und ist somit 500 mal so dick.)
http://www.br.de/mediathek/video/sendungen/geld-und-leben/geld-leben-goldschlaeger-100.html
Eine mit Blattgold belegte Figur - es ist im Übrigen eine hohe Kunst - wird man kaum von der Rückseite her daraufhin untersuchen können,
wieviel des Lichtes durch diese 0.3 Mikron bis 0.8 Mikron durchschimmern würde. Leider! (Denn besagter Astronomikus schließt ja messer-
scharf, daß das durchschimmernde Licht beim reflektierten Licht fehlt. Eine Gemeinheit aber auch!

-
Unter dem Mikroskop erscheint obige Blattgold-Folie im Durchlicht weit transparenter, als das bei Draufsicht oben vermuten läßt. Das wird auch bei Aluminium
nicht anders sein. Wesentlich ist die gleichmäßige Schicht-Dicke über die gesamte Fläche, da sonst die Optik verändert werden würde. Bei den dunklen "Adern"
liegt die Folie vermutlich zwei- oder drei-fach.
Wäre also dieses dünne Blattgold für die Beschichtung verwendet worden - vom optischen Durcheinander einmal abgesehen - dann wäre das fatal für die Reflektivität, so
man es von der Rückseite betrachtet bei einer Dicke von vermutlich 0.3 Mikron. Wobei ich auch schon einen 80 cm Spiegel mit einer Goldbeschichtung vermessen habe.
Und von hinten betrachtet, konnte man sehr gut durch die Beschichtung durchsehen.
Das folgende Bild läßt die Lichtquelle gut erkennen: Eine LED-Lichtquelle. Damit ist immerhin soviel klar, daß Beschichtungen dicker sind als ein Blattgold Leave.

-
Und nun untersuchen wir drei Spiegel unterschiedlicher Hersteller, unterschiedlichen Alters und unterschiedlicher Rückseite. Den Lichtenknecker Newtonspiegel habe
ich nun schon seit 40 Jahren und mehr.

-
Der mit Hilux beschichtete 8" Orion Optics Newton-Spiegel hat eine blanke Rückseite und die verwendete Lichtquelle erkennt man gut von hinten. Aber sehr viel
weniger , als beim Beispiel Blattgold. Also muß die Beschichtung dichter sein bzw. eventuell auch dicker als 0.3 Mikron. Messen kann ich das zunächst nicht.

-
Der Lichtenknecker-Spiegel ist hinten matt geschliffen. Also hilft ein Tropfen Waffen-Öl, der diese Rückseite transparent machen kann. Auch hier erkennt man wieder
die Lichtquelle. Die Dicke der Beschichtung sollte ebenfalls dicker als die des Blattgoldes sein.

-
Beim dritten Beispiel "bremst" die matte Rückseite ebenfalls den Lichtschimmer. Auch hier half ein Tropfen Waffen-Öl. Auch hier ist der Licht-Durchlass erheblich
geringer als beim Blattgold-Film. Man weiß beim Blattgold, daß bei der Außen-Vergoldung die Schichtdicke etwa bei 1 Mikron liegen sollte. Mehr
wird eine Spiegel-Bedampfung auch nicht auftragen, läßt sich vermuten. Zumal die Schichtdicke gleichmäßig aufgetragen werden muß, damit
man die opt. Qualität des Spiegels nicht beeinflußt.

-
Derartigen astronomischen Geistern wäre zu empfehlen, diese Vermutung mal gründlich wissenschaftlich zu erforschen, bevor sie mit unsäglichen
Vermutungen die Szene verrückt machen - während andere genau mit solchen Hilux verspiegelten Systemen die allerschönsten Beobachtungen
oder Fotos machen.
E013B Strehl und Wellenlänge
F037 Certifikate im Vergleich: Etwas für Perfektionisten , http://rohr.aiax.de/APQ97003_05.jpg
Aus dem oberen Bericht wird deutlich, daß z.B. die 'Firma Carl Zeiss Jena am 26.10.1993 für einen APQ eine
"Qualitäts-Urkunde für Astro-Optik" ausgestellt hatte, bei einer Wellenlänge von 632.8 nm wave. Zur damaligen
Zeit waren grüne Laser von einer Wellenlänge von 532 nm wave noch nichtallgemein verfügbar. Haupt-Problem
einer Messung bei 632. 8 nm wave ist der Umstand, daß ein üblicherweise auf Grün = 550 nm wave korrigiertes
Objektiv bei 632.8 nm wave bereits unterkorrigiert ist, während es im Bereich 550 nm wave perfekt sein sollte.
Das entspricht der maximalen Empfindlichkeit eines menschlichen Auges bei Tagsehen. Beim Nachsehen ver-
schiebt sich die maximale Empfindlichkeit ins kürzere Spektrum auf 510 nm wave, während unsere Augen dann
für das rote Spektrum bis auf ca. 10% "blind" sind. Aus diesen Grund wird bei vielen Achromaten der rote
Fokus möglichst weit nach hinten verlegt, weil diese Farbe für unser Auge am wenigsten wahrgenommen wird.
Die Wellenlänge von 632.8 nm wave, wie sie der Helium-Neon-Laser erzeugt, ist nur dann für einen Test-Report
sinnvoll, wenn die Linsen-Optik ihr Optimum im roten Spektrum hat, oder aber bei Spiegel-Optiken oder bei
Planspiegel-Messungen. Weil bei Linsen-Optiken das rote Spektrum ungeeignet ist, hat man zunächst das Strehl-
ergebnis von 632.8 nm wave auf 550 nm wave umgerechnet, bis sich auch ein grüner Laser bei 532 nm wave für
derartige Messung als sehr viel geeigneter herausstellte. Verwendet wird häufig der frequenzverdoppelte
DPSS-Laser (532 nm) unterschiedlicher Leistung.
Dabei gilt: Je kürzer die Meß-Wellenlänge, umso "schärfer" und genauer wird die Messung, was besonders auch
für die Chipherstellung gilt. Man bekommt also heute die üblichen Test-Reports in der Wellenlänge von 532 nm wave.
Das entspricht sehr viel mehr der Hauptwellenlänge Grün, wobei in der Optik-Rechnung bzw. der Literatur von
den Fraunhoferschen Spektral-Linien ausgegangen wird. Also für Blau = F-Linie = 486.1 nm wave, für Grün = e-Linie
= 546.1 nm wave, für Gelb = d-Linie = 587.6 nm wave und schließlich Rot = C-Linie = 656.3 nm wave und zugleich
die H-Alpha Linie.

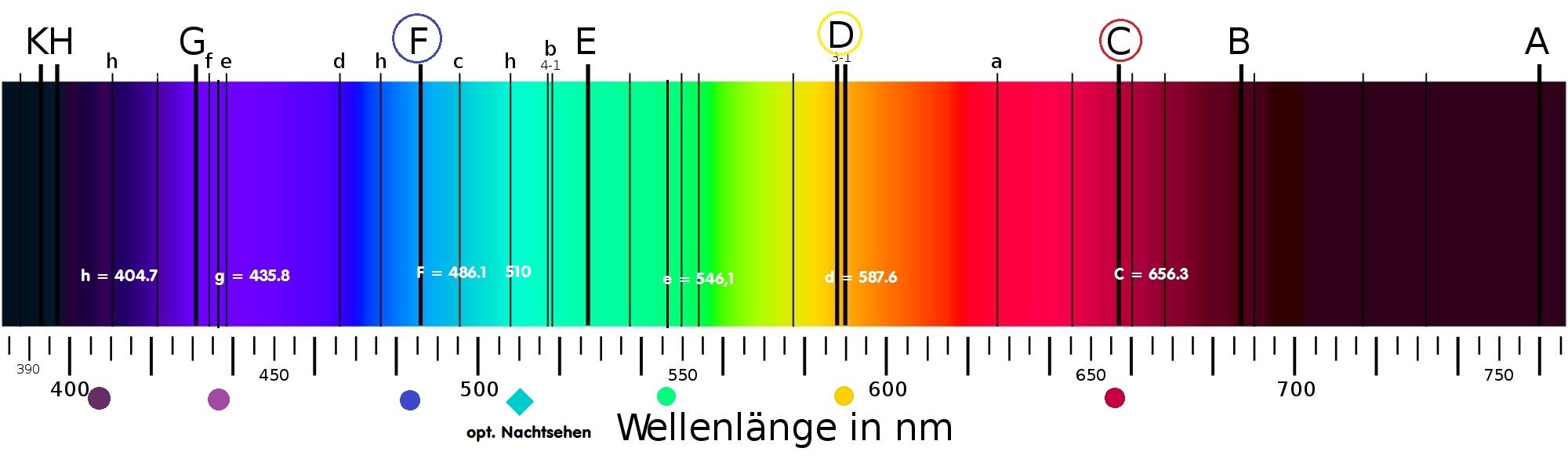
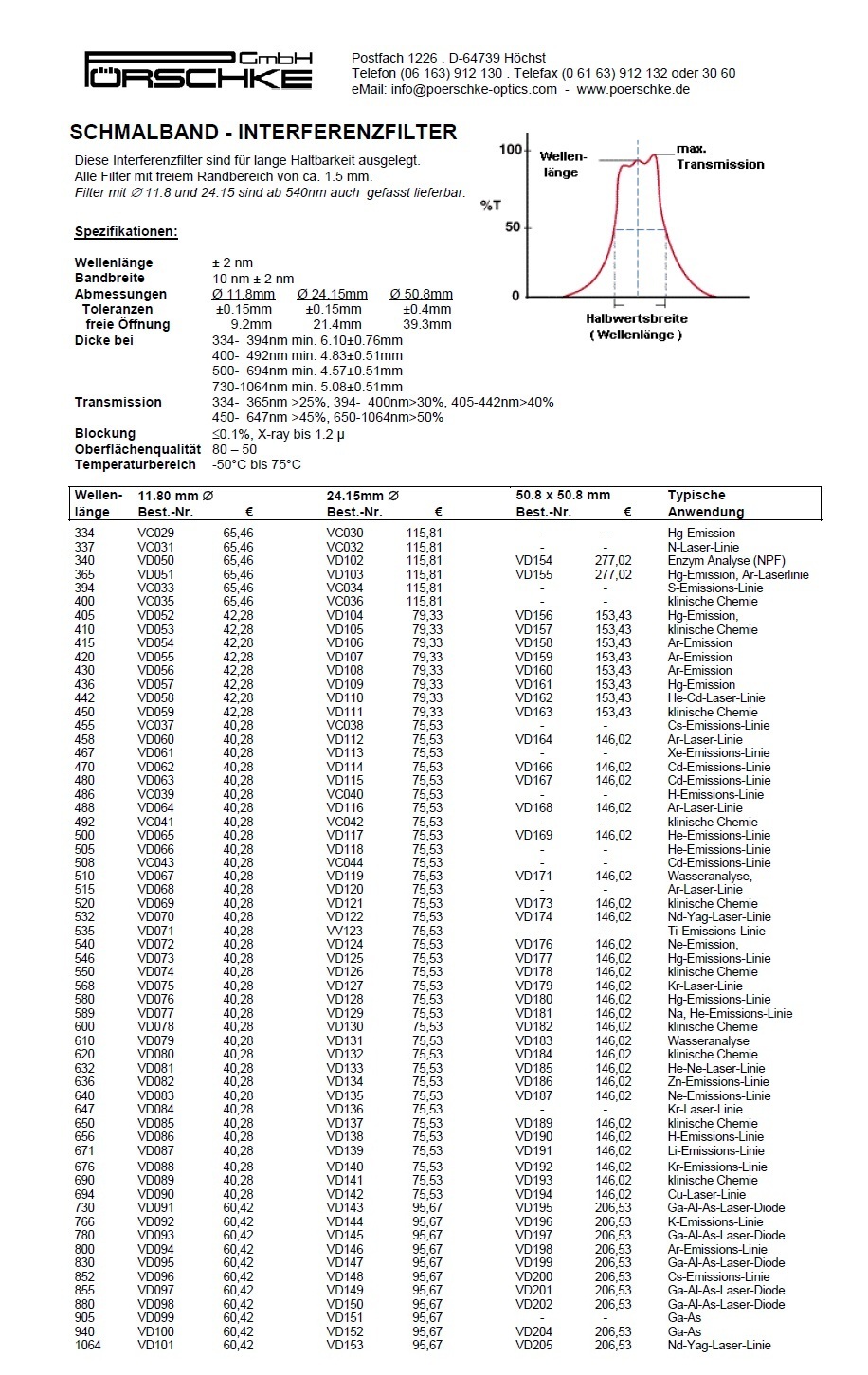

Ein Test Report der Firma LZOS vom 28.01.2014 weist bei 532 nm wave für einen Triplet Apochromaten Nr. 103
einen Strehl von 0.975 aus, einen Wert, den ich überprüfen sollte. Weil ich aber in den üblichen Wellenlängen
von F-, e-, d, und C-Linie Interferogramme erstellt habe, um zugleich über die Farbreinheit des Objektivs eine
Aussage machen zu können, erstellte ich nicht bei 532 nm wave sondern bei 546.1 nm wave ein Interferogramm.
546.1 nm wave liegt näher am Optimum des menschlichen Auges.
Mein Strehlergebnis lag bei 0.984 also etwas höher bzw. besser. Der Kunde war es aber nicht zufrieden, und
wollte nun den Strehl für genau 532 nm wave haben.

Auch kein Problem, das kann man umrechnen und so erhielt ich den Wert 0.983, was zum LZOS-Wert um nur
0.008 differiert. Beide Messungen ergeben eine Übereinstimmung, von weniger als 1% vom Strehl.
Für die Spektral-Farbe Blau würde der Strehlwert wieder deutlich sinken, weil dort die Überkorrektur und die
kürzere Wellenlänge den Wert reduziert.
Während LZOS sehr hochwertige Objektive ausliefert, die ihr Optimum in der Hauptfarbe Grün haben, liegt bei
vielen Objektiven das Optimum eher bei Gelb oder gar bei Rot, ganz selten bei Blaugrün = 510 nm wave, was
für unser Augen bei Nachtbeobachtung in den meisten Fällen am Sinnvollsten wäre.
Die Unschärfe in der Auswertung hängt auch mit dem Foto des Interferogrammes zusammen: Je mehr Artefakte
z.B. das Bild des IGrammes enthält, umso stärker streuen die Auswert-Ergebnisse. Das ist ein weiterer Grund,
warum ich lieber Weißlicht+Interferenz-Filter-Aufnahmen bevorzuge, deren Auswertung eindeutigere Resultate
erzeugen. Auch der Vorschlag in einem "averaging" viele IGramme auszuwerten und dann zu mitteln, beseitigt
das gerade erwähnte Problem nicht. Man muß sich damit abfinden, daß a) ein exakter Strehlwert immer eine
Unschärfe hat und b) welche Information darin steckt, wenn man den Strehl auf der 3. Stelle exakt zu erhalten
glaubt. Auch läßt sich die Qualität einer Optik nur zum Teil aus dem Strehlwert erklären !!
Je nach der Bildqualität der einzelnen Interferogramme haben die mehr oder weniger deutlichen Artifakte
einen Einfluß auf das Meßergebnis, was besonders mit der Lichtquelle und der dort verwendeten Optik zu tun hat.
Egal ob nun mein ermittelter Strehl-Wert exakt die gleiche Größe hat, wie der von LZOS zertifizierte oder
um einen geringen Wert variiert, es steckt keine wirkliche Information drin. Wenn beide Ergebnisse ziemlich
dicht beieinander liegen, spricht einiges dafür, daß die Wirklichkeit bei einem der beiden Werte oder irgendwo
in der Mitte liegt. Ein Strehlwert kann sich bereits ändern, wenn nur ein Punkt um wenige Pixel verschoben wird.

E080 * Zeiss Planspiegel Flat 520 mm Nr. 22 Testaufbau Autokollimation von 20-inch Newton-Spiegel
Zu diesem Bericht muß ich folgende Anmerkung machen:
Spiegel sollte man immer erst über mehrere Stunden temperieren lassen. Da kamen also unlängst gleich drei interessierte Sternfreunde
angerückt und warteten voller Neugier, was mit ihrem Spiegel passiert. (Der war aber nun leider nicht temperiert - und diese wichtige
Regel ging erst einmal in der Hektik unter.) Neben der Prüfung auf Rest-Astigmatismus erstellte ich in RoC ebenfalls ein Interferogramm
und merkte bei späteren Auswertung, daß auch hier der Spiegel anders reagierte, als er eigentlich sollte. Auch im Kompensations-Testauf-
bau hatte der Spiegel wohl immer noch nicht die richtige Form und reagierte überkorrigiert. Erst beim Testaufbau gegen den 500-Zeiss
Flat schien die Temperatur-Anpassung besser zu sein, nachdem mir Dieter glaubhaft versichert hatte, daß dieser Spiegel am Himmel eine
gute Korrektur gezeigt hätte. Ich schwor mir daraufhin, mich auf solche Experimente nicht mehr einzulassen.
Zur Prüfung eines 20-inch Newton-Spiegels wäre ein Planspiegel mit einer Bohrung von 80 - 100 mm wünschenswert. Diese könnte
man nachträglich einfügen mit dem großen Risiko, daß dabei der Planspiegel in Stücke springen könnte. Um den 520 mm Flat dennoch
benutzen zu können, wäre die folgende Lösung eine Möglichkeit. Zuvor in Stichpunkten, wie man so einen Testaufbau einrichtet.
Dazu eine Grafische Übersicht , Zentrierung über Teiler-Würfel
Die Variante über die im folgenden Bild gezeigte Zentrier-Einheit funktioniert schneller und zuverlässiger, wie die weiter unten mit einem
Teilerwürfel gezeigte Lösung.

Vom 520 mm Zeiss Planspiegel links ohne Bohrung markiert das "Laser-Tool" die opt. Achse, auf die der 20-inch Newton eingerichtet wird, indem das Bündel in den Ursprung
zurück-reflektiert wird. Danach wird der Flat/Laserbündel noch ca. 8 mm in Richtung 13:00 Uhr von der Newton-Mitte verkippt. Die Rest-Koma wird über das Interferogramm
korrigiert. Dabei ist zu beachten, daß bereits die geringe Wärme des Lasers das Interferogramm beeinflußt.

Dazu wird der Laser auf Höhe gebracht von ca. 299 mm, über den Hubtisch sehr feinfühlig zu realisieren.

Anschließend setzt man vorne auf den Laser einen 10 mm Teilerwürfel, der das Laser-Bündel nach links und recht als opt. Achse darstellt. Zu dieser Achse wird nun
der Flat eingerichtet: Das in der Flat-Mitte auftreffende Bündel wird vom Flat in sich zum Teilerwürfel zurückreflektiert und der Flat sollte nun "auf der opt. Achse" sein.

Das Laserbündel tritt aber auch nach rechts in Richtung 20-inch Newtonspiegel aus, sodaß dieser zunächst auf Höhe gebracht wird und hernach durch Verkippung und
Verdrehung so zentriert wird, daß das Laserbündel nun von rechts zur Mitte des Teilerwürfels reflektiert wird. Beide Spiegel sollten nun zueinander auf der opt. Achse
liegen. Danach entfernt man diese Hilfseinrichtung wieder.

Im Bereich des Newton-Fokus liegt nun der Interferometer, der selbst zum Zeiss-Flat von einen "Arbeits-Abstand" von ca. 400 mm haben sollte. Weil aber diesmal der
Interferometer innerhalb des Strahlenganges liegt, versucht man davon möglichst wenig sichtbar zu machen; verdeckt wird dabei ähnlich viel Fläche, wie das bei einer
Bohrung der Fall wäre mit dem Vorteil, daß man von der Mitte mehr zu sehen bekommt. Das 40x6 mm Alu-Band steht als schmale Linie im Strahlengang und der untere
Kreuztisch liegt am Rande des 20-inch Newton-Spiegels.

Am oberen Teil des Alu-Bandes wird in entsprechender Höhe der Interferometer befestigt und kann nun über den Kreuztisch in alle Richtung bewegt und einge
richtet werden. Waagrechte Koma kann man am Flat mit seitlicher Verkippung korrigieren, senkrechte Koma über die Höhenverkippung des Newton-Spiegels.
Würde man nun das Kepler-Fernrohr einsetzen zur Fotografie der Interferogramme, so hätte man ein weiteres Bauteil im Strahlengang. Es empfiehlt sich deshalb,
das Interferogramm auf eine Mattscheibe zu projizieren und von der Rückseite abzufotografieren. Darunter leidet die Abbildung des Streifenbildes etwas, die
Informations selbst bleibt aber erhalten.

Bei Newton-Spiegel wird Koma grundsätzlich abgezogen und ein möglicher Restastigmatismus wird in RoC zuvor untersucht. Ist dieser zu vernachlässigen,
dann kann man diesen deaktivieren und prüft genaugenommen nur die Sphärische Aberration. Beim Rest-Astigmatismus hat man die Summe mehrerer
Ursachen: a) Einflüsse aus Schwingungen und LUftunruhe, b) Einflüsse von Hilfsoptik, c) Einflüsse aus der Lagerung der einzelnen Spiegel, und d) der
tatsächliche Rest-Astigmatismus, und nur der gehört zum Spiegel selbst. Dies klar zu trennen, dürften besonders auch den Theoretikern
schwerfallen.
Das synthetische Interferogramm bereinigt von Koma und Rest-Astigmatismus
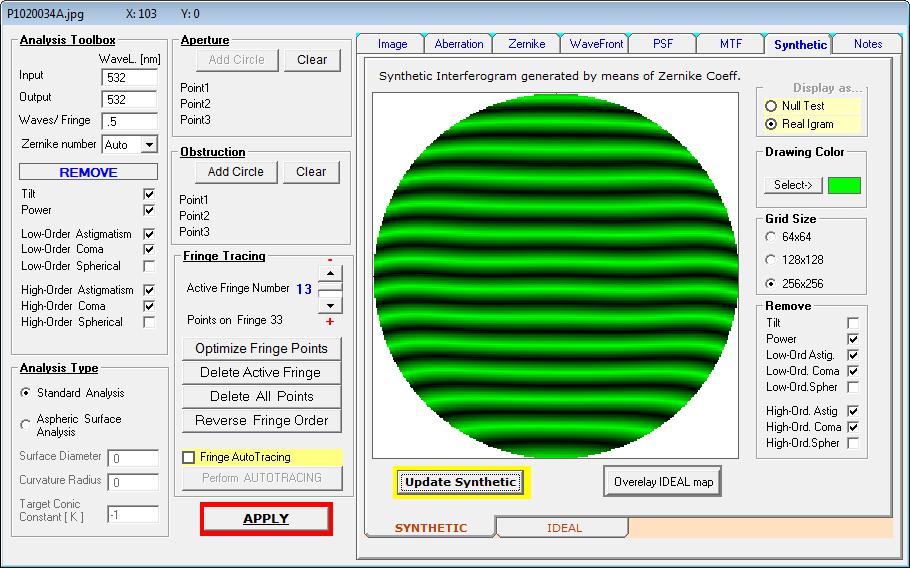
Die Wellenfront-Deformation
Die Energie-Verteilung als PSF
und schließlich das Strehlergebnis für die sphärische Aberration, was soviel heißt, daß die Spiegel-Korrektur als fast perfekte Parabel stimmt.

... und weil die Vermessung eines 20-inch Newton-Spiegels nicht so häufig vorkommt, ist dieser Vorgang als Bericht festgehalten.
X_Kap05
Ältere Bericht auf rohr.aiax.de
E001 * Übersicht einzelner Prüfverfahren auf http://rohr.aiax.de/hp_new/
E002 * Der Stern- / Artificial Sky Test - Sammung und Übersicht von Beiträgen ~.de>Link
E003 * Der Foucault-Test Sammlung und Übersicht von Beiträgen ~.de>Link
E004 * Der Ronchi-Test - Sammlung und Übersicht von Beiträgen ~.de>Link
E005 * Begriffe beim Vermessen von Optiken ,~.de>Link Definitions-Helligkeit, beugungsbegrenzt, Zit. Laux,Roger Ceragioli, Otterstedt u.a.
E006 * Der Unfug mit dem Polychromatischen Strehl , E006A Oberfläche oder Wellenfront - meßtechnisches Problem
E007 * Fraunhofer'sche Spektral-Linien im sichtbaren Teil des Spektrums, Tafel A, Tafel B, Tafel C
E008 * BasicWavefront ...save Seite 36, Bildfehler, Zernike-Darstellung u.a.
E009 * The Dall-Null-Test, der Ross-Null-Test, (Spiegel-Test-Verfahren+Ross-0-Test)
E010 * Parabel-Kompensation über Kugelspiegel oder Sphäre
E011 * Caustik-Test Links und Literatur
E012 * Night Sky 4/2003 "Klassische Optik Mythen" von Christian Losch Seite 17-25 ,
E013 * Strehl-Begriff und info1, info2, info3, info 4, E013B praxis-ferne Strehl-Diskussion/Einflußgrößen,
E013A * @immer wieder Strehl Begriff, (Rauhheit, Transmission, Reflektivität )
E014 * http://www.otterstedt.de/wiki/index.php/Strehl_Ratio
E015 * http://en.wikipedia.org/wiki/Strehl_ratio
E016 * Paranal:Strehl_Value ParanalLink1, ParanalLink2, Adaptive optics with a Laser For Astronomy
E017 * Strehlwert und Obstruktion - Modulationsübertragungsfunktion, Wie liest man MTF Kurven , Kontrast KS
E018 * Modulationsübertragungsfunktion: (Save)
E019 * http://rohr.aiax.de/Bewertung_7_Guetekriterien[1].pdf, Hofbauer Gesamtkatalog
E020 * @ Strehlsche Definitions-Helligkeit TU-Ilmenau überkorr Newton-Spiegel + PSF + Koma + Astigmatismus
E021 * Speckle-Interferometrie KLB 100923 (1).pdf
E022 * Sterntest bei obstruierten (perfekten) Systemen
E023 * Roland Christen zum Star-Test bei Maksutov-Systemen
E024 * Ein visuelles Sterninterferometer im Eigenbau Uni Wien SuW 1999 Fizeau Interferometer
E025 * Visuelles Stern Interferometer - Simulation am Kugelspiegel, Sphäre
E026 * Zentrieren oder kollimieren? Koma-/Astigm-Figuren im Bildfeld
E027 * Zentrier-Schritte eines Refraktors vor dem Planspiegel/Flat, Kollimation, Align
E028 * Stoffies Interferometer Zentrieren-Kollimieren FunktionsWeise IMeter
E029 * Test-Anordnungen RoC, Autokollimation, Planflächen, Setup, ~.deLink=>Parabel-Kompensation /E010
E030 * Aligning a Cassegrain System in front of a Flat Cassegrain, Zentrierung, Setup,
E031 * ZweispiegelSystem Zentrierung PrimärSpiegel auf opt. Achse; Fortsetzung E030
E032 * Howie Glatters Laser Collimator
E033 * Howie Glatter Laser Collimator, http://legault.perso.sfr.fr/collim.html
E034 * Howie Glatter TuBLUG 2" Newtonian Laser Collimator , Great Red Spot Astronomy Products ,
E035 * HOTECH: Zentrierung von SC-Systemen SC http://www.hotechusa.com/category-s/23.htm, E035B Bericht: Hotech Laser Collimator
E036 * APQ 110/840 Verkippung erzeugt Astigmatismus
E037 * TOA 130/1000 Verkippung erzeugt Koma+Astigmatismus
E038 * Newton-Spiegel: Verkippung simuliert mit ZEMAX <=~.Link, Autokollimations-Setup mit Planspiegelverkippung
E039 * RossNull Kompensation versus RoC, Link_01, http://rohr.aiax.de/@RC_07.jpg
E040 * http://rohr.aiax.de/@Reits05.jpg http://rohr.aiax.de/@Reits06.jpg
E041 * Link04, http://rohr.aiax.de/@Hubble08Op01.jpg Link05, Link_B ,
E042 * Test im einfachen Durchgang mit einem Newton-Spiegel
E043 * Rayleight-Water-Test Pent14\250-FlatNeuM
E044 * Elliptische Flats / Planspiegel testen
E045 * elliptischer Planspiegel (Fangspiegel) 170 mm kleine Achse Test gegen Sphäre/Kugel http://web.quick.cz/atc-astro/
E045A * Fangspiegel testen verschiedene Setups
E046 * Oldham Spiegel Rayleight Water Test
E047 * Kompensation durch Linse und Sphäre
E048 * Scopos_II: Unter- bzw. Überkorrektur bei Interferogrammen oder Wellenfront-Darstellung
E049 * Spiegel-Rauhheit im Vergleich - Übersicht von Newton-Spiegeln (etwas weniger bei =>C003)
E050 * Rauheit, Foucault, Lyot, Streulicht - Diskussion mit Dr. Weischer
E051 * Rauheit nützliche Links: Link_A , Link_B , Link_C, Link_D, Link_E,
E052 * Measurement of Surface Quality 1. Lyot Test 2. FECO 3. Nomarski Interferometer 4. Phase-Shifting Interference Microscope
E053 * Lyot-Test (Texereau, Malacara) Quellen
E054 * Jean Texereau Micromammelonnage OrginalSchrift MärzApril 1950
E055 * Lyot Test with a thin soot filter line
E056 * mein eigener Lyot-Testaufbau mit Filmnegativ Filterlinien TP 2415
E055A * E056A Micromamelonnage Diskussion auf astro-foren
E057 * Vertikaler Sterntest bei 20 inch Spiegel - Astigmatismus
E058 * LZOS Vakuum Meßturm senkrecht Sicherung auf http://rohr.aiax.de/LZOS.mht
E059 * Sterntest - gesammelte fotografische Beispiele aus Berichten
E060 * Sterntest bei obstruierten (perfekten) Systemen
E061 * Sterntest: Kommentar zu Suiter, differenzierte Anwendung/PinholeGröße
E062 * ZEMAX-Spot-Diagramme bei f/4 Newton und f/10 APO
E063 * http://rohr.aiax.de/@overcorrected.jpg Überkorrektur am Sternscheibchen
E064 * Newton 270mm f/8 Sterntest - Simulation mit ZEMAX
E065 * Telescope Optics Rutten-Venrooij
E066 * Erfahrungen mit OpenFringe Liste der Bugs
E067 * OpenFringe: Link der Zip-Datei hier zu finden , Link1
E068 * Bildfeld Radius messen, Bildfeld , 20 mm Abstand, FoucaultTest, E068C Bildfeld Radius messen - leider nicht ganz exakt !
E069 * Zeiss Plan-Werkstattspiegel Nr. 22
E070 * Dem Lutz Bath gewidmet Planspiegel-Test, f/12 Achromat älterer Bauart, Planplatte 165 mm Durchmesser, Flat 165 mm
E071 * http://rohr.aiax.de/@ReferenzSpiegel.png Verzeichnisse meiner Referenz-Sphären
E072 * Flat 10 Inch prüfen über einen 150/600 Kugelspiegel
E073 * Wie genau kann man messen? Abweichung über Koma bei Newton-Spiegel
E074 * Wider alle opt. Vernunft - Petzval-Systeme Abstand Objektiv - Reducer einhalten
E073 Wie genau kann man messen
Wie genau man messen kann, beantwortet ein Feinoptiker aus seiner langen Berufserfahrung mit Sicherheit vorsichtiger, als mancher
User, der seine Freude an spitzfindigen Haarspaltereien hat. Es artet in Rechthaberei aus, ohne besonderen Informations-Gewinn. Mit dieser
Einstellung werden hohe PV- und Strehlwerte prinzipiell als "geschönt" in Zweifel gezogen, ohne daß eine gründliche Analyse versucht
wird, welche Einflußfaktoren eine Messung beeinflussen können: Einem Feinoptiker wird man das nicht erklären müssen.
Das folgende Testergebnis entstand vor zwei Jahren und fand, wie sollte es anders sein, seinen Niederschlag in Form der üblichen
einseitigen und besser wissenden Kommentare: Die nie Gefahr laufen, sich mit den einzelnen Einflußfaktoren befassen zu müssen.
Es waren fünf Newton-Spiegel zu prüfen, zwei 8-Zöller und drei 6-Zöller mit bemerkens-wert langer Brennweite und demzufolge kleiner Öffnung.
Für derartige Spiegel ist die Autokollimations-Messung nicht anwendbar, wenn man nicht gerade einen Planspiegel mit einer 30 mm Bohrung hat,
damit abzüglich der Obstruktion durch die Bohrung noch genügend Fläche zum Messen verbleibt. Bei einem 8-inch Newtonspiegel bleibt wenig
Fläche übrig, wenn der Planspiegel z.B. 80 mm Bohrungsdurchmesser hat. Bei einer solchen Messung käme als Einflußfaktor auch noch die Genauigkeit
des Planspiegels hinzu, sowie dessen Lagerung.

Gemessen wurde also im Krümmungsmittelpunkt der Parabel (RoC genannt) Da hat man die ganze Fläche, und man sieht es daran, daß auf den Interfero-
grammen keine Bohrungen zu sehen ist. Bei den fünf Spiegeln entstanden also über dieses RoC-Setup höchst unterschiedliche Ergebnisse, aber auch das
Spitzenergebnis. (Und so ein Spitzenergebnis kann ja gar nicht stimmen, besonders, wenn es ein anderer gemessen hat :whistling) Bei diesem Spiegel Nr. 5
haben wir es mit einer ganz kleinen Öffnung von f/9.75 zu tun und in RoC wäre das zu verdoppeln mit R/19.50. Das ist also ein sehr schlanker Lichtkegel
mit 173 mm Durchmesser und 3374 Länge bzw. Radius.
Jeder wird wissen, daß bei einer solch langen Wegstrecke sehr viel Luftbewegung im Spiel ist, was die Messung, und im konkreten Fall den gemessenen
Astigmatismus erheblich beeinflusst. Beim Messen von Spiegel hat man es mit mehreren Ursachen von Astigmatismus zu tun: Lagerungs-A, Luft-Turbulenz-A
und spiegeleigener Astigmatismus. Nicht ohne Grund hat LZOS einen senkrechten Vakuum-Meßturm, der solche Einflüsse minimiert.
LZOS Vakuum Meßturm senkrecht
Es war also der Spiegel Nr. 5, (ausgerechnet der Beste eben) dessen hohe Qualität ohne Grund erst einmal angezweifelt wurde, prinzipielle Argumente,
die immer angeführt werden, wenn man keine belastbaren Fakten hat.

Selbst bei einem RoC-Setup ist bei einem so langen Radius von 3374 mm die Luftbewegung nicht zu unterschätzen, sodaß ich zu Beginn zunächst
einen Astigmatismus-Ausschluß-Test durchführe. Nach der Zernike Tabelle gibt es mehrere Formen von Astigmatismus, wobei die Grundform in
der Regel diejenige ist, die ab allerhöchstens PV L/5 bei hohen Vergrößerungen überhaupt wahrgenommen wird. Ohne also beim Strehl-Wert
anteilig die jeweiligen Fehler zu betrachten ist ein isolierter Strehlwert eine schiefe Information. Man wird sich also vergewissern, ob man einen
signifikanten wahrnehmbaren Astigmatismus vor sich hat, der entsprechend berücksichtigt werden muß, oder nicht. Das folgende IGramm läßt
nur den Schluß zu, daß kein signifikanter Astigmatismus der Grundordnung im Spiel ist. @ Der Zernike Zoo Im Falle zweier anderer Spiegel
sieht das dann so aus: http://rohr.aiax.de/L5M_03A.jpg
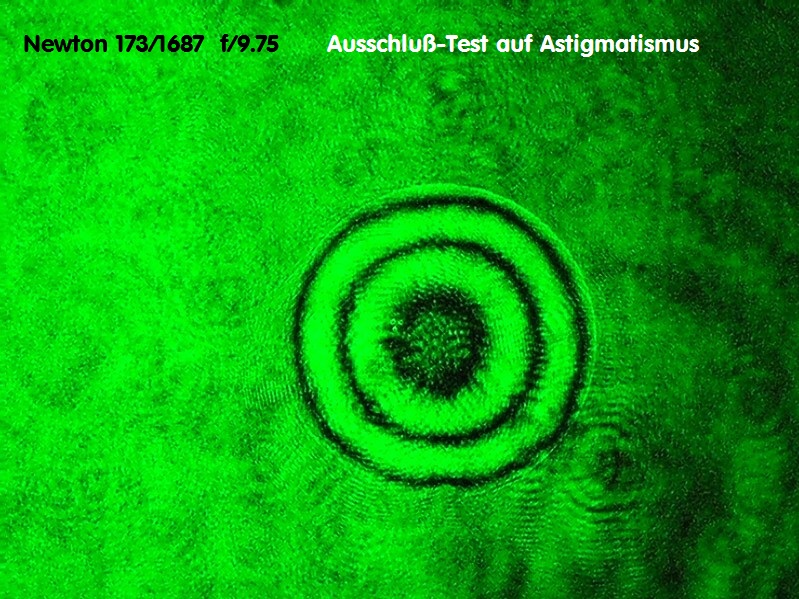
Man kann den Sachverhalt von einer anderen Seite betrachten:Es ist allgemeiner Konsens, daß man bei der Streifenauswertung Koma abziehen darf, mit dem
Argument, daß eine Parabel auf der Achse keine Koma haben kann. Damit wird aber zugleich bestätigt, daß Interferogramme trotzdem Koma enthalten, die das
Ergebnis unberechtigterweise verfälschen. Bei diesem Spiegel würde der Wert für die Koma den Strehl auf 0.961 drücken bzw. ein PV-Wert von L/7.6. Auch
die Koma ist u.a. ein Ergebnis von Seeing-Effekte und Testaufbau zwischen Lichtquelle und Spiegelfläche. Während also bei der Koma keine prinzipiellen Diskus-
sionen vom Zaun gebrochen werden, verbleibt der Low- und High-Order Astigmatismus ohne größere Differenzierung in der Diskussion. Natürlich auch Low- und
High-Order Spherical. Die Feinheiten einer Messung in Roc bleibt bei der üblichen Pauschal-Beurteilung ebenfalls "außen vor". Obwohl also die gezeigte Koma und
ihr Strehlwert im Interferogramm stecken, bleibt dieser Wert aus den bekannten Gründen unberücksichtigt. Siehe auch: http://rohr.aiax.de/L5M_08A.jpg
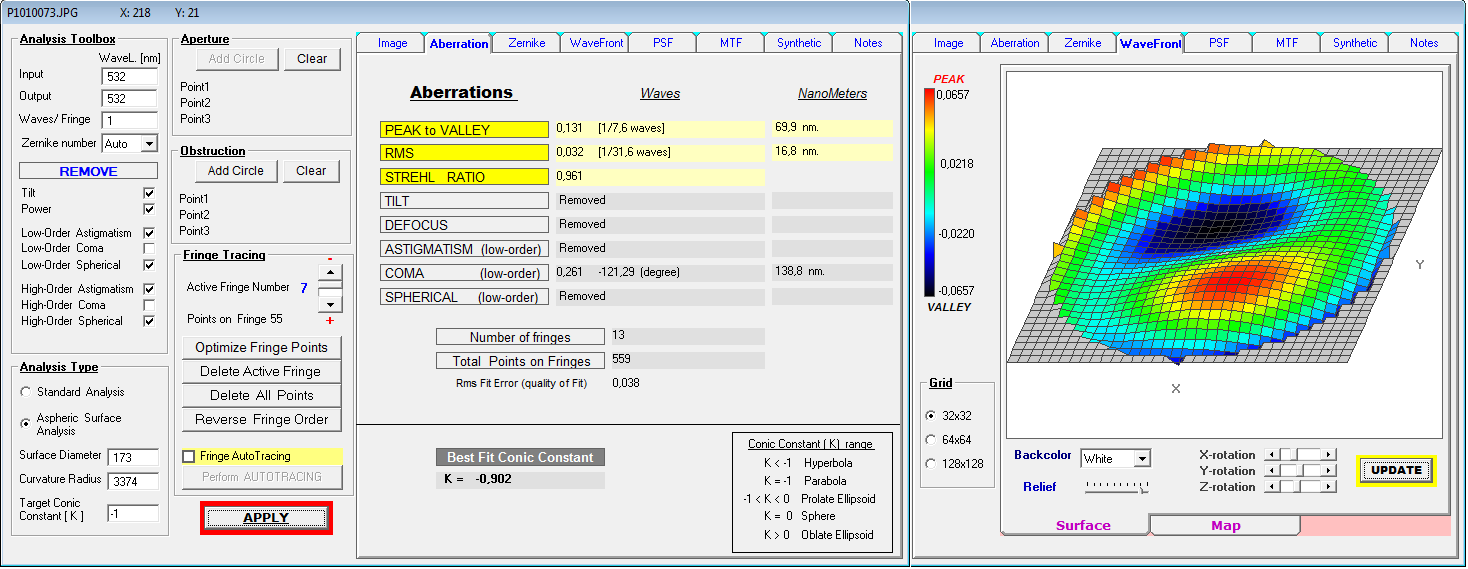
Bei einem RoC-IGramm eines f/10 Newtonspiegels ist der Unterschied zur Sphäre bzw. Kugel nicht mehr groß. Und trotzdem ist die Überkorrektur
aus Sicht der Kugelmessung noch eindeutig feststellbar: Die Streifen sind "M"-förmig gebogen und werden als RoC-IGramm ausgewertet bzw. im Null-
Testverfahren umgerechnet.

Zum damaligen Zeitpunkt hatte ich zwei Igramme ausgewertet und danach das "schlechtere" Strehl-Ergebnis weitergegeben. Das bessere liegt sogar bei 0.999
Strehl - das muß doch geschönt sein !??? :whistling In endlosen Meßreihen - ein Feinoptiker hätte schon längst mit dem Kopf geschüttelt - kämen dann gemittelte
Ergebnisse heraus, ohne die grundsätzliche Sicherheit, ob so ein Verfahren genauer und richtiger sei, und ohne die grundsätzliche Frage, wieviel Strehl braucht
das spätere Teleskop überhaupt im Praxisbetrieb und wieviel davon läßt sich auf der Basis der Bauweise und der Standortbedingungen realisieren.
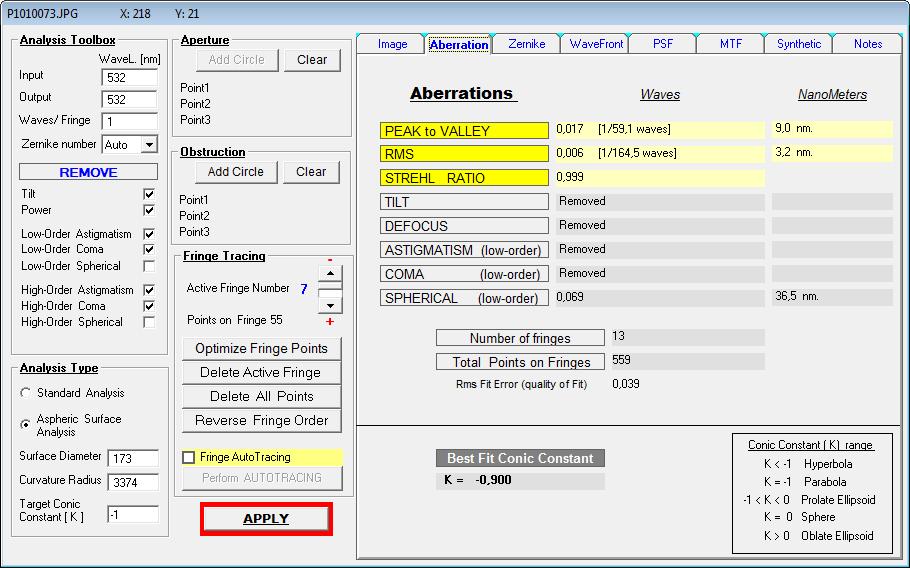
Das RoC-IGramm wurde also auf Null zurückgerechnet, wie es z.B. der ZYGO macht, und dadurch entsteht in diesem Fall eine perfekte PSF-Verteilung.
Die deswegen in der Praxis nicht stimmt, weil der Fangspiegel ohnehin das System obstruiert.
Das obere reale RoC-Igramm läßt sich also auf Null-zurückrechnen, und bei einem hochwertigen Spiegel entstehen dadurch absolut gerade Streifen.
Weil also dieser beste Spiegel unter fünf Spiegeln seinen Weg zum Kunden gefunden hat, ist das noch lange kein Grund, ein so erfreuliches Ergebnis
als "geschönt" zu verurteilen, nur weil man es nicht selbst gemessen hat.
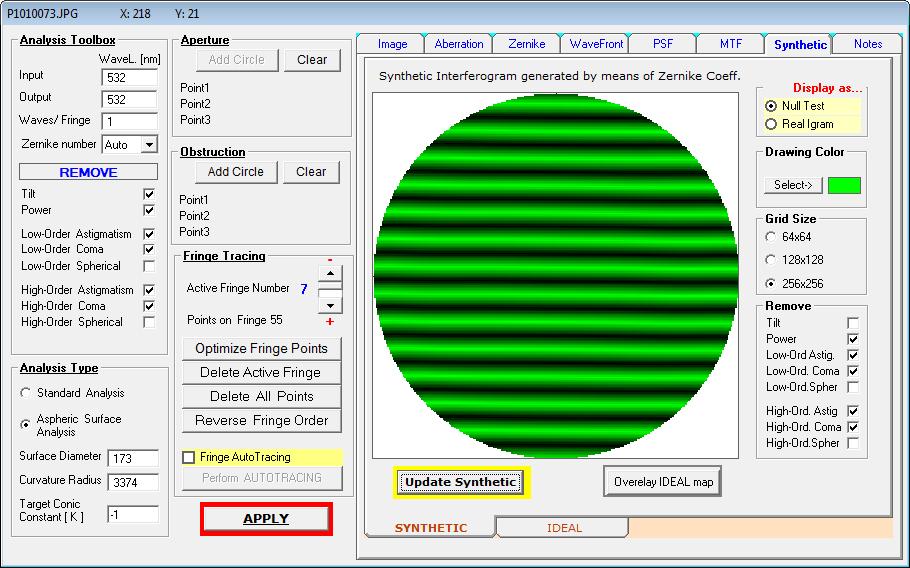
E070 Dem Lutz Bath gewidmet Planspiegel-Test
Dem Lutz Bath gewidmet
Sie liegen schon eine Weile bei mir, die beiden Teile: Von Eugen Aeppli stammt der Planspiegel mit Durchmesser 200 aus Quarz, den Lutz Bath
gerne verkauft hätte und deshalb gern wissen möchte, wie genau dieser ist. Das zweite Objekt ist ein sehr betagtes Objektiv mit Messing-
Fassung, ein sehr guter Achromat an der Grenze zum Halb-APO. Durch das Öffnungsverhältnis von ca. f/12 konnte man auch schon vor Jahr-
zehnten sehr farbreine Objektive mit zwei Linsen herstellen.
A: der Aeppli Planspiegel
Eugen Aeppli, damals von Beruf Busfahrer, habe ich Mitte der 70-er Jahre des letzten Jahrhunderts ein paarmal besucht. Er war damals eine bekannte Größe
auf dem Gebiet des Spiegelschliffs und wird erwähnt im Buch von Hans Rohr, "Das Fernrohr für Jedermann" Orell Füssli Verlag Zürich, 5. Auflage S 177. Aeppli
schliff u.a. ein 80 cm RC-System für einen betuchten Sternfreund südlich von Frybourg, den ich ebenfalls zweimal aufsuchte. Danach hatte Aeppli eine Zeitlang
eine Meade-Vertretung und soll später in die Türkei übergesiedelt sein. Das ist schon ca. 35 Jahre her.
Von ihm stammt also dieser Planspiegel. Bei Planspiegeln kommt es sehr darauf an, wie er verwendet wird, da auch Planspiegel eine Reihe von Fehlern haben können.
Da wäre zunächst die Frage nach der Planität oder auch Power genannt. Solange man einen solchen Spiegel in einem Autokollimations-Setup verwendet, spielt
selbst ein Krümmungsradius von ein paar Kilometer noch keine Rolle. Wichtiger wäre die Regelmäßigkeit des Spiegels: Er sollte also möglichst keine deutliche Zonen
haben. Der dritte Schönheitsfehler wäre eine abgesunkene Kante, die lediglich den verwendbaren Durchmesser etwas einschränkt. In unserem Fall hätte dieser
Spiegel bei 165 mm Durchmesser einen Strehl von 0.993 oder einen PV-Wert von Lambda/14.2 - bezogen auf die Regelmäßigkeit. Damit wäre dieser Planspiegel
gut als Kollimations-Spiegel für alle Refraktor-Optiken verwendbar, die selten über 150 mm Durchmesser hinausgehen.
Das erste Bild zeigt den Spiegel in einem Setup mit einem Kugelspiegel 250 R 2368 und bedeutet, daß die Planfläche mit doppelter Genauigkeit gegen die Sphäre
geprüft wird.

Der einfachste Test wäre ein Test auf Kontakt gegen eine bekannt gute Planplatte mit Zertifikat. Da aber der Aeppli-Planspiegel bereits belegt ist, sind die
Interferenz-Streifen kontrast-arm, wie das spätere Foto beweist. Aber es wäre ein Prüfverfahren, bei dem alle Fehler zu sehen sind: Also Power, Regelmäßigkeit,
abgesunkene Kante, eventuell Astigmatismus.
.

Meine Referenz-Planplatte wurde 1995 von Peter Rucks über einen Zygo vermessen mit den folgenden Ergebnissen. Leider hat er damals die Power nicht eigens
ausgewiesen. Auch bin ich im Zweifel, ob der Scale-Wert von 0.5 stimmt, den man nur bei einer Prüfung gegen einen Kugelspiegel so einsetzen dürfte. Es ist
eher anzunehmen, daß ein Referenz-Objektiv im Spiel war, und da passiert das Licht die geprüfte Oberfläche nur 1x .
.
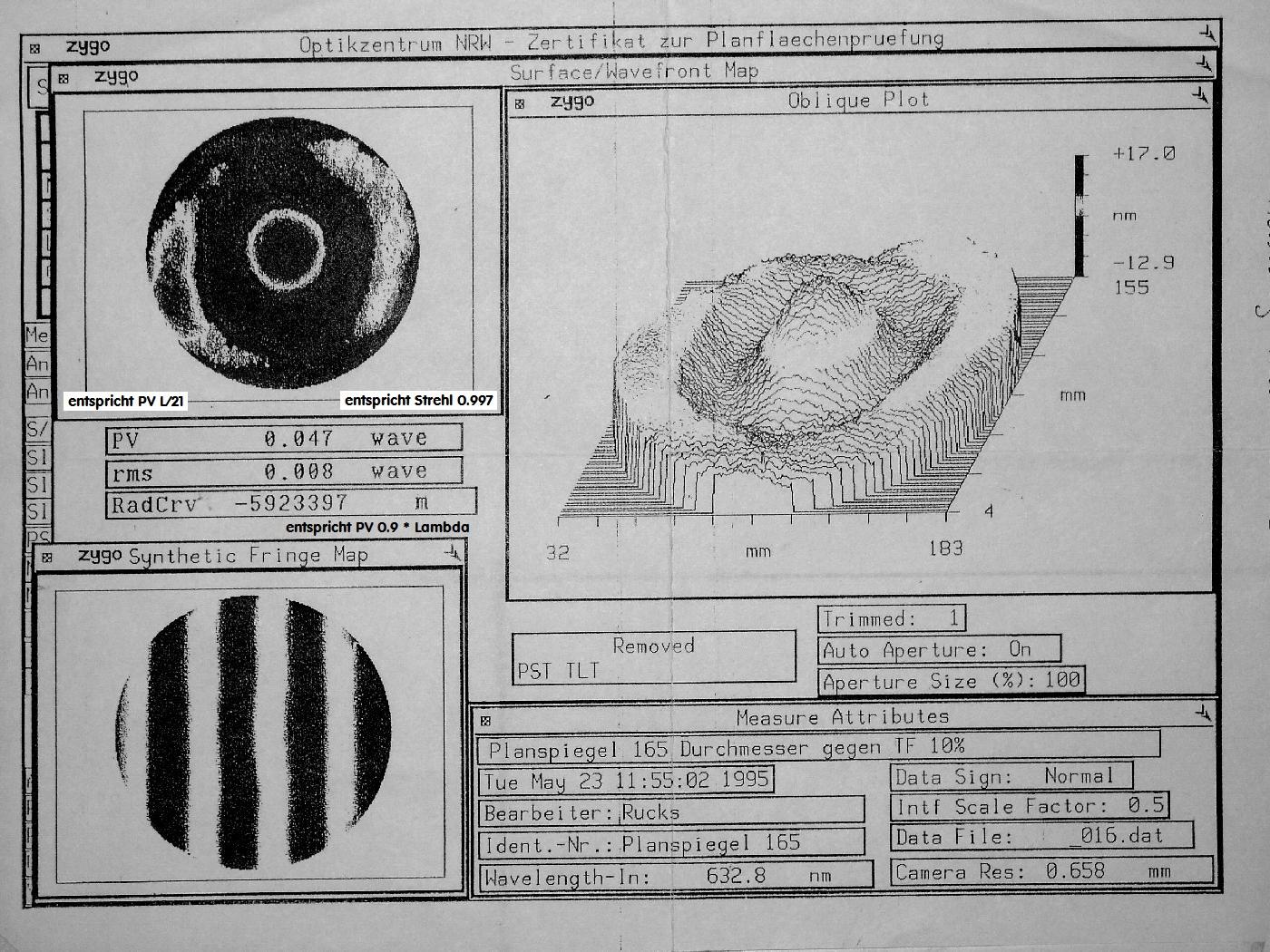
Unter einer Natrium-Dampflampe entstand bei 587.6 nm wave auf Kontakt dieses Interferogramm, dessen Streifendurchbiegung auf eine Power von ca. 1 x Lambda
hinweisen, was für einen Kollimations-Spiegel keinen Einfluß hat. Auch in einem Teleskop wäre er einsetzbar, solange das Lichtbündel nahezu senkrecht einfällt.
Unter diesen Bedingungen bei Durchmesser 165 bekommt man also bei einfachem Durchgang einen Strehl von 0.993 oder PV L/14.2 .
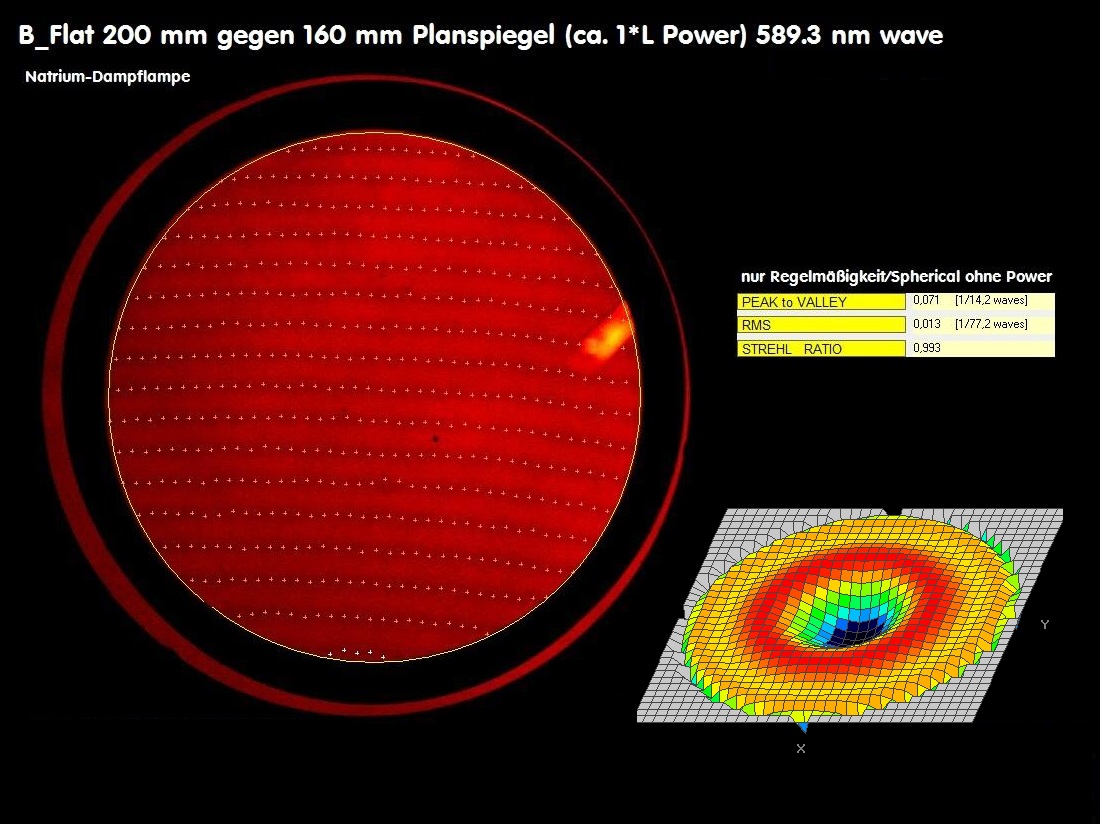
Beim Test gegen einen Kugelspiegel, in meinem Fall 255 R 2368 muß man natürlich auch die Genauigkeit der Sphäre wissen, weshalb beide Fläche im Foucault-Test
nebeneinandergestellt werden. Die über den Foucault-Test erkennbaren Unterschiede sind nicht mehr deutlich sichtbar.
Als auffälligstes Merkmal ist beim Ronchi-Test die abgesunkene Kante des Planspiegels erkennbar. Die Regelmäßigkeit der Fläche bzw. die sphärische Aberration
ist nahezu perfekt.

Auch beim Streifenbild fällt wieder die abgesunkene Kante auf, innerhalb derer der Planspiegel aber gut verwendbar ist. Ohne diese wäre der PV-Wert bei ca. L/12
und liegt ziemlich deutlich in der Gegend der 1. Messung mit der 165 mm Planplatte. Dazu wieder im Vergleich die Referenz-Sphäre selbst, deren PV-Wert bei ca. L/9 liegt. Man kann also davon ausgehen, daß der Aeppli-Planspiegel bei PV L/10 der Wellenfront liegt oder bei PV L/10 der Oberfläche. Je genauer man ein Meßergebnis
haben möchte, umso aufwendiger wird die Prüfung und Rechnerei. Eugen Aeppli hat damals seine Planspiegel gegen eine 600 mm Planplatte geprüft unter einer
ultravioletten Lampe. Davon gibt es auch ein Foto.
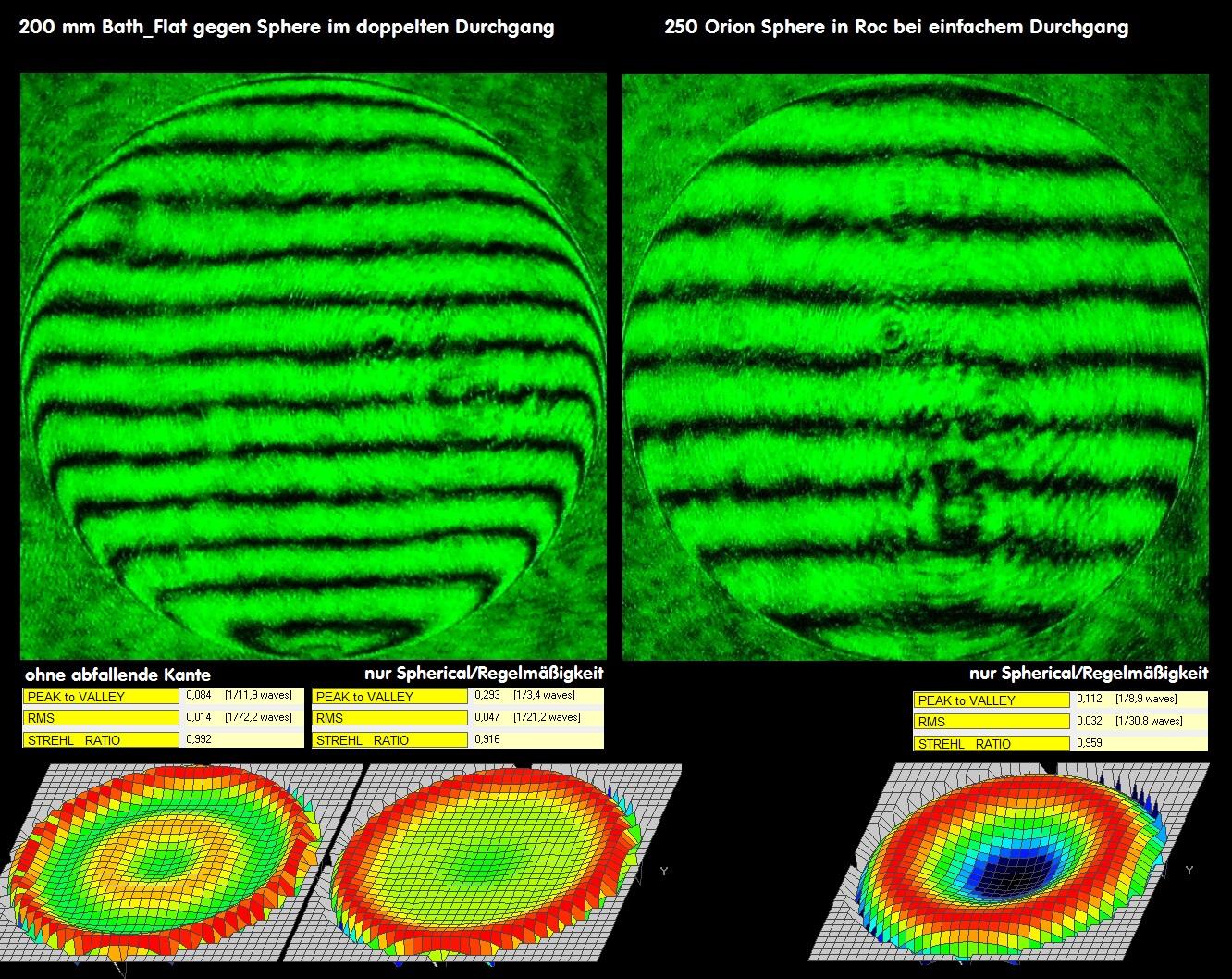
B: das 54/660 mm Objektiv
Lutz Bath "gräbt" des öfteren auch historische Objektive aus und wollte in dem Zusammenhang wissen, wie gut dieser Achromat unter heutigen Ansprüchen
eigentlich ist.

Aus der Schnittweiten-Differenz der Spektral-Farben Rot - Grün - Blau ergibt sich bei diesem f/12.222 System ein RC-Index von 2.1024, was sehr gut an
die heutige ED-Objektive heranreicht.
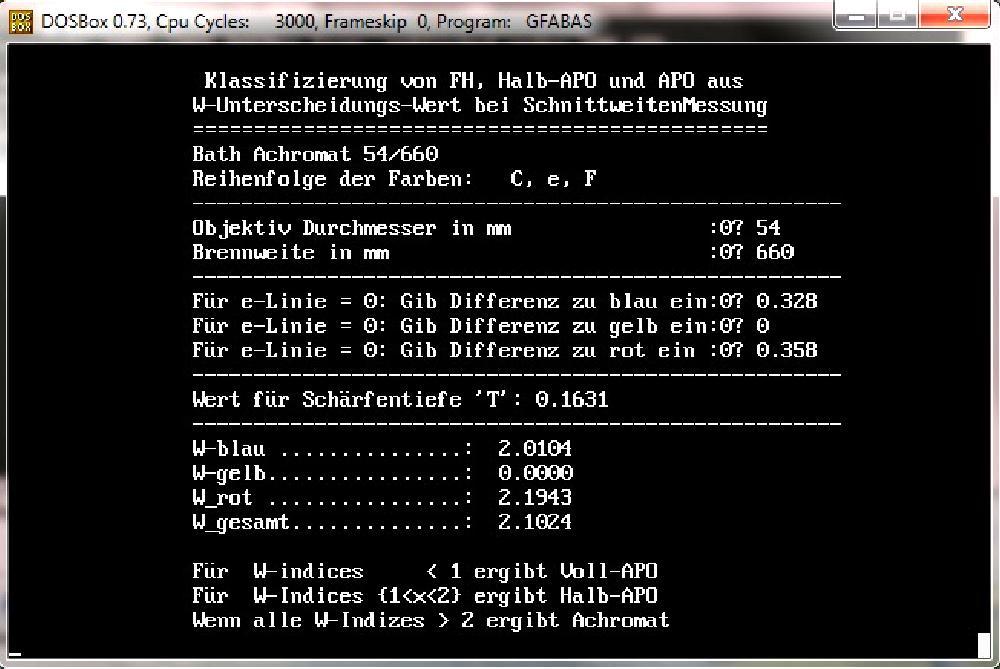
Bei der Farbverteilung des Foucault-Testes kann man ebenfalls den Achromaten erkennen. Hier spielt der Gaußfehler eine untergeordnete Rolle.
.
Aus dem Testbild des Artificial Sky Testes bei Höchstvergrößerung kann man die Auflösung berechnen, die dem theoretischen Wert sehr nahe kommt. Einen
Hinweis auf Astigmatismus enthält dieses Testbild nicht, weshalb bei der Streifenauswertung später der Astigmatismus abgezogen worden ist.
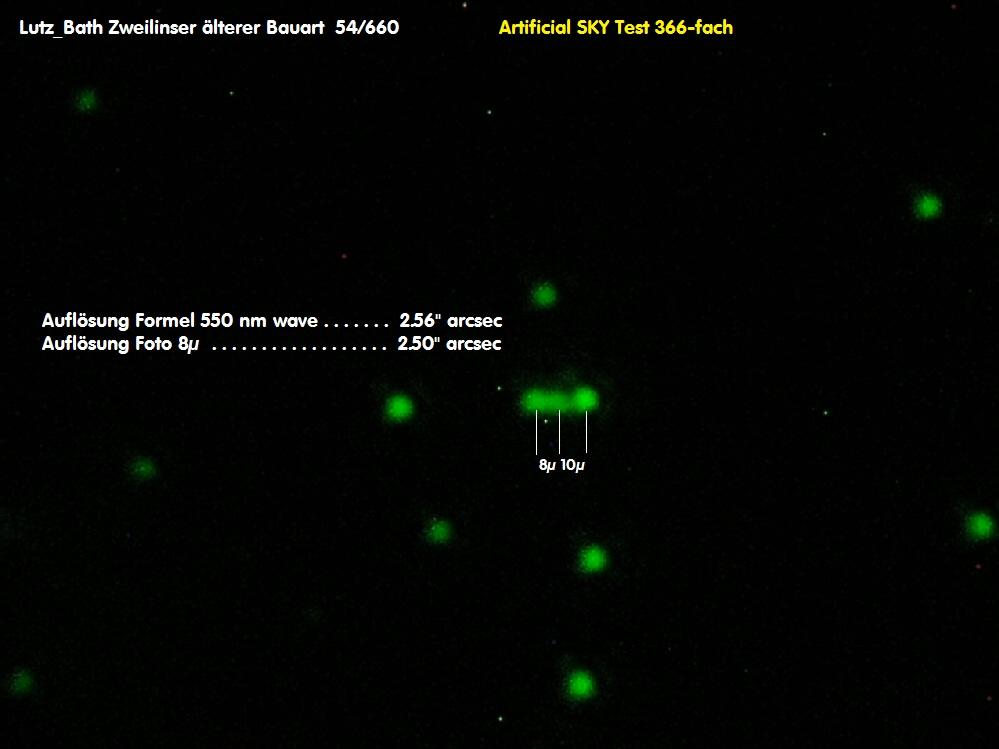
In diesem Fall könnte der erkennbare Astigmatismus über den Testaufbau eingeführt werden. Eine Entsprechung zeigt das Streifenbild auch zum
Foucault-Test, wenn man beide miteinander vergleicht.
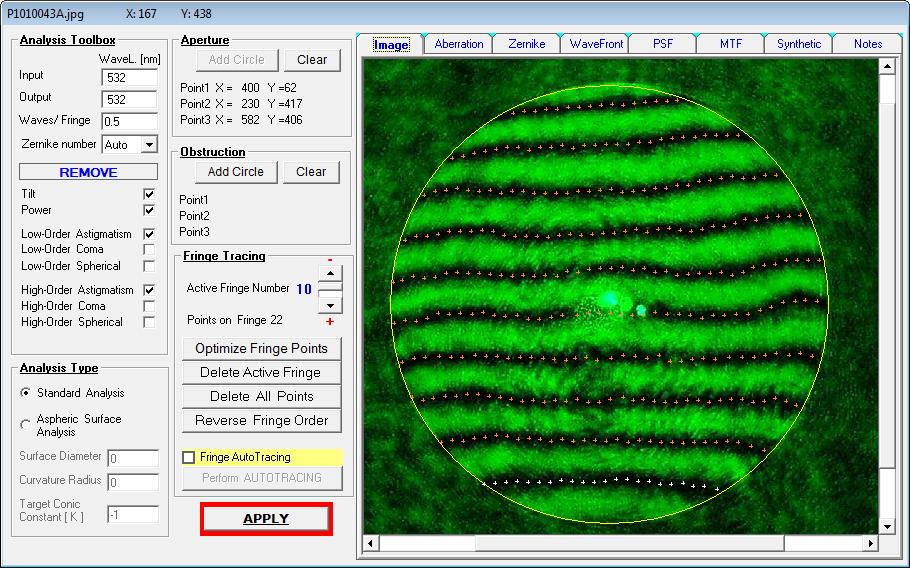
Ein Öffnungsfehler von ca. PV L/10 wird man vernachlässigen können.
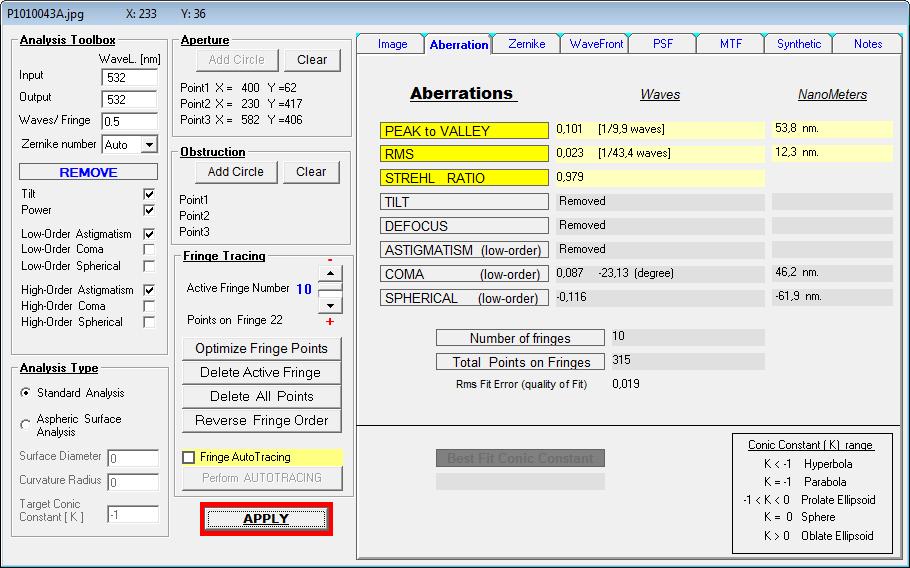
Die Wellenfront-Deformation jedenfalls wird hier überdimensioniert dargestellt, entspricht aber dem Foucault-Bild. Ob Galileo Galilei
vor 370 Jahren ein solch hervorragendes kleines Objektiv hatte?
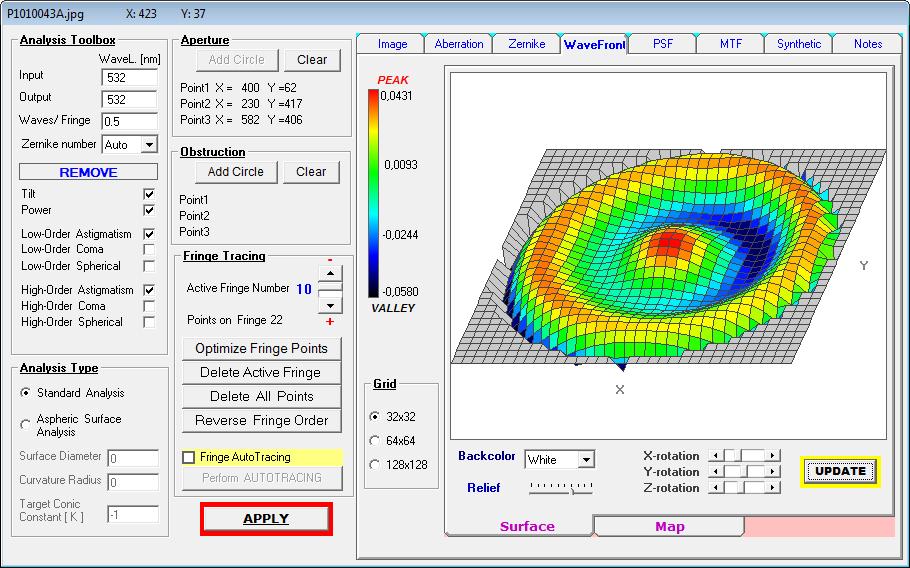
. . . . . . . . . .
E069 Zeiss Plan-Werkstattspiegel Nr 22
Zeiss Plan-Werkstattspiegel Nr. 22
Dieser 520 mm Zeiss Plan-Werkstattspiegel Nr. 22 scheint eine bewegte Vergangenheit hinter sich gebracht zu haben. Jedenfalls war er gründlich
eingestaubt, sodaß der Staub zunächst ein schlechteres Ergebnis vortäuschte. Erst eine vorsichtige Reinigung zeigte den Spiegel so, wie man ihn
von Zeiss eigentlich erwarten durfte.
Der Plan-Werkstattspiegel Nr. 22 in einem neuen Gehäuse, aufgehängt in einem Kunststoffband mit Sicherungen oben und unten.

Die Gravour auf der Rückseite verrät die Herkunft, auch wenn der Begriff "Zeiss" leider fehlt. Er muß wohl zwischendurch in einer mittlerweile aufgelösten Sternwarte
als Sonnen-Kollimationsspiegel seinen Dienst versehen haben.

Nun möchte man wissen, welche Qualität man bei diesem Planspiegel erwarten kann. Also schaut man sich die Planfläche über einen Kugelspiegel an, der zwar
eine gute Sphäre hat, aber leider keine perfekte Oberfläche. Doch davon später. Genau dieser Umstand führte einstens dazu, daß ich eine Primadonna aus der
Szene tödlich beleidigt hatte, weil mir dessen Fläche nicht genau genug war.

Die Strehlwerte dieses 250 R 2400 Kugelspiegels wären ausreichend hoch

Wobei man Koma ohnehin abziehen kann, und auch Astigmatismus mehrere Ursachen haben kann, weshalb eine Zuordnung sehr kompliziert wäre.
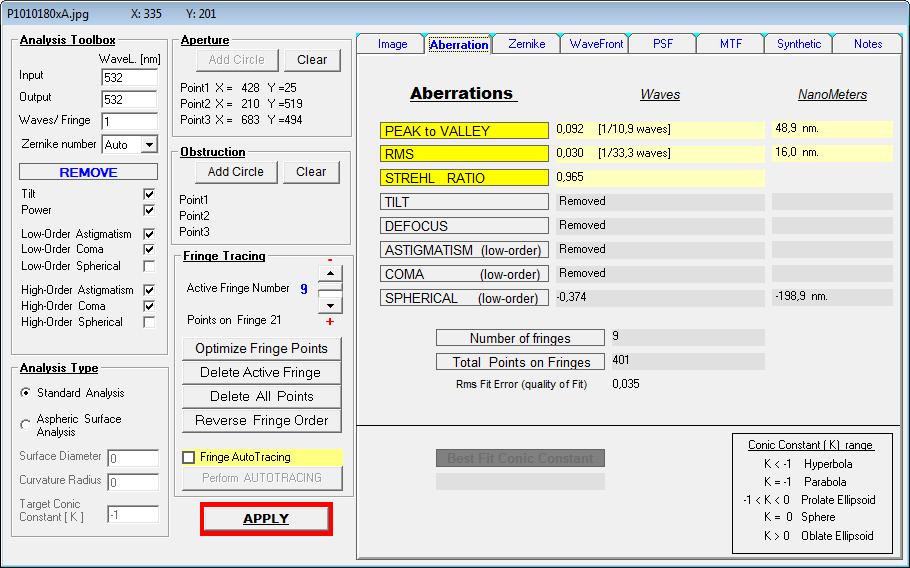
Sinnvoll ist deshalb der Vergleich des Foucault-Testes: Links im doppelten Durchgang über den 520 Zeiss-Flatt selbst und rechts der gleiche Foucault-Test
nur mit dem Kugelspiegel allein. Da sich beim Vergleich zeigt, daß die Flächenstrukturen unter Lambda/10 der Wellenfront sehr viele Ähnlichkeiten links über
den Zeiss Planspiegel haben, verglichen mit dem Foucault-Test des Kugelspiegels selbst, zeigt sich in diesem Test kaum ein Einfluß, den der Zeiss Flat auf
diesen Meßvorgang hätte. Das bedeutet, daß der Zeiss Planspiegel eine hohe Genauigkeit haben muß: Mindestens PV Lambda/10 und besser mit einer hohen
Glätte der Fläche. Damit wäre der Foucault-Test weitaus informativer als der nachfolgende Interferometer-Test.
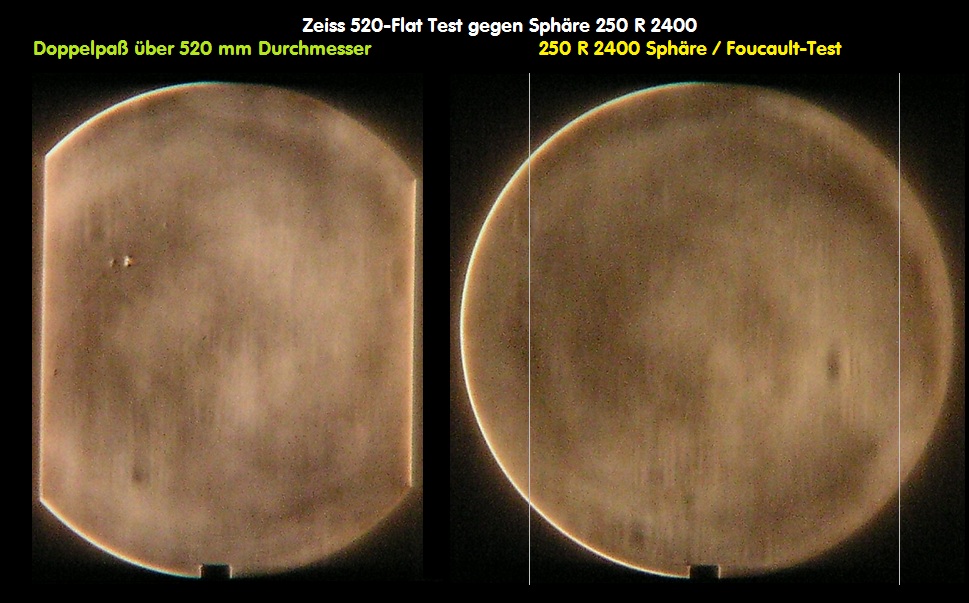
Im linken IGramm ist über den ansteigenden Streifenabstand von oben nach unten ein Astigmatismus erkennbar, der ein Hinweis auf die Planität bzw. Power wäre.
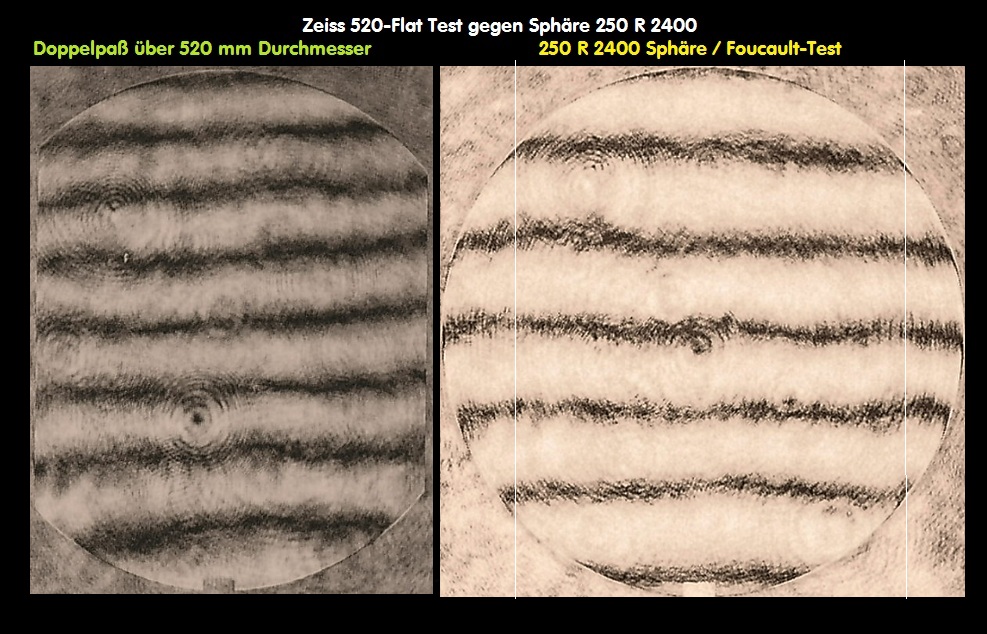
Blickt man in einem flachen Winkel über eine noch so große Sphäre, dann entstehen astigmatische Bilder, über deren Größe man auf die Pfeilhöhe des Krümmungs-
Radius schließen kann. Überschlägig im Bereich von ca. 200 km Radius.

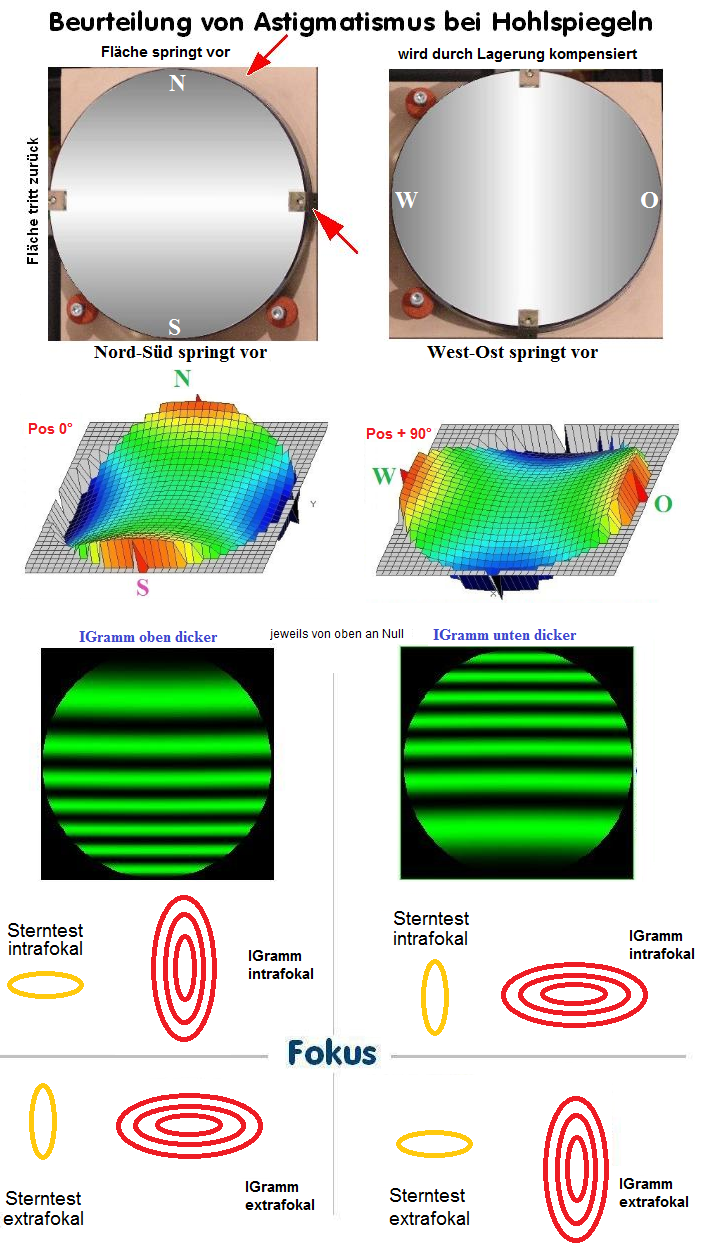
E068C Bildfeld Radius messen - leider nicht ganz exakt
Bildfeld Radius messen - leider nicht ganz exakt !
Der folgende kleine Beitrag zeigt eine nicht ganz exakte Möglichkeit, über den Foucault-Test den Bildfeld-Radius zu messen. Die "Unschärfe" entsteht auch dadurch, daß mit dem Foucault-Test der Fokus nicht ganz exakt festgelegt werden kann.

Diese Mittelung ist erforderlich, weil es zunächst unbekannt ist, ob die drei Klingen exakt im rechten Winkel zur opt. Achse stehen, dann würde die Fokus-Längen-Differenz
von linker und rechter Klinge zur mittleren Klinge übereinstimmen.
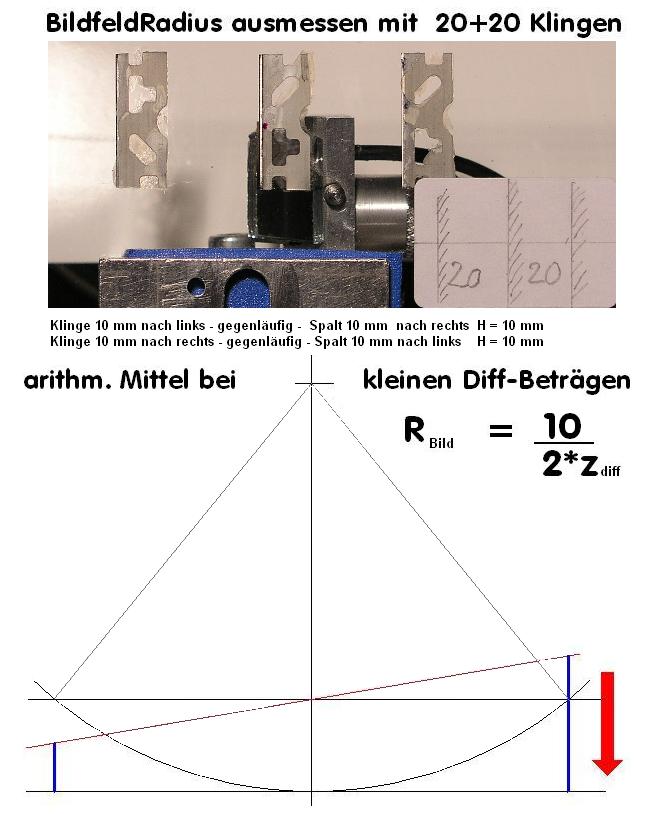
E064 Newton 270mm f8 Sterntest - Simulation mit ZEMAX
Wenn einer Spiegel schleift, im konkreten Fall mit Durchmesser 270 mm und einem Krümmungs-Radius von
4380 mm (eigene Angabe), dann schleift er zunächst die Sphäre (also den Kugel- oder Hohlspiegel) und
poliert diese aus, wobei er zunächst die Sphäre selbst mit einem künstlichen Stern als Lichtquelle und dem
Messerschneide-Test nach Foucault, also die Kugelform selbst prüft. Diesen Fall kann man auch mit ZEMAX
simulieren oder irgend einem anderen Optical Design Program. Die Conic Constant wäre in diesem Fall
= Null. Perfekt schaut dann die Sache aus, wenn der Foucault-Test einen "topf-ebene" Flächen-Eindruck
hinterläßt.
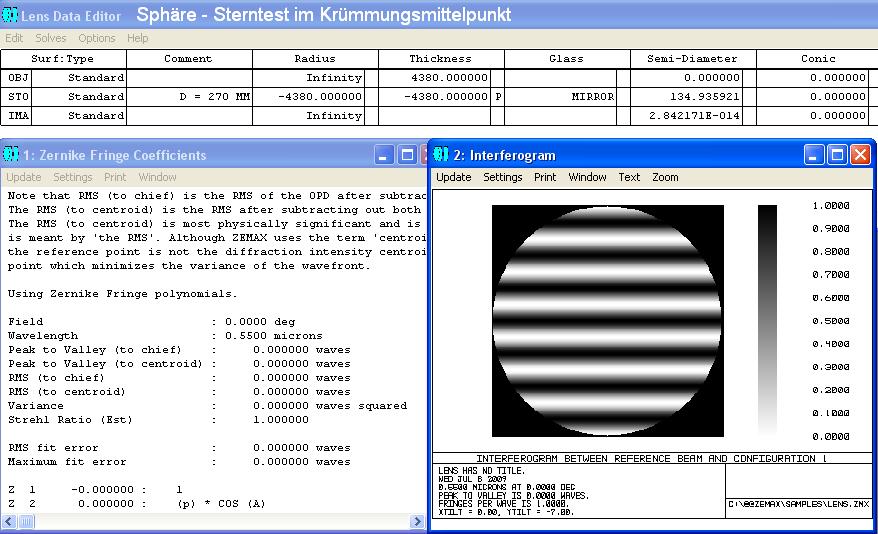
Da aber ein f/8 System wie hier am Himmel bereits ausreichend wäre, könnte man beim Erreichen der Kugel eigentlich aufhören.
Der TAL-Spiegel war so ein Beispiel. Wenn man aber eine perfekte Parabel vor sich hätte, dann bekommt man einen überkorri-
gierten Flächeneindruck, weil bei einer Parabel im Krümmungsmittelpunkt die Mitte einfach tiefer liegt, und man deswegen von
einer Überkoprrektur spricht: Es wurde zuviel wegpoliert, also überpoliert oder überkorrigiert. Der Strehl würde deswegen im
Krümmungsmittelpunkt wegen dieser Überkorrektur auf 0.50 sinken und man hätte heftige Beugungsringe um die Sterne.
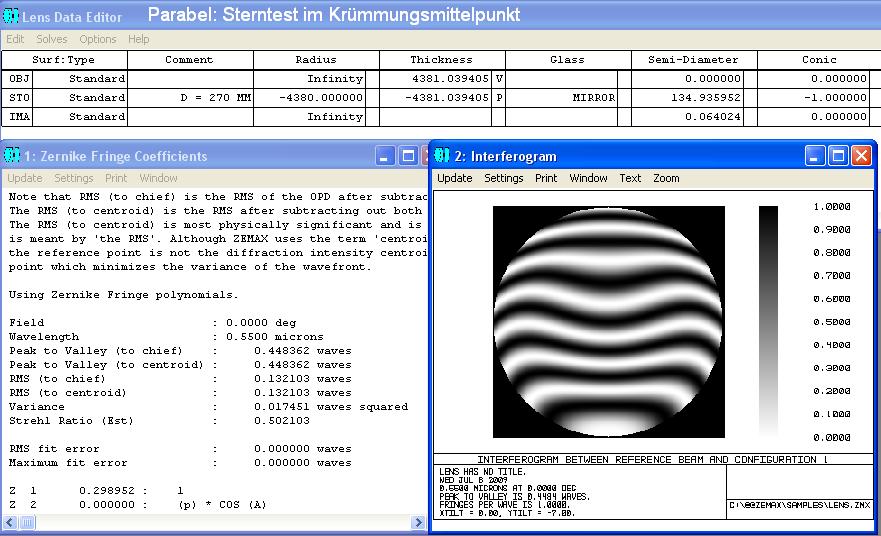
Nun kann man den Abstand des künstlichen Sternes vergrößern. Vorgeschlagen wurden 20 000 mm oder 20 m. Damit kann man
mit einer Genauigkeit von Strehl = 0.90 prüfen oder aber, wenn man wieder ganz exakt topf-eben korrigiert, hätte man eine
Ellipse mit einer conischen Konstanten von - 0.60 oder ganz einfach einen unterkorrigierten Spiegel, was bei einem f/8 System
kein Problem ist.
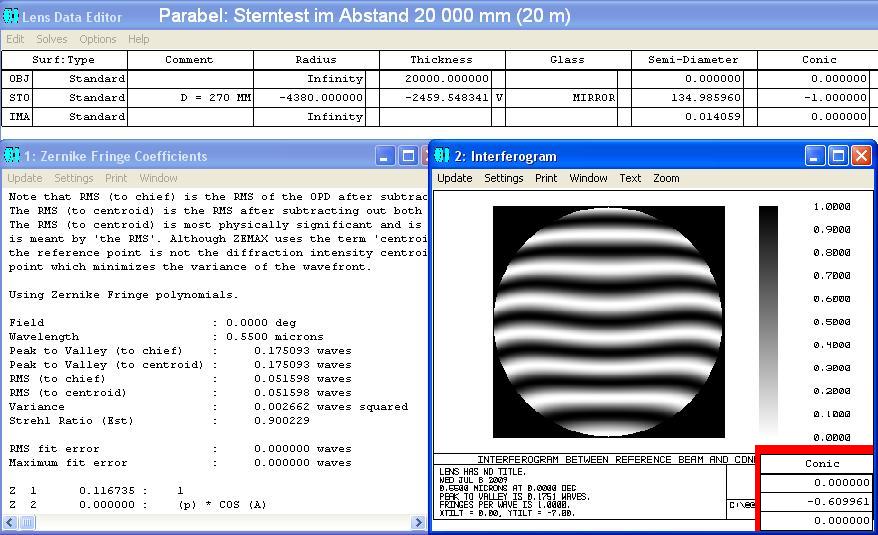
Wer die Perfektion anstrebt, sollte den künstlichen Stern in diesem Beispiel auf mindestens 40 000 mm (40 m) halten, dann
käme er in der Genauigkeit bereits auf einen Strehl von 0.97, und diese Genauigkeit zählt bereits zu den hochwertigen Spiegeln.
Sehr viel wichtiger ist außerdem die Prüfuung auf Astigmatismus, denn bereits ein Astigmatismus von nur L/4 PV zieht den
Strehl leicht um 10 - 15 Strehlpunkte nach unten und bildet sich im Fokus später als Kreuz ab. Statt den künstlichen Stern
zu benutzen, wäre der Polarstern weitaus sicherer, wenn man die exakte Parabel anstrebt. Es geht also auch recht einfach.
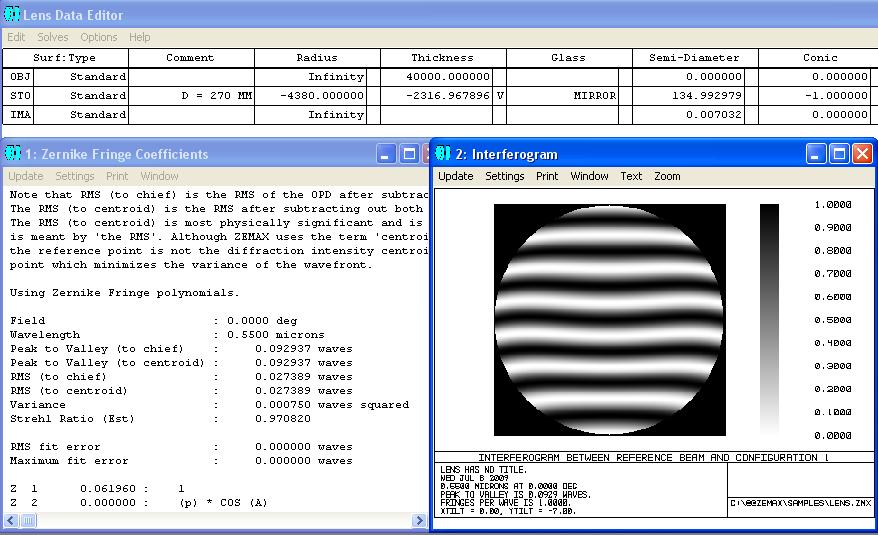
Wenn die Rückseite des Spiegels nicht gerade blank und durchsichtig ist, sondern matt geschliffen, dann lassen sich
alle wichtigen Tests durchführen. Andernfalls stören die Reflexe von der Rückseite ziemlich heftig.
E060 Sterntest bei obstruierten (perfekten) Systemen
Lieber Michael Korff-Karlewski,
mit dem Suiter Buch habe ich so meine liebe Not.
Warum?
Weil Computer-generierte Sternscheibchen-Tests höchst selten mit der viel differenzierteren Wirklichkeit
am Himmel oder auf der opt. Bank etwas zu tun haben. Dieses Buch stiftet mehr Verwirrung, als daß es
hilft, optische Fehler aufzudecken.
Für Refraktor-Optiken ist der Stern-Test nur sehr eingeschränkt verwendbar. Es fehlt die Farbinformation.
Dort wären der Farblängsfehler, fehlerhafte Zentrierung und eventuell der Gaußfehler gesondert und vor
allem farbig zu würdigen, was dieser schwarz-weiß-Test nicht hergibt. Mein Wissen um opt. Fehler beim
Sternscheibchen-Test resultieren aus den vielen praktischen Tests, aber ganz bestimmt nicht deswegen,
weil ich dem Suiter vertraue, der übrigens vor mir liegt.
Es läuft prinzipiell auf die Verabsolutierung eines einzigen Tests hinaus ohne irgend eine Gegen-
kontrolle. Und das lehne ich grundsätzlich ab. (Die meisten Händler und Sternfreunde haben in der Regel
nichts anderes zur Beurteilung, weswegen dessen Bedeutung überdimensioniert wird.)
Der Sachverhalt läßt sich ganz einfach simulieren. Ein nahezu perfekter Kugelspiegel sollte beim Sterntest
intra/extrafokal keine großen Unterschiede zeigen. Wenn man die Mitte mit einer Scheibe obstruiert, hat
man prinzipiell ein perfektes SC-, Cassegrain-, RC- oder Maksutov-System vor sich. Jeweils perfekt.
Erzeugt man mit diesem Setup die bekannten Sternscheibchen, bekommt man dieses Ergebnis, was ich so
interpretiere, daß keine signifikanten Unterschiede erkennbar sind. Alles andere wäre Kaffeesatz-Leserei.
Siehe auch hier:
http://www.astro-foren.de/showpost.php?p=34661&postcount=2
Je größer die Obstruktion, umso mehr Energie verlagert sich in die BeugungsRinge. Das wäre der einzige
Effekt, der sich auf die Sternscheibchen auswirkt.
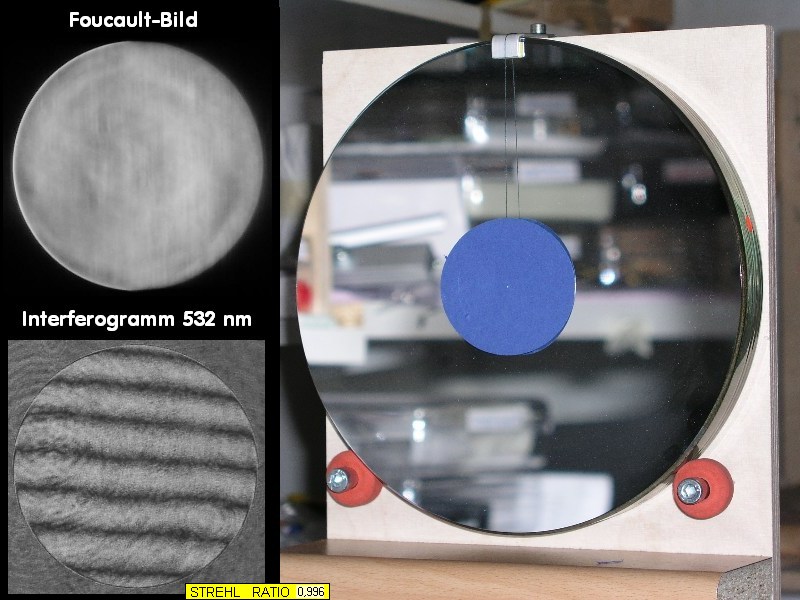
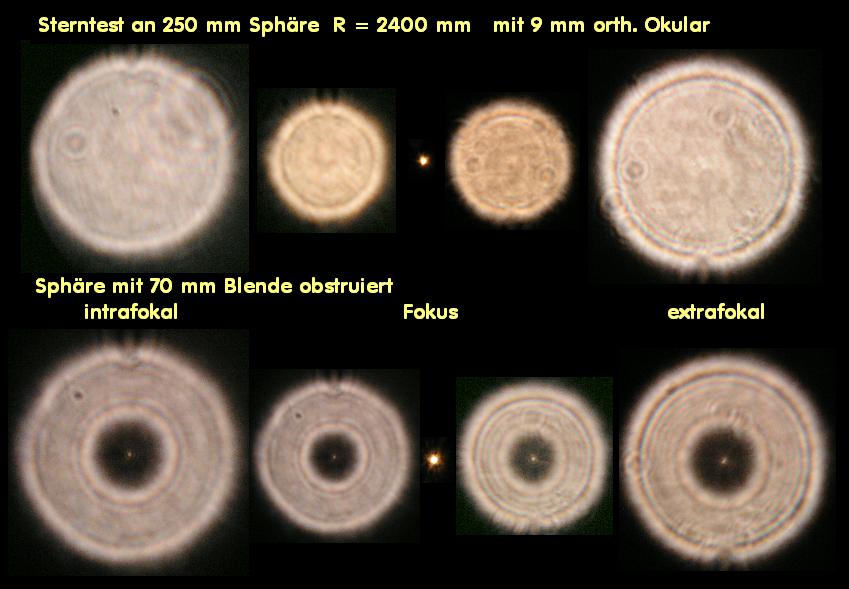
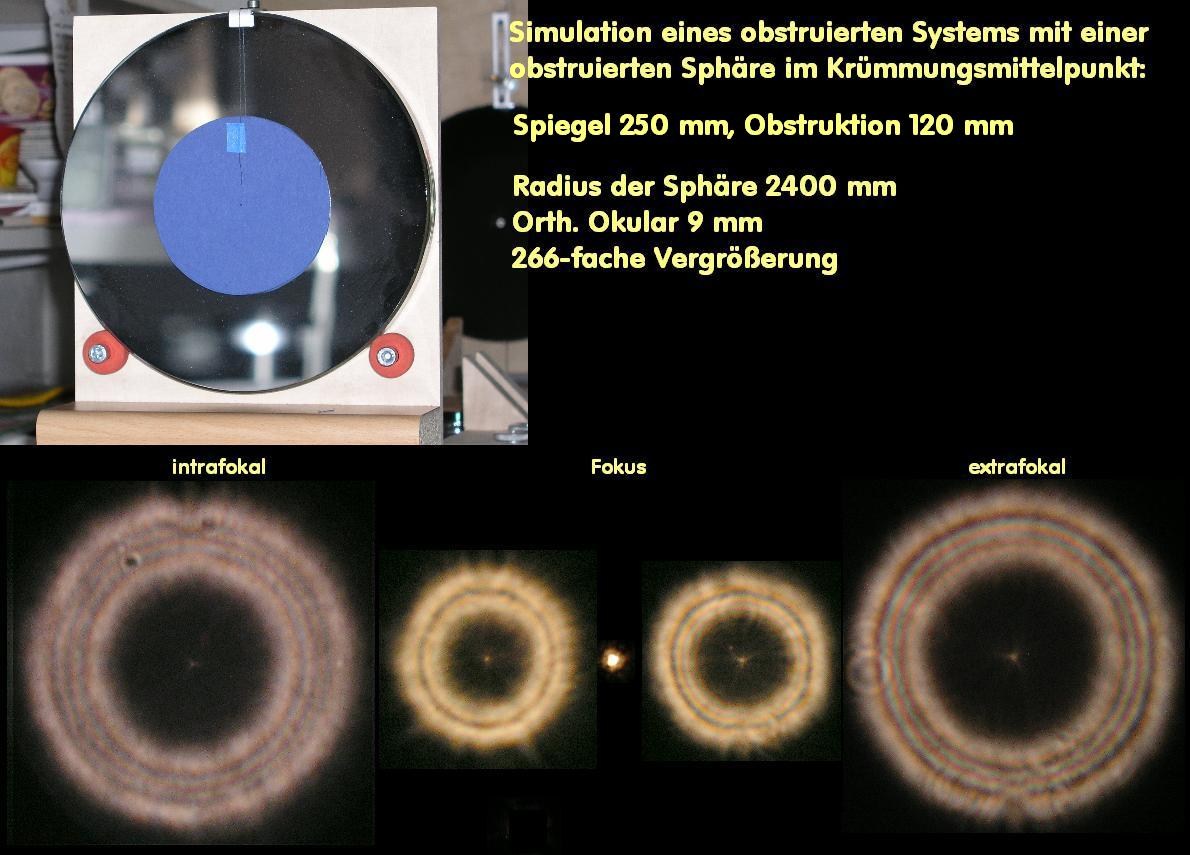
E059 Sterntest - gesammelte fotografische Beispiele aus Berichten
Vorliegender Bericht ist als Zusammenstellung gedacht für die Frage nach dem Sterntest. Die Bilder stammen aus den
jeweiligen Berichten.
12 inch Oldham Newton f/4
16 inch BVC Oldham f/4.4 Newton Rand 32 mm
18 inch BVC Oldham f/4.5 Newton Rand 38 mm rauhe Fläche
20 inch Oldham Der "Trabbi" für Sternfreunde typische Hersteller Merkmale
Bei diesem Hersteller kommen mehrere Merkmale zusammen, die sich auch im Sterntest gut erkennen lassen:
- auffällige Zonen, die sich bereits beim Sterntest abbilden
- abgesunkene Kante bzw. Spiegelrand, dann ist das Sternscheibchen intrafokal ausgefranst, extrafokal mit LichtRand
- Spiegelmitte als Mexikanerhut ausgebildet und in bestimmten Fällen zu stark unterkorrigiert.
- Seltsame Strehl-Berechnung über ZEMAX: Aus einer Foucault-Linien-Messung wird eine ZEMAX-Flächenmessung
(ein Teil dieser Merkmale tauchte bei einem GEOPTIK-Spiegel wieder auf, was auf den gleichen Hersteller schließen läßt)
10 inch Newton vom gleichen Hersteller

Höchst interessanter Vergleich mit einem der besten Spiegelherstellers:
Carl Zambuto Newton 252/1528 Ideal Map bei Atmosfringe
Hier wäre sowohl intra- wie extrafokal der Rand nahezu gleich, die Scheibchen-Fläche außer durch Artefakte über das
Okular verursacht, gleichmäßig ausgeleuchtet. Ein Spiegel, der höchsten Kontrast verspricht.
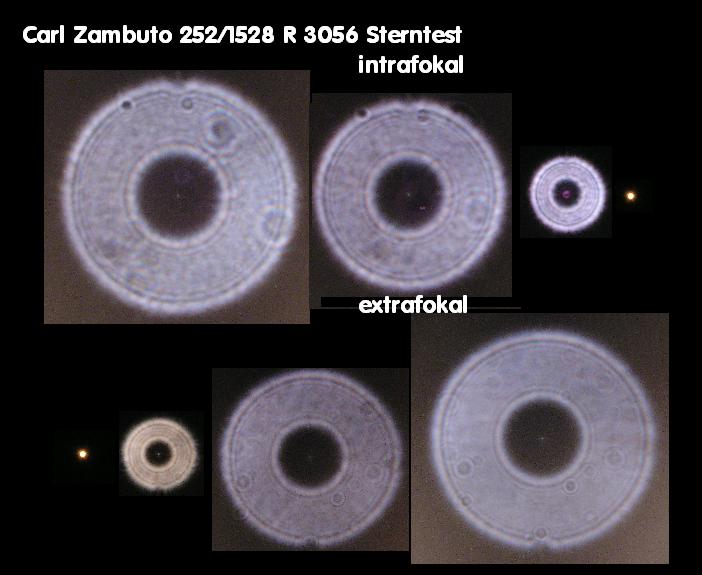
16-inch - ein unbrauchbarer 16-Zöller
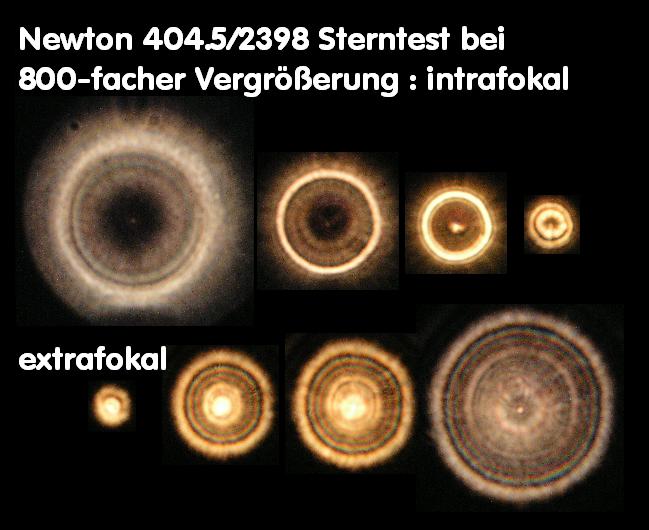
Alluna-20-inch f/4 Newton , Germany
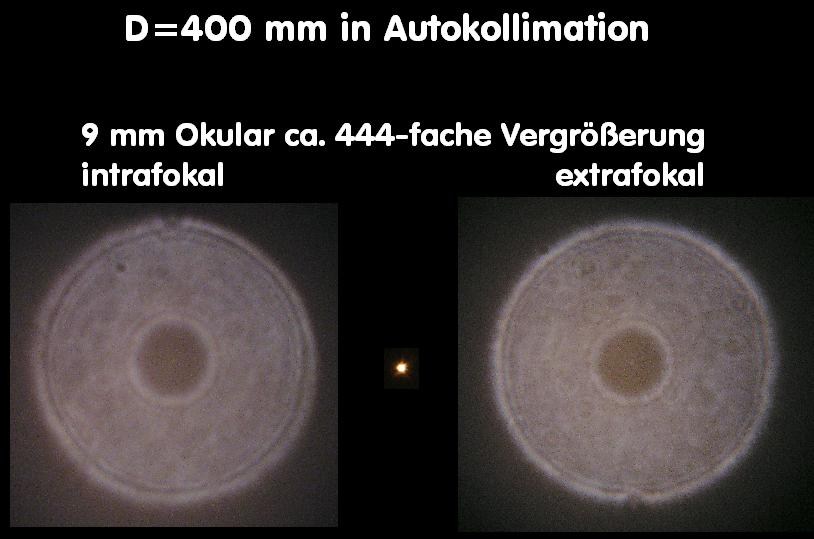
Gladius CF 315/7875 HS_R = 2392 mm
Gladius - Diskussion Teil II mit Paolo Lazzarrotti
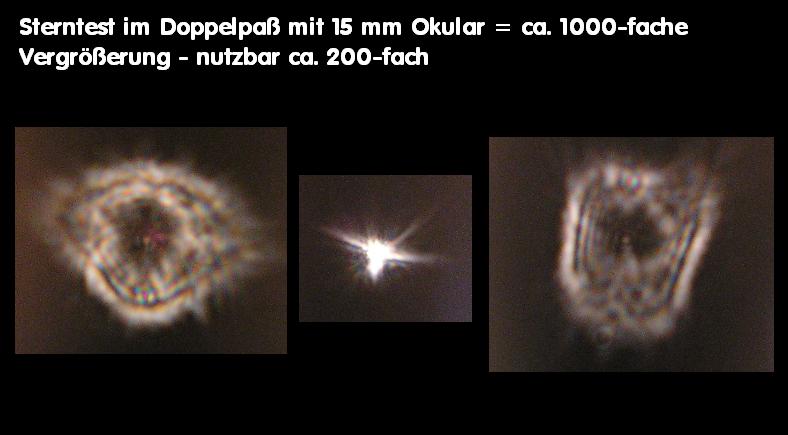
Intes Alter M715 de Luxe ,
Zweifel am Certifikat
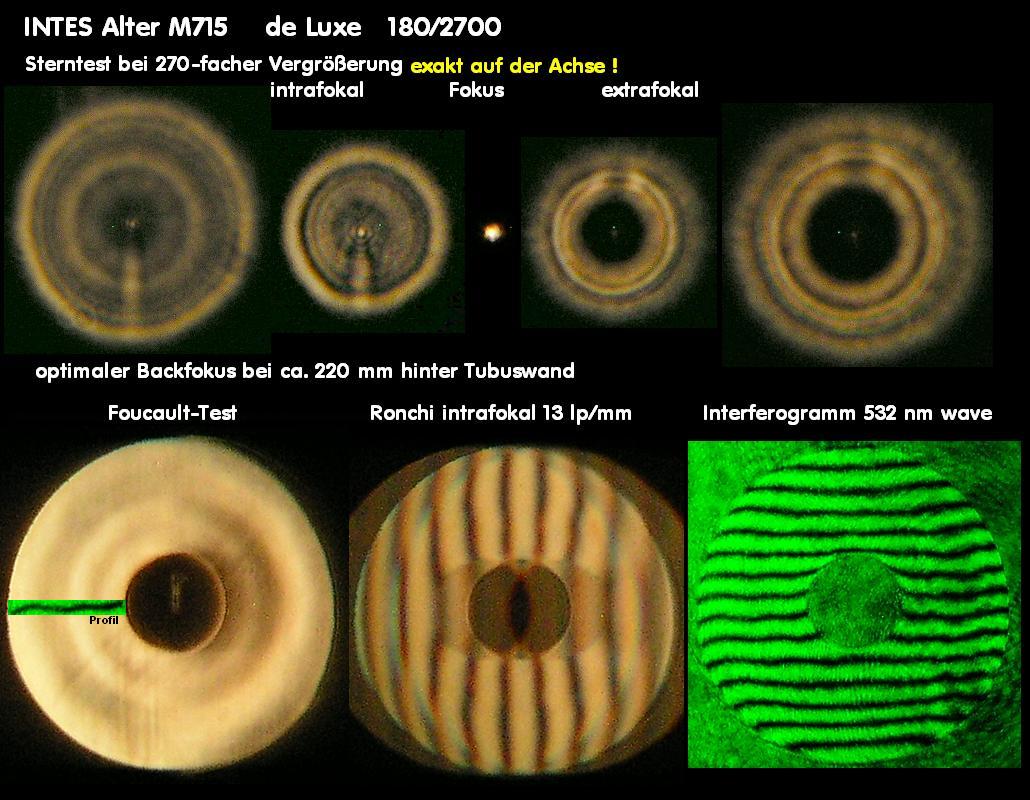
TMB-Nachbau aus China ?

Orion 120 ED Doublet (vermutlich gleicher Hersteller in China wie Equinox)
SkyWatcher Equinox schlägt alles - "den kauf ich mir!"
ED-APO's im Vergleich - SkyWatcher Equinox / EVO Star 120/900
SkyWatcher Equinox 120/900 ED APO Nr. 1
SkyWatcher Equinox ED 120/900 ED APO Nr. 2


Takahashi Super APO TSA 102N 816 erstes Test-Objektiv
Takahashi Super APO TSA 102 / 816 zweites Test-Objektiv
Oldham Spiegel GEOPTIK Newton 406/2025 astigmatisch
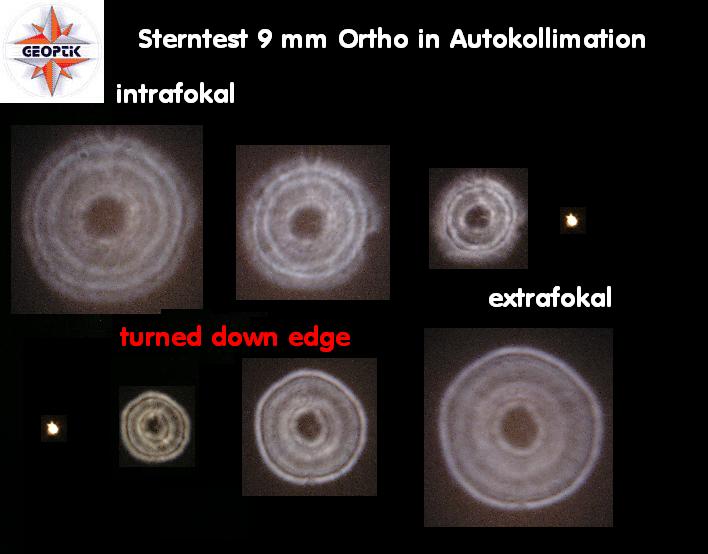
Hubble Optics - leider überkorrigiert
Sandwich 16 inch mit deutlichem Astigmatismus vermutlich Hubble Optics
Hubble Optics 8-inch f/5.7 Newton Messen im Krümmungsmittelpunkt und in Kompensation
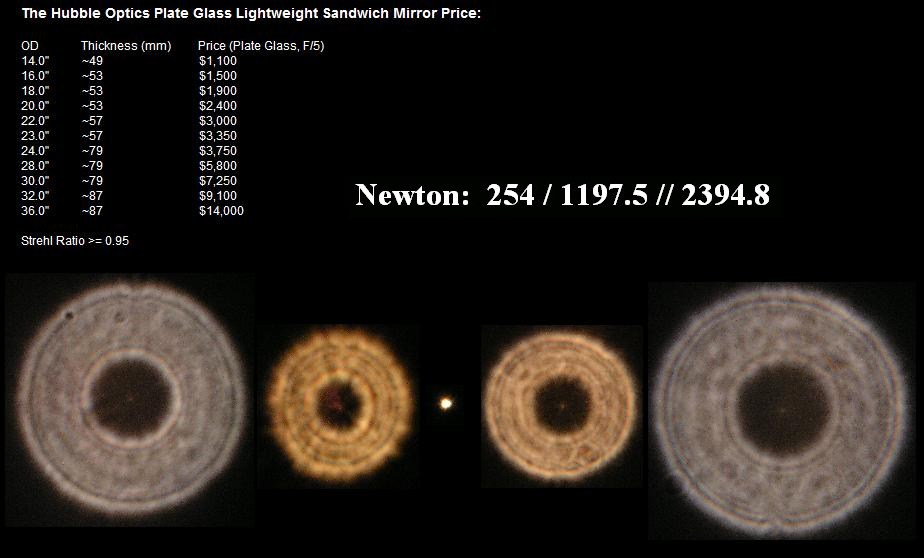
Zwei x LOMO Triplett - 80/600

Meade USA ED-Halb-APO mit Zonenfehlern

Mewlon 180/2160 ein Dall-Kirkham System?
Mewlon 210 sphärischer oder elliptischer Fangspiegel?

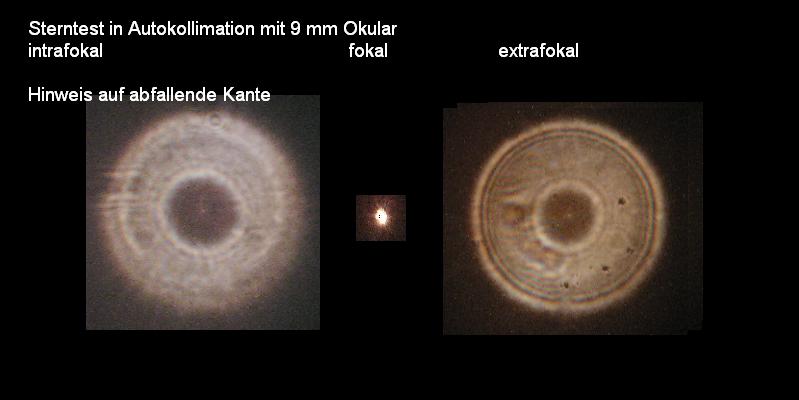
Pentax 75 SDHF, 75/500 Halb-APO
Das zweite Pentax 75 SDHF von Thomas (Petzval-System)
Scopos oder Zenith Star ?
Scopos II 80/560
Scopos III 80/560
great-eye Ein seltsamer APO (Scopos 90/600?)
great-eye Farbreiner Shanghai APO (Scopos 90/600?)

Sky-Watcher ED 80/600 Halb-APO besser mit 50 mm Glasweg
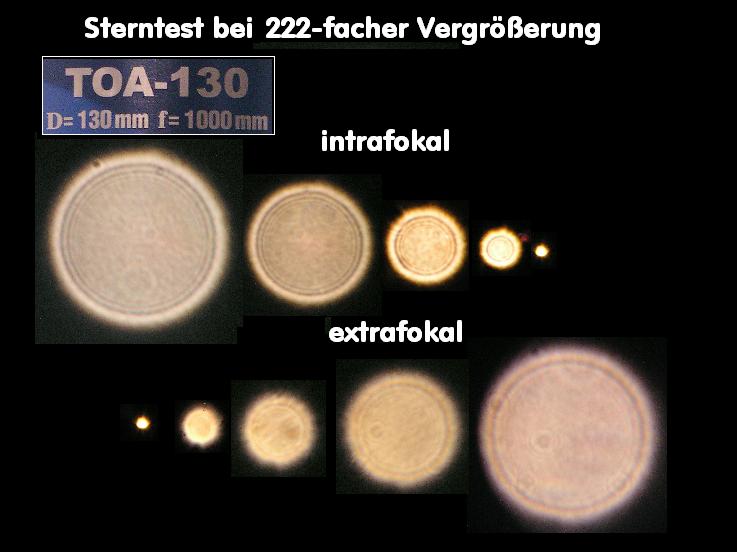
TMB APO Nr. 092 (152/1216)
Quote:
TMB-Sanierung Nr. 105 LZOS Nr. 105/651
TMB APO Nr. 117 - 100/800 mein eigener
TMB 100/800 Nr. 169-22 sehr farbrein
TMB-APO-102/800 Störung der Homogenität
TMB APO Nr. 270 - 115/805
TMB APO Nr. 191 - 152/1216
TMB Super APO 80 / 480 farbiges IGramm
TMB-Nachbau aus China


Zeiss AS 80/1200 Nr. 77571 echter Halb-APO
Quote:
Zeiss AS-Objektive Übersichtstafel
Zeiss AS 80/840 Nr.57865
Zeiss AS 80/840 Nr. 52923
Zeiss AS 80/840 Nr. 55193
Zeiss AS 80/1200 Nr. 77571 echter Halb-APO
Zeiss 100-2000 Halb-APO, Werkstatt/Referenz-Objektiv
Zeiss AS 110/1650 BK7/KzF2 RC-Index 2.1
Zeiss AS 150/2250
Zeiss AS 200/3000
100/1680 Objektiv vermutlich Zeiss AS
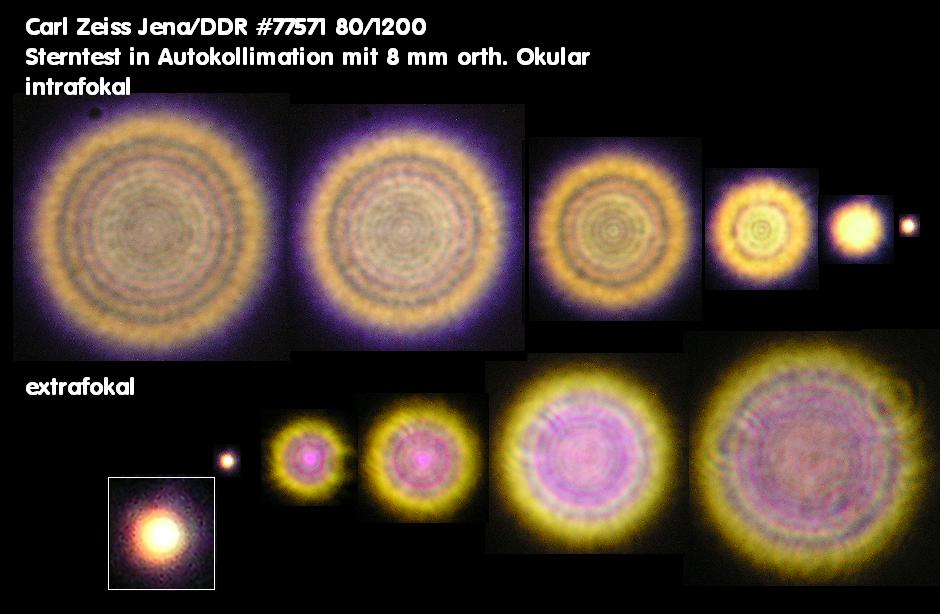
APQ 105/800 zweite Untersuchung
Quote:
Zeiss APQ 130/1000 #97755 - Nur mit Glasweg ein Super-APO
Zeiss APQ 130/1000 # 97161 CaF2-Immersions-Optik: Nur mit Glasweg sehr farbrein
Zeiss APQ 130/1000 #95988 - ohne Glasweg ein guter APO
Carl Zeiss APQ 100/640 Fluorith APO # 97039 mit Glasweg verwenden
Zeiss APQ # 97003 100/640 mit Glasweg verwenden
APQ 105/800 Spannend wie ein Krimi - extrem farbrein

Borg ED 100/640 mit Schlieren.
Borg ED (Halb-Apochromat) 101/650
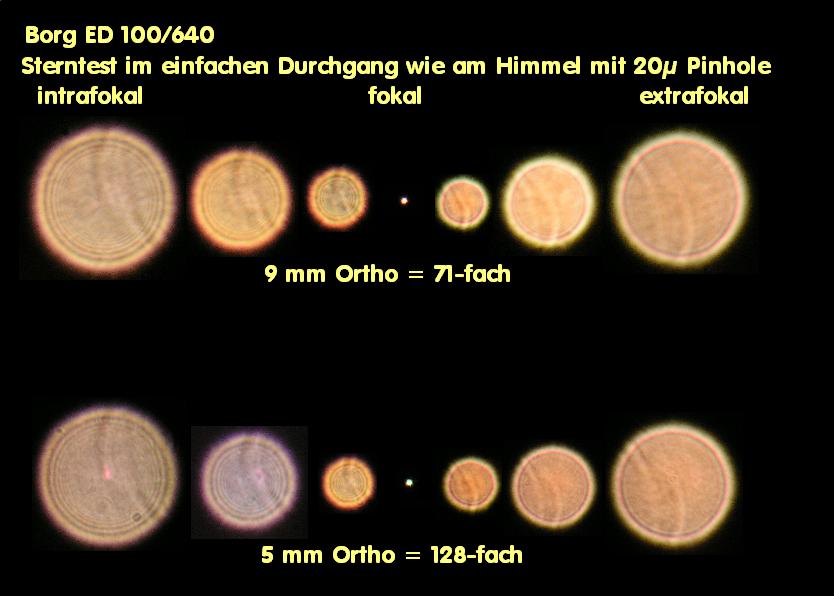
Celestron C 9.25
Quote:
Sehr gutes C 9.25 im Test
Celestron C11 in hoher Qualität
C11 - Reparatur der Fangspiegeleinheit
C11 - nahezu perfekt auf Grün optimiert
Celestron C11 - Einfluß von Back Focal Lenght
Celestron C 9.25 "ein göttliches Gerät"

Zwei China-Maksutovs
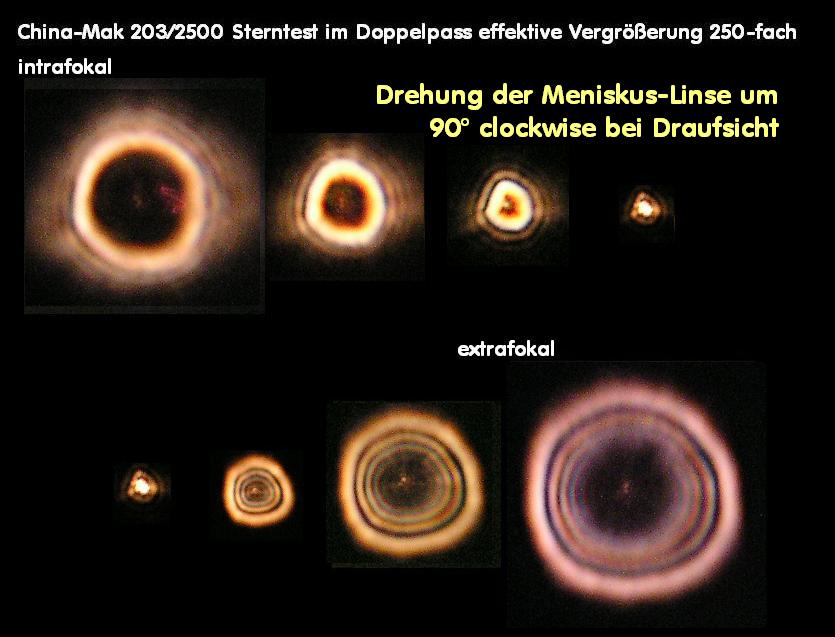
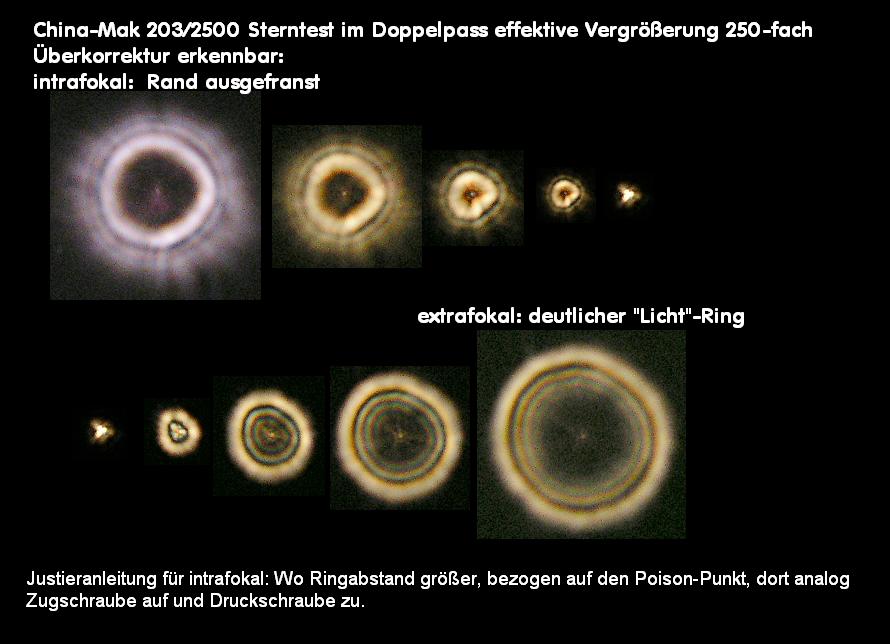
William FluoroStar FLT 132 Vergleich mit Equinox Nr. 1
Ein deutlich überkorrigiertes System, was bereits beim Hersteller ausgemustert werden sollte. Bei einem Refraktor entsteht für
jede Farbe eine ganz eigene Situation bezüglich des Sternscheibchens. Rot wäre gewöhnlich unterkorrigert und Blau überkorrigiert,
wenn das Objektiv die richtigen Linsenabstände hat. Bei einem neuwertigen Objektiv ist dafür aber der Hersteller zuständig, da
dieser Refraktor für ca. 4000.- Euro / 2009 verkauft wird.
Three William FLT 132 strongly overcorrected Nr. 2 und Nr. 3
William Fluoro Star FLT 110 / 770 überkorrigiert

Zwei GSO-Spiegel (16-inch) im Vergleich
Bei diesem Hersteller wird radial retouchiert - leider ! Entsprechend strukturiert zeigt sich die Fläche bereits im Sterntest
und erzeugt mehr Streulicht. Der Kontrast vermindert sich. Allerdings sind es Spiegel für den "kleinen Geldbeutel", und da
nimmt man manches in Kauf, was nicht überall Beifall findet.
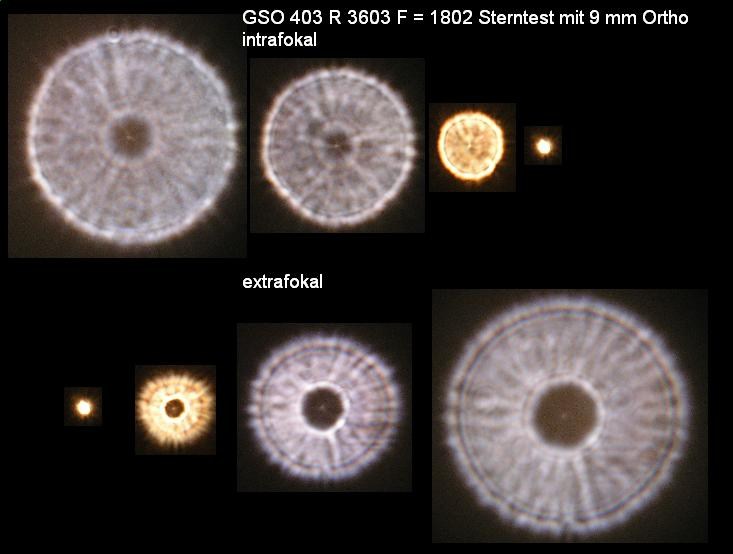
Dieser Test schaut im Krümmungsmittelpunkt einer Sphäre aus, wie ein guter Parabolspiegel am Himmel. Die Sternscheibchen
sollten intra- wie extrafokal gleichbleibend hell erscheinen, der Rand sollte ähnlich bis gleich aussehen. Im Fokus hätte man
eine nadelpunktfömige Abbildung.
Obstruiert man den Kugelspiegel durch eine Scheibe in der Mitte, wie das nächste Bild zeigt, dann bildet sich auch in der Mitte
der bekannte BeugungsRing, wie er bei allen obstruierten Systemen mehr oder weniger deutlich zu Vorschein kommt.

Je größer die Obstruktion, umso stärker ausgeprägt ist der innere Beugungs-Ring, der einen Blick auf die Fläche dazwischen
verwehrt. Solange der nadelfeine PoissonPunkt in der Mitte das RotationsZentrum ist, hätte man es mit einer exakt zentrierten
Optik zu tun. Auch wäre in diesem Fall das System frei von Astigmatismus.

E057 Vertikaler Sterntest bei 20 inch Spiegel - Astigmatismus
Astigmatisch oder nicht?
http://de.wikipedia.org/wiki/Astigmatismus_(Optik)
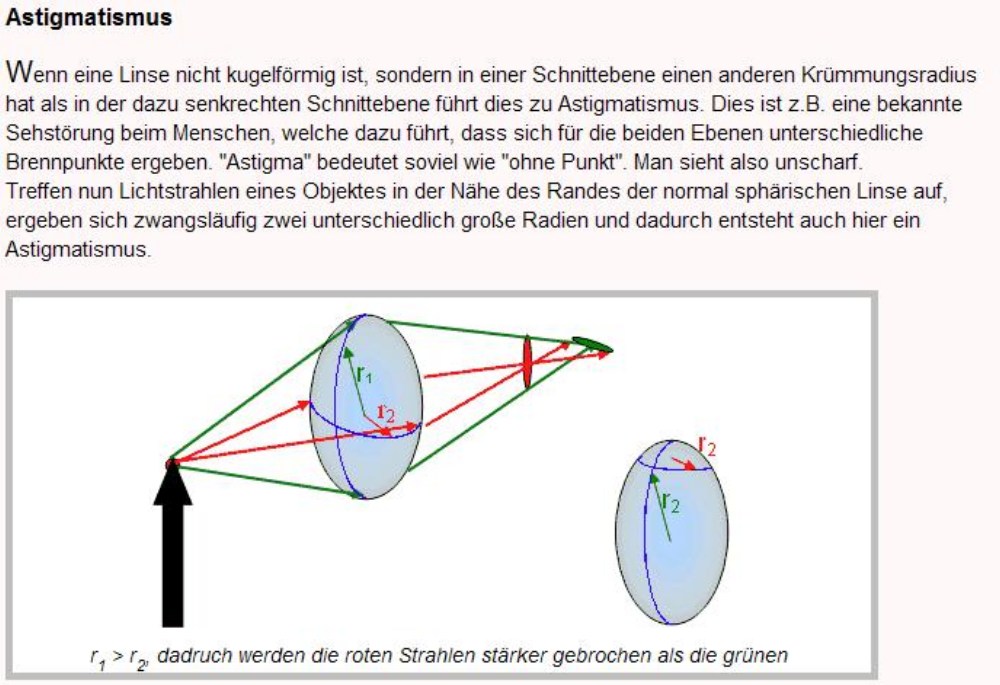
http://rohr.aiax.de/AKA03.jpg, http://rohr.aiax.de/@zern004.jpg, http://rohr.aiax.de/@zern005.jpg
http://rohr.aiax.de/@asti03.jpg, http://rohr.aiax.de/@ATest03.jpg
kleiner Test auf astigmatische Augen
Der Astigmatismus als opt. Zweischalen-Fehler kann den Strehlwert ganz schnell minimieren. Bei Linsen-
Objektiven kann dieser Fehler durch die Fassung aber auch durch die Lage des Objektivs verursacht sein.
Seltener steckt er direkt im opt. System selbst. Bei SC-Systemen vermute ich ihn in der Schmidtplatte, wenn
sie beim Schleif-Prozeß nicht exakt aufgespannt worden ist. Bei kleineren Spiegeln ist er "eingebaut", bei
größeren Spiegeln oft ein Problem der Lagerung und vor allem auch ein Problem, aus welchem Material der
Spiegelträger selbst ist. Oft werden aus Plattenglas runde Scheiben ausgeschnitten, und für diesen Fall spielt
dann auch die Fließrichtung des Glases eine Rolle - entsprechend unterschiedlich biegt sich dann der Spiegel
bei senkrechter Lagerung in einer Schlinge bzw. ein einer 120° Wippen-Lagerung durch.
In diesem speziellen Fall geht es um die Frage, wieviel spiegeleigener Astigmatismus verbleiben denn dann
wirklich am Stern selbst, und nur dann stimmt die Beurteilung des Spiegels. Und selbst dann macht es noch
einen Unterschied, ob man den Spiegel in Zenit-Nähe oder am Polar-Stern prüft.
Auch der Fangspiegel sollte keine weiteren Fehler einführen, also perfekt sein. Der Offset-Punkt sollte eben-
falls stimmen, damit nicht über Vignettierungs-Effekte ein falsches Ergebnis vorgetäuscht wird. Bei f/4
Newton-Systemen spielt bei mittleren Okularbrennweiten noch die exakte Stern-Position auf der Achse (in der
Feldmitte des Okulars) eine Rolle, weil man sonst Koma-Bilder zu sehen bekommt und das Ergebnis erneut
verfälschen. Es bleibt also nichts anderes übrig, am Stern in Zenit-Nähe mit einem ganz kurzbrennweitigen
Okular einen Newton-Spiegel an nicht zu hellen Sternen zu prüfen, ob Astigmatismus vorhanden ist oder nicht.
"Vakuumkamera" von LZOS Lytkarino

Das ist ein 72 m hoher Turm, in dem die Spiegel der russischen Spionagesatelliten horizontal liegend im Strahlengang vertikal gemessen werden.
Es begann damit, daß dieser Spiegel in gleicher Weise (wie beim Hersteller auf dessen Webseite zu studieren)
im 180° Band im Gleichgewicht frei schwingend hängt. In Position Null beim Sterntest im Krümmungsmittel-
punkt von R = 4047 mm extrafokal mit einem 2 mm Nagler Zoom ein sehr gutes Bild, um 90° clockwise ge-
dreht eine elliptische Verformung zeigte. Bereits die Position Null kann eigentlich so nicht stimmen, weil der
500 mm Spiegel eigentlich in sich zusammen fallen muß und dies bei strenger Prüfung auch zeigt. (Der
Spiegelrand = 50 mm breit, das Gurtband hingegen nur 35 mm, damit man nicht in der Nähe der Spiegelkante,
diese wiederum verformt.)

Während in Position Null (roter Pfeil nach oben) bei ca. 1000-facher Vergrößerung das Sternbild mit Luftunruhe recht
ordentlich aussieht, dreht sich bei Pos. + 90° (roter Pfeil nach rechts) offenbar ein vorhandener Astigmatismus mit in
der Form:
Pos. Null = Astig(Spiegel) - Astig(Lagerung)
Pos. +90° = Astig(Spiegel) + Astig(Lagerung)

Wolf-Peter Hartmann erzählte auf dem Bayerischen Teleskop Meeting die mir eigentlich bekannte Tatsache, daß groß-
dimensionierte Newton-Spiegel senkrecht geprüft werden in einem Prüfturm. Im vorliegenden Fall zeigte ein 20 Zoll f/4
Newton-Spiegel je nach Lagerung die unterschiedlichsten Formen von Astigmatismus, also auch drei-eckigen, sodaß
selbst die Philosophie, daß man über eine 90° Drehung des Spiegels selbst den spiegel-eigenen Astigmatismus ermitteln
könne, höchst fragwürdig wurde. Diesen sogenannten Lagerungs-Astigmatismus kann man dann beruhigt herausrechnen
und abziehen, wenn der Sachverhalt eindeutig ist. Aber das kann ein langer Weg sein, und auch die noch so genaue
Band-Lagerung im Gleichgewicht, wie man sie auf den Webseiten einiger Hersteller findet hilft nichtbei der Lösung des
Problems. Um einen größeren Newton-Spiegel mit einfacher Genauigkeit prüfen zu können, muß man tatsächlich über
ein Kompensations-System in einen Prüfturm, den ein normaler Amateur-Prüfer nicht hat - aber er hat ein comfortables
Treppenhaus, und dort läßt sich die Meßstrecke von 4047 mm problemlos in der Vertikalen realisieren. Am Ende muß
aber auch ein Sterntest - möglichst mit Dokumentation - endgültige Klarheit bringen.
Nachts um 02:00 Uhr, wenn die Gattin schläft, wird ihr heiliges, ziemlich teures Treppenhaus in einen Prüfturm umfunk-
tioniert. Nur das Vakuum würde man als Prüfer nicht überleben, also hat man es auch hier mit der üblichen Luftbewe-
gung zu tun. Die gedrechselten Verbindungs-Stäbe dienen zweckentfremdet als Halter für den Prüftisch, natürlich so,
daß man keine Blessuren hinterläßt, wenn einem der Familien-Frieden etwas wert ist.

Mit einem Laserpointer von oben läßt sich problemlos der einen Stock tiefer gelagerte Hauptspiegel in die richtige Lage
bringen. Danach schaut man sich einen künstlichen Stern, 20µ Durchmesser mit einem 2 mm Okular, Nagler Zoom, an.

Im ersten Durchgang lag der Spiegel auf einer Blasenfolie, 2 cm Blasengröße, wie sie zur Isolation es eigenen Gewächs-
hauses hervorragende Dienste leistet. Aber auch hier ist noch nicht restlos garantiert, ob der Spiegel absolut verfor-
mungsfrei gelagert ist.

Bei ganz kritischer Beobachtung könnte man noch einen Astigmatismus in Richtung 07:00 - 13:00 Uhr ausmachen, was
aber in der Luftbewegung unterzugehen scheint.

Deswegen ein zweiter Versuch über die Lagerung auf den Luftkammern einer Luftmatraze. Hier sollte der Spiegel
gleichmäßig von unten gleichmäßg gelagert sein. Diese Lagerung wurde zweimal wiederholt mit immer gleichen
Ergebnissen.

Aber auch hier erkennt man noch eine Veränderung des Sternscheibchens, wobei die Vergrößerung mit dem 2 mm Okular
bei ca. 1000-fach liegt und damit hinreichend genau sein sollte. Ein letzter Test wird hoffentlich am Himmel selbst Klar-
heit bringen, wenn der Spiegel auf einer 18-Punkt Lagerung auf der Achse zeigen soll, ob er frei von Astigmatismus ist
oder nicht. Und dann läßt sich ein Astigmatismus eindeutig als Lagerungs-Astigmatismus abziehen, und einigen fiele
ein großer Stein vom Herzen.

E056 mein eigener Lyot-Testaufbau mit Filmnegativ Filterlinien TP 2415
Mein eigener Lyot-Test-Aufbau:
(Siehe dazu den MediaWiki-Eintrag u. Testaufbau von Herbert Highstone.)
Der GesamtTestaufbau funktioniert so ähnlich wie der Foucault-Test. Statt der Messerschneide/Klinge steht an derselben Stelle nun
der Filterstreifen/Linie. Das ist auch der Grund, warum dieser Aufbau auch als Foucault-Test verwendet werden kann mit besserer
Auflösung. Benutzt man die Filterlinie auf dem Filmnegativ am Rand als Messerschneide, dann entsteht ein Foucault-Bild, wie unten
zu sehen. Steht hingegen der Lichtspalt mittig vor dem Filterstreifen, zeigt der Testaufbau als Lyot-Test die Feinstruktur der Fläche,
Bild unten rechts.

So ähnlich müßte also auch bei anderen der Lyot-Testaufbau aussehen. Wichtigstes Hilfsmittel ist links a) der Lichtspalt möglichst
dünn zwischen 10µ und 30µ. Zu breit läßt die Bilder flau werden. Dahinter b) ein Diarahmen mit einem TP 2415 Negativ-Film mit
mehreren halbdurchlässigen Filterlinien etwa 2.xxx density und unscharfe Kanten bei 0.1 mm Breite. Hier variieren die einzelnen
Tester. Auch Filterlinien aus Ruß von einer Kerzenflamme funktionieren. Genauer zeigt es die Detailansicht Filterlinie und in ihrer
Vergrößerung rechts. (Verstellbarer Lichtspalt, groß, Filmnegativ TP2415 mit Filterlinien )

Mich würde nun interessieren, ob es von diesem Testaufbau auch ganz andere Varianten gibt.
Vom User Horia gibt es auf AstroTreff eine brauchbare Zusammenfassung:
Horia 10.01.2014 : 22:18:29 Uhr http://www.astrotreff.de/topic.asp?TOPIC_ID=159676&whichpage=28
Quote:
Hallo allerseits, bezüglich der Messprozedur von David:
Er sucht sich mehrere Maximalwerte auf der Oberfläche und, mit Hilfe des Graukeils, rechnet den jeweiligen z-Wert.
Diese Werte werden dann gemittelt und ergeben den Peak-Wert. Das gleiche wird dann für mehrere Minimalwerte auf
der Oberfläche, um den Valey-Wert zu ermitteln. Die Differenz ergibt dann den Peak-To-Valey Wert als Mittelwert.
Ich finde die Methode optimal, für eine rein manuelle Auswertung.
Aus den PtV wird dann nach Gefühl ein rms-Wert deklariert. Das ist nicht mehr ganz richtig, das Ergebnis dürfte jedoch
akzeptabel sein. Ich kann eigentlich die Grundidee dieser Methode gut verstehen: David ist Spiegelhersteller und für ihm
ist wichtig sagen zu können "die Politur ist besser als so und so viel" und nicht den genauen Wert.
Es wäre eigentlich eine relativ einfache Programmieraufgabe, die Grauwerte aller Pixel mit dem Graukeil zu vergleichen
und so - für alle Pixel der Oberfläche - die Amplitude zu berechnen. Daraus lässt sich dann der RMS-Wert berechnen,
als Wurzel aus ((Mittelwert der Quadraten) - (Quadrat des Mittelwertes)).
Es gibt selbstverständlich einige Fehlerquellen bei der Ermittlung der PtV-Werte, so dass eine Vergleich-Messung mit
eine Industrielle Methode zu Kalibrierung sehr nützlich wäre.
GrauKeil Bild mit Dichte: http://www.astrosurf.com/ubb/Forum2/HTML/039889-27.html
Streulicht aus unterschiedlichen Quellen
E055 Lyot Test with a thin soot filter line
Lyot Test with a thin soot filter line - Rauhheits-Test für Optiken
more links about Lyot test:
http://www.google.com/search?q=%22Lyot+Tes...8&start=10&sa=N
http://www.starastronomy.org/Library/Spect...ram-06-2002.pdf
http://www.astrosurf.com/tests/contrast/contrast.htm
http://www.vision.fraunhofer.de/de/2/projekte/148.html
Herbert Highstone gave me the idea, to make a small line filter from soot. This one you
need it for the Lyot or Phase Contrast test. There are different ways to produce that
line filters: with a negative film TP 2415, with an overcoated line with the density d=2.16,
and at last with soot and a mask, to produce a small line on a glas plate.
The following shows the steps.

This is the soot line filter on a glas plate

This is the mask. You put the glas plate on it and fix it with a holder, because it will
become hot with the candle light

All three parts. In the middle the mask from the backside with soot and the candle
for getting the soot. In this way you can produce filters on a glas plate for watching
the sun, but we just need a small filter line.

This shows the light split and the filter line.
An exposure with this soot filter line

This is one with the film negative filter line. Now with some more experiences lets
find out how much is the density of that filter and how thin it must be for optimum.
Best regards with your own experiences! Would you kepp me informed?
Wolfgang Rohr
#######################################################################################
Nein, lieber Dietmar, es ist keine abgefeimte, böse Absicht. Es steckt etwas ganz
anderes dahinter. Da gibt es die http://groups.yahoo.com/group/interferometry/
also ein Sammelplatz von Leuten, mehrheitlich aus USA, die sich sowohl für den
Bath-Interferometer wie auch den Lyot- oder Phasenkontrast-Test interessieren.
Besonders auch ein Herbert Highstone. Und einer von denen hat doch unlängst
meinen englischen Beitrag zum Bath-Interferometer auf dem Stoffie-Board ent-
deckt. Das war das erste Motiv, diese Sternfreunde anzusprechen, weil man einen
solchen Bericht entweder auf seine Webseiten nimmt, oder in eines der Foren.
Das hätte vielleicht den von mir erhofften Effekt, daß wir auch User aus dem
engl. Sprachraum bekommen, die oftmals sehr viel undeutscher, also unbefange-
ner mit der Sache umgehen, und weniger Wert auf die Begleitumstände legen.
Überdies gehe ich davon aus, daß im Internet-Zeitalter das Englische zur zweiten
Muttersprache geworden ist, bzw. Du ja auch zweisprachig lebst.
Zusätzlich schreibe ich ja keine Aufklärungs-Schrift für optisch Unbedarfte, sondern
einen Beitrag, der in anderer Weise auf AstroTreff diskutiert wird. Dort geht es um
die quantitative Erfassung von Streulicht, was ich für sehr schwierig halte. In
meinem Beitrag geht es um die Herstellung eines dünnen Linienfilters mittels
Kerzen-Ruß, damit man die Rauhigkeit von Flächen sichtbar machen kann, was
eine Voraussetzung für die Streulicht-Diskussion ist. Neben der üblichen Topo-
grafie, wie sie der Foucault-Test bereits zeigt, erhält man über den Lyot-Test
eine zusätzliche streulicht-erzeugende Feinstruktur. Das größte Problem dabei
ist, das Bild in irgendeiner Weise quantifizieren zu können, in dem Sinn, wie hoch
in Nanometer diese Rauhheit eigentlich ist.
Praxis-relevant wird dies im Falle eines 490/2020 Spiegels aus SCARBOROUGH,
NORTH YORKSHIRE, UK, daß sich die Kontrast-Einbußen an den Planeten offenbar
mit meinen Rauhheits-Messungen decken.
Mein 320/1600 Spiegel schaut am gleichen Test etwa so aus.

Das Argument, daß glatte Spiegel am Himmel weitaus mehr Kontrast bringen hat
schon Texereau in seinen Buch beschrieben und Malacara ebenso. In einem
anderen Beispiel war es ein VMC dessen dicke Speichen und kräftige Unterkorrektur eine andere Form von Streulicht verursachte, was mehr mit der
spherischen Aberration zu tun hat.
Streulicht-Messung ist also nicht nur ein neues verkaufsförderndes Argument von
Händlern, wie andernorts behauptet wird, sondern über die Literatur schon sehr alt,
auch wenn es erneut wieder stärker ins Blickfeld rückt. Unter anderem bei den
Sternfreunden aus USA.
E054 Jean Texereau Micromammelonnage OrginalSchrift MärzApril 1950

.

.
.

.

.

.
.

.

.

.

.
.

.

.

.

.

.

.

.

.
.
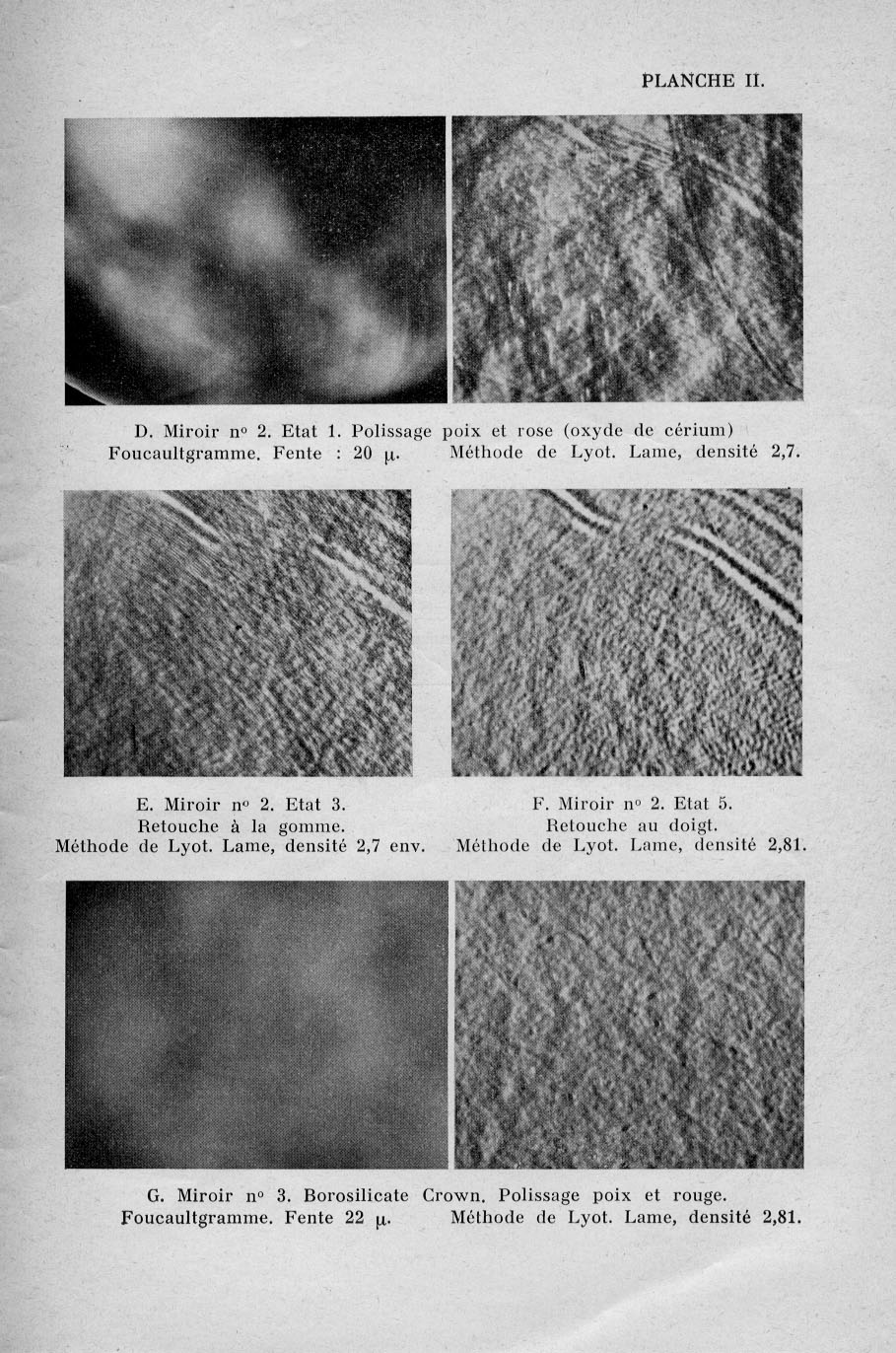
.
.
E049 Spiegel-Rauhheit im Vergleich - Übersicht von Newton-Spiegeln
siehe auch E050 * Rauheit, Foucault, Lyot, Streulicht - Diskussion mit Dr. Weischer
Einleitung:
Eine Definitions-Einheit für Oberflächen-Rauhheit im Quadrat-Zentimeterbereich, gibt es nicht. Das wäre nämlich der Bereich,
innerhalb dessen man die Rauhheit bei Newton-Spiegel darstellen kann über den Lyot-Test. An den folgenden Beispielen kann
man also nur die Ergebnissse der Polier-Technik studieren und darüber vergleichen, ob ein Spiegel glatter oder rauher ist. Viele
der Massen-Spiegel aus China sind rauh, aber äußerst preiswert. Viele Beobachter merken am Himmel den Unterschied gar nicht.
Quote:
Bei der Rauheits-Diskussion muß man dringend unterscheiden zwischen der großdminensionierten Topografie
der Wellenfront auf der einen Seite. Dazu zählen Zonen, abgesunkene Kante, Über oder Unterkorrektur.
Auf der anderen Seite erzeugt die Flächenfeinstruktur, wie sie im Nachfolgenden gemeint ist, erhebliches
Streulicht, was ganz besonders die visuelle Nutzung einer Spiegeloptik beeinträchtigt. Für die Fotografie spielt
diese Art Rauhheit eine eher untergeordnete Rolle. Da werden selbst Aufnahmen mit rauhen Spiegeln noch
be-eindruckend. Für die visuelle Nutzung ist die "Glätte" einer Optik von großer Bedeutung. Ein gutes Test-
objekt für die hier gemeinte Rauhheit sind die Komponenten E und F im Orion Trapez, die nur bei glatten
Spiegeln klar definiert werden. Bei rauhen Spiegeln verschwinden diese feinen Sterne.
Diese Rauheit spielt immer dann eine Rolle, wenn Streulicht den Kontrast vermindert und ein lichtschwaches
Objekt neben einem hellen Stern im Streulicht "untergeht" . Auch die Sonnenbeobachter bevorzugen besonders
glatte Optiken.
http://www.intercon-spacetec.de/rat/rat-teleskope/welches-teleskop/optischequalitaet/
Quote:
RMS
Zunächst muß sich die Industrie den Vorwurf gefallen lassen, daß RMS auch der geschönten Zahlendarstellung dient. RMS, Root Mean Square, ist eine gemittelte Durchschnittsabweichung, der RMS-Wert ist mindestens 3,3 mal schöner als der PV-Wert. Besonders unfair ist, wenn RMS-Werte beworben werden, ohne ausdrücklich als solche gekennzeichnet zu sein.
Wenn man RMS-Werte als solche erkennt und damit umgehen kann, lassen sie genaue Rückschlüsse auf die Abbildungsleistung eines Teleskopes zu. Bei modernen Testprotokollen, d.h. Interferogramm mit Computerauswertung, ist der RMS-Wert die einzige sinnvolle Auswertung. Wie RMS, PV und Kontrastleistung zusammenhängen, zeigt folgende Abbildung:
Spiegel A und Spiegel B weisen die gleiche PV-Oberflächengenauigkeit von 1/4 PV auf. Spiegel A ist "rauh", d.h. die Spiegeloberfläche schwankt ständig zwischen Maximum und Minimum. Wahrscheinlich enthält dieser Spiegel eine Stelle mit größerem Fehler, die in dieser Messung nicht gefunden wurde. Die RMS-Oberflächengenauigkeit beträgt nur 1/16 RMS, die von diesem Spiegel gelieferte Kontrastschärfe ist unbrauchbar.
Spiegel B hat die gleiche PV-Oberflächengenauigkeit von 1/4 PV. Dieser Oberflächenfehler ist jedoch auf 1/1000 der Gesamtfläche begrenzt, und bei einem scharf gestellten Bild defakto unsichtbar. Mit etwas Glück oder bei entsprechender Anzahl von Messungen wäre diese Stelle auch durch den Messraster gefallen, d.h. dieser Spiegel könnte genausogut eine Genauigkeit von 1/8 PV im Protokoll haben. Bei der RMS-Auswertung fließt die Glätte des Spiegels erheblich ins Messergebnis ein, der Spiegel ist besser 1/30 RMS. Mit kleiner Obstruktion kommt die Kontrastschärfe in brauchbare Bereiche. Diese beiden Extrembeispiele sind von der Praxis gar nicht so weit entfernt. Jeder erfahrene Astronom kennt die Regel, daß die Kontrastleistung eines Spiegels nicht direkt aus dem PV Oberflächenwert abzuleiten ist, sondern eben auch entscheidend die Glätte hinzu kommt. Das extremste mir bis jetzt bekannte Testprotokoll weist für einen 10" f/4,8 eine PV wavefront Bildgenauigkeit von "nur" 1/3,6 aus, also nicht mal 1/4 PV. Wenn man sich nicht auf nur 2 Meßwerte beschränkt sondern die übrigen 50.000 digital ermittelten Meßwerte zu Rate zieht, kommt ein RMS-Wert von 1/28 wavefront heraus. Daneben weist das Protokoll einen Strehl-Wert von 0,95 aus, d.h. die Optik ist gerade mal 5% schlechter als ein theoretisches Ideal. Ohne Zweifel würde ein Interferogramm über 500 Testpunkte einen deutlich besseren PV-Wert ausweisen, und jeder manuelle Test würde die Oberflächengenauigkeit im Bereich von 1/20 PV ansiedeln.
Spiegel-Rauhheit im Vergleich - alles Lyot-Testaufnahmen
Bei einem Thread ähnlichen Titels hat zumindest eine Anregung von Günter ergeben, eine Übersicht zu
erstellen von ganz unterschiedlich rauhen oder auch glatten Spiegeln, je nachdem welchen Begriffen man
zugeneigt ist. Bei jedem dieser Beispiele handelt es sich um ein Unikat. Das ist besonders am LOMO Beispiel
erkennbar. Ein und derselbe Hersteller liefert einmal besonders glatte, manchmal aber auch rauhe Spiegel
ab. Bei anderen Herstellern kann man eine Entwicklung hin zu immer glatteren Spiegeln beobachten. In
dieser Übersicht geht es also nur darum, wie ein besonders glatter Newton-Spiegel aussieht und wann man
bestimmt von einem rauhen Spiegel sprechen muß. Aber auch ein rauher Spiegel kann theoretisch einen
Strehlwert von 0.99 haben, wenn er beispielsweise eine perfekte Parabel hat - meist jedoch nicht.
Man möge unseren Begriff Rauhheit nicht mit der DIN Norm überziehen, weil unser Begriff von der Spiegelschleifer-
Szene geprägt wurde und u.a. als ripple und micro ripple in deren Literatur eingegangen ist.
In Frankreich - ein Land wo der Lyot-Test weit verbreitet ist - gibt es einen mir bekannten Spiegelschleifer, der wohl
die glattesten Spiegel überhaupt herstellen kann, die ich gesehen habe.

Mein eigener Spiegel hat ebenfalls eine extreme Glätte. Den Hersteller wollte mir der Händler begreiflicherweise nicht
nennen. http://www.astro-foren.de/showthread.php?p=31024#post31024

Dieser Hersteller hat in der Regel ziemlich glatte Spiegel, ich habe hier auch nicht ganz so gute Beispiele.
Ein Hersteller, der sich in den letzten Jahren gewaltig gesteigert hat auch was die Glätte betrifft.
http://astro-foren.de/index.php/Thread/4388-Die-Orion-Zwillinge-dem-Barry-gewidmet/

Offenbar ist es auch materialabhängig, wie glatt eine Oberfläche wird.
zählt ebenfalls zu den glatten Spiegeln http://www.astro-foren.de/showthread.php?p=33916#post33916
Wegen des großen Durchmessers habe ich gegen zweio Planspiegel geprüft
auch hier noch ein glatter Flächeneindruck mit feinen Rillen, deren Ursache mir nicht klar sind.
Ein typischer GSO Spiegel mit der typischen Radial-Struktur - könnte bereits ein BK7 Spiegel sein.
feine micro ripples, trotzdem glatter Flächeneindruck
Auch bei LOMO - wer immer letztlich die Spiegel unter diesem Namen hergestellt hat - fallen die Ergebnisse unterschied-
lich aus. Nummer 5 habe ich für mich behalten. Ein erstklassiger kontrastreicher Spiegel bei gutem Seeing.
C048 - Drei hochwertige Dobsons
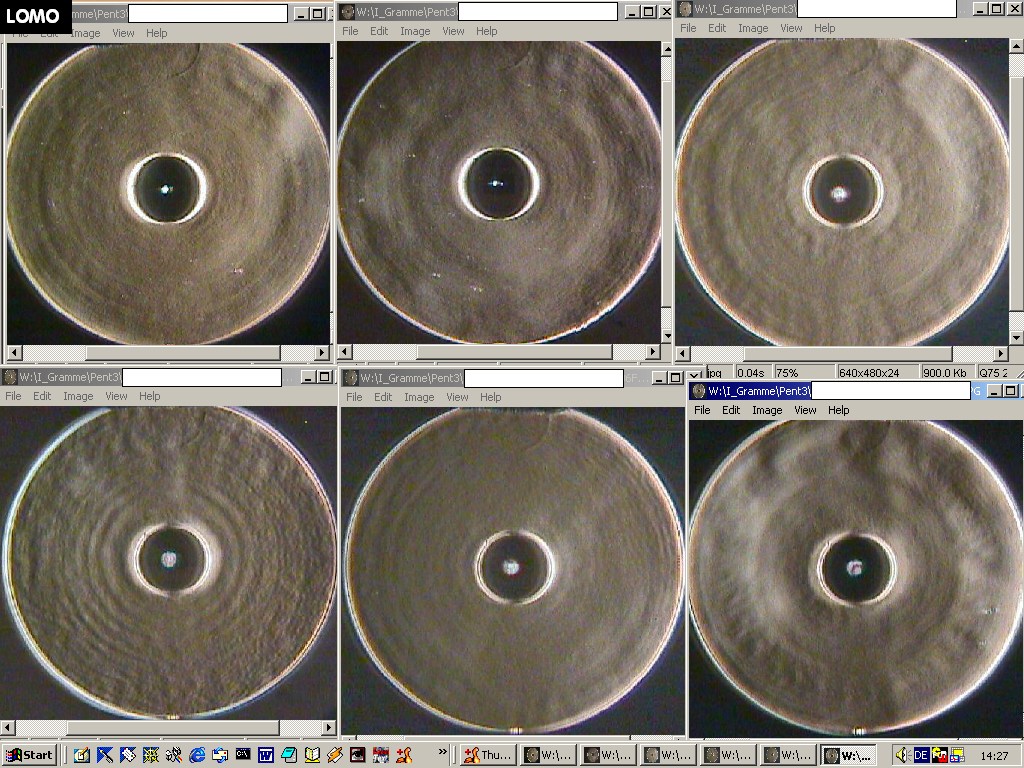
Die "Rauhheit" dieses Spiegels wird man am Himmel vermutlich weniger wahrnehmen. Der Streulicht-Anteil wird etwas
höher sein, als bei einem sehr glatten Spiegel.
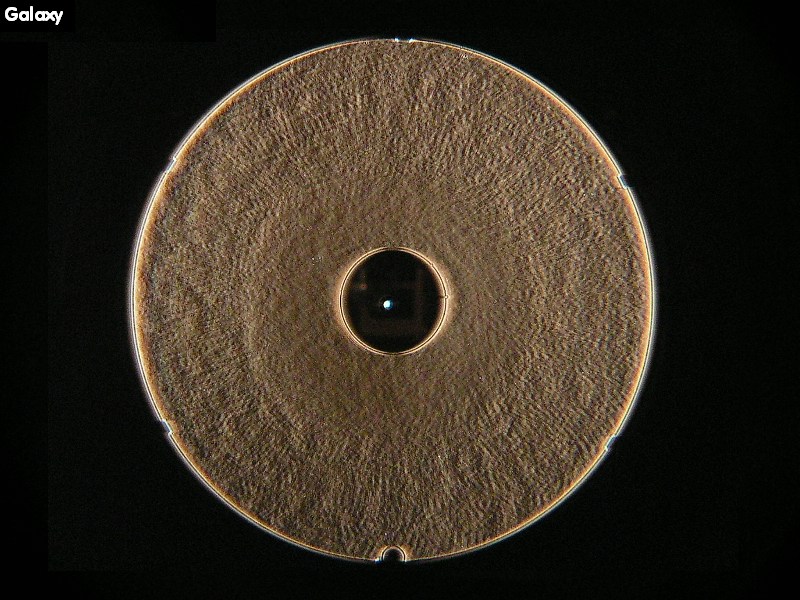
Das dürfte die übliche Qualität an Spiegelglätte sein, wie sie auch bei den folgenden Spiegeln erkennbar ist.

Die Parabel stimmt in der Regel, aber der Lyot-Test zeigt trotzdem eine rauhe Fläche.
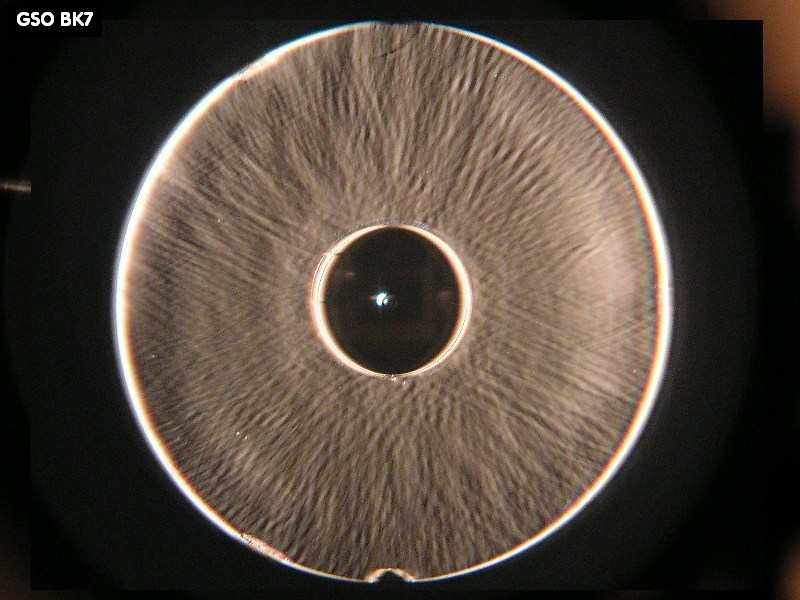
Hier sind es in der Regel unüberlegte Polierstriche und ihre Auswirkungen im Lyotgraph

Auch hier "pflügt" der Spiegelschleifer über die Facetten tiefe Furchen in die Fläche des Randes. Unter einer Halogen-
Lampe zeigt sich die 0.7 Zone noch matt, weshalb dieser Spiegel reklamiert worden war.
http://astro-foren.de/index.php/Thread/6368-Die-%C3%9Cberraschung-kam-zuletzt/
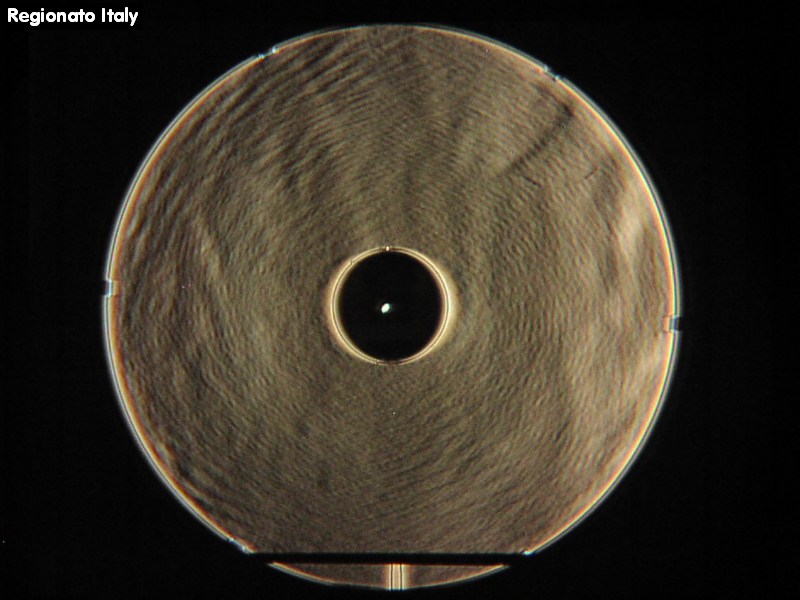
Dieser als Premium Spiegel deklarierte Newton hat, wenn man den spiegeleigenen Astigmatismus zuläßt, einen ziemlich
niedrigen Strehlwert: http://www.astro-foren.de/showthread.php?p=34245#post34245
Hauptprobem hier ist nicht die Rauhheit, sondern die Formabweichung.
Auch dieser Hersteller hat ganz typische Merkmale mit denen man seine Spiegelidentifizieren kann.
http://astro-foren.de/index.php/Thread/8596-Ein-merkw%C3%BCrdiger-Newton/
Ein BVC 18-Zoll Spiegel vor einem 16-Zoll Planspiegel http://www.astro-foren.de/showpost.php?p=34483&postcount=2

Auch diese Form der "Rauhheit" ist vertreten.
Auch dieser Spiegel, für ein Institut geschliffen, machte den Studenten, der glaubte, ein Schnäppchen gekauft zu haben, später tot unglücklich.
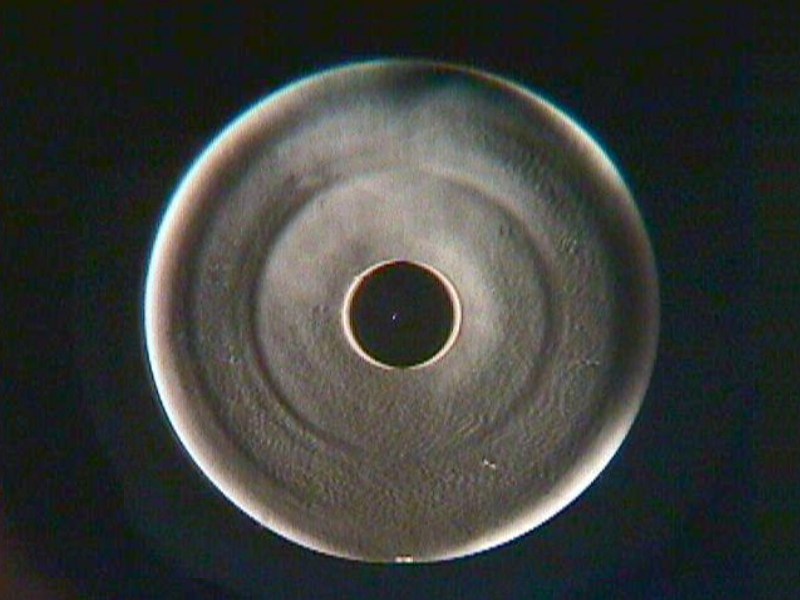
#############################################################################
Weitere Quellen:
http://www.astrosurf.com/tests/articles/contrast/contrast.htm
http://www.astrosurf.com/tests/defauts/defauts.htm#rugosite
http://www.astrosurf.com/tests/test460/test460.htm#haut
http://www.astrosurf.com/tests/defauts/fig2b.htm
Vous pouvez télécharger cette référence à l’adresse suivante : www.astrosurf.com/tests/biblio/contrast.zip
Daniel Malacara "Optical Shop Testing", Third Edition, 2007 by John Wiley Sons Inc, Kap. 8.5.2 Lyot Test S 305-307 ff
Jean Texereau "How to Make a Telescope" Second Edition, 1984 Willman-Bell, Inc, Richmond, Virginia,
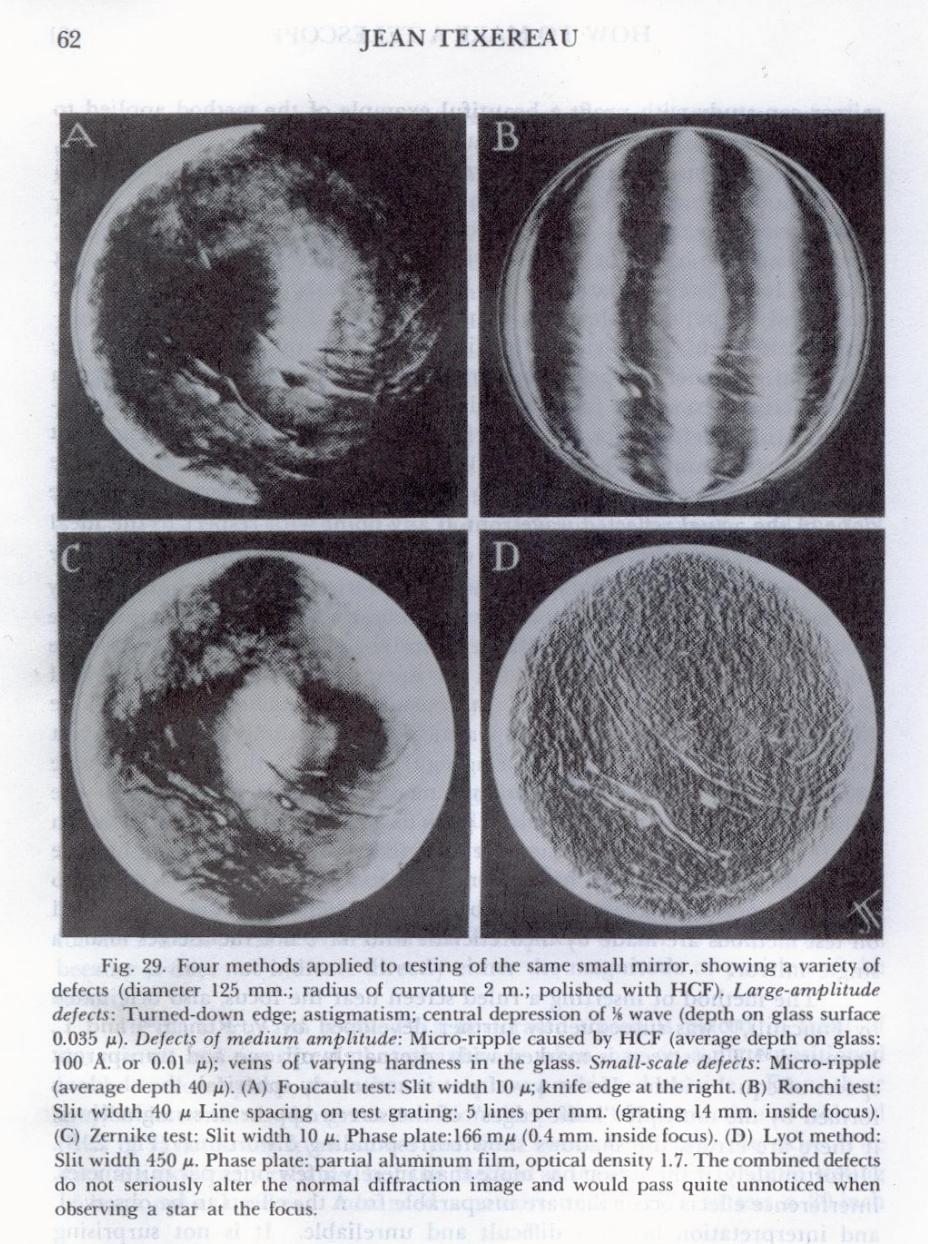




##############################################################################
Der Spiegelschleifer Kurt hat hier folgendes verlautbart:
http://www.astrotreff.de/topic.asp?TOPIC_ID=64847
Quote:
Bisher hat noch niemand überzeugend nachweisen können, dass sich der Unterschied von "extrem geringer Rauheit" zur "normalen" Rauheit von Spiegeloptiken bei der Beobachtung bemerkbar macht. Dazu müsste erst mal definiert werden was denn extrem gering und was normal ist. Mit traditioneller Pechpolitur schafft man ohne große Mühe Rauheiten der Wellenfront von weit besser als 1/100 RMS lambda. Lt. Schroeder "Astronomical Optics" folgt daraus ein Abminderungsfakor für die Kontrastübertragung von 0,996. Einfacher gesagt, der Bildkontast würde wegen Rauheit schlimmstenfalls um 0,4% gemindert. Sehr wahrscheinlich machen sich Restfehler in Form von Zonen, sphärischer Aberration, Astigmatismus ect. eher bemerkbar, selbst bei sehr guten Spiegeln. Sinngemäß kann man das auch bei Suiter "Star Testimg Astronomical Telescopes" nachlesen.
Vor einigen Jahren hab ich einen Artikel von Zambuto gelesen indem er behauptet hatte, nur er würde Spiegel extrem glatt polieren. Amateuren z. B. sei dies gar nicht möglich, weil sie die beim Schleifen entstandenen Mikrorisse nicht auspolieren könnten. Er kann wahrscheinlich für sich im Anspruch nehmen, dass seine Spiegel statt der oben geschätzten 0,4% nur 0,04% Streulicht wegen Rauheit produzieren.
Dazu ist folgendes zu sagen:
- Dieses Thema wird sich akademisch weniger lösen lassen, und schon gar nicht über die Literatur.
- Die "Rauhheit" einer Optik meint nicht deren Topografie, also nicht die "Landschaft" der Wellenfront. Sie meint die Flächen-Feinstruktur, die mehr oder weniger Streulicht erzeugt und über obere Bilder über den Lyot-Test nachweisbar ist.
- Bei der Frage der Rauhheit muß man ganz streng unterscheiden, ob man ein Teleskop visuell oder fotografisch nutzen möchte. Bei der visuellen Benutzung spielt die Rauhheit - auf welche Art sie immer entsteht - eine ganz zentrale Rolle. Bei der fotografischen Benutzung spielt die Rauhheit nahezu keine Rolle.
- Die visuelle Nutzung ist sehr viel schlechter zu dokumentieren als die fotografische Nutzung. Da werden selbst Feldaufnahmen mit schlechten Optiken noch beeindruckend.
- Das Orion-Trapez ist aber ein sehr guter Indikator für rauhe oder glatte Spiegel-Optiken. Wenn man die Komnponente E und F exakt definiert erkennen kann, hat man es mit einer sehr glatten Spiegel-Optik zu tun. Ein "rauhes" System verschluckt diese feinen Sterne.
Dies kann man aber nur im direkten Vergleich in der Beobachtungs-Praxis nachweisen und leider schlecht dokumentieren.
Der höhere Kontrast bei einem Refraktor (APO) hängt auch damit zusammen, daß über die Refraktion von Licht durch die Linsen weniger Streulicht verursacht wird, was wiederum sehr gut über den Lyot-Test nachweisbar ist, wenn man die vielen Beispiele auf meiner Index-Seite einmal anschaut.
http://r2.astro-foren.com/index.php/de/berichte/03-newton-systeme-und-verwandte-fragen
Vergleiche diese Übersicht mit der oberen Übersicht.

http://homepage3.nifty.com/cz_telesco/refracter_test.htm
http://homepage3.nifty.com/cz_telesco/newton_test.htm
E047 Kompensation durch Linse und Sphäre
Kompensation durch Linse oder gegen Sphäre
Ein wunderbares Spiegelschleif-Ergebnis!
Es begann damit, daß ein Spiegeldurchmesser von 210 mm zwar gegen einen Planspiegel mit 80 mm Bohrung
geprüft werden kann, von der Spiegelmitte aber nicht mehr viel zu sehen ist. Es könnte hinter der Bohrung in
der Mitte ein "Zuckerhut"ebenso versteckt sein, wie eine deutliche Mulde, die dann nur zum Teil vom ellipt.
Fangspiegel verdeckt werden würde. In einem solchen Fall bieten sich eine Plankonvex-Linse oder ein Kugel-
spiegel als Kompensations-Möglichkeit an, weil bei einem Null-Test die Fläche über ein Interferogramm, den
Roucault- und Ronchigitter-Test als Gesamtfläche eingeschätzt werden kann. Auch der Test gegen einen
Kugelspiegel (Sphäre) ist möglich. In diesem Fall steht jedoch die Lichtquelle bzw. der BathInterferometer
im Strahlengang zwischen den Spiegeln und verdeckt ähnlich wie bei der Autokollimations-Anordnung einen
zentralen Teil in der Mitte. Man vermeidet in diesem Fall aber das sekundäre Spektrum der Plankonvexlinse,
braucht aber weitere Hilfmittel, um an den Fokus des Prüfaufbaues zum kommen.
Siehe auch http://rohr.aiax.de/dall-0.jpg, http://rohr.aiax.de/hubble09.jpg, http://rohr.aiax.de/hubble09a.jpg
Die Kompensationsrechnung war über ZEMAX bereits vorbereitet und mußte nach einem exakten Vermessen vom Radius
nur noch aktualisiert werden. Das Spotdiagramm hat in diesem Fall einen geometrischen Durchmesser von 0.1 Mikron
und der Strehl liegt nahezu bei 1. Dem Datenblatt kann man den Testaufbau entnehmen. Die Restfehler, die über diesen
Testaufbau eingeführt werden, sind also verschwindend gering.
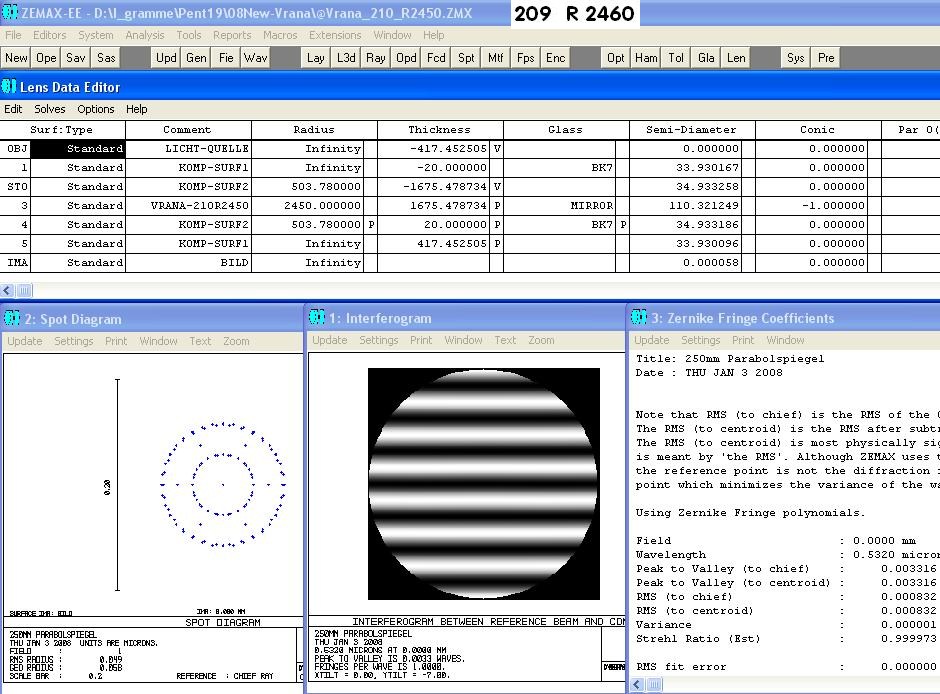
Der Spiegel selbst war noch unbelegt, was aber kein Problem ist, wenn nicht gerade die Rückseite blank poliert wäre.
In diesem Fall hätte man es mit Fremdlicht zu tun, was das Interferogramm empfindlich stören kann. So steht einer
wie immer gearteten Kompensations-Messung nichts im Wege. Würde man hingegen einen Planspiegel benutzen, dann
käme auch ganz wenig Licht wieder zurück, weil das Lichtbündel den unbelegten Spiegel zweimal passiert.

Ein ganz wichtiger Test zu Beginn ist der TEst auf Rotations-Symmetrie, eigentlich ein Ausschlußtest für Astigmatismus.
Da ja auch über den Meßaufbau bzw. der Spiegellagerung Astigmatismus eingeführt wird, kann man im Vorfeld klären,
ob in RoC ein signifikanter Astigmatismus vorhanden ist, den man berücksichtigen muß, oder ob man den Astigmatismus
vernachlässigen kann, nachdem man am Himmel selbst einen L/3 PV Astigmatismus kaum wahrnimmt. Im konreten Fall
kann man also den Astigmatismus vernachlässigen und deswegen abziehen.

Mit einer 210 mm Durchmesser Plankonvex-Linse ist eine Form der Kompensation möglich. Das Sekundäre Spektrum der
Linse selbst muß man mit einem engen Interferenzfilter auf 550 nm eingrenzen, was sich über den Solar Continuum Filter
von Baader sehr gut lösen läßt.

Verfolgt man hingegen die Compensation über einen Kugelspiegel, dann hat man das Farbproblem nicht, dafür steht aber
der Bath-Interferometer im Strahlengang und verdeckt einen Teil der Spiegelfläche, wie man auf dem entsprechenden
Interferogramm (übernächstes Bild) erkennt. Das Kompensationsprinzip bleibt gleich: Lichtquelle-Sphäre-Parabel-
Sphäre-Messerschneide. Um an das Testbild zu gelangen, genügt ein kleines Keplerfernrohr, umgekehrt verwendet und
da mit niedriger Verkleinerung. Über die Optikrechnung bekommt man auch den jeweiligen Bündeldurchmesser, wenn man
in der Bildebene eine Dummy-Blende einführt.

Im IGramm erkennbar der Haltestift und den Bath-Interferometer. Das Interferogramm stammt aus einer Kompensation
Kugelspiegel/Radius 2368 mm gegen einen 300/1500 Newtonspiegel.
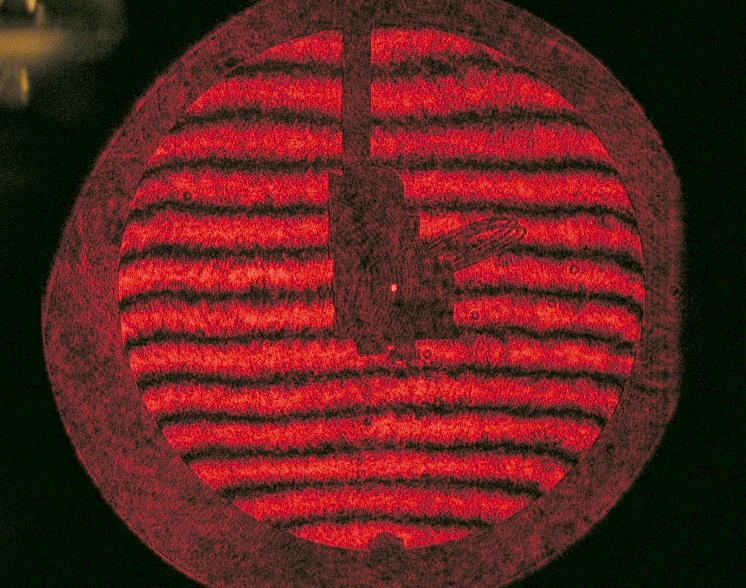
Im folgenden Beispiel wurde die bereits oben gezeigte Plankonvex.Linse verwendet.

Massimo Ricardi hat auf meinen Wunsch hin in AtmosFringe eine ganz entscheidende Neuerung eingefügt. Bei der
Beurteilung der Streifenbilder besonders derer aus dem RoC (Krümmungsmittelpunkt) hat man das Problem, wie man den
Verlauf der Streifen interpretieren soll. Für diesen Fall ist eine Bezugslinie oder das ideale Interferogramm sehr wertvoll,
weil man den IST-Stand mit dem Soll-Stand vergleichen kann. Man kann mit diesem Hilfmittel klar erkennen, an welcher
Stelle der Spiegel retouchiert werden muß: Weichen die IST-Streifen nach oben ab, muß genau an diesen Stellen
noch Glas wegretouchiert werden, den nach unten abweichenden Bereich läßt man möglichst in Ruhe.

Da die Justage der Testanordnung mit einem Laser sehr schnell und unkompliziert verläuft, hatten wir sofort ein
auswertbares Interferogramm, mit einem sehr ansprechenden Ergebnis.
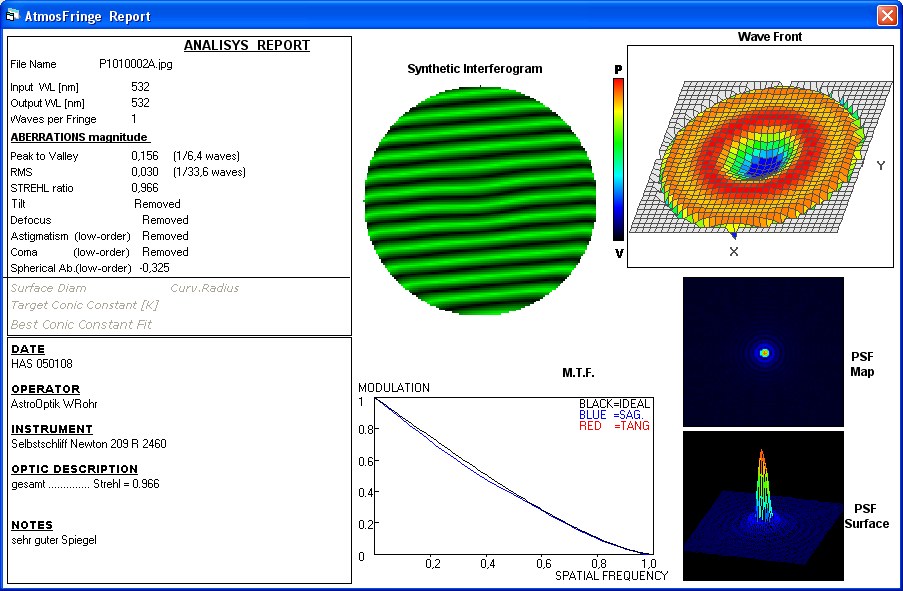
Auch über den RoC Gegenbeweis entstand nahezu das gleiche Strehlergebnis.
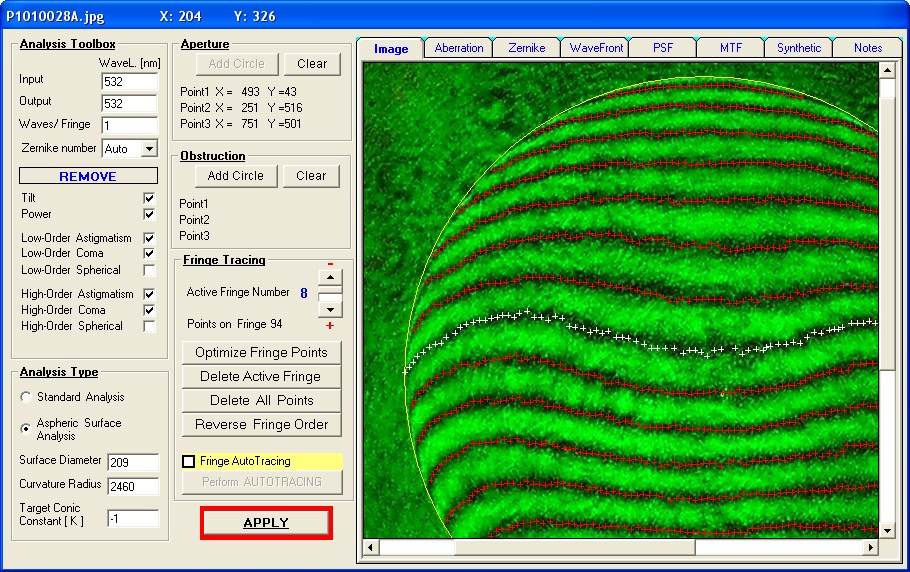
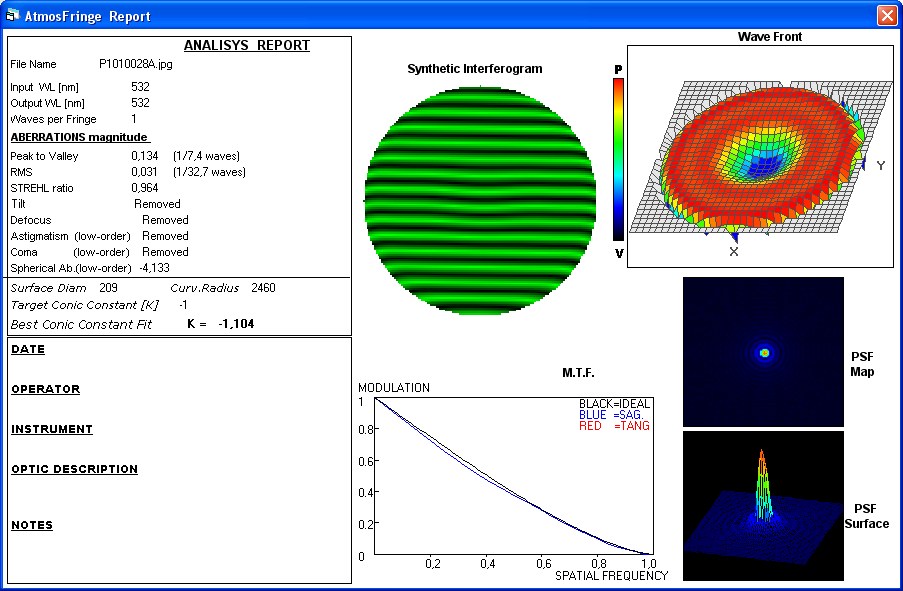
Bei der Kompensation mit einer Linse sind der Foucault- und der Ronchi-Gitter-Test ebenfalls möglich, solange man einen
engen Interferenzfilter verwendet. Beide Tests zeigen, mit wieviel Sachverstand und Liebe der Sternfreund seinen
Spiegelgeschliffen hat. Ein Umstand den ich nur positiv würdigen kann.

Die schnurgeraden Ronchi-Linien haben mich besonders begeistert. Ich habe aus meiner Anerkennung kein
Hehl gemacht.
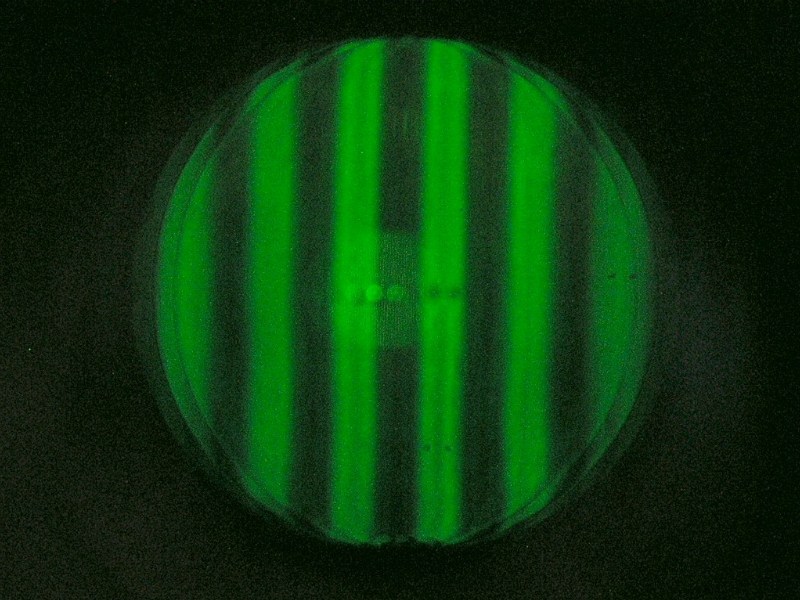
Weitere Bilder zur Kompensation gegen Sphäre

Fringe Map between the mirrors

Die Einheit Bath-Interferometer

Das gesamte Bauteil

Der Spiegel under test

Die Kompensations-Sphäre

#######################################################################
this Waineo-Test would work. This is just the setup in ZEMAX. Later I try to calculate your system.
This test is a one-way-test, and you just can test with Ronchi and Foucault as null test.
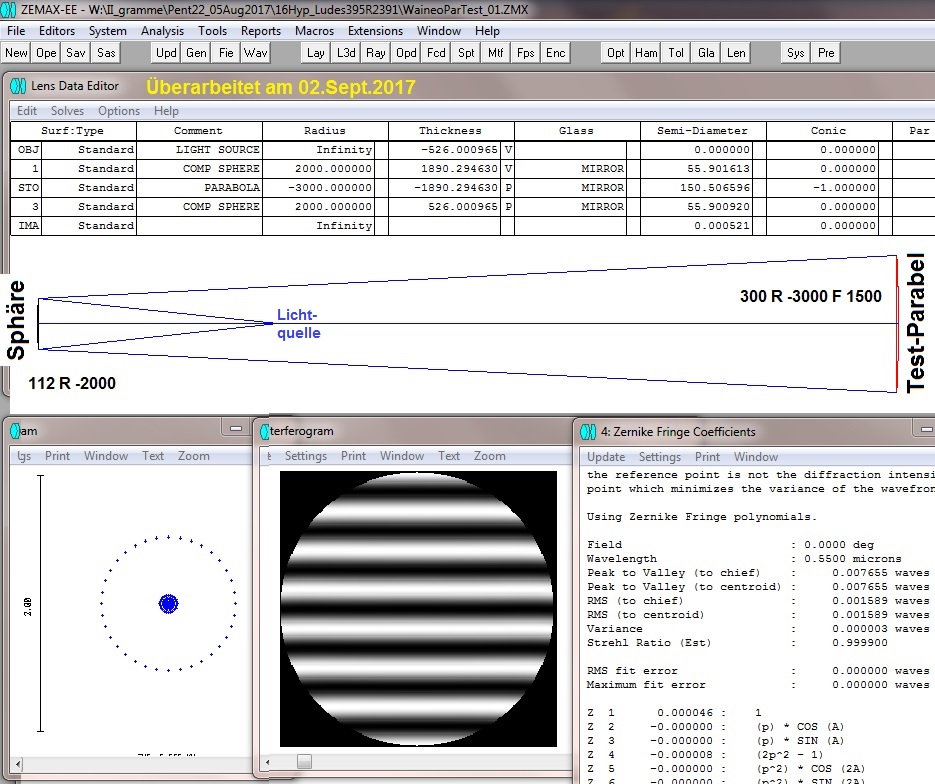
########################################################################
Dear Franck,
you hole in the sphere is to small. I should be 50 mm and more. Now I insert values similar as yours. If the
hole is to small, the distance mirror-focus must be small for the 30 mm sphere hole, but for this the sphere
diameter must be larger. But if the whole is bigger, better 50 mm, so the sphere diameter becomes smaller.
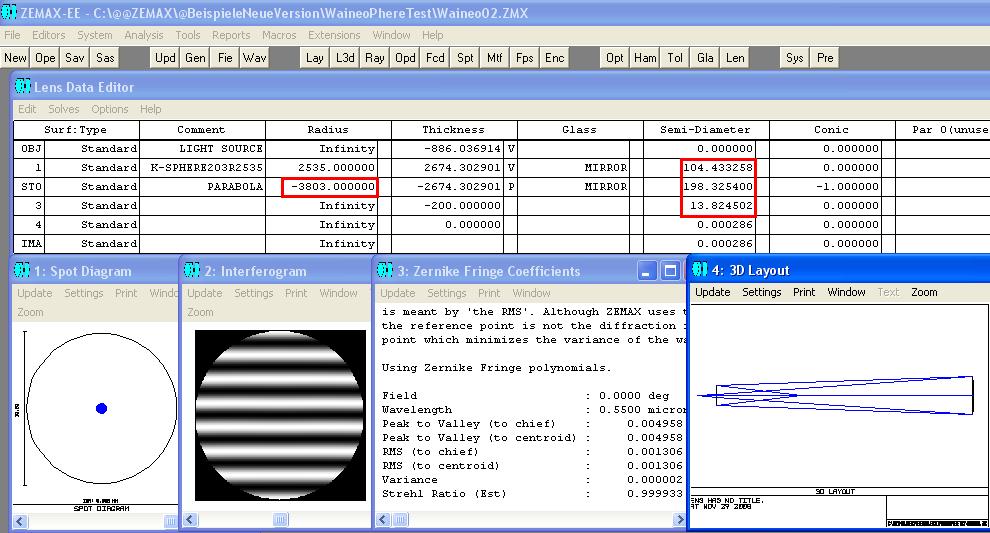
a second example with the values of your program waineo2006.zip
calculated with ZEMAX:

##########################################################################
Dear Franck,
Waineo: with 150 mm distance from the sphere surface the focus is very closed to handle any test, but it is possible.
Now the setup with your sphere 2535 and the parabola 400 R 4000: If you use an ellipt. flat, you have an
alligne problem, be sure. But her this could be the solution: http://rohr.aiax.de/ParabelSphere02.jpg
In that case the flat should be as small as possible about 30 mm, because the light cone at that position
is about 198 mm in diameter, and so you need about 100 mm outside the light cone and more. Good luck!

E046 Oldham Spiegel - Rayleight Water Test
http://www.oldham-optical.co.uk/news.htm
Oldham Spiegel, eine lange Geschichte.
Oldham Spiegel prüfe ich schon lange. Und nachdem sie andernort auch
schon mit dem ZYGO unter ähnlichen Merkmalen vermessen werden, möchte
ich zur oberen Webseite einiges an Information beisteuern, zumal einer
unserer Händler genau auf dieses Ritchey-Chretien-System wartet, weil
er es verkaufen möchte. Man kann der Sache eigentlich nur gutes Ge-
lingen wünschen. Ich habe nun mehrere Versuche hinter mich gebracht,
mich mit Oldham einfach intern über Meßtechnik auszutauschen - nicht
alles muß ja gleich in aller Öffentlichkeit breitgetreten werden. Der-
artige durchaus gutgemeinten Versuche stießen aber bei Norman nicht
unbedingt auf seine Gegenliebe, obwohl ich immer wieder Anfragen für
große Spiegel habe, und Oldham durchaus eine Adresse wäre, wenn man
an ihn heran-käme.
Zum Bild "News_SDAS Group2":
Aha, endlich mal ein Bild von Norman Oldham, links. Interessieren
würde mich der Autokollimations-Flat wegen dessen Größe. Die Lagerung
des hyperbolischen Hauptspiegels halte ich bei derart dünnen Spiegeln
für kritisch, und es sollte eine Schlingen-Lagerung sein. Ansonsten
ist Holz auch in England ein beliebter Werkstoff, Muliplex ist es aber
offensichtlich nicht. Die Meßeinrichtung selbst ist offensichtlich Betriebs-
geheimnis (?) !!!
Zum Bild "News_SDAS Group3":
Exakt wäre diese Art Flat-Messung nicht. Es fehlen sowohl die Kondensor-
Linse, die ein paralleles Bündel erzeugt, weil das schiefe Hineinschauen
die Interferenz-Streifen verändern kann. Bei Bugiel schaut das so aus:
http://www.optikpraxis.de/
Das sind Beispiele für den Fizeau-Interferometer zum Prüfen von Planflächen.
Prinzipiell wäre der Aufbau so:
====================================================
Hier scheint ein sachlicher Irrtum vorzuliegen:
Quote:
I believe there is some misunderstanding regarding the "Strehl
Factor" in the specification of optical components. I will attempt to
explain what this means regarding concave reflectors in Newtonian
telescopes.
The Strehl Factor calculates all errors that exist on a optical surface
of this type of reflector. It includes:-
Der Strehl errechnet sich aus den Fehlern der ankommenden Wellenfront,
wie sie über ein Interferogramm in Autokollimation entsteht und bezieht
sich damit auf die Wellenfront und eben nicht auf die Oberfläche. Natür-
lich können die Wellenfront-Fehler mit dem Faktor /2 auf die Oberfläche
umgerechnet werden. Das macht aber nur bei einer opt. Fläche einen Sinn,
bei einem System kann man nur die ankommenden Wellenfront messen und
untersuchen und erst im zweiten Anlauf untersuchen, welches Bauteil für
welchen Fehler verantwortlich ist.
The Conic shape oder bei uns die Conische Konstante sagt nur etwas
über die Korrektur der Fläche aus: Nicht jedoch über die sphär. Aberration
oder sonstige opt. Fehler.
Also sphärisch = 0
Ellipse . . . .= { 0 > X > -1}
Parabel . . . .= -1
Hyperbel. . . .= {-1 > X > unendlich}
Man kann sie in Kompensation über eine Sphäre messen und bestimmen.
Der Astigmatismus wird über einen künstlichen Stern gemesssen, über
einen Drahttest oder mit einem beliebigen Interferometer sehr genau gemessen.
Surface "smoothness" or "roughness"
===================================
Hier scheiden sich offenbar die Geister ganz erheblich.
Quote:
The dominant error in any mirror from a professional mirror
maker is always P-V. Astigmatism and "Smoothness" are always extremely
low in comparison.
Das mag die Begründung sein, warum Oldham Spiegel einerseits sehr rauh,
und vor allem recht häufig einen signifikanten Astigmatismus haben. Ein
weiteres Merkmal sind häufig vorkommende starke Unterkorrektur und einen
immer wieder zu beobachtenden "Kegel" in der Mitte von bis zu 1.5 Lambda
der Wellenfront und mehr. Bei einem RC-System kann man diesen Kegel
wegbohren, aber bei seinen Newton-Spiegel werden sie manchmal nicht
völlig vom Fangspiegel verdeckt und sind nur bei diesem Hersteller festzu-
stellen.
Quote:
There have been a number of Incidents in the last year where
feedback on an Oldham Mirror has suggested that although the Mirror
has a P-V to specification and a Strehl to specification, the mirror
is not "smooth". This is usually an opinion we receive "second hand"
from a third party Mirror Tester using an interferometer showing
pictures of "Contrast". When we have asked for numerical quantification
of the perceived lack of "Smoothness", there has never been any
figure offered.
Es ist nun Sache von Norman Oldham selbst, wie er sich auf seinen Web-
Seiten darstellt. Und wenn er Testern, bei denen er nicht so gut weg-
kommt, in ein schiefes Licht rückt, dann kann man das auch noch ver-
stehen.
Dieser Konflikt läßt sich jedoch sehr leicht ausräumen, indem er seine
Spiegel mit einem ZYGO vermessen läßt, was ja in Wirklichkeit immer
wieder passiert. Das ist also mein sehr ernst gemeinter Vorschlag,
und ich hätte da mehrere Kandidaten, die ich ins Rennen schicken
könnte:
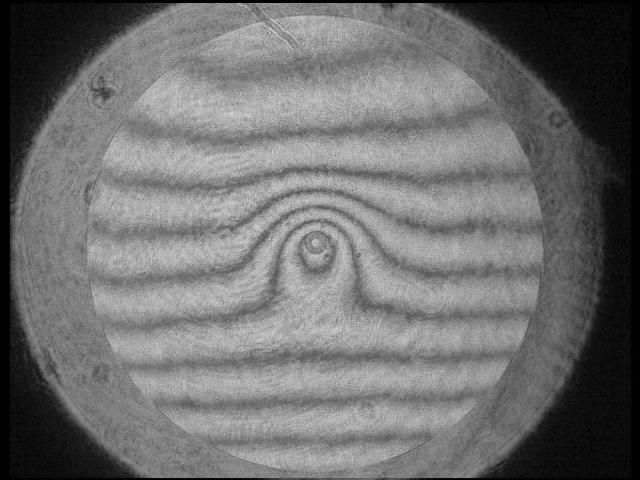
Dieser Kandidat liegt mindestens 2 Lambda der Wellenfront daneben,
und zeigt einen deutlichen Astigmatismus.

Mit 127 mm reicht dieser Kegel ganz schön in die Spiegel-Fläche hinein,
und der Kunde war wieder nicht zufriedenzustellen. Insgesamt beachtliche
drei Male. Der arme deutsche Händler tat mir in diesem Zusammenhang
eigentlich leid.

Ein anderer Kandidat hat wieder diesen "Kegel" und natürlich ebenfalls
Astigmatismus.
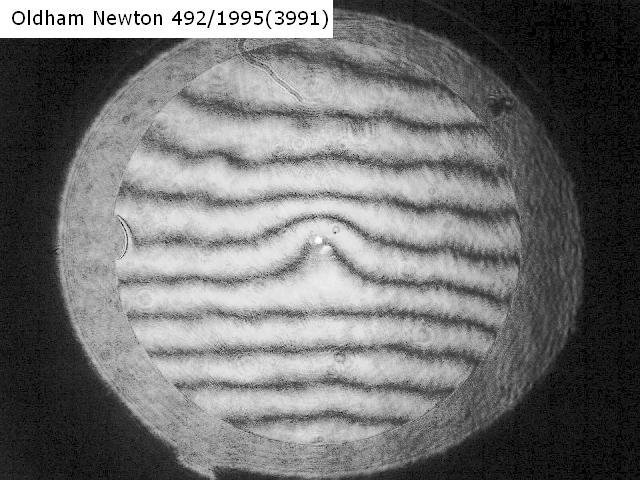
#######################################################################
Hallo Argus,
Nähe Venedig gibt es einen Hersteller, dessen Optiken man vor Gebrauch über-
prüfen lassen sollte. Ich bin mir aber nicht sicher, ob diese Firma
http://www.reginato.it/index.html mit dem vorgenannten Hersteller etwas
zu tun hat. Der hieß anders. Viele kleinere Hersteller gehen scheinbar davon
aus, daß der normale Sternfreund bei uns seine jeweiligen Optiken ohnehin
nicht einschätzen kann - einen Eindruck, den man oft bekommen kann, wenn
man manche Äußerungen so liest.
Bei Oldham würde ich mir wünschen, daß zumindest intern und damit nicht-
öffentlich ein Kontakt möglich wäre. Das ist aber bereits in England selbst
ein Problem. Dort wird, genauso wie bei uns, häufig nachgemessen ! ! !
E043 Rayleight-Water-Test Pent14-250-FlatNeuM
Der Rayleigh Water Test
In der Literatur ist er hinreichend bekannt. Das National Bureau of Standards und das britische National Physical Laboratory
haben auf diese Weise früher ihre Referenzplanflächen getestet. Zu dem Test gibt es ferner einen Artikel des letzteren Labors
in British Science News 2, 130 (1948). In der Testapparatur dieses Labors diente eine 38 cm Plankonvexlinse aus Kriegs-Über-
beständen ("surplus") als Kollimator, an welchen (-> Malacara) an sich keine übermässig grossen Anforderungen gestellt werden.
Im Artikel von Sky&Telescope kommen sogar Fresnellinsen zum Einsatz.

Nun ein paar Erfahrungen im Umgang mit dem Test:
01. Man muß unbedingt die Boden und Raumschwingungen abkoppeln,
also schraubte ich die Apparatur an die Wand.
02. Das Wasser muß erstens sauber und frei von Schwebeteilchen sein
und ganz zartfühlend mit Spülmittel entspannt sein, aber so, daß
keine Blasen entstehen. Also einen Tropfen davon anrühren in einem
eigenen Gefäß und dann ohne Blasen 2-3 cm^3 ins "Prüf"-Wasser gießen.
03. Der Glaskörper ist vollständig in Wasser eingetaucht.
04. Weil die Kohärenzlänge meiner Hochdruckdampflampe sehr kurz war,
war die Dicke der Wasserschicht über der Glasfläche bei ca. 1 - 1.5 mm
05. Die Justage der Glasfläche zur Wasserfläche ist diffizil, in
meinem Fall über eine 3-Punktauflage und 3 M6-Stellschrauben mit
1 mm Gewindesteigung. Es sind Bewegungen im Micron-Bereich und viel
Geduld nötig.
06. Im Brennpunkt der Kondensor-Linse hatte ich einen hellen
Lichtpunkt, den ich durch die Reflexion der Wasser- und Glas-
oberfläche zunächst doppelt sah. Durch die Justage des Wasser-
behälters blieb zwar das Wasser weiterhin genau in der "Waage"
aber die Glasfläche bewegte sich, und dadurch konnte man die
beiden Reflexbilder zur Deckung bringen und erhielt die bekann-
ten Interferenzstreifen. Eine falsche Bewegung, und das Ver-
gnügen begann erneut.
07. Eine Wasseroberfläche ist opt. das Genaueste, was man sich
wünschen kann und liegt in der Gegend von L/300 PV wave für
einen Durchmesser von 250 mm. Kann man aber ganz exakt rechnen.
Tyho Brahe hat mit der Wasseroberfläche seines Brunnens seine
Sternörter bestimmt: http://de.wikipedia.org/wiki/Tycho_Brahe
Die Prüfung von Planflächen gegen Flüssigkeits-Oberflächen wurde
schon oft beschrieben. Man kann Öl ebenso benutzen, wie Queck-
silber.
#############################################################################
Dear Franch and Uwe,
Normally the quality of the plan convex lense isnot important. The lens
I use is'nt polished correctly, but it doesn't matter. You just need a
parallel light beam for this test and back.
The last day, I repeated this water test with a 250 mm flat with a
hight surface accuracy but many, many scratches. It must have been
a reference flat from any interferometer. I noticed that the light
coherence lengh is very important. If you use monochromatic light,
the water film on top the uncoated flat glas surface must be very
thin. And then water is moving like oil, very slowly.
If you use a laser light with a glas bowl of 2 mm then the water film
can be some millimeter, but then the water flat surface is very turbulent. To get interference fringes I use a laser beam and bring the
reflexes from the two surfaces togehter and then it starts with
fringes. The third foto is the artificial star for aligning the water
surface with the glas surface - it's tricky.




############################################################################
Das Prüfen gegen eine Wasser-Oberfläche ist eine spannende Angelegenheit, besonders bei
einem Durchmesser von 250 mm. Die Prüfkammer hängt schon deswegen an der Wand, um
sie vor den Bodenschwingungen abzukoppeln - ganz läßt sich das aber nicht ausschalten.
Die unbeschichtete Glasfläche interferiert mit der Wasseroberfläche nur, wenn beide Flächen
nahezu parallel sind bei Abweichungen von ca. einem Micron. Zur Justage kann man die
Reflexbilder von beiden Flächen nehmen und sie zur Deckung bringen. Von der Kohärenz-
Länge der monochromatischen Lichtquelle wiederum hängt es ab ...Quote:
Die Kohärenzlänge ist der maximale Weglängenunterschied, den zwei Lichtstrahlen,
die derselben Quelle entstammen, haben dürfen, damit bei ihrer Überlagerung noch ein
Interferenzmuster entsteht. Die Kohärenzlänge kann entweder in einem Längenmaß
ausgedrückt werden, dann bezeichnet sie den Gangunterschied der beiden Teilstrahlen
oder als Zeit, dann ist die Laufzeitdifferenz der beiden Strahlen gemeint.
Lichtquellen mit einer großen bis sehr großen Kohärenzlänge (einige Millimeter bis viele
Kilometer) sind beispielsweise Laser. Weißes Licht wie Sonnenlicht hat generell eine sehr
kurze Kohärenzlänge von nur wenigen Mikrometern.
... wie dick der Wasserfilm über der Glasfläche sein darf. Beim Licht einer
Natrium-Dampflampe, deren Kohärenzlänge sehr kurz ist, klappt es nur mit einem max.
1 mm dicken Wasserfilm, und der wiederum benimmt sich wie Öl und man sieht das
Wasser die Kanten "herunterfallen" Hier reagiert das System träge und schnelle Wasser-
wellen/Schwingungen sind sind möglich. Bei der Kohärenzlänge eines Lasers mit mehreren
Metern hingegen darf zwar die Dicke des Wasserfilmes sehr viel stärker sein, dafür tauchen
aber alle Bewegungen/Schwingungen auf, die auf das Wasser aus der Umgebung einwirken,
also auch ein vorbeifahrendes Auto bei 30 m Entfernung. Möglicherweise ist Öl ein besseres
Medium als Wasser, was ich vermutlich ebenfalls ausprobieren werde. Da wird auch eine
größere Kohärenzlänge möglich sein.
250 mm Flat-Gesamtdurchmesser gegen eine Wasser-Oberfläche geprüft (mit Spüli entspannt)
Gegen eine Referenz-Fläche geprüft, macht die Planfläche einen sehr guten Eindruck, meine Referenzfläche hat
laut Rucks-Certifikat PV L/20 der Wellenfront, und dieses würde man im Streifenbild auch noch sehen. Geprüft mit
einer Natrium-Dampflampe.


Die 250 mm Planplatte muß als Referenz-Fläche aus einem Interferometer stammen.
###############################################################################
Hallo Thomas,
uns beiden jedenfalls gehört die Platte nicht. Die stammt aus dem Billig-Optik-Laden aus USA: http://www.surplushed.com/
und der glückliche Besitzer wollte wissen, wie gut das Teil ist.
Habe dafür eigens meinen certifizierten 165 mm Planspiegel abgelaugt und ausgiebige Wasser-Tests gemacht. Ich hätte ja
noch einen Planspiegel gleicher Größe hier, den ich auf diese Weise auch untersuchen könnte. Jedenfalls die Methode mit
einem Kugelspiegel scheiterte nahezu an der verkratzten Oberfläche des 250 Flat. Die beiden Planflächen haben zuein-
ander eine nur geringe Neigung, weshalb bei grünem Laser-Licht solche Interferogramme herauskommen:

E042 Test im einfachen Durchgang mit einem Newton-Spiegel
Prüfaufbau: einfacher Durchgang . . . (Erzeugung eins parallelen Lichtbündels)
. . . Für alle diejenigen, die keinen großen Planspiegel haben, aber einen genauen Parabolspiegel größer/gleich 30 cm.
Einen hochwertigen, glatten Planspiegel zu bekommen, ist schwierig und zudem teuer und dann weiß man immer noch nicht so
richtig, wie genau er dann tatsächlich ist. Für diese Fälle gibt es eine Lösung, die bei sorgfältiger "Zubereitung" zu ähnlich guten
Aussagen führt, wenn man die Qualität von Optiken überprüfen will. Allerdings nur qualitativ, für eine quantitative Auswertung
wird man weiterhin die Autokollimations-Testanordnung benutzen müssen, und dann geht es nicht ohne Planspiegel.
Das Prinzip besteht darin, daß man in den Fokus eines genauen Parabolspiegels eine 20µ Pinhole oder einen 10µ Lichtspalt
setzt - exakt auf der Achse. Damit hätte man ein paralleles Lichtbündel (aus dem Unendlichen) Die genaue Brennweite ermittelt
man über den halben Radius des Spiegels auf der Achse und dann hilft ein Laser-Pointer und ein Bandmaß bei der Einrichtung des
Testaufbaues weiter. Mit diesen Hilfsmitteln kommt man sehr nahe an das Ideal heran. Die linke Parabolspiegelseite wird zwar
durch die Halter verdeckt, die rechte jedoch ist bis zu einem Durchmesser von HauptspiegelDurchmesser/2 für Messungen frei, wie
die Skizze zeigt.

Von dort, wo später der Prüfling steht, schaut der Sachverhalt dann so aus:

Die linke Seite wird über diverse Halterungen verdeckt, die rechte Seite ist frei für Messungen. Die Meßgenauigkeit erhöht sich
deswegen, weil nur der schraffierte Teil des Spiegels benutzt wird, während sich Genauigkeits-Angaben auf den gesamten
Newton-Spiegeldurchmesser beziehen. Zonen sollte der Parabolspiegel allerdings keine haben, die würde man beim Foucault-Test
sehen.

Der Aufbau der Pinhole ist hier etwas beschrieben: http://www.astro-foren.de/showthread.php?t=5818 Die Halterung aus
MultiPlex berücksichtigt noch eine Höhen-Verstellung. Ein heller grüner Laser wird auf die Mitte des Parabolspiegels gerichtet und
in sich zurückreflektiert. Im Abstand des Spiegel-Fokus wird die Pinhole eingeschoben und zentriert, indem man den Laserpunkt
auf der Rückseite der Messing-Halterung verfolgt.

Wenn der künstliche Stern in Okularmitte zu finden ist, wäre auch der Prüfling auf der Achse - in diesem Fall wäre dieser Testauf-
bau für den kleinen Tak hinreichend groß.

Durch den Tak kann man sich dann bei niedriger Vergrößerung den künstlichen Stern 20µ mit Halterung, Prisma etc. betrachten.

Und das wären zwei der 3 Test-Möglichkeiten: Ronchi, Sterntest und Foucault. Bei Foucault wäre ein Lichtspalt als Licht-
quelle sinnvoller, ebenso beim Ronchi-Test; ein Interferogramm ist bei dieser Testanordnung leider nicht möglich.
Die Anordnung läßt sich in der Weise auf Unendlich "eichen" indem man mit einem Test-Fernrohr am Himmel auf Unendlich ein-
stellt. Diese Einstellung fixiert und den Fokus-Punkt zum Parabolspiegel solange verschiebt, bis auch dort die gleichen Einstellung
zu erkennen ist. Mit einer Eich-Linie mißt man dann den Abstand zur Spiegelkante bzw. Spiegelrückseite aus. Mit diesem Wert
läßt sich dann diese Einstellung immer wieder reproduzieren, wenn man die Komponenten nicht gerade fixieren will. Die Lage der
Pinhole muß natürlich ebenfalls immer wieder die gleiche sein.

E039 RossNull Kompensation versus RoC
Kompensation versus RoC/Radius of Curvature
Dieser Thread schließt an diesen Bericht an: http://www.astro-foren.de/showthread.php?p=31851#post31851 Mit hoher
Perfektion wurde dieser Spiegel, an den der Sternfreund große Erinnerungen knüpft bzw. sein Herz hängt, von Orion Optics,
UK, zu einem perfekten Newton-Spiegel umfiguriert und natürlich neu mit Hilux belegt. Ein Zygo-Certifikat lag auch dabei,
weswegen für mich die Sache noch einmal sehr interessant wurde. Da ein Zygo aus dem Krümmungsmittelpunkt mißt, ist
der Versuch, ebenfall in RoC ohne Kollimations-Spiegel im einfachen Durchgang zu messen für den Spiegelschleifer-Ama-
teur oft die einzige Möglichkeit, seine Spiegel zu testen, wenn er nicht gerade den Test am Himmel vornimmt, das ist
dann die sicherste Lösung. Bei diesem Test hat man grundsätzlich einen Lagerungs-Astigmatismus, dessen Größe man
auf unterschiedliche Art erfassen und herausrechnen kann.

Beim Zygo werden in der Regel aus mehreren hundert Einzelmessungen ein Durchschnitts-Ergebnis ermittelt. Da wäre ein
Amateur zeitlich etwas überfordert. Schaut man aber im Certifikat die 3-D-Darstellung genauer an, dann würde man
an diesem Bild eine leichte Überkorrektur erkennen, trotz eines Strehls von 0.99: Wir erkennen in der Mitte eine leichte
Vertiefung, bei ca. 50% Radius einen leichten Wall, und zuletzt würde der Rand gering-fügig aufstehen. Diese Merkmale
sind bei allen meinen Messungen ebenfalls zu finden.

Ausgehend von diesem Bericht war der Spiegel bei einer konischen Konstanten von -0.24 erheblich zu zaghaft parabo-
lisiert, also fast noch ein Kugelspiegel, der wenn man in auf der Rückseite gut isoliert, ganz automatisch in die Parabel
fällt bei fallenden Temperaturen in der Nacht. Es kamen also bei der ersten Messung nur 0.476 Strehlpunkte heraus,
verursacht durch die Unterkorrektur und gut sichtbar in der 3-D-Darstellung rechts.

Nun hat die RoC-Methode deswegen ihre Tücken, weil sie nur funktioniert, wenn (1) der Radius exakt bekannt ist,
ebenso der (2) optisch wirksame Durchmesser, wenn das Interferogramm (3) kantenscharf den Rand abbíldet, und das
Interferogramm möglichst (4) kontrastreich ist, damit das Auswert-Programm damit etwas anfangen kann und nicht
gerade eine (5) Luftschliere einen Astigmatismus vortäuscht.
Eine abfallende Kante wird ein solches Interferogramm nur dann abbilden, wenn sie deutlich ausgeprägt ist, auch die Frage der Unter- bzw. Überkorrektur wird nicht sicher damit beantwortet - das hängt bereits wieder vom richtigen RoC-Radius und dem opt. wirksamen Durchmesser ab. Also sehr viele Parameter, die man exakt einhalten muß. Deshalb ist
ein Sterntest am Himmel besonders bei großen Spiegel-Durchmessern am sichersten.
Eine weitere Testmöglichkeit bietet das Kompensations-Setup (ähnlich dem Dall-Null-Test) entweder wie in meinem
Fall durch eine Plankonvex-Linse oder gegen eine Sphäre. Bei der Sphäre müßte man zwischen den beiden Spiegeln prüfen, bei der Plankonvex-Linse schaltet man eine EinzelLinse dazwischen, von der man aber die opt. Daten ganz exakt
haben muß, wie in meinem Fall. Bei der Einzel-Linsen-Kompensation ist ein Interferenz-Filter für exakt eine Wellen-
Länge erforderlich, in meinem Fall der Baader'sche Solar Continuum Filter hier mit Transmissions-Kurve. Jetzt muß das
System nur noch "geeicht" werden auf die Meß-Wellenlänge von 532 nm wave: Gesucht ist der Brechungs-Index für
die ZEMAX Rechnung, der bei allen künftigen Simulationen dann gleich bleibt.
Mit diesen Daten kann man dann mit ZEMAX, Oslo oder Atmos ... den Abstand zwischen Spiegel und Linse einstellen, der
Abstand der Lichtquelle zu Linse ergibt sich dann automatisch bzw. entspricht dann den Daten aus der Kompensations-
Rechnung. Über ZEMAX selbst lassen sich die erzielten Werte auf Plausibilität nochmals überprüfen.
Die Einzel-Linse führt ihn jedem Fall Achskoma ein, das man weitestgehend herausjustieren kann, vermutlich aber auch
Astigmatismus, entweder lagerungsbedingt, oder weil man nicht ganz auf der Achse mißt - ich habe es noch nicht ge-
nauer untersucht. Den Astigmatismus prüft man für gewöhnlich in RoC auf seine Größe.
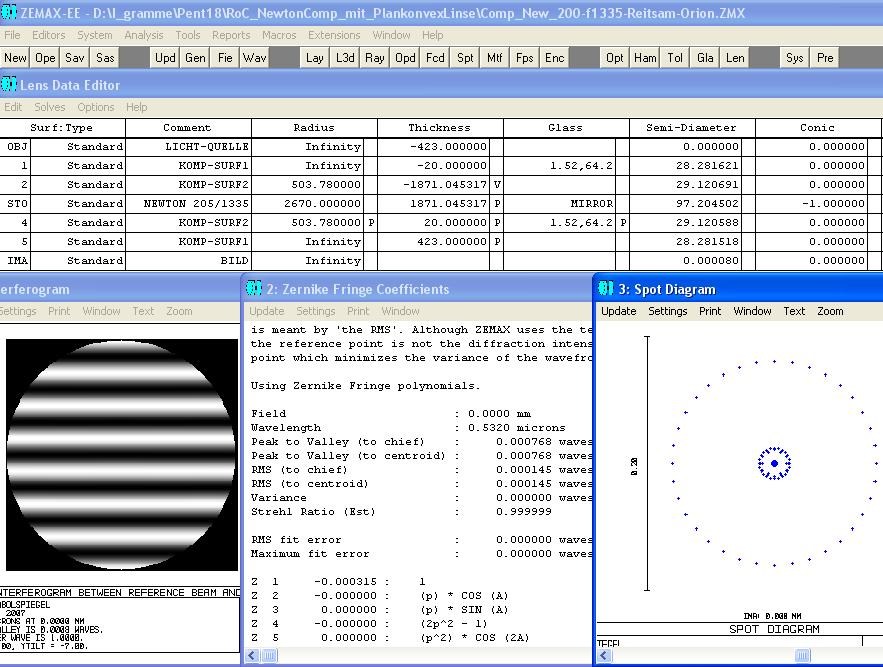
Auf einem 4 Meter langen Tisch stehen dann die Komponenten im richtigen Abstand hintereinander und sehr zu meiner
Zufriedenheit entstand sofort ein Interferogramm mit geraden parallelen Streifen, an dem man genau die Fehler erkennt,
wie sie bereits beim Zygo Certifikat erkennbar sind.

Hier eine Detail-Ansicht meiner 165 mm Durchmesser BK7 Plankonvex-Linse, 20 mm Mittendicke.

Das Kompensations-Interferogramm entspricht also sehr schön der Zygo-3-D-Darstellung. Lediglich ein leichter
Astigmatismus in Form ansteigender Streifenabstände stört den Frieden etwas. Gut erkennbar die Mulde in der
Mitte, die vom Fangspiegel verdeckt ist im späteren Teleskop und bei etwa 50% der oben erwähnte "Ring-Wall"
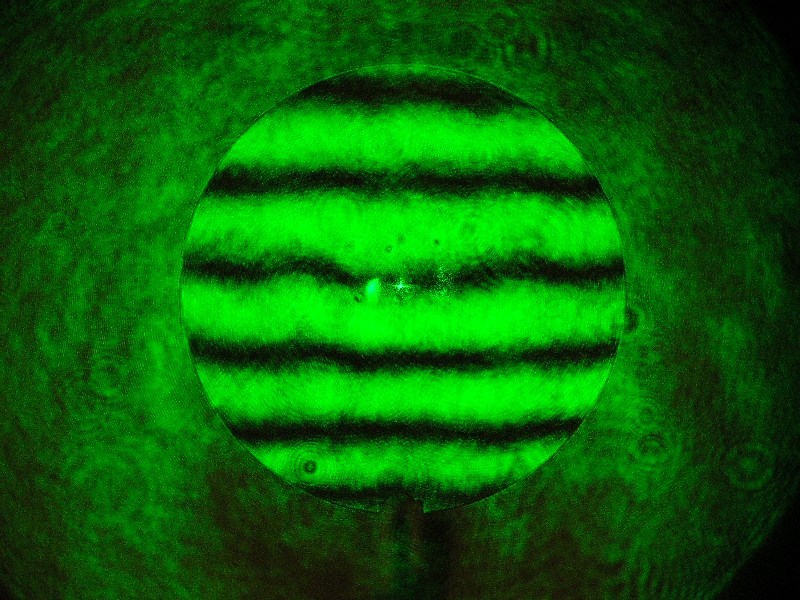
Hier die Auswertung des Kompensations-IGrammes
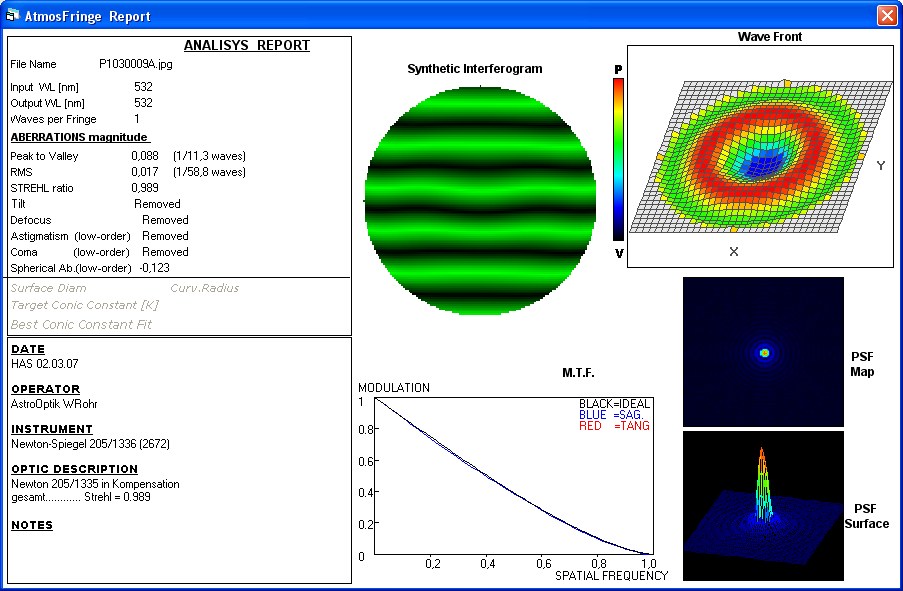
Das RoC-Interferogramm kommt ohne Kompensations-Linse aus, das Streifenbild muß allerdings auf Null zurückgerechnet
werden. Auch in diesem Fall kommt ein ähnlicher Wert heraus.

Zusätzlich der Test auf Astigmatismus, der die Frage beantwortet, ob oder wieviel Astigmatismus man bei der Wert-
Ermittlung abzieht.
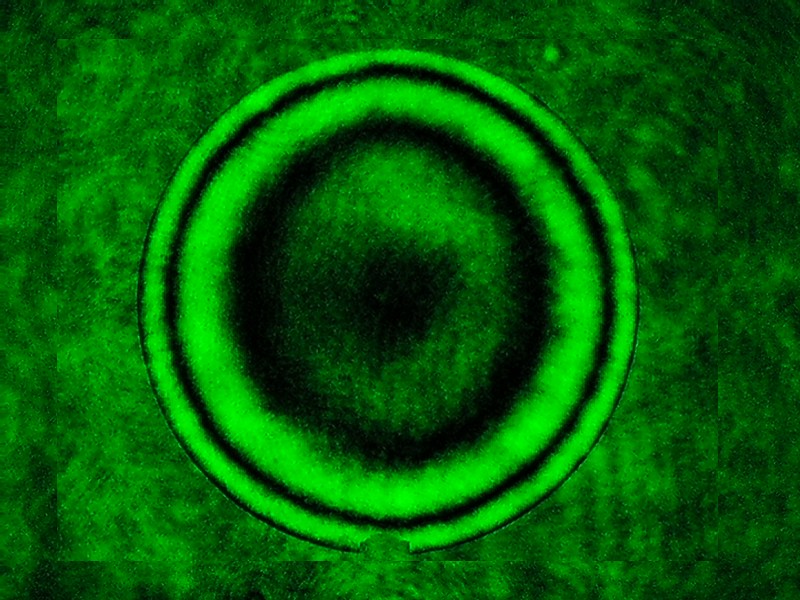
Auch auf dem auf Null zurückgerechnete Interferogramm ist die 3-D-Darstellung vom Zygo noch erkennbar, wegen der
Anzahl der Streifen nicht mehr so gut sichtbar.
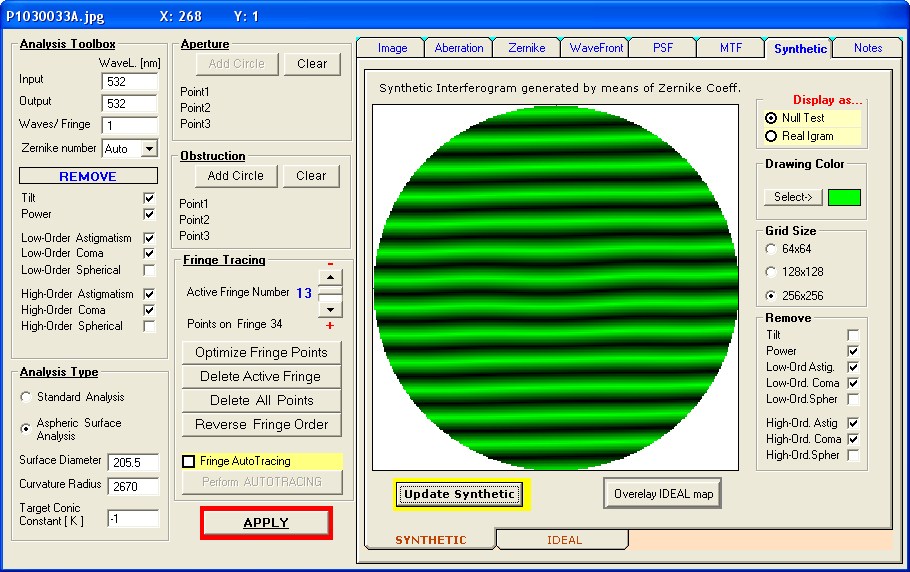

Wenn man einen engen Interferenz-Filter benutzt, dann lassen sich alle übrigen TEsts auch in Kompensation durchführen.
In diesem FAll der Ronchi-Gittertest und die Situation in der Mitte.

Auch beim Foucault-Test der gleiche Sachverhalt, wobei man darüber streiten kann, wie wesentlich die Differenz
zwischen der Transmissions-Kurve des benutzen Filters, und die von mir in der Zemax-Rechnung mit 532 nm wave
tatsächlich ist. Das Maximum der Filter-Kurve laut Diagramm läge bei 437 nm wave, ein Wert der sicher "spielt" ebenso
wie die Angabe bei den grünen DiodenLasern.

Ohne Interferenz-Filter, der grüne Sonnenfilter von Baader, hätte man keine Chance: Die Einzellinse hat ein breites
primäres Spektrum. Ein Achromat oder noch besser Apochromat wäre zwar besser, aber sündhaft teuer in der er-
forderlichen Qualität.

Auch ein Sterntest ist mit Interferenzfilter möglich, ohne Filter eine sehr bunte Angelegenheit. Der Sterntest zeigt
intra- wie extrafokal keine Auffälligkeiten, weshalb man von einem perfekten Spiegel ausgehen kann, der zudem
nach allen Regeln der Kunst von zwei Seiten geprüft worden ist.
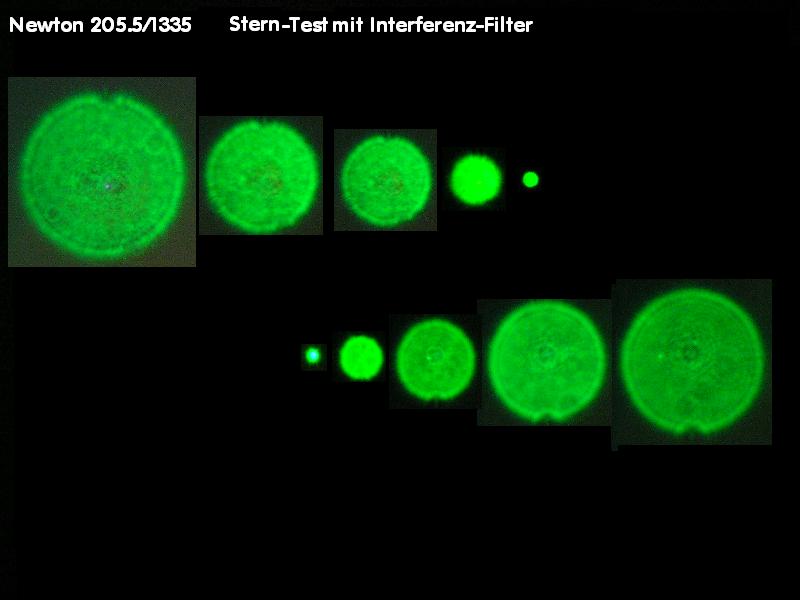
Es fehlen natürlich noch die Beweise aus der Praxis selbst. Aber der Sternfreund ist Mitglied unseres Forums, und das
läßt doch hoffen ...
E037 TOA 130-1000 Verkippung erzeugt Koma und Astigmatismus
Welcher Teleskop-Optik-Prüfer misst die MTF?
. . . und dazu die weiterführende Frage, wie läuft das in der Praxis ab, mit Fotos von Ergebnissen, deren Interpreation und Auswertungs-Verfahren.
Auffällig an solchen Erörterungen ist die Verabsolutierung einzelner Meßmethoden, bei denen offenbar nicht scharf abgegrenzt wird, für welchen Bereich sie sinnvolle Ergebnisse abliefern können: Auch der Strehl-Wert beantwortet viele Fragen nicht.
Interferogramme lassen sich auch im Feld einer Optik erzeugen. Das ist ein solches Beispiel. Es kommt etwas Altbekanntes heraus, daß nämlich ein Newton-Spiegel im Feld Koma hat. (Und weil das vermutlich ein Jeder weiß, ist die Frage eines Koma-Korrektors viel interessanter.) Danach kann man sowohl den Kipp-Winkel wie das Öffnungsverhältnis variieren und bekäme dazu passend immer den Strehlwert im Feld. Sehr viel informativer für diese Situation ist aber das Spotdiagramm (offenbar völlig in Vergessenheit geraten), besonders wenn man es mit dem Airy-Durchmesser vergleicht.
Wenn also für astronomische Optiken Certifikate auf ähnlicher Basis ausgestellt sind, u.a. von renommierten Herstellern, dann sollte man von einem Konsens ausgehen können, daß das so falsch nicht ist, was die certifizieren. Vor allem wäre zu differenzieren zwischen visuellen und fotografischen Ansprüchen. Im Übrigen das Grundthema dieses Threads.
Am Beispiel eines TOA 130/1000 Refraktors haben mich mal die Werte für Koma und Astigmatismus bei Felddurchmesser 20 mm interessiert:

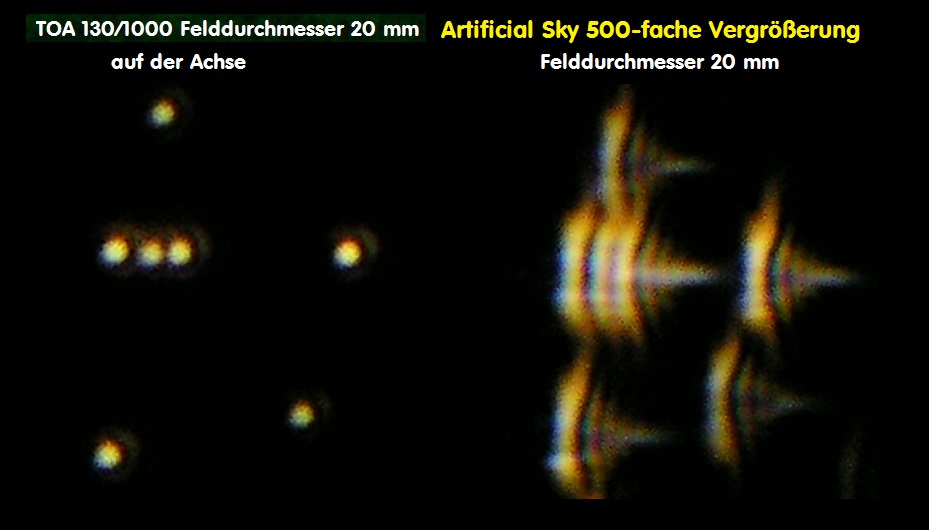

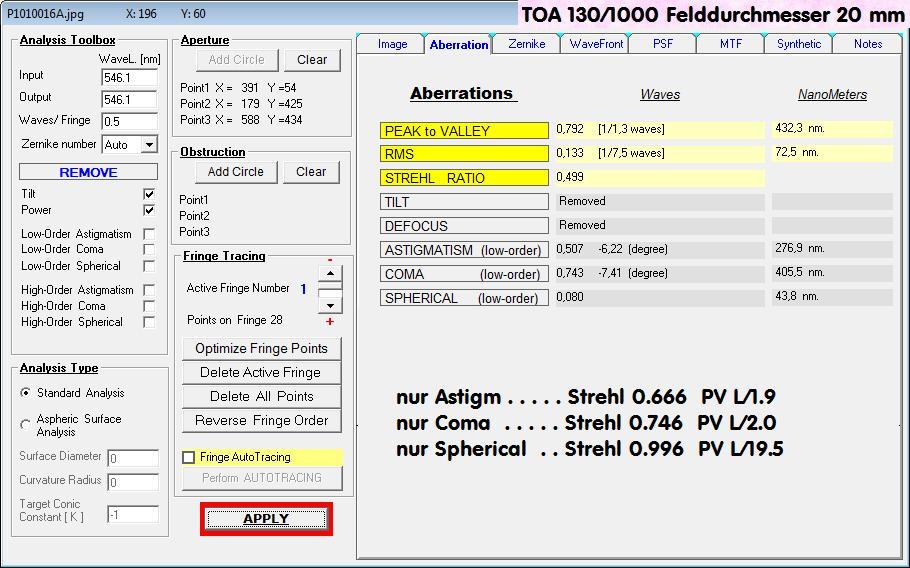

E036 APQ 110-840 Verkippung erzeugt Astigmatismus
Verkippung erzeugt Astigmatismus siehe auch TOA 130/1000 Verkippung erzeugt Koma+Astigmatismus
Dem Certificat eines betagten ZYGO fehlen alle wesentlichen Angaben, damit man es dem Objektiv zuordnen kann. Und damit ist dieses Certifikat
wertlos, obwohl mir glaubhaft versichert wurde, daß das folgende ZYGO-Certifikat als Qualitäts-Nachweis für einen APQ 110/840 präsentiert
worden war. Obwohl alle wesentlichen Daten auf dem "Papier" fehlen, stellt sich die Frage, warum ein APQ - auch noch aus einer Kleinserie für
eine Welt-Instituion - einen derart starken Astigmatismus haben sollte und noch m(i)ysteriöser ist der Umstand, daß wiederum der Astigmatismus
deaktiviert worden war, wofür es für dieses Objektiv keine Begründung gibt - es sei denn, dem Tester war bekannt, daß ein APQ im Feld deutlich
Astigmatismus zeigt, und er wußte, daß er dieses APQ nicht exakt vor dem Planspiegel kollimiert hatte. Für diesen Fall bliebe eine noch unerhebliche
Differenz, weil damit ein Restastigmatismus ganz verschwindet. Aber egal.
Das Computer-gezeichnete Interferogramm unten rechts im Bild zeigt also Astigmatismus in der Größe von PV L/2.6 bzw. Strehl = 0.882 und es besteht die berechtigte
Frage, ob bei einem in kleiner Serie für eine anspruchsvolle Anwendung dies überhaupt sein kann. Und wenn dies nicht der Fall sein kann, woher dann der Astigmatusmus
bei der ZYGO-Messung kommen kann. (Den Astigmatismus erkennt man entweder am konischen Auseinanderlaufen der Streifen, oder am ansteigenden Steifenabstand.)
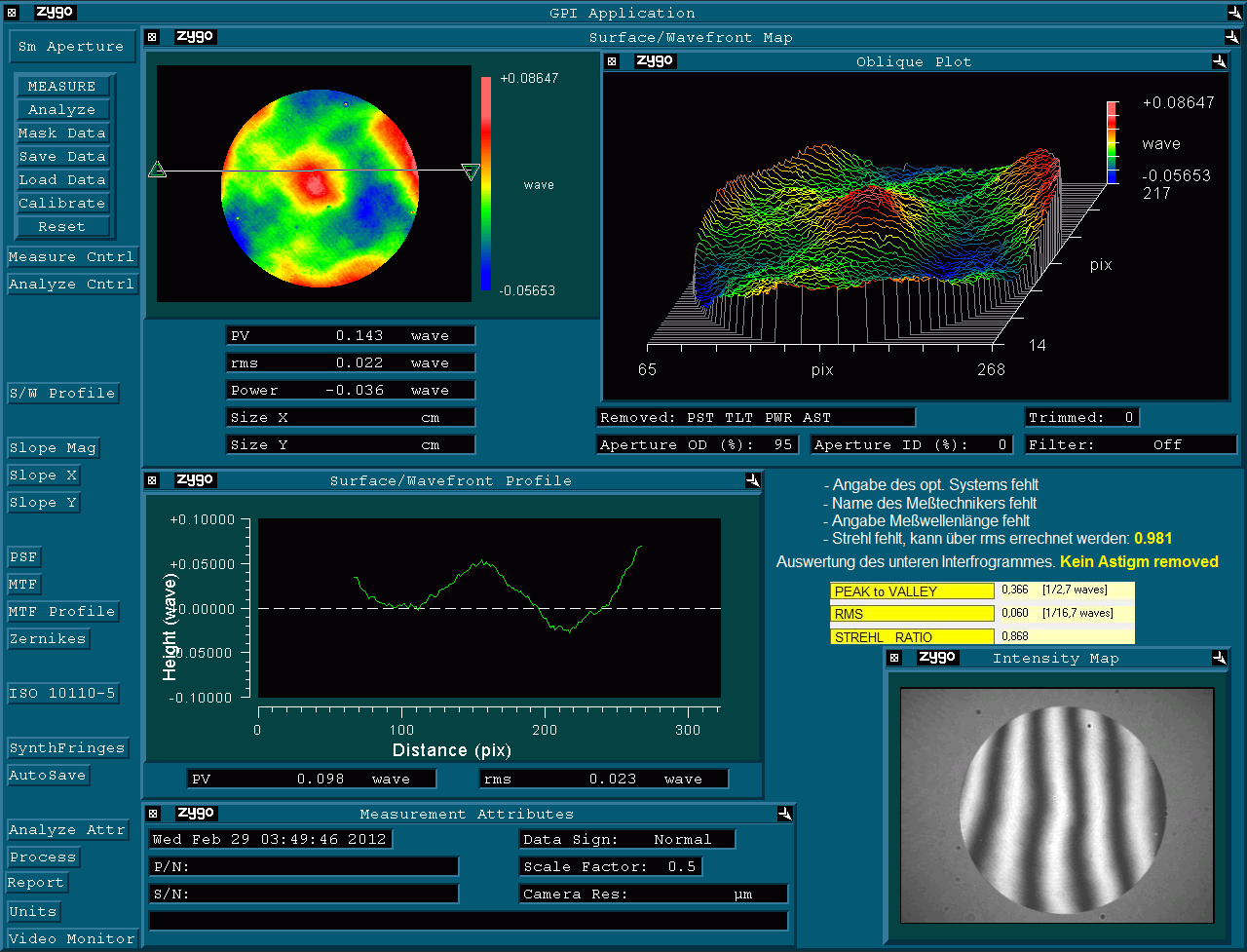
Das fragliche APQ aus einer Kleinserie

Und zunächst die Auswertung des computer-generierten IGrammes aus oberstem Certifikat.
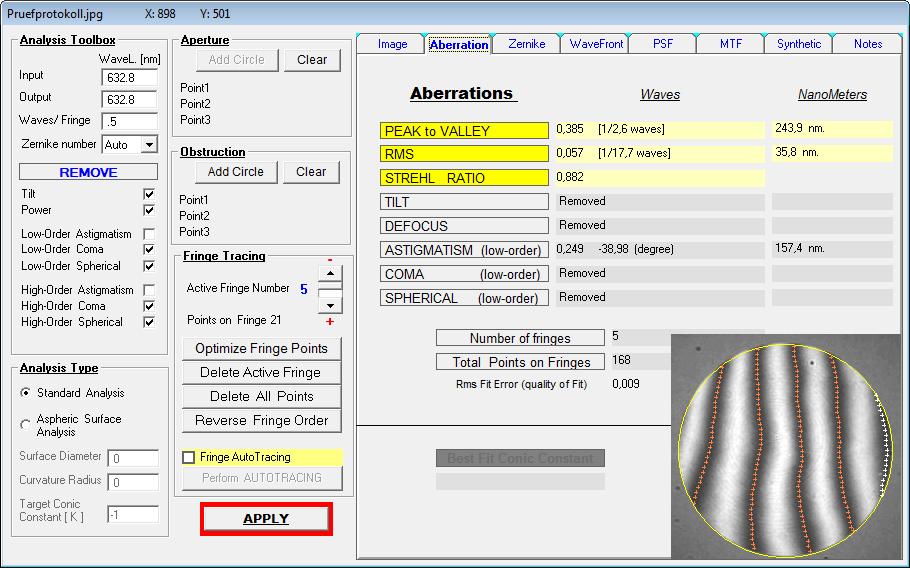
ontrollierte horizontale Verkippung
Anders als ein TOA, der beim gleichen Feldversuch eine Mischung aus Koma+Astigmatismus zeigte beim Igramm, reagiert der APQ bei
seitlicher Verkippung fast ausschließlich mit Astigmatismus, was sich über die ansteigenden Streifenabstände von oben nach unten
erkennen läßt. Dreht man zusätzlich die Streifen in Richtung der Vertikalen, dann werden die Bilder dem ZYGO-IGramm recht ähnlich.
Man kann sogar die Verkippung etwas eingrenzen, die beim ZYGO-Meßvorgang eine Rolle gespielt haben muß, also etwas mehr als
0.5° Verkippung.

Um also fälschlicherweise nicht eine Optik außerhalb der opt. Achse im Feld zu messen mit schlechteren Ergebnissen, ist mir die Notwendigkeit einer
exakten Zentrierung eines Objektivs vor dem Kollimations-Planspiegel bewußt. Nachfolgend eine kurze Anleitung, wie man ein Objektiv exakt zentriert.
Im 1. Schritt muß der 532 nm Laser-Pointer über den Planspiegel exakt in den Ursprung zurück-zentriert werden. Das ist gewissermaßen die
opt. Achse. Eine weiße Projektions-Fläche ist deshalb sehr hilfreich.

In diese "Testanordnung" wird nun im 2. Schritt das Ojektiv geschoben, das über die drei Raumachsen sowohl beweg-, wie verkippbar sein muß.
Diesen Vorgang kann man sehr deutlich an den Reflexbildern beobachten, indem man das Objektiv in Y, und Z bewegt und auch verkippt. Die opt.
Achse des APQ muß also mit dem Laserstrahl räumlich zusammenfallen. Das Ziel ist erreicht, wenn alle diese Reflexpunkte gemeinsam wieder im
Ursprung des Lasers verschwinden. Bereits bei diesem Vorgang lassen sich Zentrier-Fehler eines Objektivs erkennen. Für diesem Fall lassen sich die
Reflexbilder nicht auf einen Punkt zusammenführen.

Für die Feinbewegung haben sich folgende Bauteile bewährt:

E035B_Bericht Hotech Laser Collimator
Hotech Laser Collimator
Auf dem ITV 2013, "Vatertag der alten Säcke" wurde von Andreas Pietsch diese Zentriermöglichkeit für katadioptrische Teleskope vorgestellt, also
optische Systeme, die aus einem Haupt- und Sekundärspiegel bestehen und zusätzlich mit einer Schmidtplatte bzw. einer Meniskus-Linse bestückt
sind, wie es im untersten Bild auf der Internetseite dargestellt ist: http://www.hotechusa.com/category-s/23.htm
Wer also über keinen großen Planspiegel verfügt und ebenso keinen künstlichen Stern hat, den er in den Okular-Auszug stecken kann, der muß
entweder sein Schmidt-Cassegrain, Maksutov etc. am Himmel zentrieren (Polarstern), oder aber er legt sich dieses System zu, mit dem er ebenfalls
erfolgreich den Sekundär-Spiegel dieses Systems zentrieren kann: Dabei läßt aber bereits der YouTube-Film erkennen:
http://www.youtube.com/watch?v=ZNzBEqe5FlE , daß es sich in Wirklichkeit nur um die Zentrierung des Sekundärspiegels handelt. Der Hauptspiegel
müßte nach einem anderen Verfahren zentriert werden, was aber weniger oft der Fall ist. Auch für diese Art der Zentrierung ist ein wenig Übung
und opt. Fachwissen erforderlich. Siehe auch: http://www.youtube.com/watch?v=YanAqpo9ddQ&lr=1&uid=KYMiW3ew7ZdPLZ55wzGDeQ
Der Hotech Laser Collimator soll also in seiner Funktion dargestellt werden ohne die überflüssige Diskussion, wieviel besser andere Zentrier-Methoden sein mögen.
Je nach persönlicher Ausrüstung und Erfahrung gibt es mehrere Wege, Zit: "All CT, SCT, Makustov, & RC" zu zentrieren, wie es die Werbung im Link verspricht.
Warum ich allerdings die Einschränkung auf die Sekundär-Spiegel-Zentrierung mache, erkläre ich später.
Zunächst erscheint beim Auspacken eine "Schieß-Scheibe", in deren Zentrum ein Kreuz-Laser eingebaut ist und im vorletzten Ring auf 120° jeweils ein Punkt-Laser.
Über einen Schalter oben lassen sich diese verschiedenen Laser unterschiedlich einschalten.

Besser erklärt die Rückseite dieses Tablets (Bayerisch "Taferl") die Anordnung. Die Batterie unten muß mit dem Plus-Pol zum Betrachter eingelegt werden.
.

Eine wesentliche Einheit bildet dieser teildurchlässige kleine Planspiegel, der in die 2" Okular-Steckhülse eingesetzt wird und die drei Punkt-Laser im Fokus des
SC-Systems so zurückreflektiert wird, daß es im Ideal-Fall zum analogen Kreisring der "Schieß-Scheibe" wieder zu sehen ist, jeweils um 180° gedreht aus opt.
Gründen. Da dieser kleine Flat teildurchlässig verspiegelt ist, kann man von der Rückseite hinter dem Okularauszug den zentrischen Verlauf beim zusätzlichen
Einschalten der drei Punktlaser kontrollieren. Hier taucht aber zugleich das mechanische Problem auf, daß es immer ein Spiel zwischen Hülse und Spiegel-
Halterung von 0.1 - 0.2 mm gibt, sodaß das Festziehen der Hülsenschrauben bereits zu einer Verkippung dieses kleinen Spiegels führen kann, sodaß es besser ist,
diese Einheit lediglich einzulegen, aber nicht festzuschrauben bei horizontaler Test-Anordnung.
.

http://www.youtube.com/watch?v=ZNzBEqe5FlE Bereits die Anleitung auf YouTube zeigt, daß man das "Taferl" bzw. den HOTECH möglichst so aufstellt, daß der
Abstand zum Teleskop dort zu liegen hat, wo der Krümmungsmittelpunkt des Hauptspiegels liegt. Der Kreuzlaser wird dann als kleiner Kreis mit den vier Kreuz-
balken abgebildet, die man durch Verkippung zentrisch auf die Schießscheibe zentriert. Zuvor muß aber auch die Kreuzlaser-Figur zentrisch auf der Fangspiegel-
Einheit zu sehen sein, und später auch zentrisch auf der Rückseite der Hilfsspiegel-Einheit im Okular-Auszug.
.

Der "Prüfling" in Autokollimations-Anordnung: Zunächst wird nach einer Autokollimations-Testanordnung das C 9.25 vor einem 400 mm Planspiegel zentriert. Dazu braucht
man einen künstlichen Stern exakt auf der opt. Achse, wie man drei Bilder weiter sehen kann. Prinzipiell wird durch diesen Aufbau der Blick zum Himmel mit doppelter
Genauigkeit dargestellt. Diese Testanordnung zentriert sich in zwingender Weise selbst, weil man den künstlichen Stern erst sieht, wenn das System zum Kollimations-
Planspiegel exakt zentriert ist. Links im Bild also das C 9.25, rechts der Planspiegel.
.

Die gleiche Testanordnung mit einem 500-mm Zeiss Werkstatt-Planspiegel.
.

.
Die Einheit "künstlicher Stern" auf der opt. Achse, die in den Okular-Auszug gesteckt wird. Das Lichtleiter-Kabel leitet das Licht hinter die Pinhole aus Gründen
der Wärme, die die Lichtquelle erzeugt. Diese Wärme würde den Test-Vorgang empfindlich stören.

.
http://de.wikipedia.org/wiki/Sim%C3%A9on_Denis_Poisson Quote:
Poisson war ein Schüler von Pierre Simon Laplace und beschäftigte sich mit den physikalischen Grundlagen von Wellen, arbeitete über Akustik, Elastizität und Wärme sowie über die elektrischen Eigenschaften von festen Körpern. 1812 publiziert er eine Erweiterung der Laplace-Gleichung um die Oberflächenladung. 1818 sagte er den Poisson-Fleck voraus, wenn Licht Wellencharakter haben sollte. Dies bezweifelte er allerdings. Er führte heftige Diskussionen mit Christiaan Huygens als Verfechter der Wellentheorie des Lichts. Der Disput wurde durch den experimentellen Nachweis des Flecks durch François Arago beendet.[2] 1838 veröffentlichte er seine Wahrscheinlichkeitstheorie. Darin enthalten war die Herleitung der Poisson-Verteilung.
Die folgende Zentrierung am Stern benutzt den sog. Poisson-Punkt eines obstruierten Systems, was im 19.-Jahrhundert als Beweis für die Wellennatur des Lichts
angeführt worden war, siehe das Zitat aus Wikipedia. Dieser Punkt muß konzentrisch im defokussierten Sternscheibchen - bei hoher Vergrößerung - zu sehen sein.
Zuvor hatte ich also nach dieser Methode das C 9.25 zentriert und festgestellt, daß das C 9.25 sich in der Zwischenzeit offenbar etwas verstellt hatte: Der Poisson-
Punkt sitzt also nicht ganz zentrisch mittig in der "Figur", Bild links. Mit dem Bruchteil einer Drehbewegung an der analogen Zentrierschraube vorne an der Sekundär-
Spielgel-Einheit kann man das korrigieren.
Und hier die Begründung, warum "Bob Knobs" für diesen Fall sehr, sehr unpraktisch sind: An meinen Schrauben-Dreher ist ein Zeiger angebracht, damit ein Winkel-
Schritt von 1-3° noch erkennbar ist. Mehr ist für diese Korrektur oben gar nicht erforderlich. Unter hoher Vergrößerung bei ca. 1000-fach läßt sich das gut
kontrollieren.
.

Mit diesem perfekt zentrierten System sollte auch bei der HOTECH-Zentrier-Einheit ein gleiches Ergebnis herauskommen. In Beantwortung der weiter unten
folgenden Fragen nun der Verlauf der detaillierten Zentrierung:
Das Hotech-Tablet kann in den 3 Raumachsen verstellt und geneigt werden - eine ganz wichtige Voraussetzung bei der Einrichtung des gesamten Aufbaues
zusammen mit dem C 9.25, wie auf dem nächsten Bild zu sehen. Auch das C 9.25 kann ebenfalls - für alle Fälle - verstellt und geneigt werden.
01. Man schaltet also nur den mittigen Kreulaser ein und sucht zunächst den richtigen Abstand zum Hauptspiegels des C 9.25. Dieser zeigt sich dadurch, weil
das Reflex-Bild des Kreuzlasers, den der C 9.25 auf dem Hotech Tablet erzeugt in seiner Größe variiert, also bei richtigem Abstand auch nur als Punkt zu
sehen ist und kurz davor als Kreuzlaser mit Ring, der zu "Schieß-Scheibe" zentrisch sein sollte. Wenn dabei das Bild auf der C 9.25 Fangspiegel-Einheit sich
verschoben hat, so sieht man das auch auf dem Tablet als dezentrierten Reflex. Solange jedoch nur der Kreuzlaser eingeschaltet bleibt, wird man hinten im
Okular-Auszug nichts erkennen können, schon von der Logik her nicht, weil der Strahlengang des Kreuzlasers nur den Hauptspiegel erreicht, nicht jedoch das
ganze System. Das ändert sich erst, wenn man die 3 parallelen Punkt-Laser dazu-schaltet. Jetzt ergibt sich hinter dem kleinen teilverspiegelten Hilfs-Planspiegel
ein Fokus-Bild, abhängig davon, wo dieser Spiegel im Fokus steht.
02. Mit dem Kreuzlaser kann man genaugenommen nur den richtigen Abstand des Tablets zum C 9.25-Prüfling einstellen und in etwa die Höhe zur opt. Achse
beider Komponenten im Test-Aufbau. Man sollte sich unbedingt auch die oben angegebenen YouTube-Videos anschauen, damit man den Vorgang besser
nachvollziehen kann.
.

Erst nach dem Zuschalten der 3 Punkt-Laser, die prinzipiell ein paralleles Strahlen-Bündel aus dem Unendlichen darstellen, entsteht rückseitig im OAZ dieser Licht-
Fleck, der am Genauesten anzeigt, daß nun das System beiderseits zusammen auf der opt. Achse ist: Man wird also des öfteren die Komponenten feinzentrieren
müssen.
.

Entscheidend aber im 3. Vorgang ist die nächste Abbildung: Aus opt. Gründen entsteht wie bei jedem anderen Testaufbau ebenfalls ein seiten-verkehrtes auf dem
Kopf stehendes Bild, was mit den 3 Reflex-Punkten wahrgenommen wird. Einzige Bedingung: Diese Punkte müssen auf dem Kreisring liegen, auf dem auch die
Punkt-Laser ihren Ausgang genommen haben. Eine Verschiebung korrigiert man im YouTube-Film mit Hilfe der Bob Knobs.
.

.
Kritisch in diesem Zusammenhang ist, wie oben bereits erwähnt, das mechanische Spiel der Hotech-Okular-Spiegeleinheit mit dem 2" Okular-Auszug des C 9.25.
Innerhalb dieses Spiel kann man diese Laserpunkte "wandern" lassen. Es müßte deshalb eine Passung sein mit möglichst wenigen hundertstel Millimeter Spiel.
Bereits das Anziehen der Stellschrauben verändert die Lage der Punkte.

.
@ GSO RC 8-inch optisches Zentrierverfahren für Hauptspiegel sehr genau !
Neues GSO 8" f/8 RC - Ritchey-Cretién 203/1624___ Hauptspiegel-Zentrierung beim Cassegrain-System Abrollverfahren
@ GSO 8" RC - Hauptspiegel-Zentrierung über Laser-Beam Laser Pointer, für Andi 8-inch GSO RC Abrollverfahren
GSO 8" RC 203/1624 Auf die Spitze getrieben Hauptspiegel Restastigmatismus eliminieren
.
Wie man aus den Links ersehen kann, muß bei manchen Systemen auch der Hauptspiegel zentriert werden. Bei einem RC-System (GSO-RC) würde ein
dezentrierter Hauptspiegel Astigmatismus erzeugen. (Eine andere Ursache für Astigmatismus im System wäre die Hauptspiegel-Lagerung selbst: Bei
manchen SC-Systemen und Maksutovs.) Die unterschiedlichen Möglichkeiten der Hauptspiegel-Zentrierung ist in den oberen Links dargestellt, entweder
als Abroll-Verfahren, oder im Krümmungsmittelpunkt des Hauptspiegels im Zusammenhang mit der opt. Achse. Auch über die Astigmatismus-Figur
könnte man den Astigmatismus des Hauptspiegels bei Dezentrierung desselben eliminieren. Prinzipiell läßt sich der Hotech Laser Collimator für die
Fangspiegel-Zentrierung verwenden. Die Anschaffung dieser Einheit entspricht in etwa einem hochwertigen Ethos-Okular.
Nachtrag:
Ein paar erklärende Zeichnungen aus dem YouTube-Film:
Der Cross Hair / Kreuz-Laser wird nur zu Zentrierung des Test-Aufbaus benutzt. Sein Licht erreicht wegen der Obstruktion des Sekundär-Spiegels den Hauptspiegel nicht.
In diesem Fall sieht man im Okularauszug keinerlei Licht-Reflex.
Der Hauptspiegel reflektiert nur den Kreuzlaser auf die "Schieß-Scheibe" zurück, abhängig vom Abstand, den diese vom Hauptspiegel selbst hat. Vorteilhaft ist
in der Nähe des Krümmungsmittelpunktes vom Hauptspiegel.
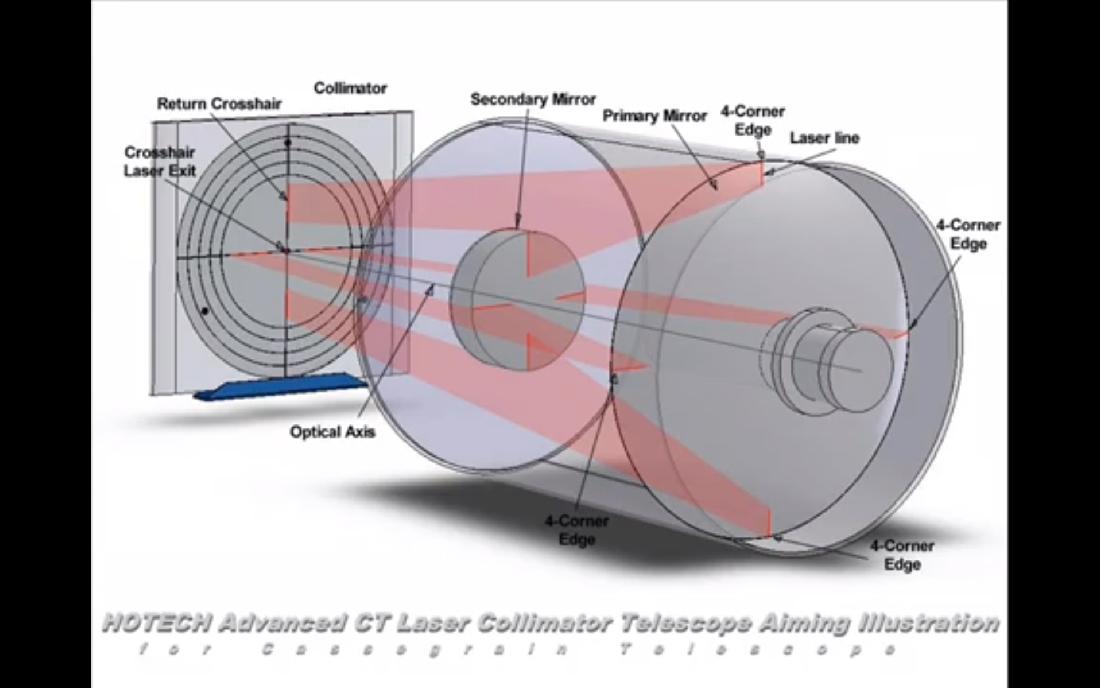
Erst wenn man die drei äußeren parallelen Punkt-Laser dazuschaltet, die das parallele Strahlen-Bündel simlieren sollen, durchlaufen dieses stellvertretend für
ein Bündel mit dem vollen Durchmesser das opt. System bis zum Planspiegel im Okular-Auszug und werden dort reflektiert und auf die "Schieß-Scheibe"
zurück-reflektiert, je nach Justier-Zustand des Systems. Eine Kontrolle, ob der kleine Planspiegel wirklich eine Total-Reflexion auf der opt. Achse ermöglicht,
gibt es leider nicht, weil die Okular-Auszug-Hülse dafür zu viel Spiel hat. Hier hilft nur der Sterntest am großen Planspiegel weiter, mit dem man auch einen
möglichen Astigmatismus erkennen kann.
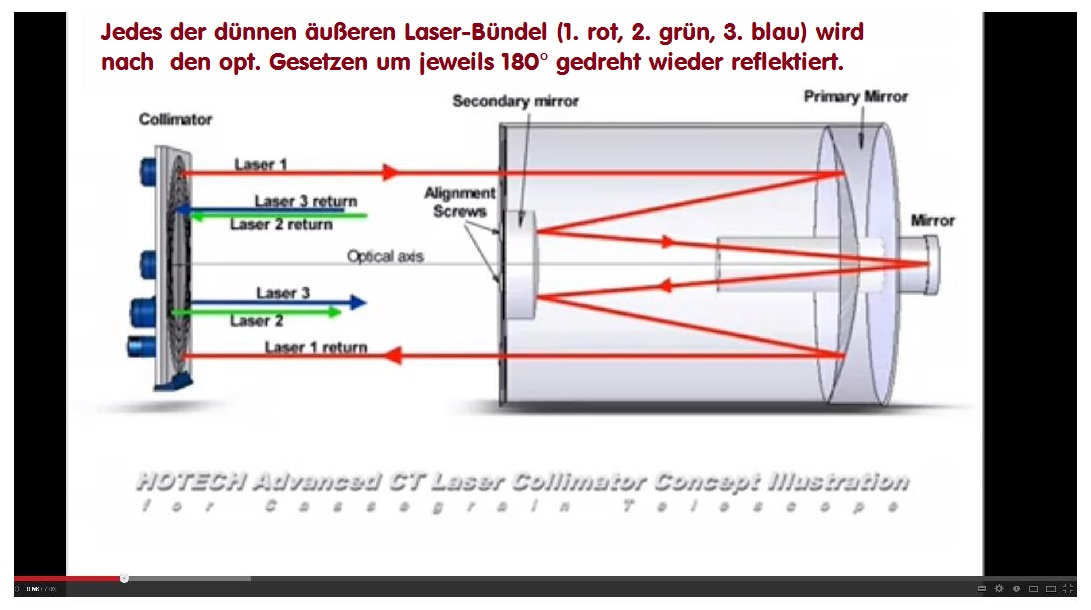
Beantwortung der Frage in Beitrag #11 von Volker:
Überprüfung der Kollimation von HOTECH Laser Collimator
Wer der Technik dieses HOTECH Laser Collimator mißtraut, hat eine einfache Möglichkeit, dies zu überprüfen:
Im Abstand von 1.5 - 2.0 Meter stellt man die Komponenten zueinander orientiert auf. Links der HOTECH Laser Collimator, rechts ein 20 cm Zeiss Planspiegel.
.

.
Im eingeschalteten Modus schickt der HOTECH Laser Collimator (HLC) vier Bündel zum Flat: mittig den Kreuzlaser und außen je einen Punktlaser, die alle
zueinander räumlich pparallel sein müssen. Der besseren Sichtbarkeit wegen zunächst die Projektion auf eine weiße Fläche.

Jetzt auf dem Flat zu sehen, der aber die vier Bündel in sich total-reflektiert und zum HLC zurückschickt.
.

.
und wie erwartet, landen alle Bündel wieder dort, wo sie eigentlich landen müssen: Das Laser-Kreuz auf dem Kreuz der "Schieß-Scheibe", die drei Punktlaser dort,
wo sie hergekommen sind. Der Kollimator ist technisch also in Ordnung.

.
.
E032 Howie Glatters Laser Collimator - eigener BerichtE032 Howie Glatters Laser Collimator - eigener Bericht

Howie Glatters Laser Collimator
In meinem Bereich ist dieses "Tool" ein sehr wertvolles Hilfsmittel. Beim Wiedereinbau des Sekundärspiegels in ein Dall-Kirkham-System liefert das
Autokollimations-Setup erst dann ein Ergebnis, wenn der Sekundärspiegel das Lichtbündel wenigstens durch das Blendrohr zurückwirft. Man könnte
natürlich auch okularseitig auf den Sekundärspiegel blicken und solange den Spiegel verkippen, bis man das eigene Auge wieder sehen kann. In beiden
Fällen ist aber das System noch nicht zentriert und erst wenn keine Koma mehr zu erkennen ist, wäre die Zentrierung perfekt.
Der Laser-Collimator hat austauschbare Einsätze (weiße Scheibe) die konzentrische Kreise, Gitter oder konzentrische Interferenz-Ringe zeigen und
für die Zentrierung sehr hilfreich sind.

Leider ist das Spiel von bis zu 0.15 mm bei den Okular-Auszügen ein Hinternis, eine Kollimation exakt durchzuführen. Man wird die Zentrierung
optisch vor einem Planspiegel nachbessern müssen. Trotzdem beschleunigt dieser Collimator den Zentriervorgang enorm.

In diesem Beispiel erzeugt der Kollimator konzentrische Beugungs- oder Interferenz-Bilder.

Howie Glatter Laser Collimator, Kollimation, Zentrierung Zweispiegel System, Align , http://www.collimator.com/coltext.htm
Howie Glatter Laser Collimators , Howie Glatter TuBLUG 2" Newtonian Laser Collimator , Great Red Spot Astronomy Products ,
E031 ZweispiegelSystem Zentrierung PrimärSpiegel auf opt Achse
Zentrierung des Primär-Spiegels auf der opt. Achse
Zweispiegel-Systeme oder aber nur dessen Primär-Spiegel, lassen sich auf folgende Arten zentrieren. Für fotografische Benutzung sollte dieses Verfahren
ausreichend sein. Das Bild zeigt den Primär-Spiegel eines Cassegrain-Systems mit einem Krümmungsradius (RoC) von ca. 2000 mm. Der Hauptspiegel hat
notwendigerweise eine Bohrung, durch die man später durchschaut von der Rückseite dieses Spiegels. Man kann nun entweder in diese Bohrung selbst
einen Laser-Pointer einsetzen, der dann - justierbar - auf den Punkt in RoC gerichtet werden muß, oder aber man startet über dem Krümmungsmittel-
punkt (RoC) das Verfahren, wie die folgenden Bilder zeigen.
Der Spiegel und seine Lagerung müssen verkippbar sein - deshalb die untere Stellschraube für die Höhe - verdrehbar ist diese Lagerung ohnehin.

Auf seiten der Lichtquelle sieht man nun den Laser-Pointer in seiner eindeutigen Lagerung: Die vordere Schraube ( Nr. 1) hält ihn in der Buchse fest, mit der hinteren
gerändelten Schraube ( Nr. 2 ) kann man ihn ein- und ausschalten. Links daneben erkennt man das 5 mm Okular, das mit einer Halterung versehen ist, damit man es
auf den Laser-Pointer im zweiten Schritt aufstecken kann. Das Ganze ist auf einer Hub-Bühne aufgesetzt, damit man auch dort die Höhe fein verstellen kann.

Nun schaltet man den Laser ein, und richtet ihn auf das Zentrum des vorher gezeigten Primär-Spiegels.

Das erkennt man auf der Spiegelseite: Der Laser-Pointer trifft durch die Bohrung des Hauptspiegels die Rückseite meiner Holz-Lagerung.

Nach der Ausrichtung des Laser-Parallel-Bündels a) zum Hauptspiegel und b) zurück zum Laser-Pointer selbst, steckt man nun das 5 mm Okular auf den Laser
und erzeugt aus dem Parallel-Bündel einen Lichtkegel. Weil die Laser-Lichtquelle ziemlich genau im Krümmungsmittelpunkt ( 2 000 mm ) des Primär-Spiegel ist,
entsteht so über das divergente Bündel - vom Okular erzeugt, der Reflex vom Hauptspiegel. Der Sichtbarkeit wegen ein bißchen nach hinten verschoben.
Wenn beide Bündel konzentrisch zusammenfallen, dann stellt das Parallel-Bündel des Laser-Pointers die opt. Achse des Primär- oder Hauptspiegels dar. Damit
läßt sich bereits überprüfen, ob bei einem fotografischen System der Hauptspiegel exakt zur Fokus-Ebene ausgerichtet ist.

Eine andere Möglichkeit bietet eine helle Pinhol mit Durchmesser 1 mm. Die Lichtquelle bildet ein Auto-Scheinwerfer-Birnchen in dem Alu-Rechteckrohr, in das die
1mm Pinhole gebohrt worden ist. Außerhalb erkennt man die weiße ProjektionsFläche.

Auch hier stellt man diese Lichtquelle in den Krümmungsmittelpunkt und justiert Spiegel und Lichtquelle so, daß man den Reflex-Punkt auf diese Projektionfläche
bekommt.

Die Situation noch etwas vergrößert . . .

und nun ebenfalls leicht versetzt neben der Pinhole die Reflex-Scheibe des Primär-Spiegels im Krümmungsmittelpunkt. Auch damit läßt sich die opt. Achse darstellen,
die gebildet wird über die Mitte der Primärspiegel-Bohrung und der Mitte der 1 mm Pinhole. Je nach Erfordernis läßt sich dieser Testaufbau variieren.
Der erste Bericht oben zeigt bereits einige weitere Möglichkeiten.

E030 Aligning a Cassegrain System in front of a Flat Cassegrain- Zentrierung- Setup
Aligning a Cassegrain System in front of a Flat
cross laser module: Picotronic

Quote:
Preface
A two mirror system e.g. SC, Cassegrain or RC has a definite distance of the two mirrors, a definite focus plane and both mirrors are
exact on optical axis. There are some ways to bring them there. After this, you can add a collimation flat behind the secondary or
behind the two-mirrors-system for total reflecting the outcoming parallel beam of that system. This would be the testing setup for this.
A) You can start with the main mirror (primary). In the hole of the primary you insert a laser module, laser pointer or aligned laser system. This should
be exact vertical to the mirrors surface. You can realise it by a bearing bush with a ring what touches the mirrors surface and runs with optical axis.
With a aligned laser system, as this foto shows, you can produce this bearing bush via a lathe with synthetic material, as the foto shows. Note the red
arrows, this would be the contact ring. In a second step, you align the secondary what is fixed at a normal spider. Now the two mirrors system will
be aligned back with the laser. At last you remove the laser from the primary and align the collimation flat to this system with a divergent bright light
source at the focus. At the focus you can test this system in different ways. With Ronchi, Foucault or interferometer.
A1) The laser beam or the cross laser at the primary mirror you also can align, if you insert at the radius of curvatury a bright divergent pinhole beam.
Note this: http://rohr.aiax.de/CassZ_20.jpgThis would be the mirrors center, and the center of any laser module have to point there. Note that foto.
B) To avoid a spider for the secondary and if your flat has a hole, there you can insert the secondary, as the following report shows. Now you also
need the primary mirror with it's concentric laser beam. For the collimation flat, there you need a small flat, that surface has to coninside with the
surface of the big flat, as this foto shows. (kleiner Planspiegel) This you can realise with a bearing bush, too. Note the foto.
Later you remove the small flat and insert the secondary, and then you align this one back to the primary mirror without moving the collimation flat.
C) You also can use a cross laser module. You also start with it at the primary and there it has to run with the optical axis. This condition is very
important. You can put a bright pinhole at mirrors radius of curvature, and there have to point the center of the cross laser modul. Then you
align the big flat mirror with the cross laser and at last you insert the secondary, as my report shows later. Note that foto.
.
Neues GSO 8" f/8 RC - Ritchey-Crétien 203/1624 ___ Hauptspiegel-Zentrierung beim Cassegrain-System Abrollverfahren
GSO 8" RC - Hauptspiegel-Zentrierung über Laser-Beam Laser Pointer, 8-inch GSO RC Abrollverfahren

This was a report to check a Cassegrain-System in front of a flat. Both mirrors were aluminized. For this it's easier to align this setup.
In principle this should work with uncoated mirrors, too. The mirrors distance define the fokus plane, this is one of the problem. The
other one is the tipping of one of the components and at last, how bright the light source are. The best one for that would be a bright
laser module with an addional eyepiece, or any cross laser module. With this setup you will arrange different tests: Ronchi, Foucault,
interferogramms.
This was a report in 2010 with this problem, aligning a Cassegrain System in front of a Flat. The main mirror shows a lot of astigmatism, and so
you should test at first the optical quality of it. The flat I used has a drilled hole of 80 mm. There you can insert the secondary mirror and
align this one from the back as the foto shows at right.
http://www.astro-foren.de/showthread.php?p=49892#post49892
http://www.astro-foren.de/showthread.php?t=12248
Main mirror left - Secondary in the middle and the aligning system for Secondary in the back of the flat

http://rohr.aiax.de/CassZ_20.jpg
This shows the setup of a Cassegrain-system. It's better to use a flat with a drilled hole, so you can insert there the secondary and align it there on the back.
Without a hole you have more problems for a setup.
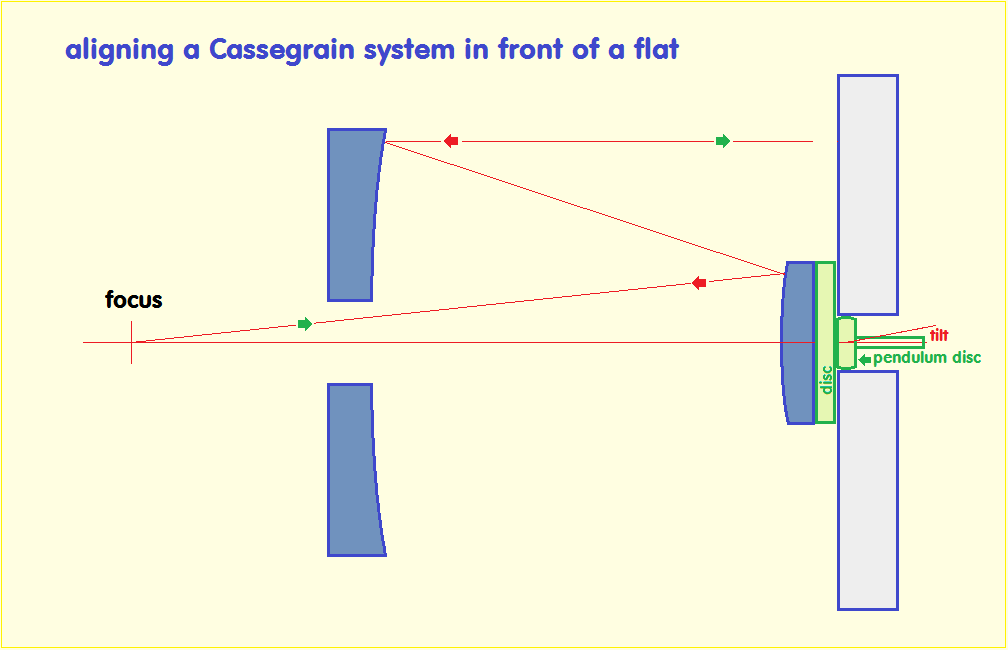
I use a flat with 400 mm diameter and 80 mm hole. In this hole I insert different tools: A small flat mirror, to bring the large flat mirror on optical axis.
Some tools to fix a Cassegrain secondary on the "Haltescheibe", a small 1 1/4 inch disc for tilting the secondary with a longer thread rod on the flats back
as it shown on the first foto with "Kunststoff-Zylinder". Normally I insert a laser pointer for aligning a Newton mirror for an autocollimation test.

This shows the wooden disc what fixes the secondary with the same diameter. A thread rod is bonding the pendulum disc from plastic. This is
inserted in the plastic bearing bush with a tool for aligning this unit.

This is the flat with 400 diameter and a 80 mm hole.

This shows, how you can align a laser modul at the primaries hole:
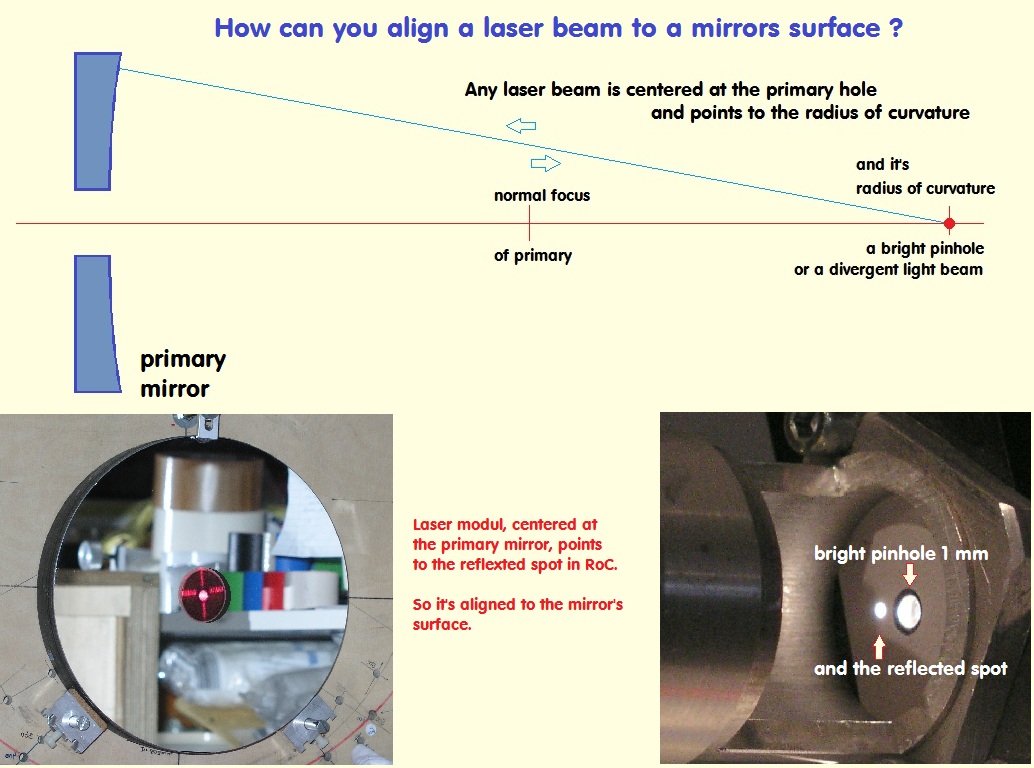

Now some cross laser modules

And this shows, how they work


But there is a third possibiliy for aligning this set up:
01. With the normal laser pointer, you align at first the secondary on optical axis. (The mirrors distance must be correct.)
02. Then you add the eyepiece on the laser and so you get a divergent light beam. With this, it should be possible, to align the main mirror and at last
03. the flat

A bright light source with 1 mm diameter and a car light bulb could be another option.

This is the wooden box what keeps the primary mirror, it has a hole and the box, too: http://www.astro-foren.de/showthread.php?t=12248

This are the plastic cylinders what keeps the laser module. They are made for different diameters. For every primary I have to produce a new one !

Note the arrows! This is running with the mirrors surface.

And this is the flat with the secondary mirror.

##################################################################################
Zentrierung des Primär-Spiegels auf der opt. Achse
Zweispiegel-Systeme oder aber nur dessen Primär-Spiegel, lassen sich auf folgende Arten zentrieren. Für fotografische Benutzung sollte dieses Verfahren
ausreichend sein. Das Bild zeigt den Primär-Spiegel eines Cassegrain-Systems mit einem Krümmungsradius (RoC) von ca. 2000 mm. Der Hauptspiegel hat
notwendigerweise eine Bohrung, durch die man später durchschaut von der Rückseite dieses Spiegels. Man kann nun entweder in diese Bohrung selbst
einen Laser-Pointer einsetzen, der dann - justierbar - auf den Punkt in RoC gerichtet werden muß, oder aber man startet über dem Krümmungsmittel-
punkt (RoC) das Verfahren, wie die folgenden Bilder zeigen.
Der Spiegel und seine Lagerung müssen verkippbar sein - deshalb die untere Stellschraube für die Höhe - verdrehbar ist diese Lagerung ohnehin.

Auf seiten der Lichtquelle sieht man nun den Laser-Pointer in seiner eindeutigen Lagerung: Die vordere Schraube ( Nr. 1) hält ihn in der Buchse fest, mit der hinteren
gerändelten Schraube ( Nr. 2 ) kann man ihn ein- und ausschalten. Links daneben erkennt man das 5 mm Okular, das mit einer Halterung versehen ist, damit man es
auf den Laser-Pointer im zweiten Schritt aufstecken kann. Das Ganze ist auf einer Hub-Bühne aufgesetzt, damit man auch dort die Höhe fein verstellen kann.

Nun schaltet man den Laser ein, und richtet ihn auf das Zentrum des vorher gezeigten Primär-Spiegels.

Das erkennt man auf der Spiegelseite: Der Laser-Pointer trifft durch die Bohrung des Hauptspiegels die Rückseite meiner Holz-Lagerung.

Nach der Ausrichtung des Laser-Parallel-Bündels a) zum Hauptspiegel und b) zurück zum Laser-Pointer selbst, steckt man nun das 5 mm Okular auf den Laser
und erzeugt aus dem Parallel-Bündel einen Lichtkegel. Weil die Laser-Lichtquelle ziemlich genau im Krümmungsmittelpunkt ( 2 000 mm ) des Primär-Spiegel ist,
entsteht so über das divergente Bündel - vom Okular erzeugt, der Reflex vom Hauptspiegel. Der Sichtbarkeit wegen ein bißchen nach hinten verschoben.
Wenn beide Bündel konzentrisch zusammenfallen, dann stellt das Parallel-Bündel des Laser-Pointers die opt. Achse des Primär- oder Hauptspiegels dar. Damit
läßt sich bereits überprüfen, ob bei einem fotografischen System der Hauptspiegel exakt zur Fokus-Ebene ausgerichtet ist.

Eine andere Möglichkeit bietet eine helle Pinhol mit Durchmesser 1 mm. Die Lichtquelle bildet ein Auto-Scheinwerfer-Birnchen in dem Alu-Rechteckrohr, in das die
1mm Pinhole gebohrt worden ist. Außerhalb erkennt man die weiße ProjektionsFläche.

Auch hier stellt man diese Lichtquelle in den Krümmungsmittelpunkt und justiert Spiegel und Lichtquelle so, daß man den Reflex-Punkt auf diese Projektionfläche
bekommt.

Die Situation noch etwas vergrößert . . .

und nun ebenfalls leicht versetzt neben der Pinhole die Reflex-Scheibe des Primär-Spiegels im Krümmungsmittelpunkt. Auch damit läßt sich die opt. Achse darstellen,
die gebildet wird über die Mitte der Primärspiegel-Bohrung und der Mitte der 1 mm Pinhole. Je nach Erfordernis läßt sich dieser Testaufbau variieren.
Der erste Bericht oben zeigt bereits einige weitere Möglichkeiten.

E028 Stoffies Interferometer Zentrieren-Kollimieren
Ein Interferometer entsteht.
Für unser Foren-Mitglied Ronny sollte ich schon seit längerem einen Bath-Interferometer herstellen. Und weil er seinen Spiegel bereits poliert, was es höchste Zeit, das Prüfgerät fertig zu stellen. Dazu sind aber sowohl einige Teile zu besorgen oder in einer Drehmaschine bzw. Fräsmaschine vorzubereiten.
Optische Komponenten:
Laserdiode, 3 mW, Durchmesser 11.3 mm, 4.5 Volt, Conrad Elektronics
Teilerwürfel 17.8 mm Kantenlänge, Teilerfläche 50% / 50%, nicht polarisiert, normale Qualität
Bikonvex Einzel-Linse, 10 mm Brennweite, Durchmesser 5,5 mm, SurPlus
Prisma mit verspiegelter Hypothenuse, 16 mm hoch, Quelle unbekannt
Nach diesen Abmessungen richtet sich nun der Aufbau der Anlage:
Die Optische Achse liegt in der Mitte des Teilerwürfels, und damit 18/2 = 9 mm über der "Basis"-Fläche eines 40x40 mm Alu-Rechteck-Rohres mit 2 mm Wand und dunkler Beschichtung. Zwischen der Lichtquelle, und dem eigentlichen Interferometer-Aufbau läßt man für Filter bzw. Strahlaufweitungs-Optik etwas Spielraum, das man nachträglich dort einfügen kann bei Bedarf. Da das Laserbündel ca. 2 mm im Durchmesser ist, entsteht über die 5.5 mm Linse ein Lichtkegel von nur f/5 und das begrenzt die Verwendung dieses Interferometers auf f/5 und kleiner. Erst bei voller Ausleuchtung des 5 mm Linsen-Durchmessers entsteht ein genügend großer f/2 Lichtkegel, was beim Prüfen von f/4 Öffnungen ganz wichtig ist. F/4 Newton-Spiegel in Autokollimation geprüft wären so ein Fall.
Mechanischer Aufbau
Dieses ca. 200 mm lange 40x40 mm im Querschnitt große Alu-Rechteck-Rohr bekommt nun ganz links je einen Schlitz, damit man später die Laserdiode mit Halter justieren kann, wie nachfolgende Bilder zeigen. Daran schließt sich ein Befestigungs-Schlitz an, der nach oben offen ist, damit man den Halter von oben einschieben kann. Im rechten Bereich erkennt man die M4-Gewinde für die Halteschrauben eine Stahlplättchen von 0.4 mm Dicke, (Abreißlineal für Tapeten), auf dem der spätere Teilerwürfel aufgesetzt und vor allem justiert werden kann. Ganz rechts wieder ein Befestigungs-Schlitz für den Halter der Bikonvex-Linse, der ebenfalls eingeschoben wird.
Der Halter der Laserdiode wurde aus einer 30 mm gezogenen Alu-Stange (Dreh- und Bohrqualität) hergestellt, ca. 30 mm lang.. Die Laserdiode steckt am rechten Ende, wo das Licht-Bündel austritt so in einer paßgenauen Bohrung von 11.3 mm und 2mm Tiefe. Nach hinten zu, also links wird mit einer Bohrung von ca. 15 mm genügend Spiel zur Justage der Laserdiode erzielt. Die Justage-Madenschrauben M4 sind im Winkel von 120 Grad angeordnet. Der Durchmesser des Halters wurde auf 24.3 mm plan abgefräst, wobei gleichzeitig noch die Dicke des Teilerwürfel-Plättchens mit eingerechnet wurde. Mit diesem Maß wird die Höhe des Laserbündels von 9 mm über Grund eingehalten. Erfreulicherweise entstanden alle Teile mit einer Genauigkeit von 0.1 mm.


Zunächst paßt man das 0.4 mm Federstahl-Plättchen auf die Position des Teilerwürfels und der Basis an, versieht es mit zwei Langlöchern für M4 Inbus-Schrauben und schraubt das Plättchen mittig fest, damit man es später in beide Richtungen verschieben kann und noch leicht drehen kann. Nach dem gleichen Prinzip funktioniert die Befestigung des Halters der Laserdiode. Nun hat man zwei Dinge zu prüfen: Ist das Laser-Bündel parallel zur Basis, was man daran untersucht, ob das Bündel mittig durch die Linse im Linsenhalter fällt. Das justiert man an den drei Justierschrauben Laserseitig. Die nächste Prüfung geht dahin, festzustellen, in welcher Position der Teilerwürfel sowie die Laserdiode stehen müssen, damit aus dem Teilerwürfel zwei Lichtbündel im Abstand von ca. 5-10 mm austreten und an einer ca. 4 m entfernten Wand möglichst dicht nebeneinander zu sehen sind. Dabei ist von besonderer Wichtigkeit, daß das vom Laser kommende Ursprungs-Bündel oberhalb der Teilerfläche in den Würfel eintritt. Sonst entstünde ein spiegelverkehrter Aufbau, der natürlich ebenso möglich wäre. Auch in Verbindung mit einer Bikonkav-Linse würde das System funktionieren. Unter den gerade beschriebenen Bedingungen markiert man nun die Orientierung des Teilerwürfels auch auf der Unterlage des Stahlplättchens mit einem dünnen Folienstift. In dieser Position und Orientierung wird nun über ein Doppelklebe-Textil-Band aus dem Teppichhandel der Würfel schonend auf der Unterlage befestigt. (Aus diesem Grund sollte man den Bath-Interferometer nie waagrecht lagern, weil sich sonst der Würfel verschiebt und ablöst.

Besonderes Augenmerk liegt nochmals auf dem Halter der kleinen Bikonvexlinse mit einem Durchmesser von 5,5 mm und einer Randdicke von 1.2 mm, dünner ist besser als zu dick. Dieser Linsen-Halter ist aus dem gleichen 30 mm Alu-Stangen-Material hergestellt mit einer Dicke von ca. 8 mm. Die Linse sitzt in einer Bohrung von 5.6 mm und wird vorne gestoppt durch einen Ansatz von nur 5 mm. Von unten ist diese Alu-Scheibe wieder auf die 24.3 mm abgefräst, um die Höhe der opt. Achse einzuhalten und zum Betrachter zu wird soviel Material rechtwinklig abgefräst, daß der LinsenRand bündig zur abgefrästen Fläche ist, damit beide Bündel ungehindert dran vorbeilaufen können. Eine sehr sichere Linsenhalterung ist ein kleiner Hohl-Stöpsel, mit Durchmesser 5.6 außen und 5 mm innen und natürlich einem Anschlag-Flansch am Anfang. Auch muß man die Länge ausmessen, bis zur Linsen-Position. Ineinandergesteckt fräst man den überstehenden Teil ebenfalls bündig ab und arbeitet den Schlitz mit einem 3 mm Fingerfräser nach. Bei hinreichender Sorgfalt bleiben die Teile zusammen, ohne daß man sie verkleben muß und so kann man alle Verbindungen später bei Bedarf auch wieder lösen.

Zusammengefügt schaut dann der Aufbau so aus. Links die Lichtquelle mit Zwischenraum für Filter, Aufweitungs-Optik, danach der Auslenkspiegel in Form eines Prismas. Das Bündel kommt aus dem unteren Prisma des Teilerwürfels, weswegen die Kante des Prismas ein klein wenig über die Diagonale des Teilerwürfels hineinragen kann. Rechts die Linse in ihrem Halter mit entsprechender Sicherung.

Noch etwas größer der eigentliche Interferometer-Teil, der prinzipiell nur diese drei Teile braucht. Die Lichtquelle hingegen ist ein ganz eigener, gesonderter Punkt, doch davon später.

Das Funktions-Prinzip
Wegen der Unterscheidbarkeit wurde die Informations-Welle, die den Prüfling ausleuchtet, hier grün dargestellt, während das Referenzbündel und die spätere Referenz-Welle nachfolgend rot dargestellt wurde. Entscheidend für das Interferieren ist, daß beide Lichtpunkte räumlich zusammenfallen müssen, weswegen beim Aufbau der Prüfanordnung nur dann ein Interferogramm entsteht, wenn diese Bedingung erfüllt ist. Das Funktions-Prinzip ist denkbar einfach, wenn man es mal verstanden hat. Lichtquelle ist in jedem Falle ein paralleles Lichtbündel, das oberhalb der Teilerfläche eines Teilerwürfels in zwei 50% / 50% Teilbündel zerlegt wird. Die grüneTeilwelle nach der Spiegelung wird von der 5 mm kleinen Linse zu einem Lichtpunkt fokussiert und bildet die Informations-Welle. Während die anderen 50% durch die Teilerfläche hindurch die Referenz-Welle bilden, rotes Lichtbündel.
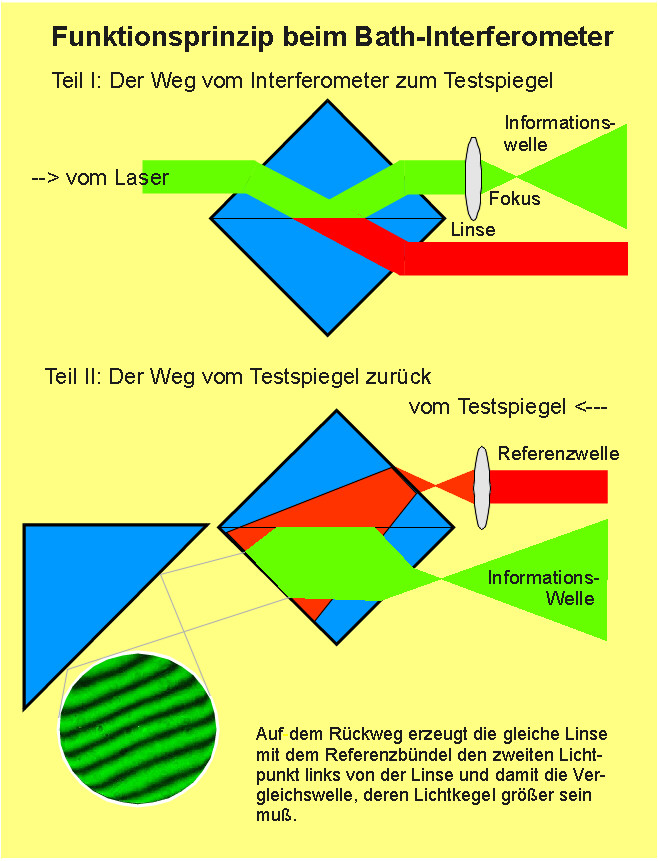
Bei der Justage des Bath-Interferometers sollte der Bündel-Abstand etwa 5-6 mm betragen, streng parallel zu einer Wand im Abstand von ca. 3-4 Meter verlaufen und nach dem Einfügen der kleinen Bikonvex-Linse sollte das unfokussierte Referenz-Bündel zentrisch zum als Lichtkegel aufgeweitete Informations-Bündel liegen, wie das folgende Bild zeigt. Das ist die große rote Kreisfläche, wie man sie im Abstand von ca. 40 cm auf einem Projektionsschirm sehen kann. Etwa im Zentrum erkennt man das kleine helle Referenz-Bündel, das erst auf dem Rückweg zur Referenz-Welle fokussiert wird, allerdings hinter der kleinen Linse, wie oben im Schemabild dargestellt.

Anmerkungen zur Lichtquelle
Der große Vorteil des Bath-Interferometeres ist, daß keine Kohärenz-Länge erforderlich ist. Bei Laserlicht mit einer langen Kohärenz-Länge interferieren oft bei Planplatten die beiden manchmal 30 mm und mehr Abstand entfernten Planflächen, was sich sehr störend bemerkbar macht, wenn man eine der Flächen prüfen will. Bereits mit Weißlicht, wie es von einer Autolicht-HalogenLampe erzeugt wird, kann man mit Hilfe des Bath-Interferometers über den gesamten Spektralbereich prüfen, wenn man enge Interferenzfilter dazu benutzt. Für diesen Zweck habe ich mir einen eigenen Interferometer für Weißlicht gebaut, dessen Parallel-Bündel über einen ca. 120 mm Fokus kleinen Achromaten erzeugt wird, um die nötige Genauigkeit zu bekommen. In den parallelen Strahlengang muß man dann die Interferenz-Filter stellen, wenn man z.B. den Farblängsfehler von Refraktoren ausmessen will. Die Laserdioden haben mehrere Probleme.
Meist ist das Bündel im Durchmesser zu klein mit 1-2 mm, weshalb man eine Optik zu Strahlausweitung bräuchte. Eine kleine Minuslinse mit ca. 500 mm Minus-Brennweite schafft bereits ein wenig Abhilfe und vergrößert das Referenzbündel nur geringfügig, sorgt aber für eines bessere Ausleuchtung der Bikonvex Linse. Die Laserdioden haben in der Regel relativ schlechte kleine Achromaten als Kollimations-Optiken. Bei Laserdioden wird ein heller Lichtpunkt über einen kleinen Achromaten in ein Parallel-Lichtbündel verwandelt. Das gibt es auch justierbar. Auch so könnte man das Bündel etwas variieren. Alles in allem sind die bezahlbaren Laserdioden eigentlich unbrauchbar, weil sie sehr viel Artefakte ins spätere Interferogramm einführen. Lediglich bei Weißlicht entstehen sehr saubere Interferogramme, die sich dann über das von uns entwickelte Auswertprogramm AtmosFringe sehr schnell auswerten läßt. Mittlerweile gibt es Lieferanten, deren Laser-Lichtbündel bis 7 mm Durchmesser aufgeweitet ist, leider aber ebenfalls noch Artefakte einführt.
Bei jedem neuen Interferometer muß ja geprüft werden, ob er auch die an ihn gestellten Anforderungen erfüllt. Deshalb ein Prüfspiegel 300/1500 mit einer hohen Qualität, die Strehl = 0.96 bekannt ist.

Da das Laserlicht nicht nur für die Augen schädlich ist, braucht man einen Graufilter oder zwei gegeneinander verdrehbare Polarisations-Filter, womit man das Licht stufenlos "dimmen" kann. Mittlerweile sitzt das Interferometer bereits auf einem Kreuztisch, den Ronny mitgebracht hat. Rechts im Bild sieht man die Auflage des KeplerFernrohres, das deswegen notwenig ist, weil der Fokus der DigitalKameras in der Regel so kurz ist, daß man an den Fokus des Interferometers nicht herankommt. wozu allerdings noch ein wichtiges Hilfsmittel hergesetllt werden muß: Ein verkleinerndes KepplerFernrohr von minus 0.8 fach. Auch für die Kontrolle mit dem Auge ist dieses verkleinernde Fernrohr sehr sinnvoll.

Zum Bau dieses Fernrohres nutzten wir zwei kleine 200 mm Achromaten vorne, die man mit der konvexen Seite zueinander stellt wie bei einem DialSight-Okular, siehe Übersicht. http://rohr.aiax.de/eyevar27.jpg Das wäre das Objektiv dieses verkleinernden Fernrohres. Im entsprechenden Abstand sitzt das "Okular", das aus zwei Achromaten besteht mit 250 mm Brennweite, die in gleicher Anordnung eingesetzt werden. Den richtigen Abstand bekommt man, wenn man auf den ca. 4 m entfernten Abstand des Prüflings fokussiert, und im übrigen soviel Spielraum einbaut, daß man alle diese Abstände realisieren kann. Um randscharfe Interferogramm zu bekommen, ist der richtige Abstand dieser beiden Teile, Objektiv und Okular, sehr wichtig. Jeweils vorne ist die Halterung des "Objektivs" zu sehen, am anderen Ende sitzt das Okular. Beide Teile werden von einem dünnwandigen Carbon-Rohr gehalten, was sich unlängst bei mir verirrt hatte. Im Normalfall reicht ein Kunststoff-Rohr aus, wie es bei der Installation verwendet wird. Man kann es innen mit Velour-Folie auskleiden. Hier ist also jetzt auch noch das verkleinernde Kepler-Fernrohr zu sehen, auf gleicher Bauhöhe von 9 mm zur Basis

Wie bekomme ich ein Interferogramm ?
Vorausgesetzt, das Interferometer wurde richtig zusammengestellt und justiert und sitzt auf einem Koordinaten-Tisch, der in drei Achsen (X-, Y- und Z-Achse) aussteuerbar ist. Zusätzlich sollte man den Tisch noch drehen können. DAnn richtet man das Laserbündel zunächst auf das Zentrum einer Optik, meist ein Newton-Spiegel, der beide Bündel in unterschiedlicher Weise zurückwirft. Das helle Referenz-Bündel kommt unverändert wieder zurück und kann zur Kontrolle auf die Fläche des Linsen-Halters projiziert werden. Das entspricht dem kleinen hellen Licht-Kreis in der rechten Bild-Hälfte. Dicht daneben links wird das Informations-Bündel etwas schwächer abgebildet. Das hängt damit zusammen, daß die Optik aus dem gesamten ursprünglichen Lichtkegel zu Beginn einen schlankeren Kegel ausschneidet. Je nach Abstand des Interferometers vom Prüfling liegt diese kleine Projektions-Fläche des Linsen-Halters außerhalb, ganz exakt oder innerhalb des Fokus, dieses Informations-Kegels bzw. der Informations-Welle. Da aber beide Teilwellen räumlich zusammengesetzt werden müssen, um zu interferieren, muß diese Projektionsfläche zwingend innerhalb dieses Fokus gelegen sein. Das bedeutet, man sucht sich genau den Fokus und schiebt anschließend das Interferometer noch ein paar Millimeter zum Prüfling, bis beide "Lichtscheibchen" etwa die gleiche Größe haben.
Da nun der Abstand Interferometer-Prüfling einigermaßen stimmt, und da auch das Licht-"Echo" vom Prüfling etwa in der richtigen Höhe liegt, also wieder ca. 9 mm zur Basis, schiebt man das Interferometer soweit quer zur X-Achse, bis das helle Referenz-Bündel exakt durch die Einzellinse fällt, damit es zum Lichtkegel hinter der Linse bzw. zur Referenz-Welle fokussiert werden kann. Das kann man nun beobachten im Auslenkspiegel, weil zwei kleine Lichtpunkte erkennbar sind. Dafür ist nun das Kepler-Fernrohr gut. Richtig ausgerichtet erkennt man den einen Lichtpunkt als den ausgeleuchteten Prüfling wieder, und drum herum die Referenz-Welle. Genau dort, wo man Licht von beiden Wellen bekommt, interferiert das Bild und man sieht ein erstes Interferogramm. In der Regel sind das erst einmal konzentrische Kreise, woran man erkennt, daß der Fokus noch nicht stimmt. Bei richtiger Fokussierung nimmt die Zahl der Ringe ab, oder die Ringe werden flacher, bzw. der Radius des Kreises größer, bis aus den Kreisen gerade Linien geworden sind.

Ein erstes Interferogramm mit dem neuen Bath-Interferometer an einem Newton-Spiegel ausprobiert. Bei einem Kugelspiegel sollten die Streifen parallel und schnurgerade sein. Links des Spiegels erkennt man Teile der Referenz-Welle, weshalb unten links klein eine Abbildung eingefügt ist: Die hellgrüne größere Kreisscheibe bildet die Referenz-Welle mit dem größeren Kegel, während das eigentliche Interferogramm gemeinsam aus Referenzwelle und Informations-Welle gebildet, deswegen auch heller sein muß und natürlich interferiert.

Um es nochmals zu wiederholen: Die Achse zum Spiegel ist die Fokussier-Achse, die QuerAchse dazu dreht die Interferogramme,während die Höhen-Achse die Anzahl der Streifen regelt. Fallen beide Lichtpunkte exakt zusammen, ist die Anzahl der Streifen sehr niedrig, liegt die Referenz-Welle über oder unter der Informations-Welle, erhöht sich sich Anzahl der Streifen wieder. Sinnvoll ist es aber, sich an eine Orientierung zu gewöhnen, z.B. grundsätzlich von oben, also mit einer großen Streifenanzahl zu beginnen und dann den Tisch langsam in der Z-Achse nach unten zu bewegen. Das ist bei der Beurteilung von Über- oder Unterkorrektur äußerst wichtig, aber auch bei Koma und Astigmatismus. Alle diese optischen Fehler haben typische Entsprechungen beim Interferogramm. Bei oberen Interferogramm hat man prinzipiell eine völlig überkorrigierten Kugelspiegel vor sich, der immer entsteht, wenn man eine Sphäre parabolisiert und dies vom Kürmmungsmittelpunkt aus beurteilt. Man hat es in diesem Falle mit einem divergent/konvergenten Lichtbündel zu tun und nicht wie am Himmel mit einem parallelen Lichtbündel. Mit der Strahlenoptik kann man sich diesen Sachverhalt leicht verdeutlichen.
schlußendlich der stolze Besitzer Ronny, der nun eine funktionsfähige Einrichtung zum Prüfen von Hohlspiegeln aller Art hat. Bis er mit den Feinheiten vertraut ist, wird noch einige Zeit vergehen.

#######################################################################################
ein Nachtrag zur Funktions-Weise von Interferometern allgemein:
01. Das Prinzip eines Interferometers beruht darauf, daß eine Lichtquelle in
zwei zusammenhängenden Teilwellen (50/50%) zerlegt wird. Diese Teilwellen
legen dann unterschiedliche Wege zurück und werden aber am Schluß wieder zusammen-geführt. Nun interferieren sie, weil sie auf dem Weg unterschiedliche Informationen erhalten haben.
02. Beim Bath-Interferometer nennen wir die Teilwelle, die zu Beginn die Bikonvex-
linse passiert hat, die Informations-Teilwelle, sie stellt einen Lichtkegel dar, und leuchtet die Optik aus. Die Referenz-Teilwelle durchläuft zu Beginn als dünnes Parallel-Bündel das optische System incl. aller opt. Komponenten wie Kollimations-Spiegel etc. und wird erst zum Schluß durch die gleiche
Bikonvex-Linse zur Referenz-Welle.
03. Beide Teilbündel durchlaufen also auf gleichem Weg das opt. System, bei einem Newton in der Reihenfolge:
IMeter-Parabolspiegel-Autokollimationsplanspiegel-Parabolspiegel-IMeter. Bei einem Flat mit Bohrung muß
das Referenzbündel in der Nähe der Bohrung vorbeilaufen, sodaß man immer zwei Lichtpunkte sehen muß,
nur dann funktioniert das Interferenz-Prinzip.

Ein paar Tipps: Man richtet den Testaufbau Parabolspiegel-Flat so ein, daß der Lichtkegel aus dem Fokus der
Parabel im Bereich der Planspiegelbohrung in jedem Fall einen kleineren Durchmesser hat, wenn man nicht
den Lichtkegel vignettieren will. Das überprüft man mit einem künstlichen Stern.
Den Testaufbau Parabel-Flat justiert man am besten mit einem Laser, der genau mit der Achse des Plan-
spiegels zusammenfällt. Das geht z.B. mit folgenden Kollimations-Zylindern, die man in die Bohrung einfügt:

Dabei muß der Anschlag-Rand - siehe roter Pfeil - mit der Bohrung in einer Aufspannung in der Drehbank
gedreht sein, also "laufen" wie man im Fachjargon sagt.
Der Justierlaser muß dann die Mitte des Parabolspiegels treffen. Der Parabolspiegel muß dann so justiert
werden, daß das Bündel wieder im Urspruch verschwindet.
Da diese Justage nicht ganz exakt ist, zentriert man an einem künstlichen Stern im Fokus der Parabel nochmals
nach. Eine Feinjustage erfolgt schließlich über das Interferogramm selbst über die Koma-Figuren.

###########################################################################################
Der folgende Beitrag war versteckt:
Lieber Wolfram,
Herzstück meiner Autokollimation ist ein Justierlaser, der exakt im rechten Winkel zur Planspiegelfläche positioniert ist.
Hergestellt wird der weiße Kunststoff-Zylinder in einer Aufspannung und der Justierlaser von Birkmeier muß stramm hinein-
gehen. Auch muß er exakt justiert sein. Von vorne sind das meine zwei Zylinder für meine beiden Planspiegel.

Wichtig dabei ist, daß die Anschlagfläche, siehe jeweils den roten Pfeil, mit der Mittenbohrung läuft. Diese Anschlagfläche
muß auf die Planfläche von vorne drücken, dann verläuft der Laserstrahl entlang der optischen Achse. Der übrige Zylinder
hat zur Bohrung ein Spiel von ca. 0.2 mm, also nicht kritisch.

Jetzt muß man nur noch dafür sorgen, daß man die optische Mitte vom Parabolspiegel erwischt. Wenn ich kann, schreibe
ich mit einem Folienstift einen ca. 4-5 mm kleinen Kreis auf die Spiegelmitte, nachdem ich die Scheibe auf einem Drehteller
exakt zentriert habe durch Rundlauf.
Wenn also der Abstand Parabolspiegel-Planspiegel so ist, daß der Lichtkegel noch locker durch die Bohrung kommt,
der Fokus liegt bei einem f/4 Spiegel ziemlich nahe an der Spiegelrückseite, muß man halt ausprobieren oder zeichnen,
dann verkippe ich lediglich den Parabolspiegel so lange, bis der Laserstrahl von der Mitte des Parabolspiegels wieder
im Ursprung zurückkehrt.
Weil das zwar gut geht, aber noch nicht genau genug ist, justiere ich im zweiten Schritt an einem künstlichen Stern
die Sache erneut, also noch genauer.
Und ganz genau wird die Sache, wenn man die Koma aus dem Testaufbau über einen Interferometer ganz genau
herausjustiert. Dann wirst Du viel Freude an allen übrigen Tests haben, also vor allem am Ronchi-Test und Foucault.
Das sind nämlich die wichtigsten:
Ronchi sagt was über die Korrektur und Foucault was über die Fläche, wenn der Planspiegel einigermaß stimmt, und
das scheint offenbar so zu sein.
E027 Zentrier-Schritte eines Refraktors vor dem Planspiegel-Flat, Kollimation Align
(A082 * Takahashi Super APO TSA 102N 816 erstes Test-Objektiv William FLT 110 versus TSA)
Zweitvermessung im Zusammenhang mit oberem Link
Je nachdem wie viel Arbeit man in die Vermessung investiert, fallen die Meßergebnisse in der Regel
leicht unterschiedlich aus, was auf Certifikaten mit der Bemerkung festgehalten wird: Gemessener
Wert und besser. In dieser zweiten Testreihe kommt beispielsweise ebenfalls ein geringfügig besseres
Ergebnis heraus. Der umgekehrte Fall ist ebenfalls möglich.
Mit ein Grund für das bessere Ergebnis ist eine sorgfältige Kollimierung des APO's vor dem Planspiegel,
was offenbar erst in einem Dreier-Schritt zu ganz exakten Ergebnissen führt:
A) die Kollimierung über einen Laser und dessen Reflex-Punkte ist als erster Schritt noch nicht
genau genug, weshalb
B) die Überprüfung über eine ganz feine Pinhole sinnvoll ist. Aber auch da gibt es noch
C) Koma-Restfehler, die man erst über ein Interferogramm gut erkennen kann.
Erst nach dieser Prozedur scheint man exakt auf der Achse zu sein, weil außerhalb der Achse
ein Objektiv mit anderen Fehlern reagiert: Mit Astigmatismus und Koma und einem anderen Farb-
längs- und Farbquerfehler.
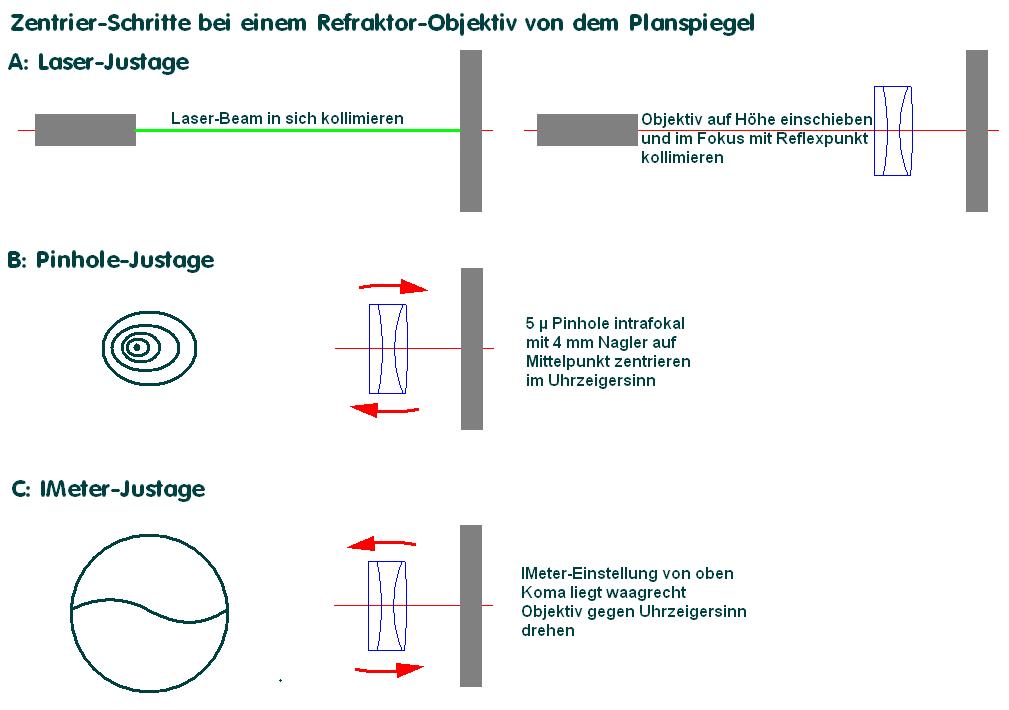
Beim Sterntest spielen auch die Helligkeit der Lichtquelle und die Kamera-Verschlußzeiten eine Rolle.

gleiches gilt für den Foucault-Test, der aber ziemlich dem entspricht, was ich bereits im 1. Durchgang
ermittelt habe. Komabedingt fällt die Messung des Farblängsfehlers um einen kleinen Wert besser aus.
Statt RC_INdex = 0.1931 käme im zweiten Durchgang 0.1431 heraus. Die Reihenfolge der Farben wäre
diesmal blau-grün-rot-gelb, vorher blau-rot-grün-gelb. Man kommt trotz Reihenmessung an die Grenze
dessen, was sicher meßbar ist. Interessant auch der mittlere Streifen beim Weißlicht-Interferogramm:
Für mich ein Ausdruck des Gaußfehlers, da Blau die größte Überkorrektur hätte und damit ein
Unterscheidungs-Kriterium für den Gaußfehler und dessen Größe. Auch würde sich die Reihen-
folge der Farben abbilden: Gelb ganz hinten (beim mittleren Streifen oben) Blau ganz vorne
(beim mittleren Streifen unten)


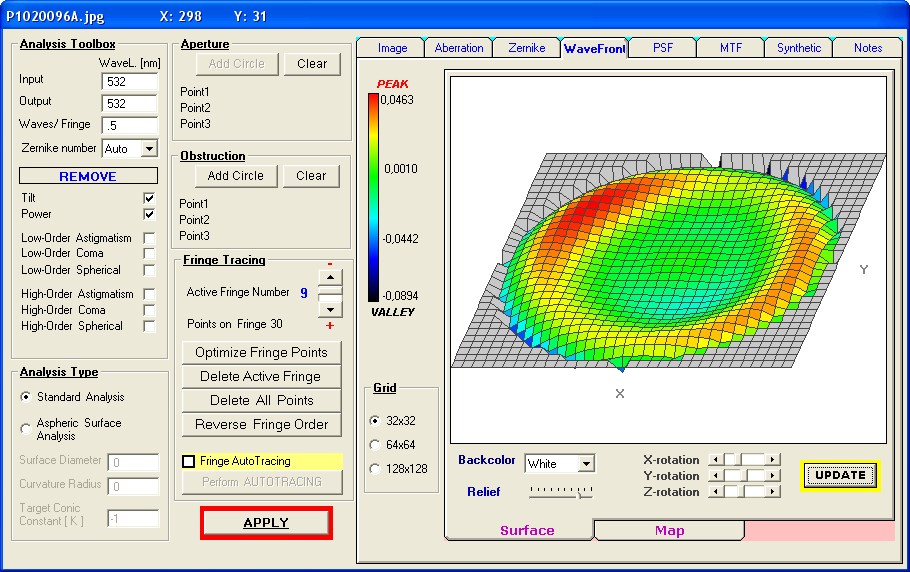
der Strehl springt bei Grün von 0.967 bei 546.1 nm wave im 1. Durchgang auf 0.981 bei 532 nm wave im 2. Durchgang
Das wäre eine Verbesserung um 1.4% Strehlpunkte, die auch ein Ausdruck der Toleranz darstellt, in der diese
Messungen stattfinden.
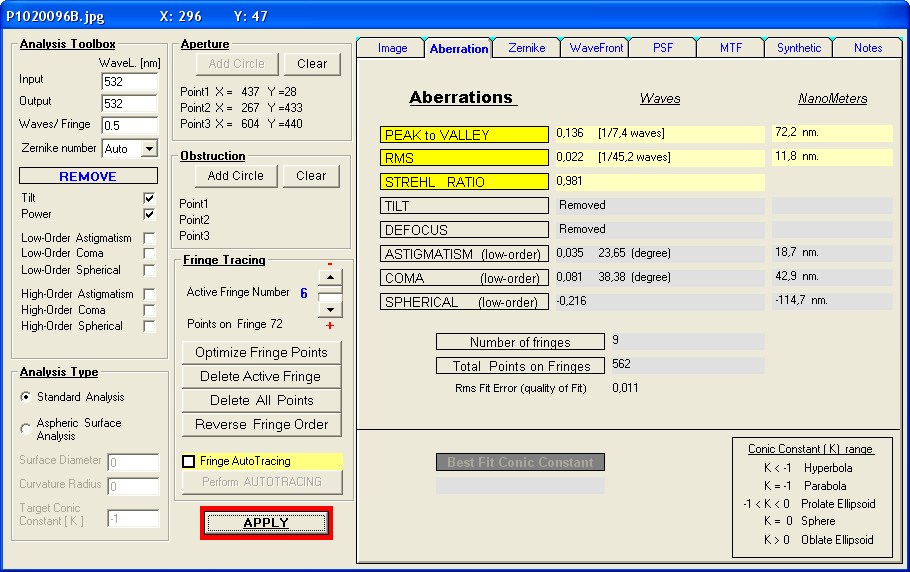
E026 Zentrieren oder kollimieren
* Kollimierung - Objektiv-Achse muß mit Tubus-Achse zusammenfallen
* Zentrierung - Verkippung von opt. Einzel-Elementen beseitigen
Die Begriffe sind nicht scharf ab gegrenzt: Bei einer Linse sucht man beim Zentrieren beispielsweise den opt. Mittelpunkt
und schleift den Rand entsprechend nach. Dann dürfte auch der Keilfehler der gleichen Linse gegen Null gehen. Bei einem
Doublet werden zwei Linsen über Abstandsplättchen ebenfalls zentriert. Es darf also auch keine Verkippung der beiden Linsen
zueinander vorhanden sein. Andernfalls reagiert ein Zweilinser mit Koma oder Achskoma, also mit Koma-Figuren, wie man sie
von einem Newton-Teleskop im Bildfeld kennt. Will man also ein Objektiv exakt auf der optischen Achse zentrieren, dann
muß dieses Objektiv exakt auf der opt. Achse sein, man würde sonst die Abbildung dieses Objektivs im Bildfeld bekommen,
und das hat bekanntermaßen andere Bildfehler, die mit der Abbildung auf der opt. Achse nichts zu tun haben.
Beispiel für Bildfehler im Feld eines Refraktors
Wenn ein Refraktor Astigmatismus zeigt, dann kann das auch damit zu tun haben, daß er nicht exakt auf der optischen
Achse untersucht wird. Am Beispiel eines FSQ im nächsten Bild kann man das studieren: Hier mischt sich im Bild-Feld
Koma+Astigmatismus
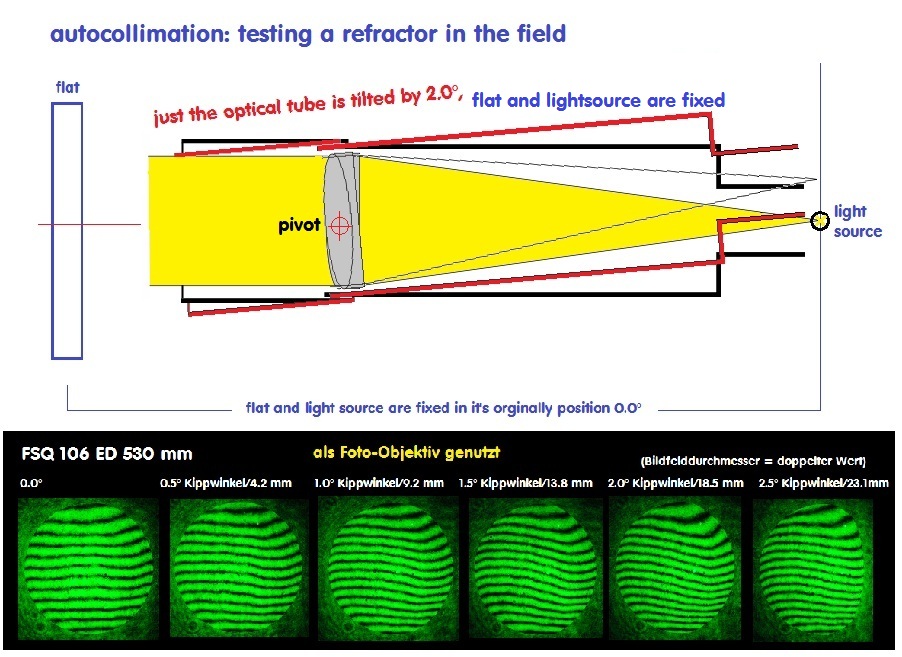
siehe auch Artificial Sky Test im Bildfeld, field, Verkippung des Tubus
Der Unterschied zwischen beiden Begriffen läßt sich über folgende Übersicht zeigen: Im oberen Bildteil hat man es mit einer
fehlerhaften Kollimation zu tun, die man über einen Reflexbild-Kolliimator korrigeren kann. Selbst wenn das Objektiv exakt zum
Tubus kollimiert worden ist, hat das Objektiv für sich immer noch einen Zentrierfehler, den man über die Achskoma erkennt.
Jetzt nützt aber nur noch ein künstlicher Stern von 15µ und kleiner exakt auf der Achse unter hoher Vergrößerung, um jetzt das
Objektiv zu zentrieren. Dazu haben manche Optiken kleine Zentrierschrauben, die man nach bestimmten Regeln benutzen muß.
Allerdings sollte man diese Regeln auch kennen, da sonst ein größerer Schaden entstehen kann. Man muß also wieder unterscheiden:
a) zur Tubus-Achse ist das Objektiv perfekt zentriert, [Hilfsmittel GRZ-Kollimator]
b) das Objektiv selbst hat aber noch Koma ! [Hilfsmittel künstlicher Stern, hohe Vergrößerung, exakt auf opt. Achse]
Siehe auch http://www.fernrohr-service.de/4.html , www.astro-fotos.com/pdf/anleitung-refraktorkollimation.pdf

Dies ist ein weiteres Beispiel für eine erfolgreiche Kollimierung, bevor man anschließend das Objektiv selbst zentriert.
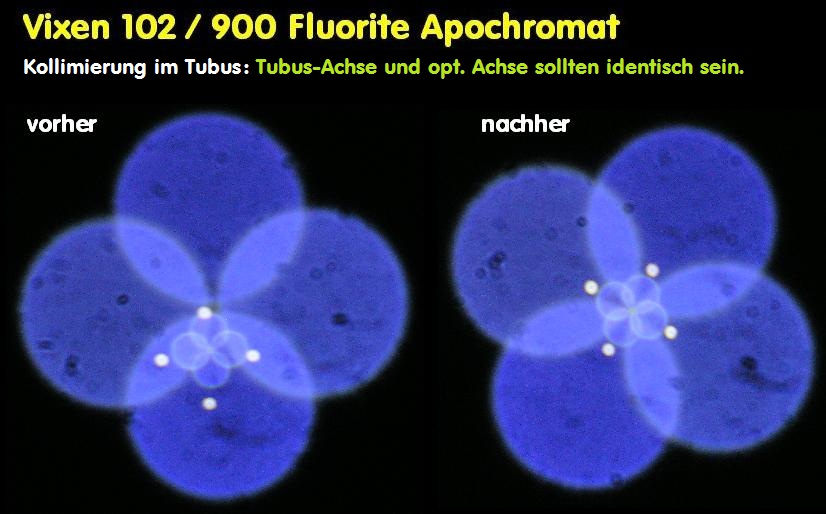
Bei der Kollimierung benutzt man die Reflexbilder der Einzelflächen. Ausgehend von einem Kollimator (es kann ein Chesire-
Okular, ein einfacher Laser oder der GRZ-Kollimator sein) muß die Lichtquelle, das Objektiv und schließlich der Autokollimations-
Planspiegel auf einer gemeinsamen Achse sein. Das erreicht man in jedem Fall über die Reflex-Bilder, die idealerweise alle in einem
Fokus-Punkt zusammen fallen sollten. Erst wenn dies der Fall ist, kann man die Zentrierung des Objektivs bei hoher Vergrößerung
und einer möglichst feinen Pinhole sicher beurteilen. Eine Zentrierung des Objektivs über die Reflex-Bilder ist deshalb prinzipiell
unmöglich, weil die erforderliche Genauigkeit viel zu gering ist.
Zentrieren eines opt. Systems
Auch wenn ein Zweilinser perfekt zur Tubus-Achse über Reflexbilder kollimiert worden wäre, kann er immer noch heftige Achskoma
haben, weil die Objektiv-Linsen selbst zueinander deutlich verkippt sind. dann sieht man Komafiguren, wie im folgenden Beispiel. Und
je nach Objektiv-Typ braucht man eine Regel, nach welchem Kipp-Verfahren die Einzellinsen zu behandeln sind. Bei einem Zweilinser
wird man das über die PLättchen-Dicke beeinflussen, bei einem Triplett über vorhandene Zentrier-Schrauben, wobei in der Regel
nur die mittlere Linse in Richtung Koma-Kern oder in Richtung Koma-Schweif verschoben werden muß. Man muß sich vorher ver-
gewissern, nach welcher Regel das beim jeweiligen Objektiv-Typ funktioniert. Jedenfalls gibt es immer wieder wißbegierige Finger,
die uns mit völlig dezentrierten Optiken hinterher hilfesuchend um Rat fragen.
In einem anderen Fall lag die Dezentrierung daran, daß der Druckring der Fassung ganze 1 mm Spiel hatte, und die Einzellinsen nach Herzenslust im Objektiv
verkippen konnten. Erst als dieses Spiel behoben war, ließ sich das Objektiv über die seitlichen Zentrierschrauben wieder steuern. Der Händler hat offenbar
bis heute nicht eingesehen, daß man solche Optiken besser nicht verkauft. Auch hier sieht man die Koma-Figur deutlich, die ein dezentriertes Objektiv zeigt.

Bei vielen katadioptrischen Systemen wie Schmidt-Cassegrain oder RC-Systemen führt die Dezentrierung des Hauptspiegels zu Astigmatismus, wie man ihn beim
Artificial Sky Test sehr gut sieht. Hier muß nach einem bestimmten Verfahren der Hauptspiegel exakt zentriert werden.

Beim nächsten Beispiel rechts im Bild wäre der Sekundärspiegel nicht ganz exakt zentriert. Es ist wieder der Artificial Sky Test, der bei Höchstvergrößerung die genauesten
Bilder abliefert: Der 1. BeugungsRing müßte exakt um das Maximum geschlossen sein. Das Interferogramm wird also Restkoma zeigen.
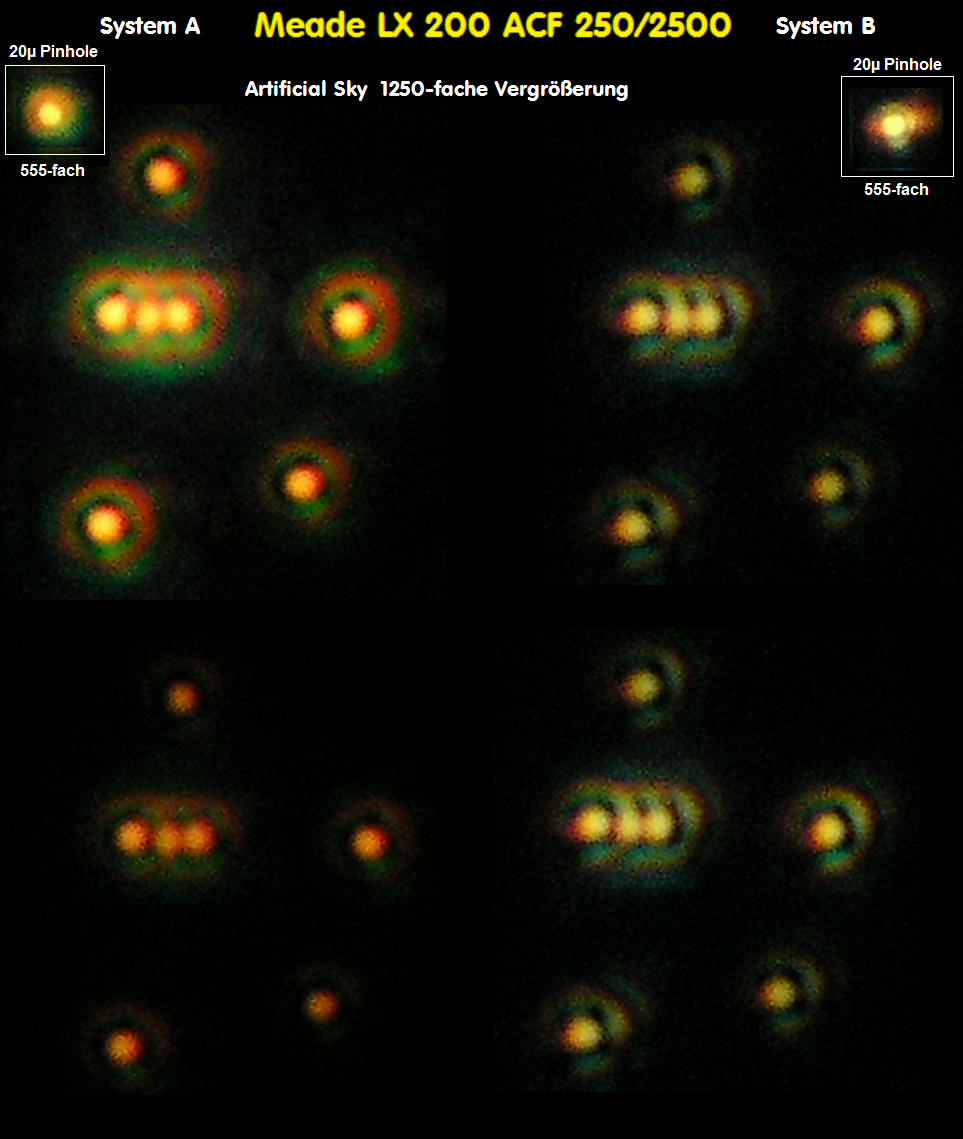
Wenn ein Objektiv nicht exakt vor einem Planspiegel "kollimiert" worden ist, dann bekommt man wegen der Verkippung zum Planspiegel die Abbildung, die ein
Objektiv im Bildfeld hat. Das kann man auch gezielt einsetzen, wenn man sich die Abbildung einer Optik im Feld betrachten will. In diesem Fall reagiert
das Objektiv mit einer Mischung aus Koma und Astigmatismus. Das ist aber nicht repräsentativ für die Abbildung auf der opt. Achse.
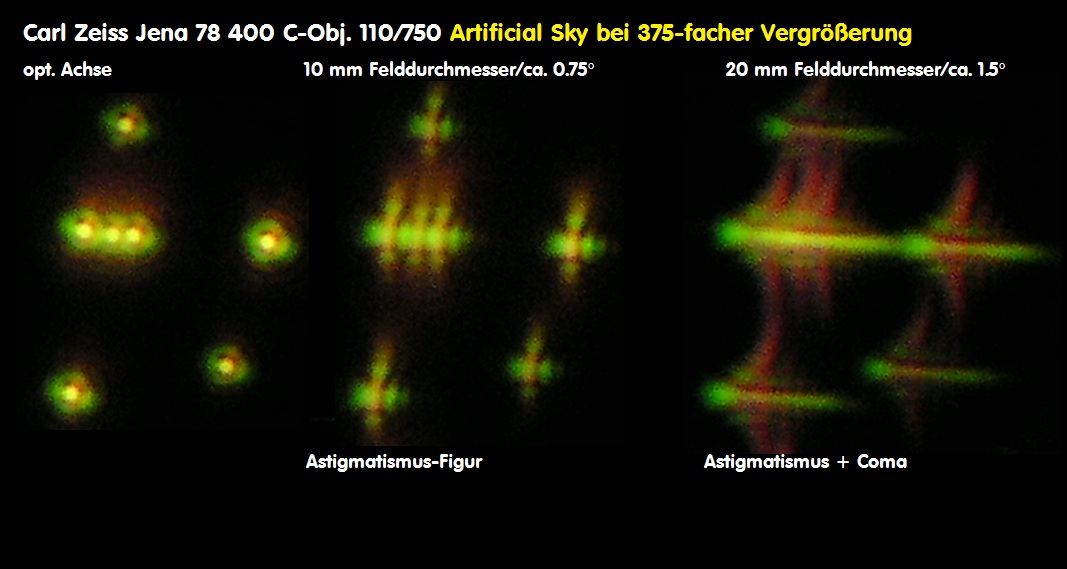
Weitere Berichte sind hier zu finden. http://www.astro-foren.de/showthread.php?6084-Verzeichnis-optischer-Berichte
TMB FH 203/1800 mehrmals nachgebessert
Bei Durchsicht meiner bisherigen Berichte finde ich sicherlich noch weitere Beispiele.
E025 Visuelles Stern Interferometer - Simulation am Kugelspiegel Sphäre
Visuelles Sternen Interferometer
Es ist ein Bericht in SuW von 4/1999, der mich bereits damals sehr beeindruckte. Unlängst klang dieser Effekt in
einem der Beiträge an, weshalb ich dieses Thema "nachliefern" wollte. Die Grundlage für weitere Versuche wäre
der folgende Link. An einem Kugelspiegel läßt sich dieser Effekt schön demonstrieren.
Ein visuelles Sterninterferometer im Eigenbau Uni Wien
Quote:
Ein visuelles Sterninterferometer im Eigenbau
Hochgenaue Doppelsternabstände mit einfachsten Mitteln
Von Franz Kerschbaum
Ein einfaches Sterninterferometer in Form einer auf das Fernrohr aufgesteckten Blende wird vorgestellt, Damit wird nicht nur die
Wellenlängen- und Öffnungsabhängigkeit der Fernrohrauflösung leicht erfahrbar, es lassen sich auch Doppelsternabstände mit
mittelgroßen Amateurfernrohren (Öffnung = 20–30 cm) auf wenige hundertstel Bogensekunden genau bestimmen.
Man braucht nur einen Kugelspiegel mit zwei kleinen Aperturen am Rande abzublenden. Die Lichtquelle wäre ein künstlicher Stern
und weil es die gleiche Licht-Welle ist, die in zwei Teilwellen zerlegt wurde, interferiert dies auch im Labor. Auch mit einem
Parabol-Spiegel müßte das gehen, da die Abweichung zur Sphäre über die kleine Fläche relativ gering sein müßte.
Je kleiner also die Pinhole ist - bis zu 5 micron klein - umso deutlicher sind die Interferenz-Linien. Seine Anwendung findet diese
Technik im interferometrischen Zusammenschluß vieler Großteleskope und in der Radio-Astronomie.
http://www.uni-protokolle.de/Lexikon/Interferometer_(Radioastronomie).html
http://www.astro.uni-jena.de/Teaching/Praktikum/pra2002/node103.html
http://de.wikipedia.org/wiki/Interferometrie
http://www.heise.de/tp/r4/artikel/16/16231/1.html
http://de.wikipedia.org/wiki/Very_Long_Baseline_Interferometry
http://www3.interscience.wiley.com/journal/103526821/abstract?CRETRY=1&SRETRY=0
http://www.fachportal-paedagogik.de/fis_bildung/suche/fis_set.html?FId=624560

Die Größe des Lochdurchmessers beeinflusst ebenfalls die Abbildung, man könnte den Sachverhalt sehr viel gründlicher unter-
suchen.

Mit einem Lichtspalt geht das ebenfalls, wenn er auf 10µ Breite eingestellt ist und weniger.

E023 Roland Christen zum Star-Test bei Maksutov-Systemen
Star Testing Complex Optical Systems
by Roland Christen
--------------------------------------------------------------------------------
I should start out saying that I have the highest regard for Suiter
and his book, there are however enough holes in the book vis a vis
refractors and catadioptrics that it cannot be used for all
occasions. If you want to see some wildly or perhaps mildly
asymetrical printouts, contact TEC Telescopes. They can send you some
Zemax results of Mak-Cass designs that may want you to start
nibbling.
Now on to my soapbox: The situation with the star test is more
complicated than manufacturers being afraid to be found out now that
amateurs have an easy test to evaluate the optics. When the optical
system gets more complex than a simple parabolic mirror, then there
are inherent aberrations that affect the star test. An example is the
Maksutov Cassegrain. This system can be manufactured many different
ways, but one popular way is to have all surfaces spherical, which
cuts down the need for hand work. Machines exist now that can lay
down a 1/20 wave or better spherical surface on a piece of glass
without any human intervention. In this pure form, the Mak-Cass has
left over 5th order aberrations and, depending on design, these can
be less than 1/10 wave on the wavefront. By the way, fast Apo
refractors have these same aberrations also. The RMS value will be
better than 1/50 RMS and the Strehl ratio will be exceedingly high.
In other words, the optic will deliver a very high contrast image,
consistent with the high wavefront rating. When tested on the night
sky, the inside and outside diffraction patterns will be quite
different. Any beginner will see it so and may conclude that the
optic is of poor quality.
As an example, I have recently finished exhaustive tests of different
10" F14 Mak-Cass systems, some with these inherent aberrations left
in, some with them meticulously removed. All the optics tested
between 1/10 and 1/12 wave with Strehl ratios of 98% or better. The
system with the uncorrected or pure Maksutov curves had the central
hole of the donut break out 4 times farther on one side of focus than
the other. It would be judged by the Suiter star test method as being
maybe barely 1/4 wave, if that. The hand aspherized version, which
was no better on the interferometer and had similar Strehl ratio,
showed a donut breakout approximately at the same point on either
side of focus - in other words textbook perfect. At focus, both
scopes showed a tight central Airy disc with a faint first
diffraction ring. At focus, it was impossible to tell them apart. The
ratio of brightness of the Airy disc and first diffraction ring was
essentially identical. Both scopes showed the same high contrast on
Jupiter and Saturn. Both scopes could split doubles with equal
precision.
This same thing happens in my short focus Apo triplet lenses. They
also have classical 5th order like Mak-Cass systems. I have seen
literally thousands of star patterns on my test setups. I can tell
you that the shadow breakout difference is almost entirely due to
slight increase in focal length of the very inner zones on these
optics. That is one half of the 5th order defect. This causes no
problem in definition and contrast for 2 reasons. 1, there is very
little energy as you go toward the middle of the optic, and 2, the
depth of focus approaches infinity at the very center. However, the
shadow breakout is linear, not asymtotic like the encircled energy.
This is easily fixed, of course by commercial makers by simply making
a large central obstruction.
The other half of the defect occurs at the outer zone. If this is
left uncorrected, you will see fuzz in the in-focus image which is
highly destructive of contrast. The inside and outside patterns will
look the same, causing you to conclude that the optic is textbook
perfect. It is this outer zone that the competent optician will
concentrate on, since this is the place that contributes most to the
definition, resolution and contrast of the optical system, even
though it has little or no effect on the inside/outside star pattern,
particularly where the shadow breakout occurs.
In view of the above, I have seen amateurs at star parties wrongly
interpret the star test and overestimate the quality of one optic
that was really not that good, and underestimate another that was
really superb.
I think all manufacturers will agree that the star test must be
properly done to place a VALUE on the correction. This is not so easy
with certain types of defects, and so the star test, when improperly
interpreted by untrained individuals, can overestimate and also
underestimate the actual quality. If you ask any reputable maker of
complex optical systems, they will agree that the interferometer will
give the most reliable result. Since Peter Ceravolo will not get on
SAA, I will paraphrase what he has told me time and again : You
cannot rely on anything but the interferometer to give you a
wavefront NUMBER. The interferometer takes no prisoners.
In my experience, when an optic measures 1/10 wave AT THE DESIGN
WAVELENGTH, then the performance will be nothing short of stunning.
Peter's criterion was a bit less at 1/8 wave P-V. Either way, the
customer will have an excellent optic.
By the way, Ceravolo is my mentor on testing of optics. Even though I
have been making optics for a long time, without his guidance in the
testing lab, I never would accomplished what I did. And yes, I used
to use the star test in the distant past when I made longer
refractors. Some of my optics came out good and have surprised me
when retested on the interferometer. But for the fast F6 and F7
triplets I make now, the star test falls short.
The dilemma for manufacturers then is, should we do our best to
produce smooth high contrast optics, or should we please the star
test crowd and do some hand aspherizing to get a more pleasing
out-of-focus star image? I can tell you that it is easy to do some
rough compensation with quick local polishing at several zones to get
more equal inside and outside star patterns, but the result will
almost certainly be a loss of contrast. Add to that a nice big
central obstruction to get rid of the offending inner zones, and
presto! you have a nice "fast food" Mak-Cass that doesn't work any
better than a typical SCT.
In our case, we will do our utmost to produce the closest faximile to
the star patterns in Suiter's book, but they will never be exactly
equal. The overriding concern will be that the optic has a very
smooth and accurate wavefront to produce the highest contrast
possible in the final image, which I assume will be in focus.
Roland Christen ASTRO-PHYSICS
--------------------------------------------------------------------------------
Return to Roland Christen Images and Essays.
E022 Sterntest bei obstruierten (perfekten) Systemen
Lieber Michael Korff-Karlewski,
mit dem Suiter Buch habe ich so meine liebe Not.
Warum?
Weil Computer-generierte Sternscheibchen-Tests höchst selten mit der viel differenzierteren Wirklichkeit
am Himmel oder auf der opt. Bank etwas zu tun haben. Dieses Buch stiftet mehr Verwirrung, als daß es
hilft, optische Fehler aufzudecken.
Für Refraktor-Optiken ist der Stern-Test nur sehr eingeschränkt verwendbar. Es fehlt die Farbinformation.
Dort wären der Farblängsfehler, fehlerhafte Zentrierung und eventuell der Gaußfehler gesondert und vor
allem farbig zu würdigen, was dieser schwarz-weiß-Test nicht hergibt. Mein Wissen um opt. Fehler beim
Sternscheibchen-Test resultieren aus den vielen praktischen Tests, aber ganz bestimmt nicht deswegen,
weil ich dem Suiter vertraue, der übrigens vor mir liegt.
Es läuft prinzipiell auf die Verabsolutierung eines einzigen Tests hinaus ohne irgend eine Gegen-
kontrolle. Und das lehne ich grundsätzlich ab. (Die meisten Händler und Sternfreunde haben in der Regel
nichts anderes zur Beurteilung, weswegen dessen Bedeutung überdimensioniert wird.)
Der Sachverhalt läßt sich ganz einfach simulieren. Ein nahezu perfekter Kugelspiegel sollte beim Sterntest
intra/extrafokal keine großen Unterschiede zeigen. Wenn man die Mitte mit einer Scheibe obstruiert, hat
man prinzipiell ein perfektes SC-, Cassegrain-, RC- oder Maksutov-System vor sich. Jeweils perfekt.
Erzeugt man mit diesem Setup die bekannten Sternscheibchen, bekommt man dieses Ergebnis, was ich so
interpretiere, daß keine signifikanten Unterschiede erkennbar sind. Alles andere wäre Kaffeesatz-Leserei.
Siehe auch hier:
http://www.astro-foren.de/showpost.php?p=34661&postcount=2
Je größer die Obstruktion, umso mehr Energie verlagert sich in die BeugungsRinge. Das wäre der einzige
Effekt, der sich auf die Sternscheibchen auswirkt.



E013B praxis-ferne Strehl-Diskussion-Einflußgrößen
Strehl-Begriff
Strehlwert und Obstruktion
Strehl und Temperatur - wenn sich Spiegel durchbiegen
RMS-Wert in Strehl-Wert umrechnen
Sie stirbt nicht aus, diese Art Diskussion, die Frage, wie man sich den Strehl vorstellen soll:
http://forum.astronomie.de/phpapps/ubbthreads/ubbthreads.php/ubb/showflat/Number/441023#Post441023
Der alltäglichen Strehl-Killer ist bei einem perfekt glatten und ausgekühlten Spiegel die Luftunruhe - auch Seeing
genannt. Nur 4-5 mal pro Jahr wäre ich in der Lage, die hohe Qualität meiner Dobsons am Himmel auch realisieren
zu können. Saturn und Orion-Trapez Stern E und F sind meine Zeugen.
Der nächste und bösartigste Strehl-Killer überhaupt ist ein mehr oder wenig großer spiegel-eigener Astigmatismus.
Den erkennt man wiederum nur bei besten Bedingungen und hoher Vergrößerung ab L/3 PV im Zenit. Bei richtiger
Positionierung des Spiegel (von einigen Herstellern deswegen mit einer Oben-Markierung versehen) lagert sich je
nach Neigung ein Teil wieder heraus.
Ein weiterer Strehl-Killer ist die Rauheit, oder Welligkeit, Ripple oder Micro-Ripple, welche Begriffe man immer dafür
verwendet. Zonen und abgesunkene Kante gehören dazu, die abgesunkene Kante blendet man einfach ab. In jedem
Fall verlagert sich die ankommende Energie in den ersten oder die weiteren Beugungsringe und reduzieren den Strehl-
Wert.

Ein weiterer Strehl-Killer ist die thermische Situation des Glas-Körpers, der nur im Idealfall die perfekte Parabel einhält.
Deswegen sind gute Spiegel unterkorrigiert und über die Unterkorrektur ein Strehl-Killer, weil man von einer konischen
Konstante von -1 für die Parabel ausgeht. Spätestens hier läuft die Strehl-Diskussion regelrecht an die Wand: Man
kann es wunderbar simulieren: http://astro-foren.aiacs.net/showthread.php?t=4332 Wenn man nämlich das Inter-
ferogramm eines ausgekühlten, aber unterkorrigierten Spiegels auswertet, dann drückt genau diese notwendige
Unterkorrektur den Strehl-Wert und den "Steinbeißern" ist schwer vermittelbar, daß diese Situation sogar besser ist.
Das Tubus-Seeing ist ein weiterer Strehl-Killer, (der astigmatische Fangspiegel ohnehin) und wer weiß denn so genau,
ob sein Newton-System immer exakt justiert ist?
Solange also der Strehl-Begriff losgelöst von der Rauheit und dem Astigmatismus diskutiert wird, kommt
immer ein schiefes, praxis-fernes Ergebnis heraus.
Im Idealfall ist die gesamte Energie im Maximum konzentriert, wie die 3D-Funktion zeigt, bei Störungen verlagert sich
die Energie immer vom Maximum in die Beugungsringe, wie man am künstlichen Sternhimmel sehr gut zeigen kann, zu
Lasten von Kontrast und Definition.

http://www.astro-foren.de/showthread.php?p=33608#post33608
Im Angesicht all dieser Einflußfaktoren, die unter Aufbietung aller fachlichen Resourcen in die Kreuz und Quer
breitgetreten und ausgelutscht worden sind, erscheint mir die ständige Wiederholung dieses Themas ein Ausdruck
großer Langeweile zu sein.
E013 Strehl-Begriff und Info
Manchmal findet man nix mehr ...
ein paar nützliche Informationen zum Strehl Begriff:
Dr. Karl Strehl - Fränkischer Gelehrter, Physiker und Optiker von Weltruf
http://www.kurt-hopf.de/astro/strehl.htm
http://www.kurt-hopf.de/astro/strehl-links.htm
http://wissenschaft-online.de/abo/lexikon/optik/593
###########################################################################
RMS-Wert in Strehl-Wert umrechnen
Zunächst eine Tabelle, die in ZEMAX über die conische Konstante bzw. Unterkorrektur einer Parabel simuliert
wurde. Sie enthält also Strehl, PV und RMS gleichermaßen und gilt für Wellenfront, nicht für Oberfläche.
RMS-Wert in Strehl-Wert umrechnen
Dem Günter sei Dank, daß er mich wieder einmal auf folgendes Thema gestoßen hat, das man locker mit dem Taschenrechner lösen kann.
Nämlich die Umrechnung eines RMS-Wertes in den Strehl-Wert:
Beispiel: Ein RMS-Wert von 0.022 soll umgerechnet werden.
1. Schritt: (2*3.141592654*0.022)^2 = 0.019107554
2. Schritt: Vorzeichen wechseln ......... - 0.019107554
3. Schritt: 2nd e hoch x drücken ........ 0.981073838
Und weil bei diesem hohen Strehl-Wert der PTV-Wert der Wellenfront von 0.095 unter Lambda/10 liegt, ist das Ergebnis
sehr plausibel. Der Blick durch das Teleskop dürfte ein übriges verraten. Bei einem Refraktor nützt aber ein hoher Strehl-
wert im grünen Spektrum gemessen noch nicht allzu viel. Erst wenn das sekundäre Spektrum dieses kleinen TMB APO's
80/600 in der Gegend von 0.02 mm zwischen Blau und Rot liegt, hat man einen sehr wertvollen kleinen Apochromaten
vor sich. Über das sekundäre Spektrum wird nämlich Unschärfe eingeführt, was man ganz deutlich bei Fraunhofer-
Teleskopen nachweisen kann. Mit einem Synta 150/1200 z.B. schaut das im Vergleich zu einem APO grausam aus.
E011 Caustik-Test Links und Literatur
Der 5-Meter-Spiegel auf dem Mount Palomar wurde seinerzeit auch mit dem Caustic-Test vermessen. Dieses hochgenaue Verfahren
(Lambda/50 der Wellenfront), mißt primär die Winkelabweichung einander gegenüberliegender Lichtbündel aus Zonen gleicher Einfalls-
Höhe. Die Krümmungs-Mittelpunkte der einzelnen Zonen liegen auf einer astgabel-förmigen Kurve, der Caustic, und sind definiert durch
den Term:
Xh=3*hz*hz / (2*R) und Yh=2*hz*hz *hz/ (R*R)
Xh bzw. Yh sind die jeweiligen Soll-Werte der Caustic, auf der die Krümmungsmittel -punkte der Zonen liegen. "hz" der Wert
der jeweiligen Zone vom opt. Mittelpunkt gemessen. Xh bzw. Yh sind Differenzwerte, man eicht den Koorodinaten-Tisch am
besten auf die 0.7% Zone, weil sich die am sichersten bestimmen läßt.
 (Darstellung nach ATM-Book III, 432f, "The Caustic Test) |
Bei diesen Gleichungen ist der ca. 0.02mm breite Lichtspalt fest mit dem Messmikroskop verbunden, er bewegt sich also
mit , das die Distanz der Abbildung des Lichtspaltes mißt. (1. Meßverfahren) Praktischer ist die Technik "erstes Licht - letzter
Schatten" (2. Meßverfahren), das mit der Messerschneide wie beim Foucault- Test ebenfalls die Distanz der Causticpunkte der
einzelnen Zonen vermißt. Mit Hilfe eines Koordinaten-Meßtisches werden die Xh-Werte "angefahren" und passend dazu die Ab-
stände Yh vermessen. Die erforderliche Genauigkeit bei Xh ist 0.01 mm, bei Yh muß mit 0.001 mm gemessen werden. Die
Eichung des Meßsystems erfolgt über eine mittlere Zone: Der Xh-Wert wird auf dem Meß-Schlitten eingestellt. Dieser wird
danach solange auf der Achse zum Spiegel vor und zurück bewegt, bis der Yh-Wert zur Zone paßt. Sicherheits- halber macht man
diese Messung auch noch für eine andere Zone. Nie beim Rand bzw. in der Mitte beginnen, da beide Zonen schwieriger zu bestim-
men sind. Wichtig ist, daß die Abbildung des Lichtspaltes, über den Lichtspalt gelegt wird, damit nicht die störende Koma der Par-
abel in das Meßergebnis einfließt. Auch muß mit einer starken Lupe auf Parallelität von Lichtspalt-Abbildung zur Messerschneide
geachtet werden, da sich sonst die Messung "verschmiert". Ein weiteres Hilfsmittel ist ein hinter der Messerschneide angebrachtes
kleines Kepler-Fernrohr mit ca. 3-facher Vergrößerung, das auf den Spiegel scharf eingestellt wird. Die Zonen markiert man
sinnvollerweise über ein Lineal, das man vor den Spiegel stellt und mit Zonen-Markierungen versieht, damit man tatsächlich
auch exakt die Zonen trifft. Ähnlich wie beim Foucault-Test tritt bei Bewegungen von 0.001 mm in der Yh-Achse bereits deut-
lich ein erster Licht-Schein hervor, während in der gegenüberliegenden Zone auf das Ver- schwinden des letzten Schattens
geachtet werden muß.

Das Datenblatt zeigt die Auswertung einer Meßreihe, deren Daten unter Xh u. Yh zu finden sind. Während die Xh-Werte den Soll-
Werten entsprechen, sind die Yh-Werte die tatsächlich gemessenen Ist-Werte, größer, gleich, kleiner den Yh-Soll-Werten. Die fein
punktierte Linie stellt dieses Abwei- chung nach oben bzw. unten von der geraden Null-Linie dar. In einem iterativen Verfahren wird
im zweiten Schritt auf die Deformation der Oberfläche und abhängig davon auf die Abweichung der Wellenfront geschlossen, und
in der durchgezogenen "Kreis"-Linie dargestellt. Damit ergeben sich auch alle anderen Werte, wie PV, RMS und Strehl. Die hohe
Genauigkeit ergibt sich aus dem "Hebelarm", der eine geringfügige Verkippung der Oberfläche in der Zone selbst auf die Abweichung
des gespiegelten Bündels im Abstand R hat. In unserem Meßbeispiel hat mein 16"-Meadespiegel bis zu einem Durchmesser von
ca. 320 mm eine Oberfläche von ca. Lambda/20 Wave, während ab dieser Zone der Rand bis auf Lambda/4 "herunterfällt". Dies
ergibt einen zweiten Fokus aus dieser Zone, der den Kontrast erheblich stört. Durch eine Ringblende kann dieser Teil abgeblendet
werden, wenn es um superscharfe Planeten-Bilder geht.
Weitergehende Links und Literatur:
http://www.marty-atm.de/caustik.htm
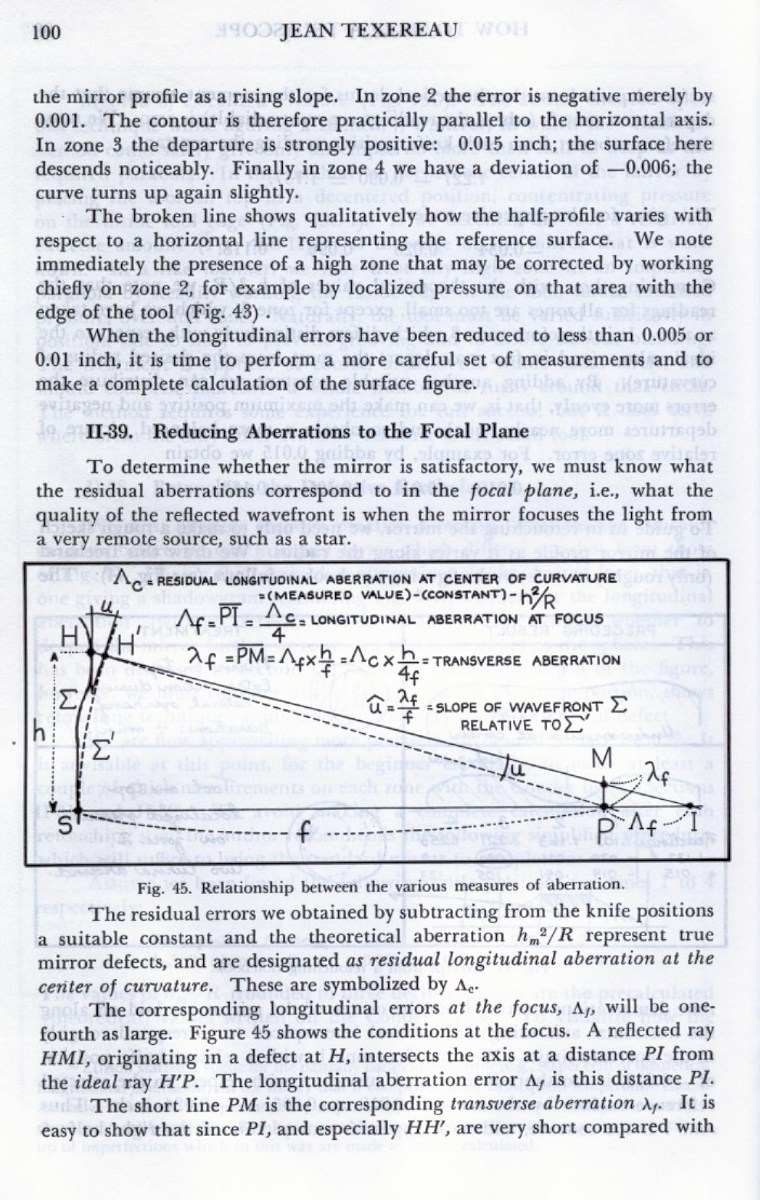
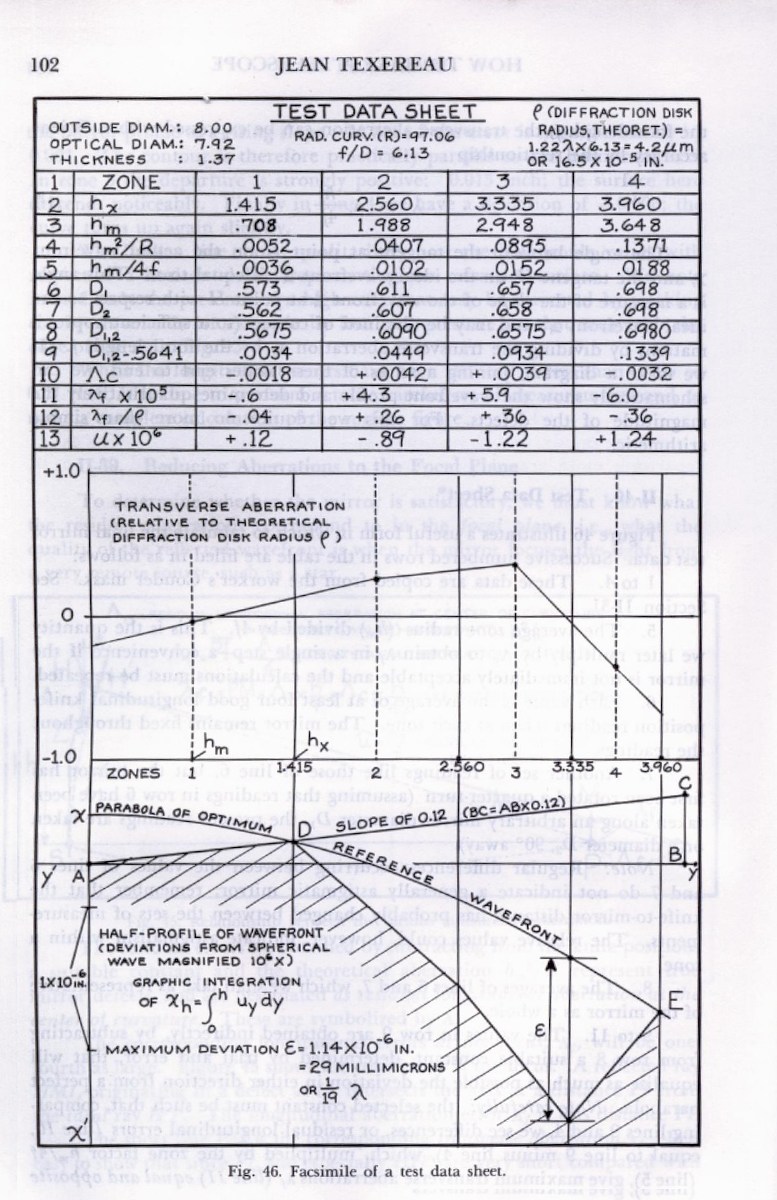
Kurt Wenske, S&W Taschenbuch 7, Spiegeloptik, 2. Auflage, Verlag S&W Düsseldorf 1978, vergriffen


E010 Parabel-Kompensation über Kugelspiegel oder Sphäre
Kompensation durch Linse oder gegen Sphäre
Ein wunderbares Spiegelschleif-Ergebnis!
Es begann damit, daß ein Spiegeldurchmesser von 210 mm zwar gegen einen Planspiegel mit 80 mm Bohrung
geprüft werden kann, von der Spiegelmitte aber nicht mehr viel zu sehen ist. Es könnte hinter der Bohrung in
der Mitte ein "Zuckerhut"ebenso versteckt sein, wie eine deutliche Mulde, die dann nur zum Teil vom ellipt.
Fangspiegel verdeckt werden würde. In einem solchen Fall bieten sich eine Plankonvex-Linse oder ein Kugel-
spiegel als Kompensations-Möglichkeit an, weil bei einem Null-Test die Fläche über ein Interferogramm, den
Roucault- und Ronchigitter-Test als Gesamtfläche eingeschätzt werden kann. Auch der Test gegen einen
Kugelspiegel (Sphäre) ist möglich. In diesem Fall steht jedoch die Lichtquelle bzw. der BathInterferometer
im Strahlengang zwischen den Spiegeln und verdeckt ähnlich wie bei der Autokollimations-Anordnung einen
zentralen Teil in der Mitte. Man vermeidet in diesem Fall aber das sekundäre Spektrum der Plankonvexlinse,
braucht aber weitere Hilfmittel, um an den Fokus des Prüfaufbaues zum kommen.
Siehe auch http://rohr.aiax.de/dall-0.jpg, http://rohr.aiax.de/hubble09.jpg, http://rohr.aiax.de/hubble09a.jpg
Die Kompensationsrechnung war über ZEMAX bereits vorbereitet und mußte nach einem exakten Vermessen vom Radius
nur noch aktualisiert werden. Das Spotdiagramm hat in diesem Fall einen geometrischen Durchmesser von 0.1 Mikron
und der Strehl liegt nahezu bei 1. Dem Datenblatt kann man den Testaufbau entnehmen. Die Restfehler, die über diesen
Testaufbau eingeführt werden, sind also verschwindend gering.

Der Spiegel selbst war noch unbelegt, was aber kein Problem ist, wenn nicht gerade die Rückseite blank poliert wäre.
In diesem Fall hätte man es mit Fremdlicht zu tun, was das Interferogramm empfindlich stören kann. So steht einer
wie immer gearteten Kompensations-Messung nichts im Wege. Würde man hingegen einen Planspiegel benutzen, dann
käme auch ganz wenig Licht wieder zurück, weil das Lichtbündel den unbelegten Spiegel zweimal passiert.

Ein ganz wichtiger Test zu Beginn ist der TEst auf Rotations-Symmetrie, eigentlich ein Ausschlußtest für Astigmatismus.
Da ja auch über den Meßaufbau bzw. der Spiegellagerung Astigmatismus eingeführt wird, kann man im Vorfeld klären,
ob in RoC ein signifikanter Astigmatismus vorhanden ist, den man berücksichtigen muß, oder ob man den Astigmatismus
vernachlässigen kann, nachdem man am Himmel selbst einen L/3 PV Astigmatismus kaum wahrnimmt. Im konreten Fall
kann man also den Astigmatismus vernachlässigen und deswegen abziehen.

Mit einer 210 mm Durchmesser Plankonvex-Linse ist eine Form der Kompensation möglich. Das Sekundäre Spektrum der
Linse selbst muß man mit einem engen Interferenzfilter auf 550 nm eingrenzen, was sich über den Solar Continuum Filter
von Baader sehr gut lösen läßt.

Verfolgt man hingegen die Compensation über einen Kugelspiegel, dann hat man das Farbproblem nicht, dafür steht aber
der Bath-Interferometer im Strahlengang und verdeckt einen Teil der Spiegelfläche, wie man auf dem entsprechenden
Interferogramm (übernächstes Bild) erkennt. Das Kompensationsprinzip bleibt gleich: Lichtquelle-Sphäre-Parabel-
Sphäre-Messerschneide. Um an das Testbild zu gelangen, genügt ein kleines Keplerfernrohr, umgekehrt verwendet und
da mit niedriger Verkleinerung. Über die Optikrechnung bekommt man auch den jeweiligen Bündeldurchmesser, wenn man
in der Bildebene eine Dummy-Blende einführt.

Im IGramm erkennbar der Haltestift und den Bath-Interferometer. Das Interferogramm stammt aus einer Kompensation
Kugelspiegel/Radius 2368 mm gegen einen 300/1500 Newtonspiegel.

Im folgenden Beispiel wurde die bereits oben gezeigte Plankonvex.Linse verwendet.

Massimo Ricardi hat auf meinen Wunsch hin in AtmosFringe eine ganz entscheidende Neuerung eingefügt. Bei der
Beurteilung der Streifenbilder besonders derer aus dem RoC (Krümmungsmittelpunkt) hat man das Problem, wie man den
Verlauf der Streifen interpretieren soll. Für diesen Fall ist eine Bezugslinie oder das ideale Interferogramm sehr wertvoll,
weil man den IST-Stand mit dem Soll-Stand vergleichen kann. Man kann mit diesem Hilfmittel klar erkennen, an welcher
Stelle der Spiegel retouchiert werden muß: Weichen die IST-Streifen nach oben ab, muß genau an diesen Stellen
noch Glas wegretouchiert werden, den nach unten abweichenden Bereich läßt man möglichst in Ruhe.

Da die Justage der Testanordnung mit einem Laser sehr schnell und unkompliziert verläuft, hatten wir sofort ein
auswertbares Interferogramm, mit einem sehr ansprechenden Ergebnis.

Auch über den RoC Gegenbeweis entstand nahezu das gleiche Strehlergebnis.


Bei der Kompensation mit einer Linse sind der Foucault- und der Ronchi-Gitter-Test ebenfalls möglich, solange man einen
engen Interferenzfilter verwendet. Beide Tests zeigen, mit wieviel Sachverstand und Liebe der Sternfreund seinen
Spiegelgeschliffen hat. Ein Umstand den ich nur positiv würdigen kann.

Die schnurgeraden Ronchi-Linien haben mich besonders begeistert. Ich habe aus meiner Anerkennung kein
Hehl gemacht.

Weitere Bilder zur Kompensation gegen Sphäre

Fringe Map between the mirrors

Die Einheit Bath-Interferometer

Das gesamte Bauteil

Der Spiegel under test

Die Kompensations-Sphäre

###################################################################################
this Waineo-Test would work. This is just the setup in ZEMAX. Later I try to calculate your system.
This test is a one-way-test, and you just can test with Ronchi and Foucault as null test.

##################################################################################
Dear Franck,
you hole in the sphere is to small. I should be 50 mm and more. Now I insert values similar as yours. If the
hole is to small, the distance mirror-focus must be small for the 30 mm sphere hole, but for this the sphere
diameter must be larger. But if the whole is bigger, better 50 mm, so the sphere diameter becomes smaller.

a second example with the values of your program waineo2006.zip

calculated with ZEMAX:

##################################################################################
Dear Franck,
Waineo: with 150 mm distance from the sphere surface the focus is very closed to handle any test, but it is possible.
Now the setup with your sphere 2535 and the parabola 400 R 4000: If you use an ellipt. flat, you have an
alligne problem, be sure. But her this could be the solution: http://rohr.aiax.de/ParabelSphere02.jpg
In that case the flat should be as small as possible about 30 mm, because the light cone at that position
is about 198 mm in diameter, and so you need about 100 mm outside the light cone and more. Good luck!

E044 Elliptische Flats - Planspiegel testen
elliptische Planspiegel testen
siehe auch: http://r2.astro-foren.com/index.php/de/13-beitraege/05-messtechnik-teil-1/50-flat-10-inch-pruefen
und: http://r2.astro-foren.com/index.php/de/14-beitraege/06-messtechnik-teil-2-aufbau-diverser-interferometer/698-f044a-artificial-sky-test-bei-zwei-refraktoren
Elliptische Planspiegel kann man entweder auf Kontakt gegen eine Referenz-Fläche prüfen, dann sollte der Flat aber unbelegt sein, damit ein
kontrastreiches IGramm entsteht. Bei einem beschichteten Spiegel, besonders bei dielektrisch-beschichteten Spiegel, ist ein Interferogramm
zwischen der unbeschichteten Referenzfläche und dem Flat kaum noch erkennbar.
Ein weiteres Problem bei der Prüfung auf Kontakt ist die elliptische Fläche selbst, da die gängigen Auswert-Programme nur "runde" IGramme
auswerten können. Man könnte sich in diesem Fall entweder dadurch behelfen, indem man die lange Achse auf die kleine Achse im Computer
verkürzt - auch dann hätte man ein rundes IGramm. (Im Strahlengang bei 45° Kippwinkel würde man ohnehin einen Kreis sehen)
Einfacher wäre für elliptische Planspiegel ein Test, der der Funktion des Flats im Strahlengang möglichst nahe kommt. Dieser Test ist u.a.
im dreibändigen "Amateur Teleskop Making" beschrieben. (Band one S 42f und S 242f, und im Übrigen George Willis Ritchey zugeordnet
wird.) Ein Flat läßt sich (wie im Band one ausführlich beschrieben) entweder gegen eine Sphäre prüfen, gegen eine Wasser-Oberfläche oder
mit Hilfe einen guten Refraktors. Im Falle der elliptischen Flats empfiehlt sich die Prüfung gegen eine Sphäre. Für diesen Fall bekommt man
ein rundes Interferogramm mit doppelter Genauigkeit, das sich leicht von einem Programm auswerten läßt.
Um aber zu keinem "verstiegenen" Disput anzuregen mit in der Regel praxis-fernen Argumenten, zunächst das Datenblatt von ellipt. Flats,
die von Pörschke bzw. Edmund Scientific als Labor-Qualität zu beziehen sind. Mit einer Oberflächen-Qualität von PV L/8, was einer Wellen-
front-Abweichung von PV L/4 entspricht, liegt man in genau der Toleranz, die für elliptische Flats ausreichend sind, was ich an anderer
Stelle bereits nachgewiesen habe.
In der Regel sind kleinere Flats "genauer" als die größeren Durchmesser, die bei einem Durchmesser von 100 mm kleine Achse dann ca.
1 Kilo-Euro kosten können.
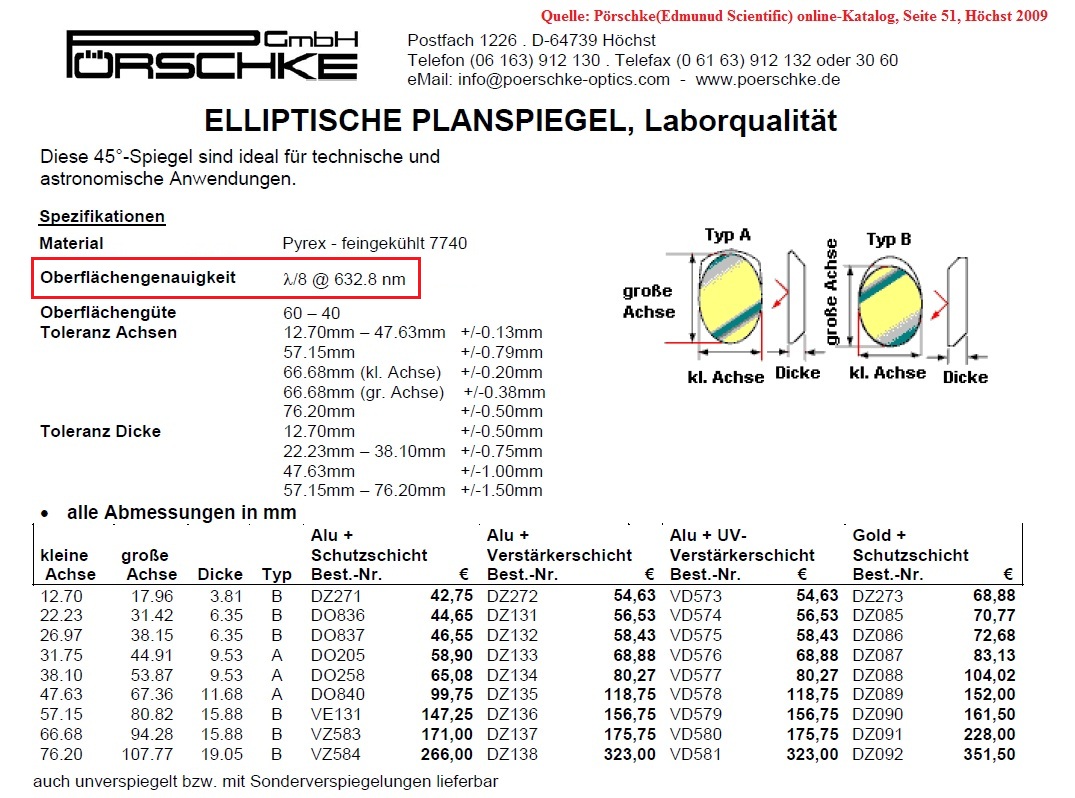
Das Prinzip des Testaufbaus ist einfach: In den konischen Strahlengang wird der Flat genauso in den Strahlengang gestellt, wie er bei einem Newton-Teleskop
auch stehen würde. Da man jedoch die ganze Fläche des Plan-Spiegels messen möchte, rückt dieser entsprechend nahe an die Sphäre. Der Lichtkegel der
Sphäre, aus dem Krümmungsmittelpunkt betrachtet, wird als um 90° umgelenkt. Das Lichtbündel passiert die Planfläche zweimal. Bei einem Durchmesser der
Sphäre von ca. 150 mm bei einem Krümmungsradius von ca. 600 mm hat man also eine kurze Strecke, die wenig Störungen verursacht. Je kleiner der Flat
ist, umso weniger Referenzfläche der Sphäre wird benutzt, und das Ergebnis wird entsprechend genauer.
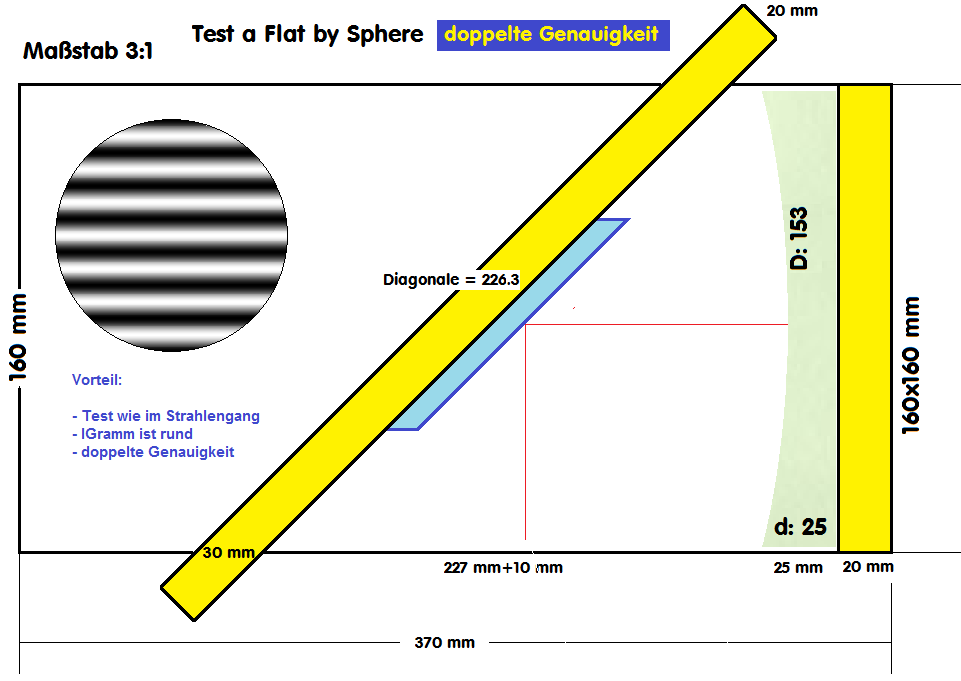
Koma wird man in jedem Fall abziehen können, das Hauptproblem bei Flats ist Astigmatismus, der direkt dem Flat zugeordnet werden kann, aber auch über die
Power entsteht, wenn auf dem Flat ein "Radius" eingeschliffen ist.

Beim Einrichten des Testaufbaus sollte der Flat mittig sein, was man über ein Maßband vom Rand der Sphäre leicht einstellen kann. Daß die opt. Komponenten
spannungsfrei gelagert werden müssen, ist eine Selbstverständlichkeit.

Der gleiche Testaufbau, nur von oben gesehen.

Nun der Vergleich zweier Testverfahren:
Links die Prüfung auf Kontakt, die sich schwer in PV- und Strehl-Werten darstellen läßt. Rechts ein IGramm aus der beschriebenen Testanordnung. Die Werte liegen
unterhalb der oberen Labor-Qualität.

Bei größeren Durchmessern sinkt die Qualität, in diesem Fall ein deutlicher Astigmatismus, der über das Kontakt-Verfahren weniger
deutlich erkennbar ist.

Anzumerken ist, daß eher selten die gesamte Fläche eines ellipt. Flats benutzt wird, während sich aber die Auswertung auf die gesamte
Fläche des Interferogrammes bezieht und damit auf den vollen Durchmesser. Schon wegen der Vignettierung wird man immer einen
etwas größeren ellipt. Flat benutzen. Fangspiegel-Qualität bei einem Newton
der "unbekannte" Fangspiegel - Messung gegen eine Sphäre bei 90° Verkippung
###############################################################################################
70 mm elliptischen Flat prüfen a) doppelter Durchgang gegen Sphäre b) einfacher Durchgang mit TSA 120/900
Ein und derselbe 70 mm Flat wurde auf zweierlei Verfahren geprüft, a) im doppelten Durchgang gegen eine Sphäre, wie oben bereits
vorgestellt, und b) im einfachen Durchgang durch ein TSA-Objektiv 120/900.
Der Testaufbau im doppelten Durchgang gegen eine Sphäre im Winkel von 45° erzeugt ein rundes Interferogramm, das leicht
auszuwerten ist. Dieser Testaufbau entspricht der Position des Planspiegels im Newton-Strahlengang - ein Radius auf der
Planfläche des Flat's würde zusätzlich als Astigmatismus erkennbar sein.
a) doppelter Durchgang gegen Sphäre

Der Testaufbau, wie bereits beschrieben und in der Zeichnung dargestellt.

Der Artificial Sky Test ist ein abgewandelter Star Test, dessen Pinholes zwischen 3 - 5 Mikron im Durchmesser sind. Verformungen zeigen deshalb sehr
genau die optischen Fehler des geprüften Flats an, exakt so, wie man das am Himmel auch sehen würde.

Wegen der 45° Position des ellipt. Flats entsteht ein rundes IGramm, das sich leicht auswerten läßt und zudem den Vorteil der doppelten Genauigkeit
hat. Man erkennt bereits den Fehler an der Verformung der Streifen.
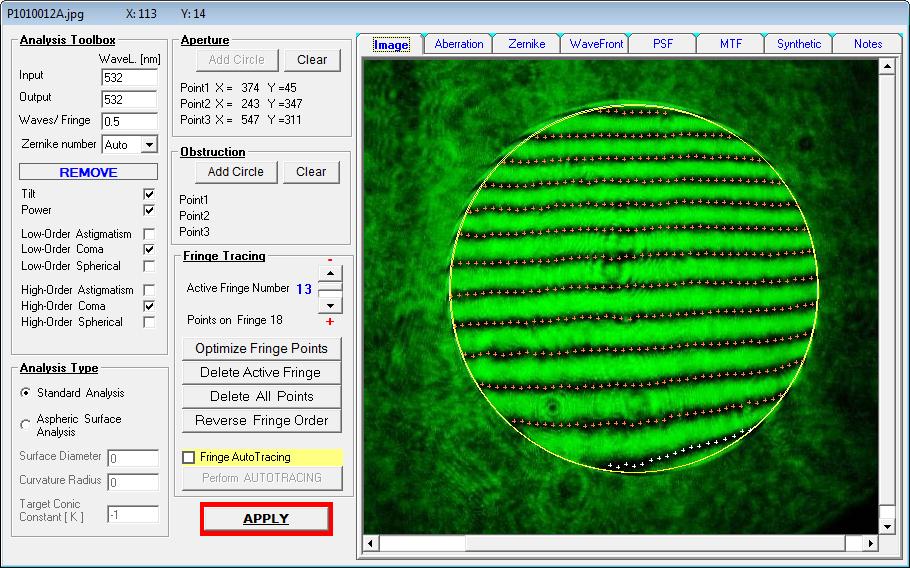
Über die Wellenfront-Deformation läßt sich Astigmatismus als Hauptfehler zeigen
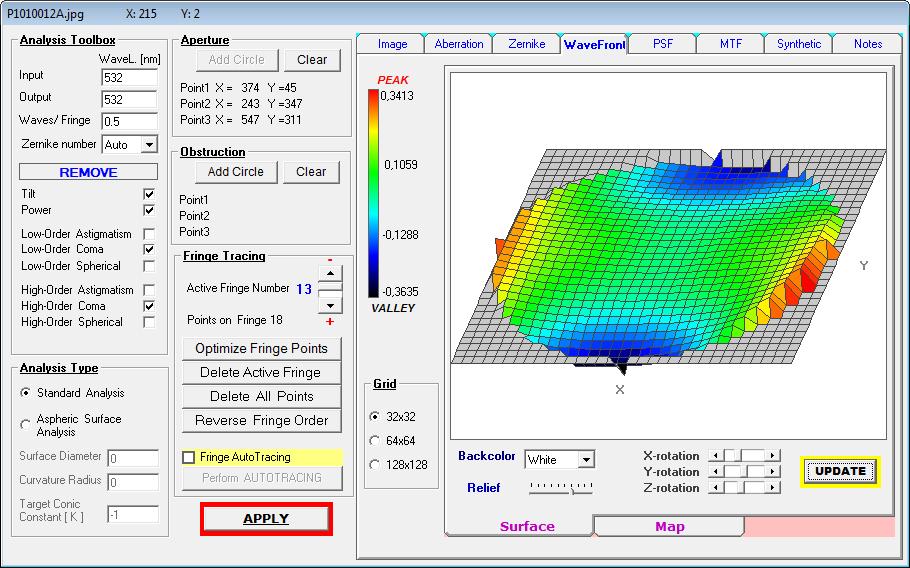
. . . der in seiner Größe von PV L/1.4 der Wellenfront nicht die Vorgaben z.B. von Edmund Scientific erfüllen würde. http://rohr.aiax.de/@FS_15.jpg
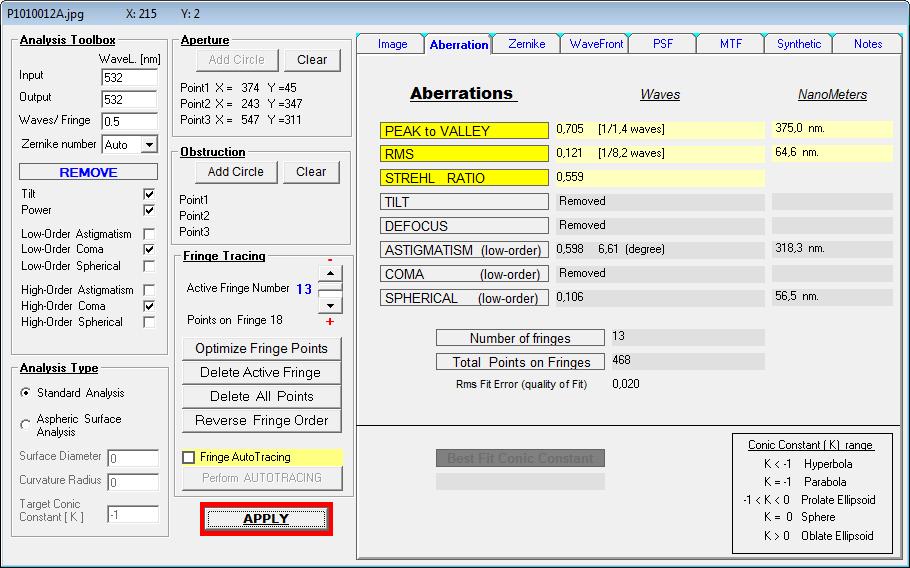
b) einfacher Durchgang durch TSA 120/900
Beim einfachen Durchgang wird in einer Autokollimations-Anordnung nicht der Refraktor getestet, sondern der elliptische Planspiegel. Gegen den
Zeiss Werkstatt Spiegels wird der ellipt. Flat getauscht, sodaß deshalb ein ellipt. Interferogramm entsteht. Der Referenz-TSA muß deshalb auch
hinreichend genau sein, also etwa in der Gegend von PV L/10 der Wellenfront. Der ellipt. Flat wird also in diesem Setup mit einfacher Genauigkeit
geprüft, was jedoch nicht ganz der Situation am Himmel entspricht, weil über die 45° Stellung des Planspiegels im Newton-System die X-Achse
"gestaucht" wird und damit die Unterschiede erklärt beim Artificial Sky Test. In beiden Fällen erkennt man aber den Astigmatismus.
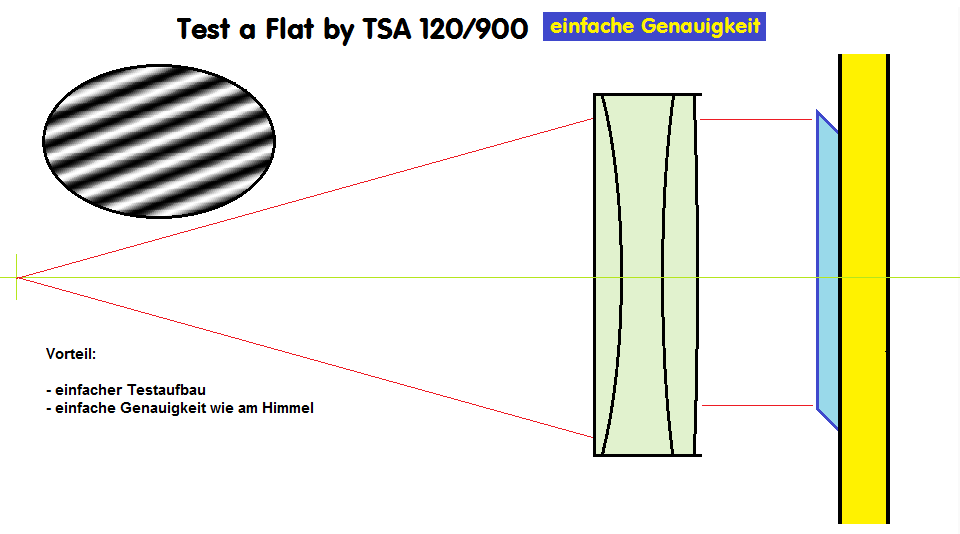
Der Testaufbau im Foto

Und zunächst der Test gegen den Zeiss Werkstatt Spiegel, als Referenz, wie das optimale Prüfergebnis des 70 mm ellipt. Flats eigentlich aussehen sollte.

Mit diesem Bild ist eindeutig, daß derselbe 70 mm ell. Flat auch im einfachen Durchgang Astigmatismus als Fehler anzeigt - nur ist in diesem Testaufbau
die X-Achse nicht verkürzt, weshalb die Situation des Planspiegels nicht ganz exakt wiedergegeben wird: Während im einfachen Durchgang eine eher
regelmäßige Figur entsteht, verkürzt sich über die 45° Stellung die "Spot-Figur" und wird damit dem Artificial Sky Test oben ähnlicher.

Aber auch das IGramm zeigt Ähnlichkeiten mit dem IGramm aus dem oberen Testaufbau, betrachtet man die Streifen etwas genauer. Weil aber
das IGramm eine ovale/elliptische Form hat, ist die übliche Auswertung etwas schwieriger. Man muß also erst die X-Achse so verkürzen, daß
wieder ein kreisförmiges IGramm entsteht. Damit sollte der Test eines ellipt. Flats im einfachen Durchgang genau genug sein, wenn man
eine entsprechend klein dimensionierte Pinhole (5 Mikron) verwendet. Man muß allerdings genau hinschauen.

Durch Stauchung der X-Achse erhält man ebenfalls ein rundes Interferogramm, das in ähnlicher Form den Fehler zeigt. Nun ist der
Scale aber nur 1, im doppelten Durchgang wäre er 0.5. Die beiden Strehl-Ergebnisse stimmen zwar nicht hundert-prozentig überein,
aber auch die Wellenfront-Darstellung zeigt exakt den gleichen Fehler. Insgesamt erscheint der Doppelpaß-Testaufbau realistischer
zu sein.
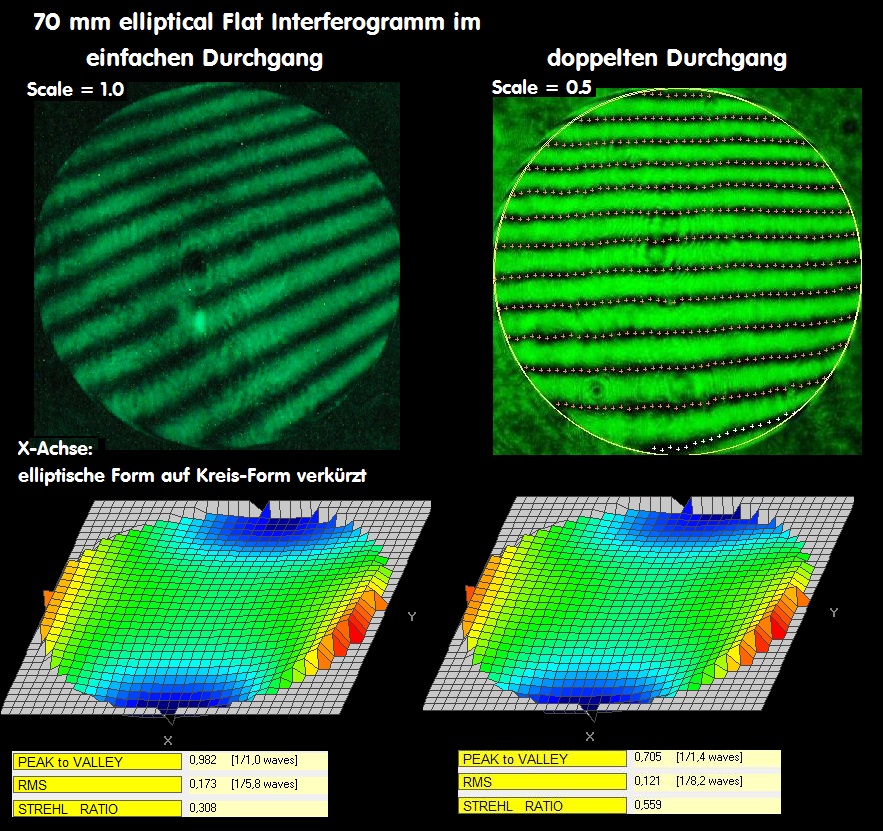
. . . . .
############################################################################################
sechs weitere Planspiegel im Test
Die Qualität von Fangspiegels scheint in der Praxis doch nicht so kritisch zu sein - wenn man sich die Erfahrungen von Händlern vergegenwärtigt.
Mithin ein Grund, über diesen Sachverhalt ein weiteres Mal zu berichten.
Zunächst muß man sehr deutlich unterscheiden zwischen Fangspiegeln, die bei der Feldfotografie eingesetzt werden und solchen für visuelle
Nutzung. Anspruchsvoller ist die zweite Variante. Wieviel der im Foto gezeigten jeweiligen Fangspiegel-Fläche wird denn optisch zur Abbildung eines
Punktes überhaupt gebraucht? Und immer nur genau diese Fläche muß einer Qualitäts-Norm von mindestens PV L/4 wave oder PV L/8 surface ent-
sprechen. Das gilt gleichermaßen für die Abbildung auf der opt. Achse, wie für die Sternabbildung im Bildfeld.
An folgendem Beispiel mag dies ersichtlich werden. Bei einem 10" Newtonspiegel f/5 (250/1250) ist bei 1 Meter vom Spiegel entfernt der Fangspiegel
plaziert, sodaß der Fokus mit 250 mm Abstand von der opt. Achse bequem außerhalb des Tubus zu liegen kommt und somit auch noch ein Koma-
Korrektor eingesetzt werden kann. (Dieses Beispiel fixiert nur eine bestimmte Situation und kann entsprechend variiert werden.)

Diese Situation wurde maßstäblich so dargestellt, daß 1 Pixel 1 Millimenter entspricht. Im f/5 Lichtkegel, den dieser Spiegel erzeugt, haben wir bei einem Abstand von
1000 mm vom Newton-Spiegel einen Kegel-Durchmesser von 50 mm, was zur Abbildung eine Sterns auf der opt. Achse völlig ausreichend wäre. Im Bildfeld jedoch
hätten wir schnell die bekannte Vignettierung, die mit Helligkeitsabfall einhergeht. Der Fangspiegel am Ort 1000 mm muß also im Durchmesser größer sein als 50 mm.
Man muß also zunächst das gewünschte Bildfeld im Fokus selbst festlegen. In Anlehnung an das Kleinbildformat 24x36 mm ergäbe sich ein Bildfelddurchmesser
(Diagonale) von ca. 43.26 mm. Zugunsten einer einfacheren Rechnung nehme ich 40 mm als Bildfelddurchmesser.
Damit entsteht ein umgekehrter Kegel vom Fokus-Bildfeld-Durchmesser bis zur Mitte des Newton-Spiegels, der in der Höhe des Fangspiegels nur noch 32 mm Durch-
messer hat. Dieser Betrag muß also zu den 50 mm dazugezählt werden und man bekommt 82 mm Fangspiegel kleine Achse für die Position 1000 Abstand vom HS.
Damit läßt sich vignettierungsfrei das Bildfeld 40 mm im Fokus des 10" f/5 Newton ausleuchten.
Unabhängig davon braucht man für die Abbildung eines einzelnen Stern, wo immer er im Bildfeld ist, weiterhin den Fangspiegeldurchmesser von 50 mm.
Ein Prüf-Protokoll würde sich aber nun auf die Gesamtfläche des 82 mm Fangspiegels beziehen und gibt daher keinerlei Auskunft, wie tauglich dieser Spiegel in einem
bestimmten System überhaupt ist.
.
Diese Frage kann man nun auf mehrere Art beantworten:
Mit Hilfe des Artificial Sky Testes (siehe die Berichte weiter oben) kann man in die Abbildung bei Höchstvergrößerung untersuchen und zwar a) über den vollen Durchmesser des
Fangspiegels und b) dem tatsächlich benutzen Durchmesser über die Einführung einer Blende. Bei der Auswertung der Interferogramme kann man ebenfalls a) den vollen Durch-
messer und b) einen prozentual verkleinerten Durchmesser auswerten, wobei ich hier von 80% des Gesamtdurchmessers ausgegangen bin, was bereits zu einer erheblichen
Qualitäts-Steigerung führt. Der Artificial Sky Test zeigt sofort einen vorhandenen Astigmatismus, der ein Hinweis auf fehlende Planität darstellt bzw. die Power. Bei mittlerer
Vergrößerung wird man diesen Sachverhalt eher schwer feststellen können.
Da dieser Test abhängig ist vom Radius 600 mm des Kugelspiegels ist, sind die Sternscheibchen-Durchmesser bei einem kleinen Spiegeldurchmesser entsprechend größer nach der
Formel: Auflösung (550 nm) = 138.40/D. Man muß also auch noch den Durchmessers des Fangspiegels berücksichtigen beim Betrachten der Testbilder.
.
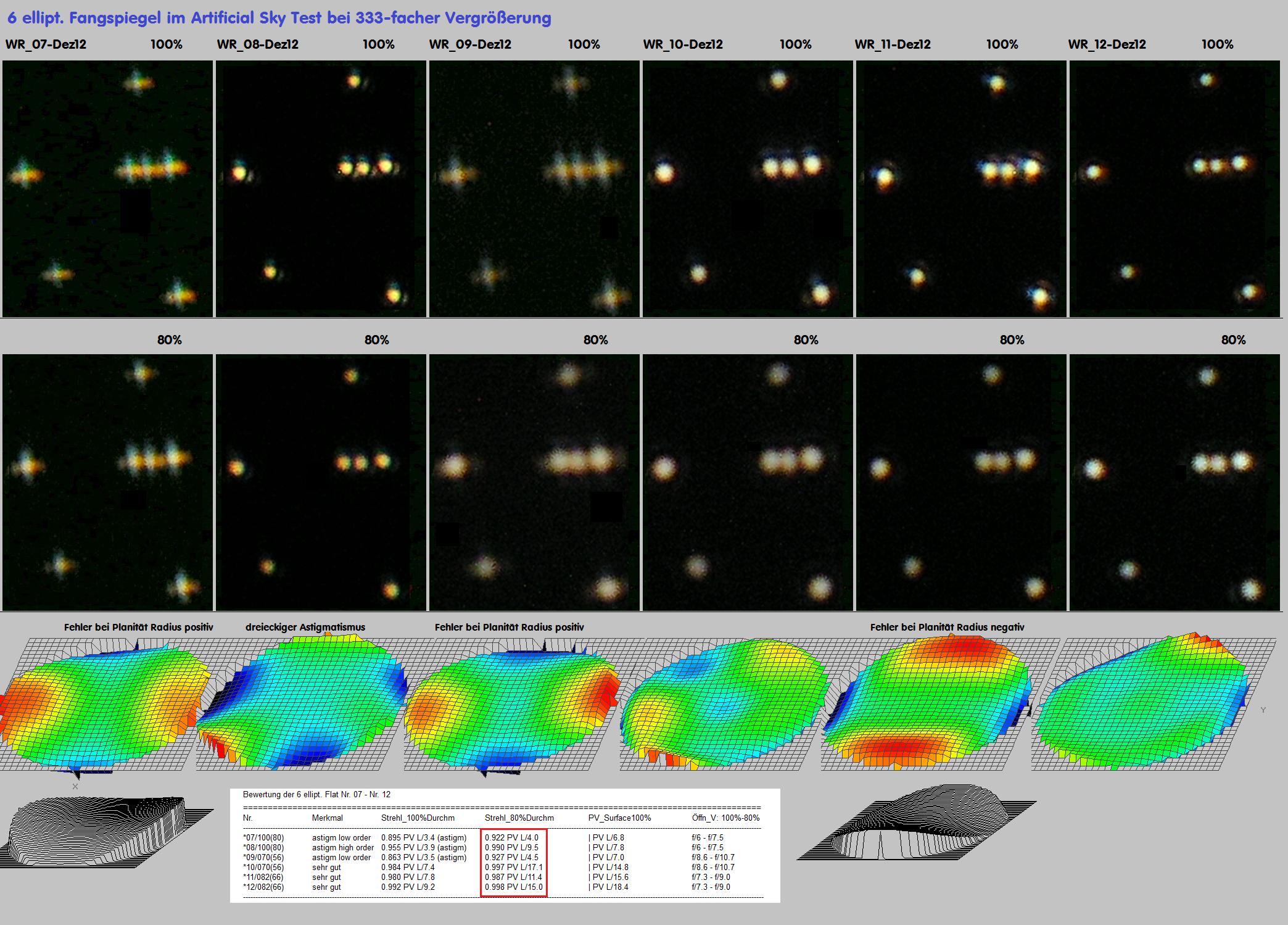
Spiegel Nr. 7, 9 und 11 erzeugt ein großer Radius auf der Planfläche einen Astigmatismus der Grundordnung - bei 7 und 9 wäre es ein positiver Radius, bei Nr. 11 ein negativer Radius. Auch die Strehl und PV-Übersicht zeigt deutlich, wie schnell die Flächenqualität zu nimmt, je kleiner die benutzte Fläche des Fangspiegels ist.
Im nächsten Bild sind die Ergebnisse von 100% Nenndurchmesser zu 80% Nenndurchmesser dargestellt. Der Umkreis von 100% wurde auf 80% reduziert, was nur noch 61% vom
Gesamtdurchmesser entspricht bzw. 50 mm. Auf die Fläche umgerechnet reduziert sich die Gesamtfläche auf nur noch 37% der Gesamtfläche, die man in diesem System tatsächlich
für die Abbildung eines Sternes braucht. Nun so ist es zu erklären, warum Fangspiegel von mittelmäßiger Qualität sich im praktischen Gebrauch sehr unauffällig zeigen.
.
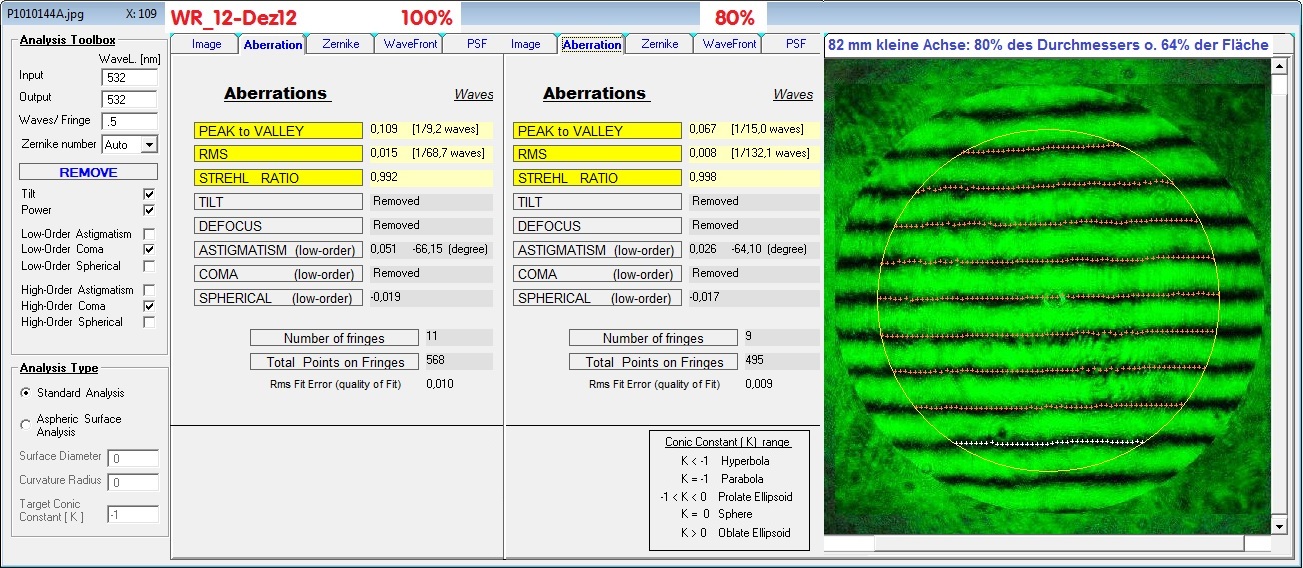
.
.
.
E045 elliptischer Planspiegel (Fangspiegel) 170 mm kleine Achse Test gegen Sphäre-Kugel
7. Oktober 2012
Newton-System: elliptischer Planspiegel (Fangspiegel) u. C013 elliptical flats ~.de>Link
Vasco Ronchi, bekannt seit 1923 durch den Ronchi-Test, soll ebenfalls Planspiegel gegen einen Kugelspiegel (Sphäre) geprüft haben,
wie der Testaufbau im übernächsten Bild zeigt. Einen solchen Fangspiegel mit 170 mm kleine Achse hatte ich hier auf Tauglichkeit
zu prüfen. Dazu gibt es u.a. auch diesen Link: http://www.reinervogel.net/index_e.html?/lowrider/plan_e.html
Warum also der Hersteller dieses ellipt. Planspiegels diesen doch bekannten Test nicht ebenfalls kennt, und vor allem benutzt, läßt
sich leider nicht ermitteln. Er reagierte nur etwas verschnupft auf meine Testergebnisse - soll mir egal sein !
Siehe auch: http://rohr.aiax.de/AN510-Ritchey_04233.pdf
Hier liegt also das gute Stück, dessen Preis um den Faktor 4 steigt, wenn ihn LOMO hergestellt hätte, dann hätte ich ihn aber vermutlich auch nicht
testen müssen. Ein gleichgroßer Fangspiegel eines anderen Herstellers war völlig unbrauchbar bei diesem Test - der Glaskörper hatte sich bei der
Beschichtung möglicherweise verzogen - der Wahrheitsbeweis kann nicht geführt werden.

Der Referenz-Kugelspiegel sollte im Bereich von PV L/10 der Wellenfront liegen, wobei bei diesem Test vor allem der Astigmatismus entscheidend ist.
Wenn nämlich ein Planspiegel nicht ganz plan ist und auf der Fläche in Wirklichkeit ein Radius einpoliert worden ist - auch wenn es mehrere Kilometer
wären - dann entsteht über die perspektivische Verkürzung der senkrechten Achse ein Astigmatismus, der umso größer wird, je flacher man über die
Fläche "schaut". Bei einem Newton-System ist der Kippwinkel des Spiegels 45°, der den Strahlengang um 90° umlenkt. Genau unter diesen Bedingungen
kann man also den Flat testen, ob er auch wirklich plan ist. Genau dann erzeugt dieses opt. Bauteil keinen Astigmatismus.
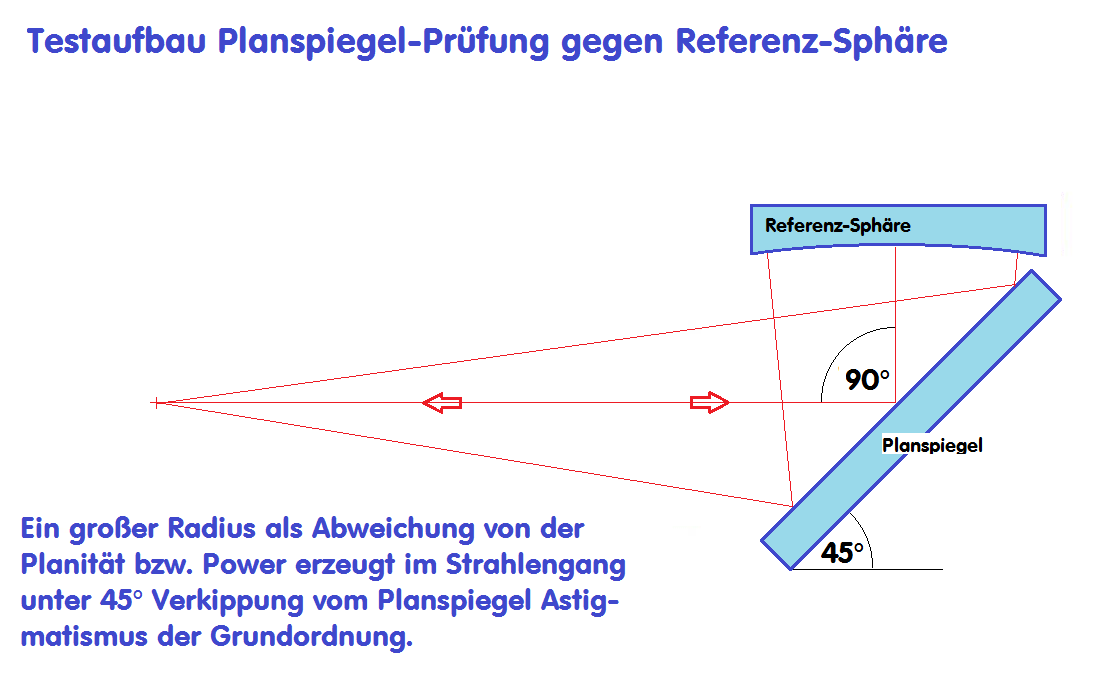
Kugelspiegel
Die erste Aufmerksamkeit gilt dem Kugelspiegel als Referenz-Spiegel mit Durchmesser 250 R 2368 mm. Als Referenz-Spiegel sollte der mindestens PV L/20 der
Oberfläche haben, in jedem Fall bezogen auf den Astigmatismus. Aus diesem Grund wurden eine Reihe ganz unterschiedliche Tests mit diesem Spiegel gemacht.

Mit dem Scatter Plate Interferometer exakt auf der opt. Achse entstand bei 405 nm wave (violettes Laser-Modul) dieses Interferogramm.
.

Der PV-Wert der Wellenfront für den Rest-Astigmatismus liegt in jedem Fall unter L/10, bzw. ist visuell nicht mehr wahrnehmbar, was für den späteren
Artificial Sky Test eine Rolle spielt. http://www.astro-foren.de/showthread.php?7874-Artificial-Sky Die Auflösung dieses Testes sollte im Ideal-Fall
mit der Abbildung durch den Kugelspiegel identisch sein.
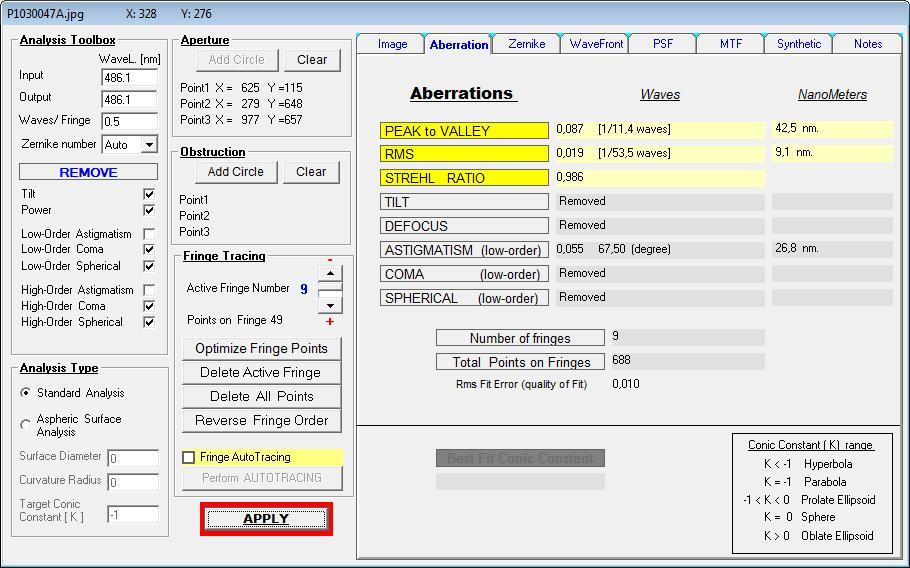
Es ist also kein quantitativer Test mit Strehl oder PV-Wert Angaben, weil für diesen Fall die Zahlen aus Vergleichsgründen nicht anschaulich genug sind.
Sehr viel anschaulicher dagegen ist ein Artificial Sky Test unter HÖchstvergrößerung von 1315-facher Vergrößerung, weil sich über eine solche Foto-
grafie sowohl die Auflösung zeigen läßt und bei einem fehlerhaften Flat auch die Abbildungsfehler - bei mangelnder Planität (Power) den Rest-
astigmatismus. Im Krümmungsmittelpunkt der Sphäre von 2368 mm entsteht also dieses Bild, dessen theoretische Auflösung sich über das Foto beweisen
läßt. Genau dieses Bild bzw. dessen Auflösung erwartet man, wenn man zuusätzlichen einen Planspiegel in den Strahlengang stellt, genau wie das bei
einem Newton-System der Fall ist.
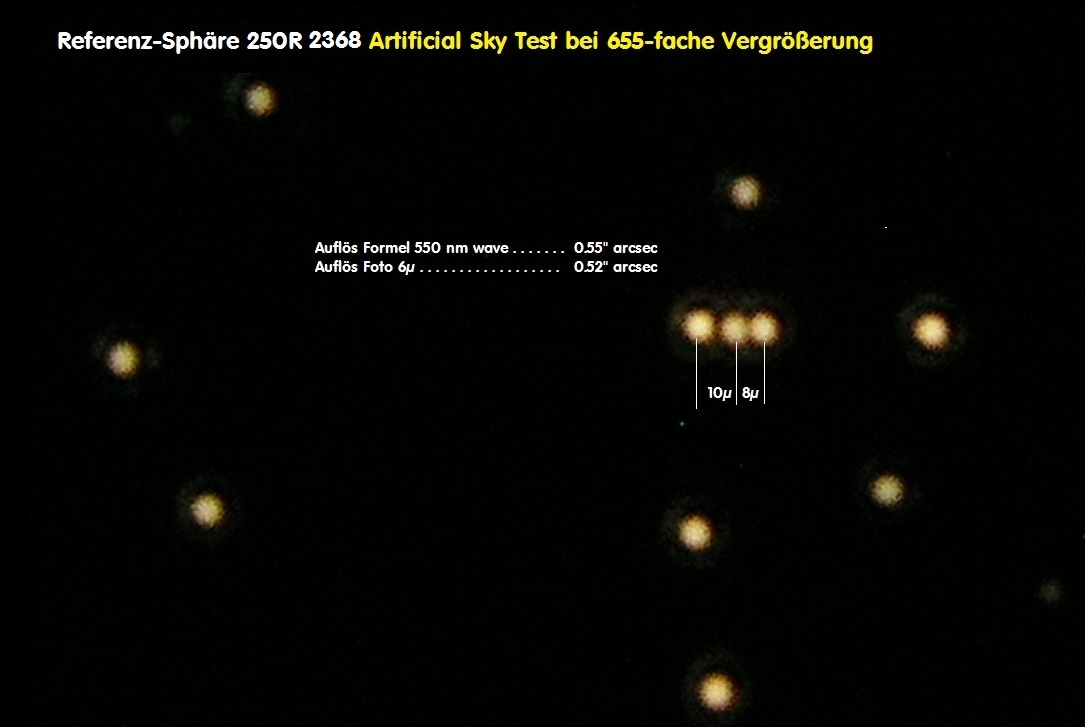
Kugelspiegel + Zeiss Planspiegel
Ein Zeiss-Werkstatt-Spiegel mit Durchmesser 210 mm war nun das erste "Opfer", um Beweis-Material zum Thema Planspiegel-Qualität in die Hände zu bekommen.
Worauf sich genau der PV-Wert von 0.033 bezieht, auf "surface" oder auf "wavefront", ist dem eingeblendeten Filmstreifen nicht zu entnehmen.
.

Davon unabhängig erfüllt dieser Planspiegel in der 45° Position zur opt. Achse die Abbildung recht gut.
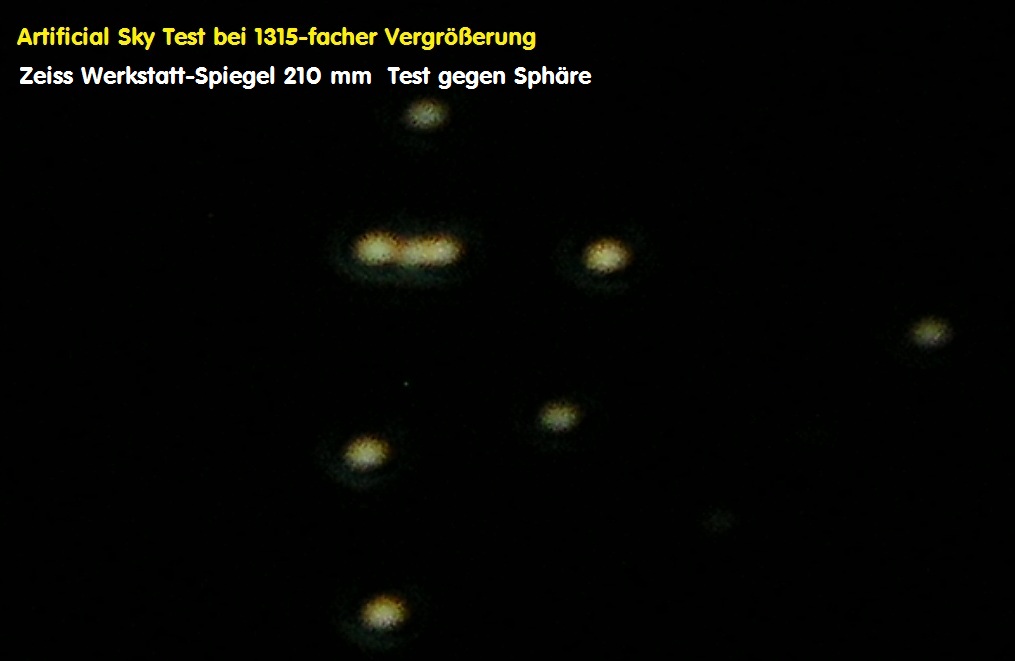
Hätte also der obere ellipt. Flat diese Abbildung abgeliefert, wäre dieser Bericht hier kaum entstanden.
Kugelspiegel + 165 mm Planplatte
Ein zweites Beispiel liefert eine unbelegte Planplatte, die 1995 vom Peter Rucks getestet worden war, mit dem sagenhaften Radius von 6 923 km - wenn's stimmt.
Und weil diese Planplatte nicht beschichtet ist, hat man mit der Helligkeit beim Artificial Sky Test seine liebe Not. Es waren 16 Sek. Belichtungszeit von Nöten, um
überhaupt eine Abbildung zu bekommen.

Hier also auch das 1995 erstellte Rucks-Zertifikat.
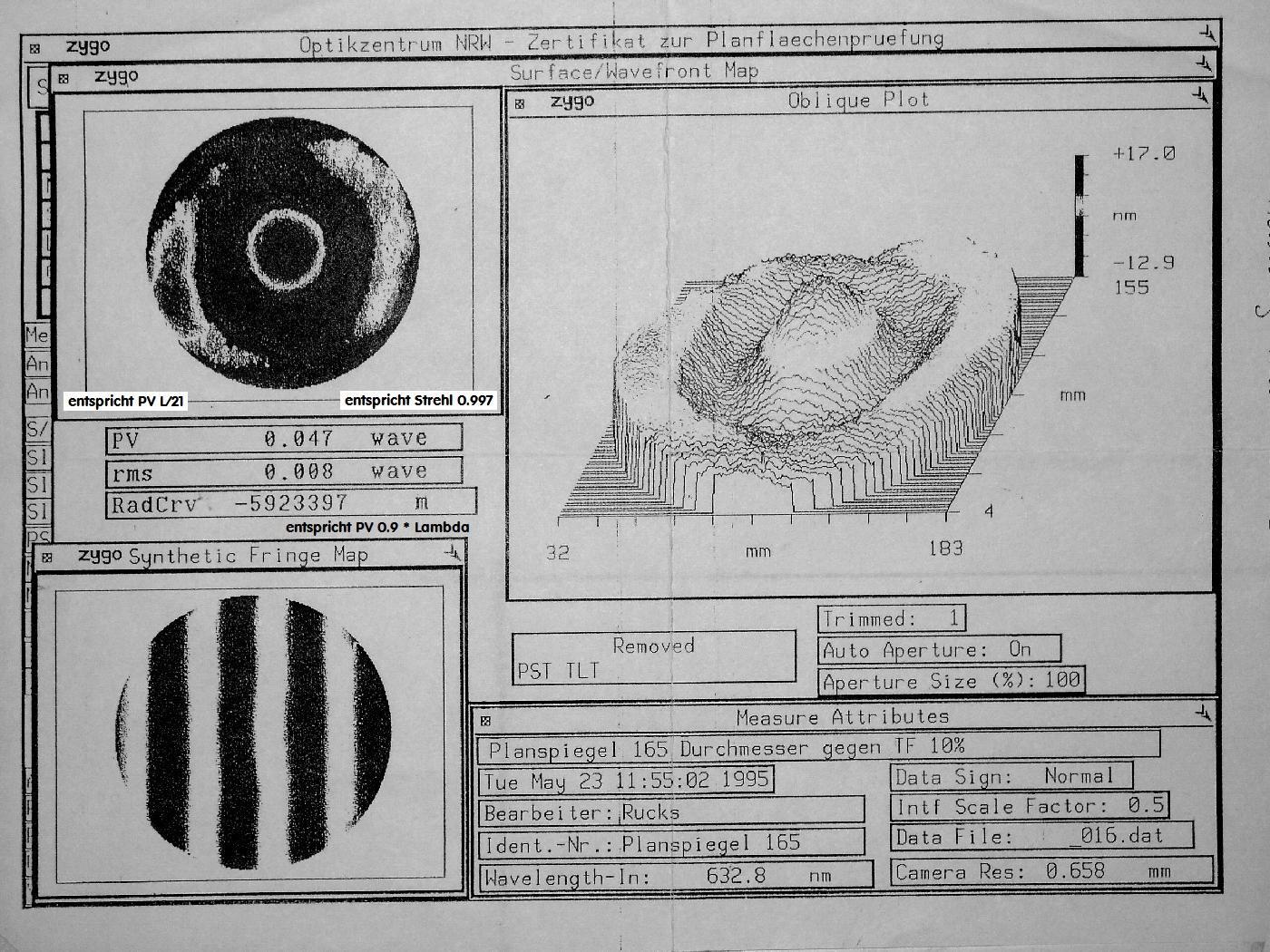
Mit diesem Planspiegel Durchmesser 165 mm entstand also das folgende Bild.

ellipt. Planspiegel 170 mm
Nach dieser Vorarbeit nun zum eigentlichen ellipt. Planspiegel 170 mm. Der Testaufbau wurde oben bereits beschrieben.

Wäre dieser Planspiegel in ähnlicher Qualität, wie die vorher beschriebenen, so müßte eine ähnliche Abbildung herauskommen -wie man sie
gerne bei einem Newton-System wünscht. Stattdessen enstehen deutliche astigmatische Figuren, die in der Streifenbild-Auswertung den
Wert PV L/2.7 annehmen.
.

Mit gleichen Testaufbau wurde also bei 532 nm wave dieses Igramm erstellt und ausgewertet: Wobei sich das Augenmerk auf den Wert für den
Rest-Astigmatismus richtet.
.
Maßgeblich wäre in diesem Zusammenhang der Astigmatismus (low) der Grundordnung, wie er bei einer Sphäre mit großem Radius über die
Verkippung entsteht. Über die Auswertung eines solches Streifenbildes bekommt man also einen Wert für den Astigmatismus, aus dessen
Größe sich bei einer Verkippung von 45° der große Krümmungsradius der Planfläche rechnen läßt: Er könnte im Bereich von 10 km und mehr
liegen. Mit Harrie Rutten bin ich augenblicklich über ZEMAX dabei, diesen Wert zu ermitteln.
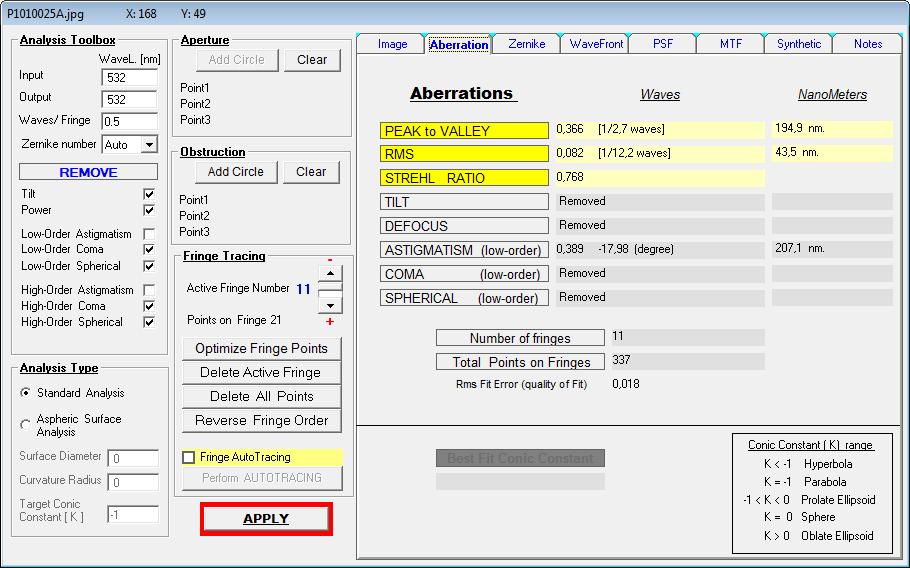
Für den Spiegel spricht natürlich der Preis und auch die Tatsache, daß von der Spiegelfläche nur. ca. 70% vom Durchmesser benutzt werden,
während bei meinen Tests immer der ganze Durchmesser gemessen wird. Mit einer Blende haben wir das simuliert. Diese reduziert den Astigmatismus
ein klein wenig.

Unbrauchbar hingegen war der erste derartige ellipt. Planspiegel eines anderen Herstellers, siehe Einleitung.

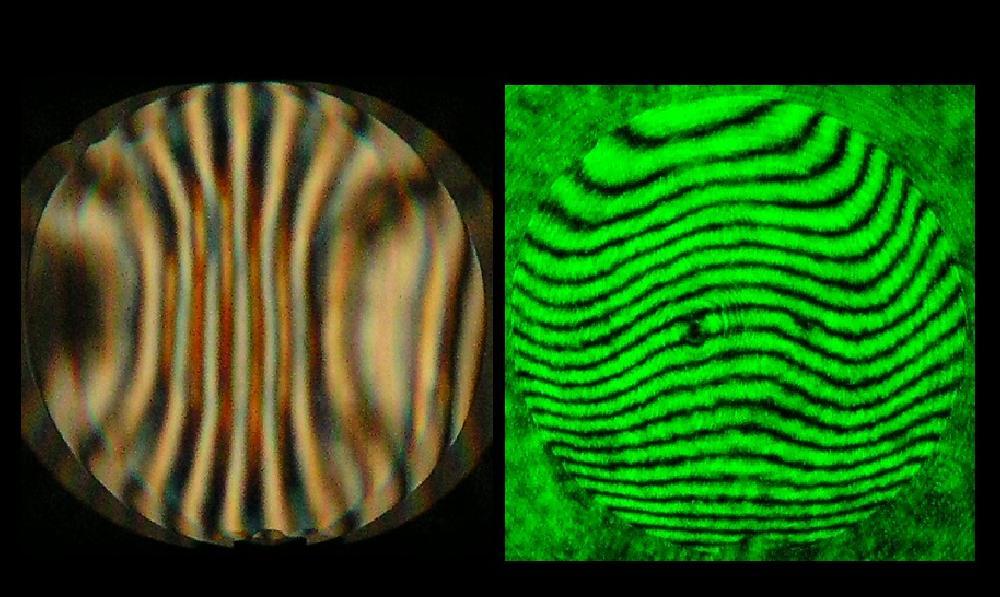

############################################################################################
Anmerkung zur Planität von Planflächen oder der "Power" von Planflächen:
Die Planität oder Power (Der Zernike Zoo) einer optischen Fläche bedeutet, daß es in Wirklichkeit keine absolute Ebene ist,
sondern in Wirklichkeit eine konkave oder konvexe Krümmung ist, bzw. eine Sphäre mit einem Radius von mehreren Kilometern.
Eine Wasseroberfläche auf der Erde mit Durchmesser z.B. 250 mm hätte dann eine Power von ca. L/500 PV surface, auch das
ist strenggenommen keine absolute Ebene, aber sehr, sehr genau. Gegen diese Wasser-Referenz-Fläche kann man also
Planspiegel testen: Der Rayleight Water Test - Messen gegen eine Wasseroberfläche
Solange bei einem optischen System, Test oder ähnlichem, das Lichtbündel senkrecht auf den Planspiegel fällt, wirkt sich die Power in keiner
Weise aus. Ein Kollimations-Spiegel muß deshalb nicht streng "plan" sein, er kann also eine Power habe, ohne daß damit das Testergebnis
überhaupt beeinflußt wird.
Ganz anders verhält es sich bei einem Newton-System, bei dem der Planspiegel im Winkel von 45° im Strahlengang steht. Jetzt
wird die Power dadurch sichtbar, weil über die Sphäre mit mehreren Kilometern Durchmessern, Astigmatismus als Fehler eingeführt wird.
http://www.reinervogel.net/index_e.html?/lowrider/plan_e.html, dieser Link wäre u.a. ein Beweis dafür. Die Power wird
also erst sichtbar, wenn man in einem flachen Winkel über die Planfläche "schaut", wie in dem Link beschrieben. Diese Technik ist
nicht neu, auch Vasco Ronchi kannte das schon.
Wer also Planflächen herstellt, tut gut daran, die Planfläche auch auf diese Weise zu prüfen. Auf der Basis eines IGrammes bei 532 nm wave
hätte ich einen Radius von 29.7 km auf der fraglichen Planfläche ermittelt, jedenfalls groß genug, um die Abbildung zu stören, wie die Fotos
beweisen.
Nun nützt es allderdings gar nichts, wenn man senkrecht auf den ellipt. Planspiegel prüft: Dann verschwindet nämlich die
Power. Man muß entweder den Strahlengang so legen, wie er im Newton-System vorliegt, oder aber man hat eine
absolute Referenzfläche, deren Restfehler man möglichst noch kennt, und dann kann man berührungslos den ellipt.
Planspiegel prüfen, der vorher natürlich mindestens 2 Stunden temperiert sein sollte.
Auffällig ist im übrigen, daß der Hersteller nicht seine Test-Ergebnissen vorlegt, damit man dessen Messungen nachvollziehen könnte.
##########################################################################################
Testaufbau mit 120 mm Parallel-Bündel-Durchmesser
Ob sich der bisher noch ungenannt bleibende Hersteller erweichen läßt, seine Test-Methoden offen-zu-legen, ist noch nicht erwiesen.
Vorgestellt werden soll eine weitere Möglichkeit, den ellipt. Flat mit 170 mm Durchmesser auf realistische 120 mm Durchmesser zu
prüfen. Die Prüfung gegen eine Sphäre, wie im obersten Bericht vorgestellt, prüft die gesamte Fläche des Fangspiegels, die aber in
einem Newton-System nur mit Durchmesser 120 mm beansprucht wird. Nur diese Fläche, die ca. 50% der Gesamtfläche darstellt,
muß die jeweilige Genauigkeit haben, also ohne signifikanten Astigmatismus abbilden.
Im ersten Schritt stellt man den TSA mit 120 mm Durchmesser gegen einen Planspiegel in Autokollimation. Damit wird ermittelt, mit welcher Genauigkeit
der TSA 120 den Artificial Sky Test abbildet.

Die Abbildung entspricht in jedem Fall der Formel und das Foto beweist, daß die Abbildung sogar unter 1" arcsec liegt, ohne irgendein Anzeichen von Astigmatismus,
was man zunächst dem TSA selbst zuordnen müßte, der zweimal im Strahlengang steht. Der TSA eignet sich daher als Referenz-Optik.
.

.
Im zweiten Schritt fügt man einen weiteren Planspiegel ein mit dem Ziel, nunmehr den Zeiss-Werkstatt-Spiegel im 45° Winkel aufzustellen, also in gleicher
Position, wie auch der ellipt. Fangspiegel in einem Newton-System positioniert wird. Wäre nun auf dem Zeiss Werkstatt-Spiegel ein signifikanter Radius,
auch Power genannt, dann sollten astigmatische Figuren beim Artificial Sky Test zu beobachten sein.

.
Stattdessen beweist aber das Testbild, daß beide Planspiegel keine nennenswerte Power aufweisen, also eine hohe Planität haben. Und genau das wird auch
vom ellipt. Flat erwartet, der später gegen den Zeiss Werkstatt-Spiegel getauscht wird.
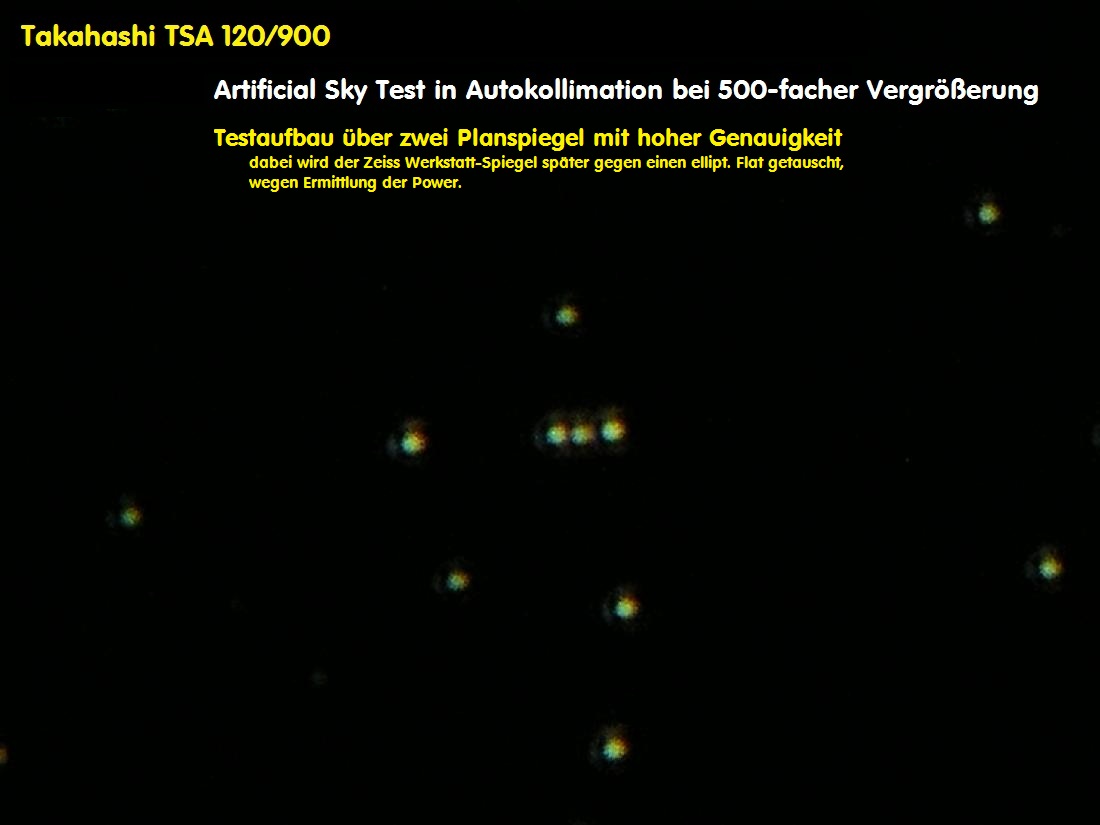
Auf dieses Ergebnis warten wir morgen mit Spannung . . .
Dann kann über ein Interferogramm der Astigmatismus der Grundordnung ermittelt werden, und darüber dann die Power, bzw. der Krümmungs-Radius
der Fläche selbst, der im Kilometer-Bereich liegen muß.
##########################################################################################
Ob nun der Hersteller die von ihm selbst proklamierten Genauigkeits-Angaben - bezogen auf die gesamte Planspiegelfläche - erfüllt hat, ist von eher
untergeordneter Bedeutung, die sich höchstens im Preis-Leistungs-Verhältnis ausdrückt. Für einen LOMO-Spiegel müßte man den 4-fachen Preis
bezahlen, hätte aber dann eine größere Sicherheit und auch noch ein Zertifikat. In unserem Fall rückt dieser Hersteller keine nachvollziehbaren
Beweise heraus und gibt stattdessen die "beleidigte Leberwurst".
Die entscheidende Frage ist vielmehr, ob dieser Planspiegel, wenn er im Newton-System jeweils nur eine Fläche mit Durchmesser 120 mm kleine
Achse beansprucht, ob er wenigsten für diesen Fall tauglich ist. So wurde also nicht mehr die gesamte Fläche auf Genauigkeit geprüft, sondern
die tatsächliche benutzte Fläche auf Tauglichkeit. In diesem Zusammenhang wurde das TSA 120/900 von Takahashi verwendet, das exakt
diese 120 mm Durchmesser darstellt, indem ein Parallel-Bündel von 120 mm den Flat zweimal unter 45° trifft.
Übrigens hat dieser relativ "dicke" Planspiegel eine längere Auskühlzeit.

Auch bei eingeschränkten, aber realistischem Durchmesser von 120 mm sollte eigentlich kein Astigmatismus mehr zu sehen sein, der TSA selbst führt keinen ein.
Am oberen Ende schlägt der Astigmatismus mit PV L/3.6 zu Buche, man sieht es dem Interferogramm deutlich an. Die Frage lautet deshalb, ab welcher Vergrößerung
würde man diesen Sachverhalt erkennen?
Auf der "gegenüberliegenden" Seite, also rechts bzw. vorne oder unten, ist die Situation umgekehrt: Hier taucht nun ein Koma-Effekt auf, der den PV-Wert für
Astigmatismus noch übertrifft. Die Figuren, die der Artificial Sky Test abliefert, zeigt die Situation.
Weil es aber ein Newton mit einem 600 mm Spiegel ist, mit großem Öffnungsverhältnis und Gitterrohr-Tubus, stellt sich auch die Frage, welche Höchstvergrößerung damit
realisierbar ist, und ab welcher Vergrößerung man diese Situation merken würde. Die Wahrnehmung für derartige Restfehler wird unterschiedlich angegeben. Ein versierter
Beobachter würde noch PV L/6 sehen, nach meiner Auffassung ist die Wahrnehmungsschwelle eher bei PV L/3 - L/4.
Die Sternfreunde müssen sich also entscheiden, wobei mich selbst am meisten interessiert, wieviel von den im Labor gemessenen Restfehlern in der Praxis zu sehen sind.
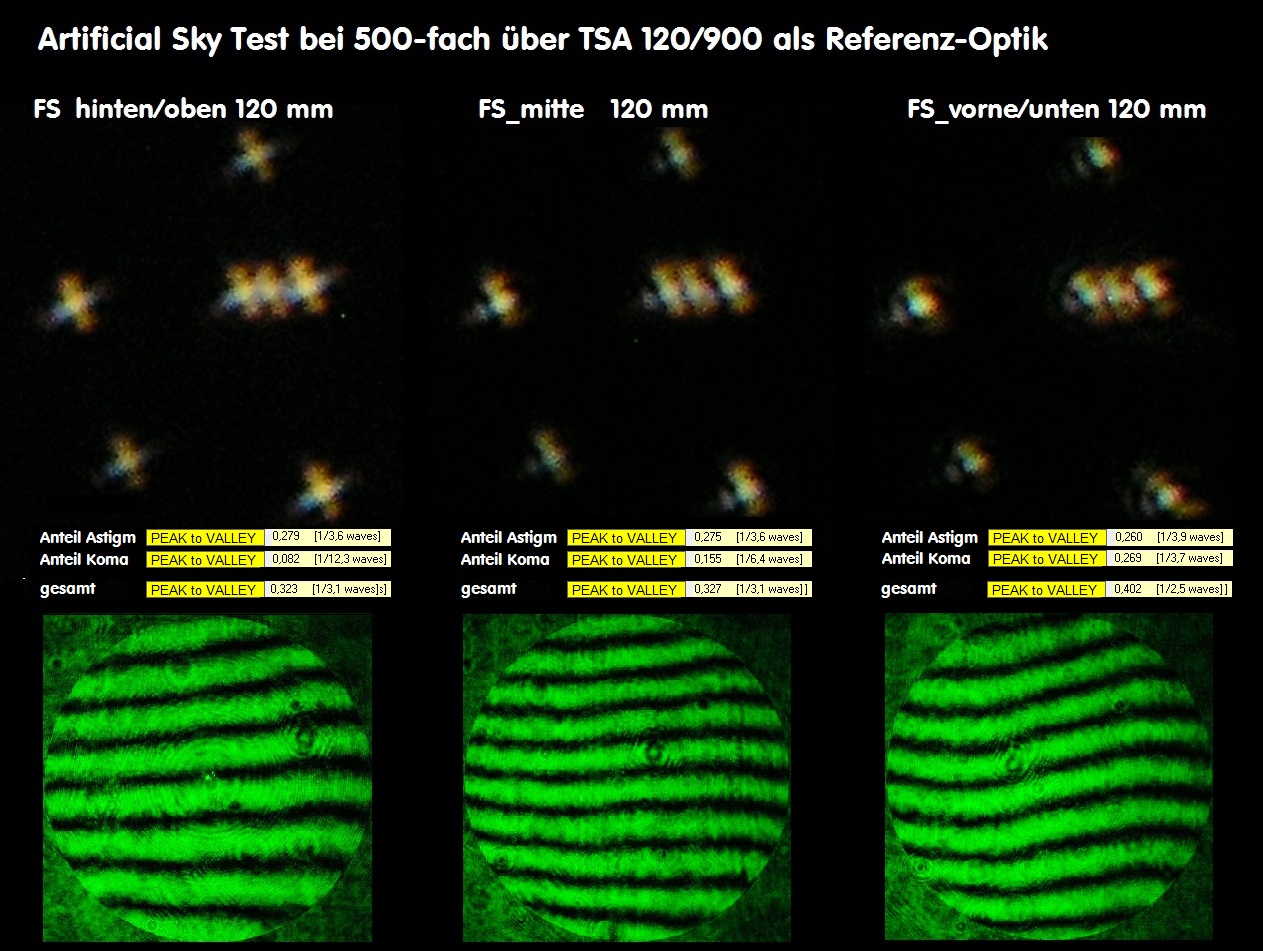
E045A Fangspiegel testen verschiedene Setups
Bei einem Newton-System wird dem elliptischen Fangspiegel (Flat) in der Regel zu wenig Aufmerksamkeit geschenkt. Selbst der allerbeste
Newton Hauptspiegel kann von einem unbrauchbaren Fangspiegel regelrecht ruiniert werden. Deshalb könnte man diesen Sachverhalt auf
mehrere einfach Weise selbst prüfen:
Im Fall a) einfacher Durchgang braucht man als Hilfmittel ein perfektes kleines Teleskop (ED-APO oder APO). Mit diesem Teleskop schaut man sich einen
10 - 20 m entfernten künstlichen Stern unter hoher Vergrößerung an. In beiden Fällen sollte die Abbildung gleich gut sein.
Im Fall b) doppelter Durchgang ist die Lichtquelle im Fokus des Teleskopes. Nach dem Objektiv geht das Parallel-Lichtbündel über den Flat zu einem weiteren
Flat wieder zurück bis zum Fokus des Teleskopes. Auch hier sollte die Abbildung der punktförmigen Lichtquelle gleich aussehen.
Für den Fall c) doppelter Durchgang ist eine Sphäre im Bereich R/4 nötig. In meinem Fall u.a. 150 R 600. Auch hier verläuft der Lichtkegel von der Quelle
über den Flat zum Kugelspiegel und wieder zurück. Die Abbildung sollte sich in dieser Testanordnung ebenfalls nicht verändern.

E007 Fraunhofersche Spektral-Linien im sichtbaren Teil des Spektrums
Der Unfug mit dem Polychromatischen Strehl
24. November 2009
Der Stein der Weisen ist es nicht, auch wenn zwei User vehement den Versuch starteten, mich hier zu
"bekehren". Wer viel mit der Vermessung von Optiken zu tun hat, wünscht sich zumindestest eine
entspannte und unaufgeregte Diskussion, die die Sache selbst im Blick hat, statt ein friedliches Forum
aufmischen zu wollen. Aus diesem Grund bleibt dieser Beitrag geschlossen !
Lesenswert auch diese Beiträge dazu: http://www.groupsrv.com/science/about408319.html
Vorbemerkung:
Den auf Astrotreff und A.de unter großem zeitlichen Druck veröffentlichten Messungen zum oberen
Begriff fehlt die logische Systematik und vermittelt lediglich den Eindruck von Aktionismus. Der Takahashi-
Link funktioniert nicht mehr(siehe deshalb unten), lediglich die zwei TMB-Tabellen sind verfügbar als
einizge Legitimation, die Szene mit "neuen Erkenntnissen" zu beglücken. Dort findet man nur Einzelstrehls,
nicht jedoch einen PolyStrehl als Zahl oder Diagramm. Der Ursprung solcher Diagramme stammt somit ein-
deutig aus optical Design Programmen. Ein seriöser Vergleich scheitert also bereits an der geringen Zahl
der Veröffentlichungen selbst und deren Vergleichbarkeit.
Vor einer ernstzunehmenden Diskussion müßten daher u.a. folgende Fragen einvernehmlich geklärt werden:
Quote:
- welcher Informations-Gewinn entsteht durch einen selekt.PolyStrehl im Vergleich zur umfassenderen RC_Indexzahl
- für welches astronomische Fernrohr ist ein selektiver Polychromatischer Strehl sinnvoll = klare Eingrenzung des Bereiches
- gibt es klar festgelegte Spektren, in denen gemessen werden soll, wie z.B. die Fraunhofer'schen Linien und
- gibt es klare Regeln für deren Gewichtung im Rahmen einer Polychromatischen Vergleichszahl, ist das TAk-Beispiel richtig und bindend?
- gibt es eine klare Beschreibung bzw. Begrenzung, wo eine PolyStrehl-Zahl sinnvoll/sinnlos wird.
- gibt es ernstzunehmende Quellen als Beleg, daß dieser Begriff Eingang gefunden hätte in die Meßtechnik !
- müssen Fertigungsfehler um der Vergleichbarkeit willen zu anderen Systemen herausgerechnet werden oder nicht, analog der Situation beim Design.
An der Frage, ob Fertigungsfehler der Vergleichbarkeit dienen oder sie verhindern, scheiden sich bereits die Geister.
Chronologie der Thematik
Am 12. März 2009 taucht der Begriff Polychromatischer Strehl über den Beitrag eines befreundeten
Designers erstmalig hier auf. Über folgende ZEMAX-Diagramme wurden über diesen Begriff die Unter-
schiede zwischen ED-APO's und Tripletts herausgearbeitet. http://rohr.aiax.de/@APOVergl01.jpg;
http://rohr.aiax.de/@APOVergl02.jpg; http://rohr.aiax.de/@APOVergl03.jpg
In der Folge wurde der gleiche Begriff von zwei bekannten Usern auf A.de und Astrotreff.de in einer
sehr verkürzten und unsystematischen Form regelrecht in Beschlag genommen. Ein Jahr früher, am
04. Juli 2008 veröffentlichte ich folgenden Bericht auf Astro-foren.de: Weißlicht-Bath-Interferometer für Massimo
In Beitrag #4 veröffentlichte ich mehrere Farb-Interferogramme in den Spektral-Farben, wie sie von
Optik-Designern beim Entwurf von Astro-Optik Verwendung findet.
Das fand frühestens am 01. Dez. 2009 seinen unsystematischen Niederschlag in einem Bericht hier:
http://www.astrotreff.de/topic.asp?TOPIC_ID=95328 Offenbar tut sich der dortige Beitrag schwer
mit den üblichen Spektral-Bereichen durch unübliche Wellenlängen. Die in diesem Zusammenhang
als "PolyStrehl-Diagramme" zu verkaufen beweist, daß das grundsätzliche Wissen fehlt. Auch eine
Quellenangabe fehlt, so daß man den Eindruck gewinnt, der dortige Verfasser holt sich regelmäßig seine
Anregungen auf unserem Forum und präsentiert dann dort das Ergebnis ungeniert als seine eigene
Entwicklung, auf die er im Bedarfsfalle noch geistiges Eigentum beansprucht. Noch nicht genug,
starteten zwei User aus diesem Dunstkreis auf unserem Forum den Versuch, uns mit wenig höflichen
Beiträgen ihre Sichtweise regelrecht aufzwingen zu wollen.
Ursprung aus Optical-Design-Programmen
Der Begriff polychromatischer Strehl, wie er als Tabelle(*) im Zusammenhang mit TMB und Takahashi-
Objektiven(**) veröffentlich worden war, ist das Ergebnis eines Optical Design Programmes, n i c h t
das Ergebnis einer realen Messung. Damit bleibt dieser Begriff im Bereich des Designs und ist nur
dort auf gleicher Ebene mit einem anderen Design vergleichbar und sinnvoll. Außerhalb dieses klar um-
rissenen Bereiches wird dieser Begriff mißbraucht, um verbissene, abgehobene Diskussionen zu führen
über den untauglichen Versuch, Farblängsfehler gemeinsam mit dem Gaußfehler in einer Indexzahl für
alle Refraktoren zu verknüpfen. Dabei ist man sich nicht der Schwächen bewußt, die dieser Begriff in
der Meßpraxis zeigt. Ein Optical Design Programm stellt also nur die theoretisch optimale Situ-
ation dar, aber keinesfalls Fertigungs-Fehler, wie systemübergreifende Überkorrektur, Flächenfehler,
Zentrier- Fehler, Astigmatismus etc. Diese Fertigungs-Fehler tauchen in diesem von Mathematik und
Design dominierten Bereich zumindest auf der Achse zunächst noch gar nicht auf.
Mir ist also kein allgemeiner Konsens bekannt, wie mit diesem Begriff exakt umzugehen sei.
Unvollständige Systematik:
Die auf den anderen Foren veröffentlichten Farb-IGrammen beweisen nur, daß Kurt nach drei Jahren
Anlaufzeit sein Equippement soweit vervollständigt hat und ein User Gerd das Zeichnen von Diagrammen
für informativ hält. Die Systematik des polychromatischen Strehls ist insofern unvollständig, als die
Betrachtung nicht nur auf die opt. Achse beschränkt bleiben dürfte, sondern auch auf die Situation im
Feld bezogen werden könnte, wie es Spotdiagramme ja tun. Im Bereich des Polychromatischen Strehls
käme man aber zu unsinnigen Ergebnissen, weil der Strehlwert über den Astigmatismus und/oder Coma
im Feld rapide sinkt und damit seine Aussagekraft verliert. Ähnlich verhält es sich bei Achromaten
auf der opt. Achse, wo der Farblängsfehler den Strehl über die Power gegen Null drückt, was einige der
Diagramme bereits sehr anschaulich beweisen. Ebenso fachfremd ist die Forderung, aus dem bisher üblichen
Strehl einer Meßwellenlänge, über alle Wellenlängen des sichtbaren Spektrums einen gewichteten Polychro-
matischen Strehl zu ermitteln, was bereits in der praktischen Durchführung mit vielen Hypothesen und Ein-
schränkungen versehen ist, und damit ohne jeden Nutzen für eine bessere Vergleichbarkeit von Refraktoren
untereinander. Die jahrzehntelangen bewährten Tests sind in jedem Fall viel effektiver und aussagekräftiger,
weil bereits ein ganz normales Zertifikat von den wenigsten verstanden wird. Siehe hier.
Dem entgegen steht auch die in der optischen Industrie gängige Interferometer- bzw. Phasen Shift
Interferometer-Meßtechnik, die in der Regel bei 632.8 nm Wellenlänge eines Helium Neon Lasers
arbeitet. Oder in Form eines Fizeau- oder Twyman-Green Interferometeres bei 532 nm wave, dann
im grünen Spektrum. Mit einer solchen Ausrüstung ist ein polychromatischer Strehl eine Utopie,
weil interferometrisch überhaupt nicht darstellbar. Es fehlen nämlich die Interferogramme im
kurzen Spektrum, also z.B. bei 486.1 nm wave, was der F-Linie bei Fraunhofer entsprechen würde.
Daran ändert auch die Fleißarbeit eines Kurt nichts: Dieses Bild notfalls über die CopyFunktion
eingeben: <<|http://www.astrotreff.de/upload/Kurt/20091201/Bi14.jpg|>> hier. Seite 4
Die Anregung holte er sich hier: http://rohr.aiax.de/@Sepktral-Farben.jpg
http://www.astro-foren.de/showpost.php?p=37052&postcount=4 Wobei auffällt, daß er sich an
keinerlei Konvention hält.
Damit sollte man sich erst einmal begnügen, bevor man den Versuch startet, innerhalb der Meß-
technik selbst den Polychromatischen Strehl lauthals zu fordern. Selbst wenn er in irgendeiner
Weise zu realisieren wäre, ist die Vergleichbarkeit mit anderen Systemen das oberste Ziel,
und dann müssen, wie im Bereich des Designs, zu aller erst die Fertigungs-Fehler herausgerechnet
werden - sonst vermischt man nämlich Fertigung mit Design. Man würde einen TMB nur deswegen
schlechter darstellen, weil er wegen der Fassung astigmatisch reagiert. Ein Zeiss APQ, der zufällig
diesen Fehler nicht hat, würde dann besser abschneiden, eine Info zum Gaußfehler hätte man dann
aber nicht. Bei dem folgenden Zeiss APQ Nr. 011 hätte man z.B. zwei unterschiedliche PolyStrehl-
Werte, abhängig davon, ob mit oder ohne Astigmatismus, oder abhängig ob mit oder ohne Glasweg.
Der Astigmatismus war nämlich über einen Fehler mit dem Immersions-Gel entstanden, und wurde
deshalb behoben. Deshalb steht die Forderung, alle tatsächlichen Fehlerquellen in den Polychromatischen
Strehl aufzunehmen, der eigentlichen Absicht entgegen, Aussagen über den Gaußfehler zu machen.
APQ 105/800 Spannend wie ein Krimi - extrem farbrein
APQ 105/800 zweite Untersuchung nach Überarbeitung
Farblängsfehler-Vermessung
Nun war es wiederum meine Anregung vor ca. 3 Jahren, in definierten Spektren, also von der
h-Linie, g- und F-Linie, über e-Linie, d-Linie und C-Linie mit Hilfe von engen Interferenzfiltern mit einer
Bandbreite von ca.10 nm üblicherweise, Interferogramme fotografisch zu erstellen. Das aber nicht,
um der polychromatischen Strehl-Diskussion Vorschub zu leisten, sondern um die vermutlich
genaueste Möglichkeit darzustellen, wie man den Farblängsfehler auf der opt. Achse vermessen kann.
Das geschieht über die Streifen-Verkippung in den jeweiligen Spektren, wenn man die Streifen bei der
Hauptfarbe Grün auf Null stellt und die Abweichung bei Blau und Rot ausmißt, eventuell über den Power-
Betrag umrechnet, was aber ebenfalls mit Einschränkungen verbunden ist.
Ziel dieses Verfahren ist und bleibt die interferometrische Vermessung des Farblängsfehlers
eines Objektivs auf der opt. Achse, der eine RC_Indexzahl abliefert, über die alle Refraktor-Objektive in
ein überschaubares System einsortiert werden können. So machte es bereits Lichtenknecker vor
30 Jahren in seinen Tabellen, so machte es Zeiss ebenfalls, deren Optikrechner allerdings den Weg
über das optische Desing gingen, das mir bei einem Objektiv in der Regel unbekannt ist, weswegen
nur die Möglichkeit bleibt, den Farblängsfehler einer Optik real mit einer tausendstel Meßuhr in Form
von Reihenmessungen zu vermessen und diese dann zu mitteln. Über dieses Verfahren kommen bei
Refraktor-Optiken selbst aus der gleichen Serie oft differierende RC-Werte heraus, was mit dem
nicht immer gleichen Linsenabstand der Objektive zu tun hat. Die Anordnung der Farben bleibt aber
in er Regel erhalten, die ändert sich z.B. nur bei Verwendung eines Glasweges. Wenn, wie beim
Equinox passiert, der angegebene Objektiv-Durchmesser heimlich über okularseitige Blenden verkleinert
wird, dann nimmt ebenfalls die "Farbreinheit" zu, in der Hauptsache durch eben dieses Abblenden,
was zu einem sehr guten RC_Wert führte. Hier wurde ein deutlich überkorrigiertes 4.000.- Euro
teures FLT mit einem farbreinen Equinox verglichen, für den man ca. 1.500.- Euro zu bezahlen hatte.
In einem engeren Bereich zwischen manchen ED-APO's oder Triplets gewinnt der Gaußfehler
stärker an Bedeutung und es geht um die Frage, wie man im Vergleich zu einem anderen Objektiv
diesen Gaußfehler-Unterschied gewichten kann. Es geht also erneut nur um den Gaußfehler-Anteil
einer Optik in PV- oder Strehlwert, und nicht um weitere Fehler, die diese Optik vielleicht hat oder
auch nicht. Vergleichbar sind hinsichtlich des Gaußfehlers Optiken nur, wenn man - wie beim
Farblängsfehler auch - dieser Gaußfehler isoliert betrachtet wird, wobei der Gaußfehler durchaus
über einen Strehlwert oder PV-Wert dargestellt werden könnte, wenn man die Größe mit anderen
Systemen vergleicht. Und nur um der Vergleichbarkeit willen, muß man den Gaußfehler isoliert
betrachten, wie das auch bereits im Bereich des Desings so gehandhabt wird. Dort wird nämlich
nicht ein Polychromatischer Strehl angegeben, sondern lediglich in Tabellenform die spektralen
Einzelstrehls genannt, die man unter ZEMAX noch nicht einmal in einer Tabelle aufgelistet bekommt,
sondern einzeln ermitteln muß. Bereits die wenigen Veröffentlichungen legen nahe, daß über die
Einzelstrehls im Bereich Design hinaus aus gutem Grund kein Polystrehlwert in den Veröffentlichungen
selbst angegeben wird.
Wer im Jahre 2009 z.B. von LZOS ein hochwertiges Triplet kauft, bekommt üblicherweise ein
Zertifikat innerhalb der Hauptwellenlänge, in diesem Fall bei 532 nm wave. Also nicht etwa bei
Blau, Grün, Gelb und Rot und nicht etwa als Polystrehl über diese vier Farben dargestellt. Und
jeder halbwegs aufgeklärte Kunde weiß, daß Gaußfehler-bedingt im blauen Spektrum der Strehl
etwas niedriger ist, ebenso im roten Spektrum. Das über blaue oder rote Farbinterferogramme
nachzuweisen, würde allenfalls ein Kopfschütteln bei den Feinoptikern hervorrufen. Mit einer Meß-
wellenlänge von 532 nm ist dem gesamten Sachverhalt bereits ausreichend geschuldet, schon weil
der Strehlwert nur ein Kriterium in der Beurteilung von Refraktor-Optiken darstellt.
Und selbst wenn nun das Bath-Interferometer stärker zum Zug kommt mit seiner Fähigkeit, im
gesamten Spektrum Interferogramme zu erzeugen, dann käme erst einmal wieder die Forderung
der gemittelten Vielfachmessung im Einzelspektrum mit der ebenfalls nicht geklärten Gewichtung
der Teil-Ergebnisse zur Hauptfarbe Grün. Es entsteht also ein kompliziertes Gespinnst, das Zug
um Zug an Informations-Wert verliert, gefolgt von einer aggressiven Foren-Diskussion über
vernachlässigbare Größen und Details.
Im weiteren Verlauf entstehen dann mindestens zwei Strehl-Werte: Erstens der bisherige Strehl-
Wert, der innerhalb der Hauptfarbe oder dem tatsächlichen Optimum Aufkunft gibt über die
quantitative Qualität eines Objektivs und ein weiterer komplizierter PolyStrehl-Wert, der hauptsächlich den
Gaußfehler darstellen soll bei hochwertigen APO's. Bei einem Achromaten würde dieses Verfahren
den Strehl endgültig ins Bodenlose ziehen ohne jede Aussagekraft. Man hätte eine abgehobene
"Experten-Diskussion", die erfahrungsgemäß ganz andere Ziele verfolgt, als sachliche Information.
Ein Hersteller, Händler oder auch Kunde würde vollends den Überblick verlieren, bis auf diejenigen,
die glauben, mit dieser herstellungs- und praxis-fernen Idee zur "Aufklärung" beizutragen.
Vielleicht denken diejenigen den Sachverhalt in aller Gründlichkeit erst selbst einmal durch, bevor
sie mit unausgegorenen Forderungen die Szene überziehen.
Dabei geht es n u r um eine schlüssige Unterscheidung, was ist ein APO und was nicht.
Bereits die Vergleichbarkeit zwischen TMB und Takahashi ist nur eingeschränkt möglich!
Bei TMB fehlt die Gewichtung, Takahashi verwendet anderen Spektren.
Ungewichtete Tabelle spektraler Einzelstrehls: Quelle (*)
Der Orginal-Link funktioniert nicht mehr:
Quote:
Darstellung des Farblängsfehlers: Quelle (**)
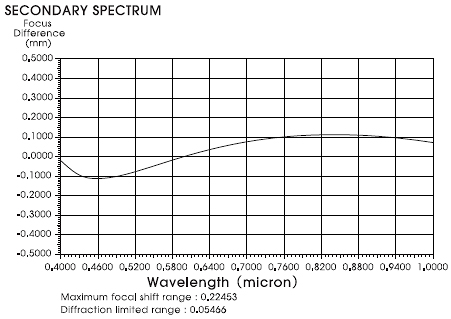
Zur gleichen Thematik:
farbige Weißlicht-Interferogramme Zusammenfassende Übersicht
#####################################################################################################
Stichwort: Frequenzkamm
http://de.wikipedia.org/wiki/Frequenzkamm
http://www.kosmologs.de/kosmo/blog/galaxienentwicklung/entdeckungen-und-methoden/2008 -09-07/frequenzkamm-einsatzbereit-f-r-astronomische-beobachtungen
http://www.quantum.physik.uni-mainz.de/lectures/2007/ws0708_laserphysik/Kapitel7.pdf
Erzeugung von monochromatischem Licht
Monochromatisches Licht bekommt man immer, wenn Licht durch ein lichtbrechendes Medium fällt, im einfachsten Fall ein Prisma. Im Spektroskop
findet dieser Sachverhalt ebenso seine Anwendung, wie im Spektrometer, mit dem man das jeweilige Spektrum ausmißt. Dafür bekam u.a. Prof. Theodor Hänsch 2005 den Nobelpreis für Physik: Quote:
„für Beiträge zur Entwicklung der laserbasierten Präzisionsspektrographie, einschließlich der Technik des optischen Frequenzkamms“
Das untere Beispiel wurde mit einem 600 lp/mm LinienGitter erzeugt, ebenso die Farbauszüge.
Dabei müssen für einen regelbaren Interferenz-Filter zwei Bedingungen erfüllt sein:
- Über eine Regeleinheit muß man sich nachweisbar exakt in der gewünschten Wellenlänges befinden, also genauer als die üblichen engen Interferenzfilter
- die Lichtintensität muß über ein System soweit verstärkt werden, daß damit im weiteren Verlauf stufenlose Farb-Interferogramme möglich sind. Die Details kann sich der interessierte Leser per Email bei mir abholen.

#####################################################################################################
Uwe Süßenberger schickte mir folgenden Link: http://www.telescope-optics.net/polychromatic_psf.htm
Unter dem Titel: "Measuring chromatic error in an achromat: polychromatic PSF" werden genauge-
nommen Ergebnisse veröffentlicht, wie man sie mit Optical Design Programmen wie Oslo generieren kann und
als generelle theoretische Vergleiche für einen Optik-Designer durchaus interessant sein können. Nur bedeutet
das nicht, daß die dort gezeigten Diagramme das Ergebnis von konkreten Messungen an einem Einzel-Teleskop
wäre. Derartige Beiträge zeigen erneut, daß ein großer Unterschied besteht zwischen der im Bereich Design
anzusiedelnden Theorie-Diskussion, die es mit ideal-typischen Systemen zu tun hat, und den praktischen Niederungen
bei der Vermessung konkreter Optiken, bei der es immer auch um Fertigungsfehler geht. Solange man also die beiden
Bereiche sorgfältig trennt und für sich betrachtet, gibt es keinen Anlaß für irgendeine Diskussion. Nur mischen kann
man es aus vielen prinzipiellen Gründen nicht, solange über die Kriterien keine Einigung erzielt wurde. (1. Beitrag oben)
Quote:
◄ 4.8.1. Secondary spectrum and spherochromatism ▐ 5. INDUCED ABERRATIONS ►
4.8.2. Measuring chromatic error in an achromat: polychromatic PSF
Summing it up, an achromat optimized for a particular wavelength, will have spherical aberration canceled for that wavelength, and chromatic aberration nearly cancelled laterally, while reduced to nearly ƒ/2000 of the F/C secondary spectrum. The error at the optimum focus results from other wavelengths being: (1) defocused, and (2) affected by spherical aberration, with the latter being comparatively low or negligible. The main error component, that of chromatic defocus, can be expressed as a P-V wavefront error:
W= Pr2(51)
with P=-Dƒ/8F2 being the peak aberration coefficient, equal to the P-V wavefront error, and r the pupil ray height in units of the pupil radius. This error combines with the error of spherochromatism for that particular wavelength, and the combined error is finally "measured up" by the sensitivity factor of the eye.
With Dƒ being, for typical achromats, ~ƒ/2000 at best, the P-V wavefront error of chromatic defocus for an achromat can be written as W~D/16,000F at its red and blue foci. For D=100mm and F=10, this gives 0.000625mm, or 1.29 wave P-V of defocus for the blue F-line (λ=0.000486mm), and 0.95 wave P-V of defocus for the red C-line (λ=0.000656mm).
For film/CCD applications, defocused wavelengths are more to much more detrimental, depending on both, characteristics of the chromatic defocus and spectral sensitivity of the detector. For instance, most achromats have defocus error significantly greater toward the blue/violet end, which would seriously impair performance with a detector with high sensitivity for that range. However, if the detector is relatively insensitive in the blue/violet, a decent to good results can be achieved even with relatively fast achromats, with significant gross chromatic errors.
Contrary to the common misconception, nominal chromatic defocus is not an accurate indicator of the level of chromatism, in the sense that the two change at a different rate with the change in either aperture D or focal ratio F. For instance, while the defocus error at any wavelength other than the optimized doubles with either doubling D or halving F, resulting chromatism - measured by the drop in polychromatic peak diffraction intensity (PPDI) - will increase at a significantly slower rate. This is what advanced optical design software programs, using diffraction calculation, imply.
Note that PPDI ratio number normalized to 1 for zero chromatism is sometimes called "polychromatic Strehl"; while the rationale for such term is that it does indicate relative central intensity of diffraction pattern, with secondary spectrum it results not from wavefront deformation, but from defocus error of many separated wavelength-determined wavefronts. In order to make distinction with respect to a common use of the Strehl indicator as an indicator of wavefront quality, the relative central intensity resulting from chromatic errors will be termed directly as PPDI.
The reason for this "strange" behavior is that much of defocused light of the farther-off-optimal wavelengths is already out of the Airy disc, and merely gets spread out wider (for instance, F and C line in the 4" ƒ/10 above have only a few percent of the energy left within the Airy disc). The spectral range relatively close to the optimized wavelength also doesn't contribute "new" lost energy, since it is not affected. It is only a relatively narrow spectral segment on either side of the optimized wavelength, which previously had relatively small amount of energy outside the Airy disc, that adds significant new energy to that already transferred outside of the Airy disc. A parallel can be drawn between any far-from-focus wavelength, or a narrow spectral range, and a surface error limited to a relatively small area. Such a surface error keeps draining more energy from the Airy disc with the increase in the nominal error only up to the point when practically all the energy available from that area is lost. After that, there is no appreciable effect from the further error increase. This is why turned edge behaves as it does, or any wavefront error limited to a relatively small area. For instance, a zone 1/10 of pupil radius wide, at half the radius, going from 1 to 2 waves P-V, won't change neither peak intensity value (0.96) nor encircled energy (0.95), despite the consequent doubling of the nominal and - at 0.22 and 0.44, respectively - rather substantial RMS error. Heavily defocused far wavelengths in an achromat are pretty much like an aerially small, nominally large, and effect-wise mainly drained out wavefront error.
This explains surprisingly good performance of fast achromats in general - and particularly large fast achromats - which, according to their nominal secondary spectrum, should be hardly useable at all.
As it often goes in life, there is the bad side to it as well: it is that the PPDI also improves at a slower rate with the decrease in nominal chromatic defocus; in other word, halving the focal ratio doesn't halve the chromatism. The good news is that the discrepancy between decrease in nominal defocus error and the actual chromatic error is significantly smaller here.
While the PPDI is a reliable general indicator of the effect of aberration over the range of resolvable frequencies, it gives no information about more specific effects on contrast transfer at within sub-ranges of frequencies that could be of interest. In particular, how the effect of chromatism compares to spherical aberration effect at mid-to-low MTF frequencies (details approaching Airy disc diameter, and larger; the range of planetary and deep-sky observing) and near the stellar resolution threshold. Differences in this respect can be suspected based on distinctly different form of energy distribution caused by chromatic error. Due to increasing defocus error for non-optimized wavelengths, diffraction pattern has a form similar to one caused by monochromatic defocus: the first dark ring is filled with energy, with its contrast deep significantly reduced.
As a result, at any given nominal peak intensity (within the range commonly encountered with amateur telescopes), diffraction pattern affected with chromatism has higher encircled energy fraction within the Airy disc than what is indicated by the peak value. For instance, while the PPDI of a 100mm f/12 doublet achromat is 0.77, the encircled energy within the Airy disc is 0.83. It is generally higher than the encircled energy fraction with spherical aberration at the same nominal peak intensity (which is nearly identical to the encircled energy fraction). On the flip side, brightening of the first dark ring caused by chromatic defocus does have negative effect on the efficiency of contrast transfer. The combined effect of these two opposing factors, as the MTF plots bellow illustrate, is better contrast transfer at mid-to-low frequencies, and lower in the 0.5-0.8 frequency range (approximately).
The graphs bellow (FIG. 48) illustrate:
(1) how the peak of polychromatic PSF of a standard doublet achromat - and with it the effect of secondary spectrum on image quality - changes with the change in F and D,
(2) the effect of the form of intensity distribution caused by secondary spectrum on contrast transfer, with comparison to the effect of spherical aberration, and
(3) PPDI and contrast transfer in an achromat compared to an apochromatic refractor.
Both, PPDI and MTF are calculated by OSLO, based on 25 wavelengths from 440nm to 680nm (10nm increment), weighted for the photopic eye sensitivity, for the standard (Dƒ~ƒ/1920) C-e-F Fraunhofer doublet achromat (the same polychromatic input is used for calculating comparative effects of spherical aberration).
FIGURE 48: Effect of chromatism on image quality in terms of standard indicators of optical quality - central diffraction intensity and contrast transfer efficacy - allows for its direct comparison with other forms of aberrations.
(1): Polychromatic peak diffraction intensity (PPDI) in a standard Fraunhofer-type doublet achromat as a function of aperture size and relative aperture has significantly different rate than change in the nominal chromatic defocus (secondary spectrum). While there is no simple accurate expression for it, the change in PPSF can be fairly well approximated with simple relations fitting into actual values. In any instance, the detriment of chromatism with the increase in aperture size - or reduction in relative aperture - is much smaller than corresponding nominal increase in the defocus error (secondary spectrum) caused by either of the two. Note that PPDI doesn't change with scaling doublet achromat while keeping the aperture to focal length ratio constant; a 100mm ƒ/12 has identical PPDI as 200mm ƒ/24. For a given aperture D in mm,the peak diffraction intensity (PPDI, or polychromatic Strehl) in function of the focal ratio F of the achromatis approximated by:
PPDI ~ 1.3(F/D)1/4
It stays close to the actual value for F/D smaller than ~0.25, which covers most practical instruments. For larger values of F/D it becomes too optimistic (it gives PPDI=1 for F/D=0.35, which corresponds to 100mm ƒ/35, or 200mm ƒ/70). For 0.25<(F/D)<1, better empirical approximation is PPDI~(F/D)0.07.

Expectedly, the contrast transfer efficiency of an achromat in this frequency range is somewhat higher than what its diffraction peak figure indicates, approximately at the mid level between the PPDI and the encircled energy (within the Airy disc) figure. The difference between the PSF indicated comparable level of spherical aberration, and that indicated by contrast transfer within mid-to-low MTF frequencies is roughly constant nominally - about 0.03 on the in the f/6 to f/24 relative aperture range. This implies that it is greater relatively in faster achromats.
On the other hand, there is no indications that brightening of the first dark ring caused by secondary spectrum, even in an achromat as fast as 100mm f/6, lowers limiting stellar resolution - inasmuch as the MTF graph can show this resolution aspect. In all, the particular form of intensity distribution within diffraction pattern in achromats results in more efficient contrast transfer within the range of resolvable extended details than with spherical aberration causing nominally identical drop in peak diffraction intensity (or central diffraction obstruction, considering its close similarity with spherical aberration in regard to intensity distribution for given relative peak intensity).
The overall perception is probably that long-focus refractors should have somewhat better optical rating. Most of this notion is the result of a general tendency of assigning to high-quality performers better optical quality than they really have. In other words, empirical criteria is based on the performance relative to other instruments; a telescope operating at a 0.9 Strehl overall optical quality, or even less, will be perceived as being close to perfection if other telescopes are operating at lower to significantly lower levels of optical quality - which is commonly the case.
A number of error sources that are invariably present are neglected or downplayed. For instance, a superb 6" Maksutov-Cassegrain telescope that goes with 0.96 Strehl optics will be operating far bellow that level in the field. In the average 2 arc seconds seeing, average seeing-induced error is around 0.1 wave RMS, enough to keep it bellow 0.7 Strehl level most of the time. It is not much better inside the tube: typical ~0.35D central obstruction alone lowers the 0.96 optics Strehl by 0.77 degradation factor, to 0.74. Thermally induced errors are all but likely to push it further down, bellow 0.7 Strehl level. Combine it with the seeing error, and you have an instrument performing merely above 0.5 Strehl - at best - mosYet it is regarded as a very good overall performer (misalignment error is not as much significant with Maksutov-type telescopes, as it can be with some others).
Compared to it, 0.74 peak diffraction intensity of a 6" f/15 achromat - or an effective ~0.77 for the range of resolvable extended details - doesn't look that much off. While it still suffers the same from seeing, it is significantly less affected by thermal errors. Since its chromatic error nearly offsets with the effect of Mak's central obstruction, it is likely to perform better in the field.
Following table shows nominal polychromatic PSF peak. It includes comparable amount of lower spherical aberration, and comparable central obstruction size (not adjusted for the effect of brighter central disk), with respect to relative intensity distribution within diffraction pattern and the resulting contrast level.
| Refractor |
[font='Tahoma'][size=10]TABLE 3: Approximate comparative effects of secondary spectrum (according to OSLO output) vs. spherical aberration and central obstruction. Encircled energy (EE) is within the Airy disc radius; mid-to-low frequency P-V error and C.O. size is based on the approximate empirical PSF peak equivalent to the actual contrast level, I~(PPDI+EE)/2 (note that larger APOs are upscaled 4" design; there is no technical obstacles for 6" or 8" ~f/10 APO to reach 0.95 PPDI level).[/align]
###############################################################################################################
Das neue Zauber-Wort: Monochromator
Das neue Spielzeug heißt Monochromator und kann hier bewundert werden. Bedauerlicherweise gibt es für die unterschiedlichen
Varianten bereits hoch-karätige Patent-Inhaber, sodaß man sich leider einer professionellen Konkurrenz stellen muß. Und damit
der Wissensdurst gestillt werden kann, hat eine Leihgabe das schmale Budget ein wenig unterstützt. Soweit der im Link erkennbare Vorgang.
Vom Gerät einmal ganz abgesehen, das bei Google/Bilder so aussieht wäre es eine Überlegung wert, was damit besser gemessen
werden kann, was eindeutig definierte Interferenzfilter von Edmund Scientific oder Melles Griot nicht zu leisten in der Lage wären.
Sind die bei Heinz Pforte "Der Optiker" Band 2 Theoretische Optik Seite 46 abgedruckten Fraunhoferschen Linien so überholt, daß
selbst bei TMB oder Takahashi-Diagrammen immer noch auf genau diese Spektral-Linien zurückgegriffen wird? TMB-SpotDiagramme
Während Interferenz-Filter exakt definiert sind hinsichtlich Spektralbereich und Bandbreite und Transparenz, baut die dortige Crew
über den ausgeliehenen Monochromator eine wunderbare Fehlerquelle ein über die Frage, bin ich exakt im vorgegebenen Spektrum
oder vielleicht doch nicht, stimmt meine Kalibrierung, stimmt meine Interpolation?
Der kurze Satz von Gerhard Polt trifft auch für diesen Sachverhalt zu: "Braucht's dös?"
Weltfirmen wie Zeiss und LZOS offenbar nicht, deren Zertifikate sind bei 632.8 nm wave erstellt, die älteren, bei LZOS wird schon
sehr lange bei 532 nm wave certifiziert, bei Zeiss vermutlich auch, wenn es sich um Refraktoren handelt. Und wenn man Refraktoren
vermessen will, beginnt das bei Achromaten mit großem Farblängsfehler/Gaußfehler-Verhältnis, über Halb-APO's, bei denen immer
noch der Farblängsfehler dominiert, bis hin zum Qualitäts-APO von Takahashi u.a. wo die Gaußfehler-Betrachtung endlich an
Bedeutung gewinnt, die eigentliche Ursache für diese imposante Anstrengung.
Statt Monochromator sind Interferenz-Filter einfacher, sicherer und überzeugender, weil sie Fehlerquellen ausschließen. Nicht
konsensfähig ist offenbar auch die Trennung von System-Fehler und Fertigungs-Fehler der Vergleichbarkeit zuliebe. Auch die Frage
der Gewichtung der Strehlergebnisse außerhalb der Hauptfarbe ebensowenig, wie die Hauptfarbe selbst: Soll es weiterhin
zwischen Grün und Gelb sein, oder vielleicht 510 nm wave, also der O_III Filter wegen der durchschnittlichen spektralen
Empfindlichkeit unserer Augen, die sich leider auch nicht normieren lassen: Das Fundament, auf dem die Bemühungen gestartet
wurden, ist auf Treibsand gebaut - die Protagonisten wollen es nur noch nicht wahrhaben, wo man doch gerade so schön
bastelt . . . mit dem Bath-Interferometer, dessen spektrale Möglichkeiten jener Kreis erst vor kurzem für sich entdeckt hat,
und die Grundlage bildet für diesen Monochromator-Trip.
Unabhängig davon gibt mir der liebe Kurt (der Nickname ist leider nicht geschützt im www ) regelmäßige Rückmeldung:
a) daß er meine Beiträge hier gelesen hat, und b) wie er sie aufgenommen hat. Ist das nicht anständig von ihm?
. . . und um gleiche Verhältnisse zu schaffen: So wie meine Beiträge bei AstroTreff ausgesperrt sind, lieber Kurt, ergeht
es Dir hier auch nicht anders.
############################################################################################################
Der folgende Beitrag wird häufiger überarbeitet.
Zur Systematik der RC_Indexzahl
Erläuterung der RC-Index-Zahl
Die Farbreinheit eines Refraktor-Systems drückt sich im Sekundären Spektrum aus und dem farbabhängigen Öffnungsfehler, Gauß-
fehler genannt. Vor ca. 30 Jahren bewarb Dieter Lichtenknecker seine f/15 Refraktor-Objektive mit einer RC-Indexzahl, die auch
heute noch für eine grobe Klassifizierung in Achromat, Halb-APO und Voll-APO ausreicht. In den letzten Jahren werden aber sehr
lichtstarke Refraktor-Objektive gebaut mit Öffnungen bis zu f/7. Beim Vergleich hochwertiger APO-Triplets vermittelt die
RC_Index-Zahl nicht immer einen richtigen Eindruck, weil der Gaußfehler (in den meisten Fällen) stärker an Bedeutung gewinnt,
ebenso die Anordnung der Schnitt-Weiten des Sekundären Spektrums.
Betrachtet man das Problem aus der Praxis, dann wird bei einer Normal-Empfindlichkeit unserer Augen am Tag von ca. 550 nm
wave auf diese Hauptfarbe Grün "scharf"-gestellt. Die Optik Designer verwenden exakt definierte Wellenlängen, wie sie über
die Fraunhofer Linien im sichtbaren Teil des Spektrums dargestellt werden. Also für
- Hauptfarbe Grün = e-Linie = 546.2 nm wave
- Blau = F-Linie = 486.1 nm wave
- Rot = C-Linie = 656.3 nm wave = H-alpha
- Gelb = d-Linie = 587.6 nm wave
- violett = g-Linie = 435.8 nm wave
- Blau-Grün = 510 nm wave max. Empfindlichkeit der Augen in der Nacht.
Tafel A, Tafel B, Tafel C, Sekundäres Spektrum: Darstellung und Systematik,
Farblängsfehler bei Refraktoren : Schema bei Doublet, Triplet, Super APO
Wenn man also hochwertige Voll-APO's miteinander vergleichen will, dann muß man auf die Hauptfarbe Grün fokussieren und
ein optimal fokussiertes Referenz-Interferogramm erzeugen bei 546.1 nm wave in Form von geraden und parallelen Interferenz-
streifen. Aus dieser unveränderten Fokuslage betrachtet man die Situation für Blau, für 510 nm wave, für Gelb und Rot, und erhält
Interferogramme, in denen der Gaußfehler steckt in Form von Über- oder Unterkorrektur, aber auch der Farblängsfehler in Form
einer Defokussierung oder auch Power genannt.
Aus dem Blickwinkel der Fokuslage für die Hauptfarbe Grün errechnen sich dann Strehl-Werte, die sowohl Farblängsfehler als
auch den Gaußfehler enthalten. Um diese Einzel-Ergebnisse nun mit anderen Refraktoren vergleichen zu können, muß man in
jedem Fall die Fertigungsfehler wie Achskoma und Astigmatismus herausrechnen. Ein Sonderfall tritt ein, wenn man eine System-
Überkorrektur hat, die in der Regel auf falsche Linsen-Abstände zurückzuführen ist. Wegen der Vergleichbarkeit mit anderen
Refraktoren muß also immer die Hauptfarbe bei Grün = 546.1 nm wave liegen.
Eine weitere Besonderheit besteht im unterschiedlichen "Fokus-Shift" zwischen Zwei- und Dreilinsern, wie sie diese Diagramme
zeigen: Doublet, Triplet, Super APO Und nicht zuletzt scheint die Anordnung der Farbschnittweiten selbst noch einen Einfluß
auf den Eindruck der Farbreinheit zu haben. Möglicherweise erscheint die Farbreinheit größer zu sein, wenn Blau vor den Schnitt-
weiten der übrigen Farben liegt und Grün, Gelb und Rot möglichst nahe beieinander liegen.
Aus diesen Einzel-Strehlergebnissen eine wie immer geartete Summen-Zahl in Form einer einzige Polystrehlzahl rechnen zu
wollen, bzw. in Diagrammen darstellen zu wollen, trägt nur zur Verwirrung bei, weil dann unterschieden werden muß zwischen
dem normalen Strehl einer Spektralfarbe und dem neuen Begriff eines "Poly"-Strehls. Eine verbesserte Aussage zur Farbreinheit
erreicht man damit nicht. Das ganze visuelle Farbspektrum interferometrisch abscannen zu wollen in Schritten von 10 nm, würde
die Kosten für Refraktoren in ungeahnte Höhen treiben.
Im Bereich hochwertiger APO's muß also die Systematik um Gaußfehler und Reihenfolge der Farbschnittweiten ergänzt werden,
wenn diese Systematik den hochwertigen APO-Triplets gerechter werden soll. Ein APO kann also einen sehr farbreinen Eindruck
vermitteln, auch wenn die RC_Indexzahl dieses bestimmten APO's nicht so gut ausfallen sollte. Die Qualitäts-Beurteilung am
hohen Strehl-Wert festzumachen ist ebenso einseitig, wie sich im APO-Bereich nur auf die RC-Indexzahl zu fokussieren. Wie bei
vielen anderen Problemen auch, sollte man sich aus unterschiedlichen Blick-winkeln um die Klärung eines Sachverhaltes bemühen.
Liste der Beispiele wird jeweils ergänzt:
Takahashi Super APO TSA 120/900 Jan 2010
Takahashi - TOA 130 / 1000 Gat 07.Febr. 2010
E006A Oberfläche oder Wellenfront messtechnisches Problem
Oberfläche oder Wellenfront ???
5. März 2012
Dem Thema liegt auch ein zweijähriger Streit zugrunde, den ich einstens mit einem Feinoptiger hatte, der viele opt. Flächen herstellte, der demzufolge
seine Meßergebnisse immer auf Oberflächen bezog. Der Streifenabstand eines Interferogrammes beträgt in diesem Fall 1 X Lambda. Werden hingegen
opt. Teleskopsysteme in Autokollimation vor einem Planspiegel im Unendlichen geprüft, dann hat man es mit Wellenfront-Deformation zu tun. Der Streifen-
Abstand eines Interferogrammes beträgt dann 0.5 X Lambda.
Auf diese Anfrage möchte ich deshalb hier antworten:
Quote:
Es geht um die Oberflächengenauigkeit von Spiegeln und Linsen. Die werden üblicherweise ja in Lambda/Wave angegeben. 1/4 Lambda/Wave ist so unterer Standard – es gibt aber auch 1/10 Lambda/Wave Oberflächen und vielleicht mehr.
1) Wie ist es denn, wenn ein Lichtstahl zweimal an so einer Oberfläche reflektiert wird, addieren sich die Fehler auf? Also klassisch beim Newton HS (1/8) und FS (1/8) und raus käme (2/8) = 1/4 Lambda/Wave? Die Literatur sagt ja, Fehler werden addiert. Ist das dann so einfach wie im obigen Beispiel?
2) Wie ist das dann bei einer Linse, bzw. wenn zwei Linsen passiert werden – dennoch wie beim Newton(spiegel)beispiel oben, einfach aufaddieren?
3) Und drittens: Wie verhält sich das bei einem rückseitig verspiegelten Glaselement, z.B. einer Manginlinse, das müsste (wenn das Additionsmodell noch stimmt), ja von vorherein doppelt sein: 1x Linseneintritt und 1x Reflexion an der Verspiegelung.
Ich frage deswegen nach, weil ja bei komplexen optischen Systemen (du weißt ja ich hab einen Klevtsov, gilt ja aber auch für die ACF, EdgeHD u.a.) die Einzelelemente extrem genaue Oberflächen haben müssten, wenn sich die Fehler aufaddieren würden um am Ende noch beugungsbegrenzt zu bleiben. Beim Klevtsov gibt es ja 3 optische Elemente von denen 2 auch noch doppelt durchlaufen werden.
Eine Qualitäts-Angabe, die sich auf eine Oberfläche bezieht, gibt es in der Regel nur bei einer einzelnen Spiegelfläche, als z.B. Kugel- und Parabol-Spiegel,
oder irgendwelche Planspiegel. Diese Qualitäts-Angaben muß man entsprechend umrechnen. L/4 der Oberfläche wäre nur L/2 der Wellenfront,
aus der aber der Strehl berechnet wird. Will man einen Spiegel mit L/10 der Wellenfront, dann muß die Genauigkeit der Oberfläche L/20 betragen.
Bei Pörschke lautete eine Qualitäts-Angabe:Oberflächengenauigkeit λ/8 @ 632.8 nm. Das wären L/4 der Wellenfront @632.8 nm
Test-Anordnungen RoC, Autokollimation, Planflächen, Setup, Parabel-Kompensation
A) Newton-Spiegel werden in der Regel entweder im Krümmungsmittelpunkt vermessen, oder in Kompensation durch/über eine Sphäre. Da wäre der Streifenabstand eines Interferogrammes 1 x Lambda. Gegen einen Planspiegel vermessen, passiert das Licht den Newton-Spiegel 2 x und deswegen ist der Streifenabstand 0.5 x Lambda.
Der Oberflächenfehler von PV L/8 wäre ein Wellenfrontfehler von PV L/4. Die Oberfläche muß also doppelt so genau sein. PV L/8 der Oberfläche eines Spiegels ist also
nur PV L/4 der Wellenfront.
B) Bei einem opt. System, wie es die meisten Teleskope darstellen, interessiert nur die Gesamt-Wellenfront-Deformation, wie sie über ein Interferogramm dargestellt
werden kann. Aus ihr wird dann auch der Strehl-Wert berechnet mit Streifenabstand von 0.5 x Lambda. Gemessen wird die Topografie der Wellenfront, nicht etwa
die Feinstruktur. Angegeben wird der Wert in RMS oder in Strehl. Die Interferenzstreifen kann man als Höhenlinien einer Landschaft auffassen.
C) Bei einer spiegelnden Fläche muß die erforderliche Flächengenauigkeit etwa um den Faktor 4 besser sein, als bei einem Refraktor-System mit brechenden Flächen.
Die "Rauhigkeit" bei einem Refraktor ist deshalb lange nicht so kritisch, wie bei einem Spiegel. Die Rauhigkeit geht nicht in den Strehlwert ein!
Ad 01: Diese Situation gibt es in der Regel nicht - beim Herrig-Schiefspiegler schon. Anders ist es beim Newton-System. Da addieren sich auf der Basis der
Zernike-Koeffizienten die Fehler von Haupt- und Fangspiegel, können sich deshalb auch kompensieren z.B. wenn bei beiden Spiegeln Astigmatismus im Spiel ist. Wer es
ganz genau haben will, müßte den Newton+Fangspiegel vor einem Planspiegel als System vermessen, dabei aber die Koma abziehen, weil ein Newton keine Koma auf der
Achse hat. Die Additions-Rechnung in Frage 1. ist deshalb falsch, weil sie nicht die Art der Deformation der einzelnen Fläche berücksichtigt.
Ad 02: Bei jedem Refraktor-Objektiv werden bis zu 8 Flächen vom Licht passiert, in Autokollimation über einen Planspiegel sind es dann 16 + 1 Flächen. Eine Addition
der Oberflächenfehler wäre nur auf der Basis der Zernike-Koeffizienten möglich wegen der kompensatorischen Wirkung einzelner Flächen zueinander. In der Regel
vermißt man jedoch nur das Gesamt-Objektiv, weil ein Teil der Wellenfront-Fehler (wie Spherical, Astigmatismus etc.) gar nichts mit der Oberfläche der Linsen zu
tun hat, sondern mit den Abständen, der Fassung etc. Wenn ein RC-System überkorrigiert reagiert, dann stimmt in der Regel der Spiegelabstand nicht. Bei Linsen
ist das ähnlich.
Ad 03: Bei einem Mangin-Spiegel bekäme das Licht 2x den Fehler der brechenden Linsenfläche aufgedrückt und 1x den Fehler der reflektierenden Spiegelfläche.
Dabei ist die reflektierende Fläche sehr viel anspruchsvoller, als die brechende Linsenfläche. Trotzdem wird in einem solchen Fall immer das Gesamt-System
in seiner Genauigkeit bewertet und beworben, und das kann bedeuten, daß sich einzelne Flächen gegenseitig kompensieren. Dafür gibt es dann auch Asphären,
wie es die Kegelschnittflächen darstellen, oder Flächen höherer Ordnung, wie z.B. eine Schmidtplatte. Und das wird dann auf Null retouchiert. Das heißt:
Man stellt die Einzelflächen auf das normale Maß her, setzt das System zusammen, und retouchiert dann die Fehler an eine der Teilflächen auf Null.
Ein Beispiel:
Das folgende Interferogramm könnte auf mehrere Arten entstanden sein:
a) ein Refraktor-Objektiv vor einem Planspiegel im doppelten Durchgang: Streifenabstand = PV L/2
b) Ein Kugelspiegel im Krümmungsmittelpunkt im einfachen Durchgang: Streifenabstand = PV 1 x Lambda
c) Ein Parabolspiegel in Kompensation im einfachen Durchgang: Streifenabstand = PV 1 x Lambda

Bei folgendem Beispiel sieh man in der Mitte eine Obstruktion. Das kann sein
a) Ein Newton-Spiegel in Autokollimation, die Abstruktion ist der Fangspiegel oder die Bohrung vom Planspiegel
b) Irgend ein katadioptrisches System, SC, RC u.ä.
c) eine simulierte Obstruktion
Der Streifenabstand ist in allen Fällen PV 0.5 x Lambda

E017 Strehlwert und Obstruktion - Modulationsübertragungsfunktion
Modulationsübertragungsfunktion
http://www.epsilon-lyrae.de/Seeing/MTF1/ArtikelMTF1.html
http://de.wikipedia.org/wiki/Modulations%C3%BCbertragungsfunktion
Ein visueller Stern-Interferometer im Eigenbau SuW 4/99
http://rohr.aiax.de/SuW_Eigen_Inter.pdf
Lieber Matthias,
herzlich willkommen hier in der Astro-Fan-Gemeinde. Laß mich zu folgender Frage mit einer synthetischen Simulation
antworten, die man leicht an einem künstlichen Sternhimmel wiederholen kann.
Quote:
Nur zu meinem Verständnis: Wie wirkt sich die höhere Obstruktion von z.B. 45% eines F4 Newtons fotografisch
gegenüber einem Newton mit 30% aus ? Ist das überhaupt merkbar und wenn doch, wo würde ich den Kontrastverlust
bei der Fotografie mit z.B. einer DSLR eher merken: unter guten Bedingungen oder schlechten? Ist jemand so Nett und
erklärt das einem ohne sich in optischen/technischen Details zu verlieren?
Für mein Auswertprogramm AtmosFringe, das vor allem die Obstruktion berücksichtigt bei der Point Spread Function
oder EnergieVerteilungsFunktion habe ich ein Interferogramm derart erstellt, daß der Durchmesser des künstlichen
Interferogrammes 100 Einheit sind, und sich die Obstruktion von 20%, 40%, 60% bis 80% steigern läßt. Nun entsteht
die Frage, was da im Einzelnen passiert? (Der 100% rote Umkreis ist erkennbar, ebenso die grauen Obstruktions-Kreise.
Die horizontalen schwarzen Linien stellen die Interferenz-Streifen dar.

In der Wellenfront-Darstellung ändert sich zwar an den Flächenfehlern nichts, aber sie werden über die Obstruktion
sukzessive ausgeblendet, sodaß der von der Rest-Fläche ermittelte Strehl-Wert leicht variiert von Strehl = 0.996 bis
0.993.
Was man nun sehr gut erkennt, wie sich über den Einfluß der Obstruktion die Lichtenergie vom Maximum allmählich in
die Beugungsringe verlagert und damit ein Sternscheibchen vom Durchmesser her größer wird bei einem obstruierten
System. Im Maximum steckt also weniger Energie. Mit der Strehl-Definition hat das erst einmal gar nichts zu tun.
Nun kommen aber die ganz Verwegenen, und versuchen das Strehl-mäßig gegeneinander aufzurechnen.
Nach dem Motto, man müsse doch die Obstruktion strehl-mäßig abziehen. Für den Strehl zählt aber wirklich
nur die Fläche, die von der Optik benutzt wird: Bei einem obstruierten System zählt also definitionsgemäß die
obstruierte Fläche nicht: Weshalb soll ich mit etwas vergleichen, was nicht vorhanden ist. Trotzdem wird
man bei visueller Nutzung eines Newtons einen möglichst kleinen Fangspiegel wählen und bei fotografischer
Nutzung die Vignettierung im Auge haben. Zwischen diesen beiden Anwendungen bewegt sich die Diskussion
um die Obstruktion.

Es gibt noch eine praxis-nähere Möglichkeit, diesen Sachverhalt darzustellen. Im Krümmungsmittelpunkt ist ein Kugel-
spiegel die Idealform eines nicht obstruierten Systems und bei meinem künstlichen Sternhimmel mit Pinhole zwischen
3-5 Micron ergäbe das feine nadelscharfe Pünktchen. Ein solcher Kugelspiegel läßt sich leicht über Scheiben aus Ton
papier wie im oberen Verfahren abblenden. Und man würde erleben, wie sich die Lichtenergie vom Maximum allmählich
in die Beugungs-Ringe verlagert.
Bei der MTF-Kurve aber bekommt man einen Bereich, der sich für die KontrastÜbertragung sogar positive auswirkt.
http://de.wikipedia.org/wiki/Modulations%C3%BCbertragungsfunktion
für die volle Auflösung bitte das Bild anklicken: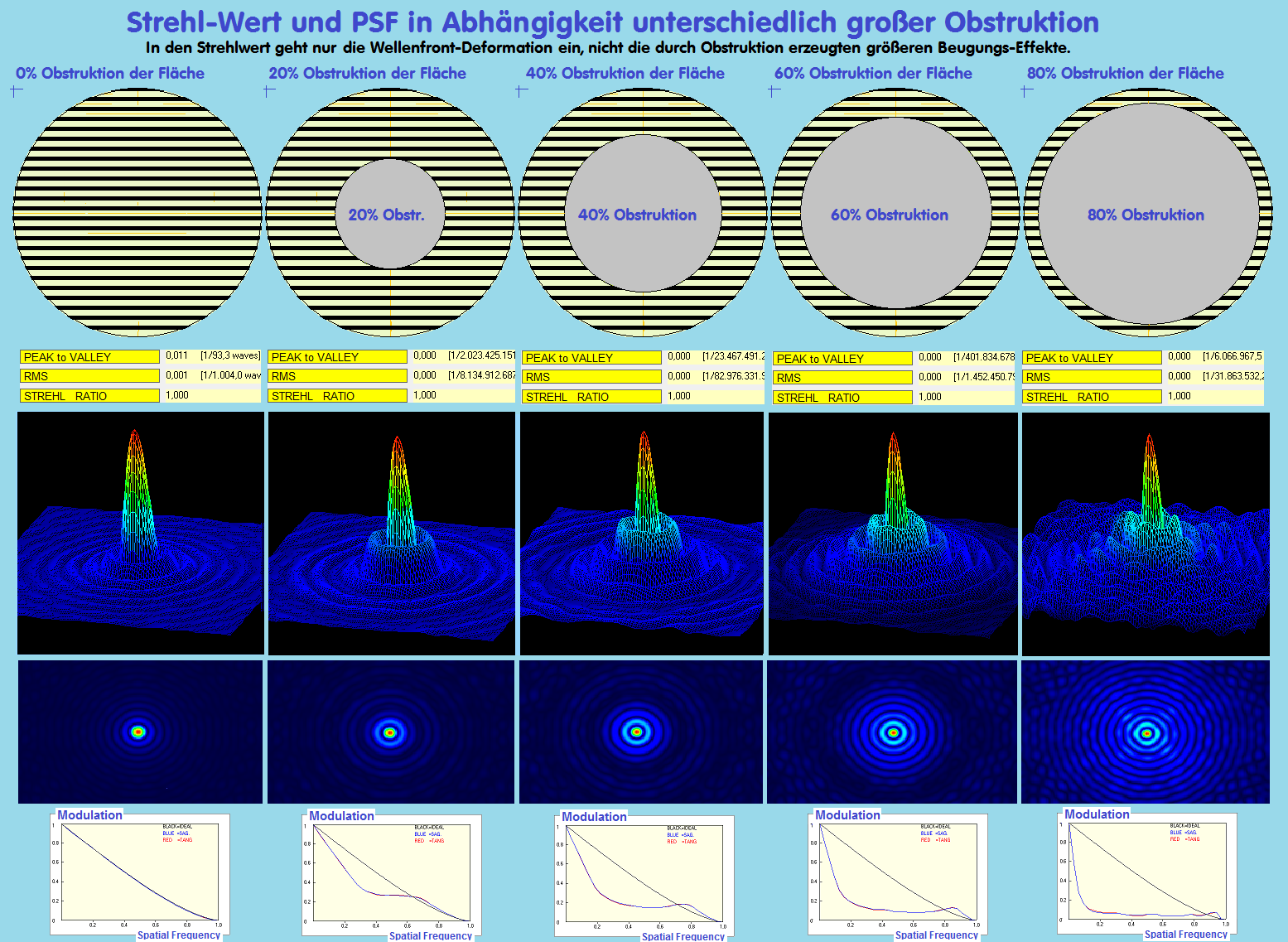
Im Falle eines drei-eckigen Astigmatismus schaut die Energie-Verteilung dann so aus:
Mit diesem Newtonspiegel 450 mm Durchmesser f/4.5 wurde diese Aufnahme gemacht. Bei einem Vergleich mit anderen
Aufnahmen aus dem Web schneidet diese Aufnahme gar nicht so schlecht ab. http://www.harpoint-observatory.com/galerie/galaxien/ngc891.jpg

Eine Aufnahme aus dem Internet - groß ist der Unterschied nicht.

Nochmals die praktische Demonstration, was Obstruktion bei der Abbildung von winzigen Pinholes (3µ-5µ) bei einem ca.
L/10 PV wellenfront Kugelspiegel passiert: Je größer die Obstruktion, umso mehr verlagert sich die Lichtenergie in die
Beugungs-Ringe, wie bereits oben über die PSF simuliert.

Viele Spiegel sind mehr oder weniger astigmatisch, also habe ich meinen Kugelspiegel um ca. 1 Lambda PV verspannt,
wie man an den Ergebnissen sieht. (Man sieht beim Spiegel die seitlichen Klammern, die eine Spannfeder auf der Rück-
seite halten. So ziehen diese Spannfedern den Spiegel bei 09:00 Uhr und 03:00 Uhr nach hinten, ganz so, wie es die
Wellenfront-Darstellung zeigt.

Beim Astigmatismus 1. Ordnung bekommt man im Fokus ein wunderbares Kreuz. Bei einer Obstruktion verlagert sich
erneut die Energie in die Beugungsringe, allerdings kreuzförmig. Ein dreieckiger Astigmatismus verschmiert sich in
diesem Fall besser.

E035 HOTECH Zentrierung von SC-Systemen
Hotech Laser Collimator
Auf dem ITV 2013, "Vatertag der alten Säcke" wurde von Andreas Pietsch diese Zentriermöglichkeit für katadioptrische Teleskope vorgestellt, also
optische Systeme, die aus einem Haupt- und Sekundärspiegel bestehen und zusätzlich mit einer Schmidtplatte bzw. einer Meniskus-Linse bestückt
sind, wie es im untersten Bild auf der Internetseite dargestellt ist: http://www.hotechusa.com/category-s/23.htm
Wer also über keinen großen Planspiegel verfügt und ebenso keinen künstlichen Stern hat, den er in den Okular-Auszug stecken kann, der muß
entweder sein Schmidt-Cassegrain, Maksutov etc. am Himmel zentrieren (Polarstern), oder aber er legt sich dieses System zu, mit dem er ebenfalls
erfolgreich den Sekundär-Spiegel dieses Systems zentrieren kann: Dabei läßt aber bereits der YouTube-Film erkennen:
http://www.youtube.com/watch?v=ZNzBEqe5FlE , daß es sich in Wirklichkeit nur um die Zentrierung des Sekundärspiegels handelt. Der Hauptspiegel
müßte nach einem anderen Verfahren zentriert werden, was aber weniger oft der Fall ist. Auch für diese Art der Zentrierung ist ein wenig Übung
und opt. Fachwissen erforderlich. Siehe auch: http://www.youtube.com/watch?v=YanAqpo9ddQ&lr=1&uid=KYMiW3ew7ZdPLZ55wzGDeQ
Der Hotech Laser Collimator soll also in seiner Funktion dargestellt werden ohne die überflüssige Diskussion, wieviel besser andere Zentrier-Methoden sein mögen.
Je nach persönlicher Ausrüstung und Erfahrung gibt es mehrere Wege, Zit: "All CT, SCT, Makustov, & RC" zu zentrieren, wie es die Werbung im Link verspricht.
Warum ich allerdings die Einschränkung auf die Sekundär-Spiegel-Zentrierung mache, erkläre ich später.
Zunächst erscheint beim Auspacken eine "Schieß-Scheibe", in deren Zentrum ein Kreuz-Laser eingebaut ist und im vorletzten Ring auf 120° jeweils ein Punkt-Laser.
Über einen Schalter oben lassen sich diese verschiedenen Laser unterschiedlich einschalten.

Besser erklärt die Rückseite dieses Tablets (Bayerisch "Taferl") die Anordnung. Die Batterie unten muß mit dem Plus-Pol zum Betrachter eingelegt werden.
.

Eine wesentliche Einheit bildet dieser teildurchlässige kleine Planspiegel, der in die 2" Okular-Steckhülse eingesetzt wird und die drei Punkt-Laser im Fokus des
SC-Systems so zurückreflektiert wird, daß es im Ideal-Fall zum analogen Kreisring der "Schieß-Scheibe" wieder zu sehen ist, jeweils um 180° gedreht aus opt.
Gründen. Da dieser kleine Flat teildurchlässig verspiegelt ist, kann man von der Rückseite hinter dem Okularauszug den zentrischen Verlauf beim zusätzlichen
Einschalten der drei Punktlaser kontrollieren. Hier taucht aber zugleich das mechanische Problem auf, daß es immer ein Spiel zwischen Hülse und Spiegel-
Halterung von 0.1 - 0.2 mm gibt, sodaß das Festziehen der Hülsenschrauben bereits zu einer Verkippung dieses kleinen Spiegels führen kann, sodaß es besser ist,
diese Einheit lediglich einzulegen, aber nicht festzuschrauben bei horizontaler Test-Anordnung.
.

http://www.youtube.com/watch?v=ZNzBEqe5FlE Bereits die Anleitung auf YouTube zeigt, daß man das "Taferl" bzw. den HOTECH möglichst so aufstellt, daß der
Abstand zum Teleskop dort zu liegen hat, wo der Krümmungsmittelpunkt des Hauptspiegels liegt. Der Kreuzlaser wird dann als kleiner Kreis mit den vier Kreuz-
balken abgebildet, die man durch Verkippung zentrisch auf die Schießscheibe zentriert. Zuvor muß aber auch die Kreuzlaser-Figur zentrisch auf der Fangspiegel-
Einheit zu sehen sein, und später auch zentrisch auf der Rückseite der Hilfsspiegel-Einheit im Okular-Auszug.
.

Der "Prüfling" in Autokollimations-Anordnung: Zunächst wird nach einer Autokollimations-Testanordnung das C 9.25 vor einem 400 mm Planspiegel zentriert. Dazu braucht
man einen künstlichen Stern exakt auf der opt. Achse, wie man drei Bilder weiter sehen kann. Prinzipiell wird durch diesen Aufbau der Blick zum Himmel mit doppelter
Genauigkeit dargestellt. Diese Testanordnung zentriert sich in zwingender Weise selbst, weil man den künstlichen Stern erst sieht, wenn das System zum Kollimations-
Planspiegel exakt zentriert ist. Links im Bild also das C 9.25, rechts der Planspiegel.
.

Die gleiche Testanordnung mit einem 500-mm Zeiss Werkstatt-Planspiegel.
.

.
Die Einheit "künstlicher Stern" auf der opt. Achse, die in den Okular-Auszug gesteckt wird. Das Lichtleiter-Kabel leitet das Licht hinter die Pinhole aus Gründen
der Wärme, die die Lichtquelle erzeugt. Diese Wärme würde den Test-Vorgang empfindlich stören.

.
http://de.wikipedia.org/wiki/Sim%C3%A9on_Denis_Poisson Quote:
Poisson war ein Schüler von Pierre Simon Laplace und beschäftigte sich mit den physikalischen Grundlagen von Wellen, arbeitete über Akustik, Elastizität und Wärme sowie über die elektrischen Eigenschaften von festen Körpern. 1812 publiziert er eine Erweiterung der Laplace-Gleichung um die Oberflächenladung. 1818 sagte er den Poisson-Fleck voraus, wenn Licht Wellencharakter haben sollte. Dies bezweifelte er allerdings. Er führte heftige Diskussionen mit Christiaan Huygens als Verfechter der Wellentheorie des Lichts. Der Disput wurde durch den experimentellen Nachweis des Flecks durch François Arago beendet.[2] 1838 veröffentlichte er seine Wahrscheinlichkeitstheorie. Darin enthalten war die Herleitung der Poisson-Verteilung.
Die folgende Zentrierung am Stern benutzt den sog. Poisson-Punkt eines obstruierten Systems, was im 19.-Jahrhundert als Beweis für die Wellennatur des Lichts
angeführt worden war, siehe das Zitat aus Wikipedia. Dieser Punkt muß konzentrisch im defokussierten Sternscheibchen - bei hoher Vergrößerung - zu sehen sein.
Zuvor hatte ich also nach dieser Methode das C 9.25 zentriert und festgestellt, daß das C 9.25 sich in der Zwischenzeit offenbar etwas verstellt hatte: Der Poisson-
Punkt sitzt also nicht ganz zentrisch mittig in der "Figur", Bild links. Mit dem Bruchteil einer Drehbewegung an der analogen Zentrierschraube vorne an der Sekundär-
Spielgel-Einheit kann man das korrigieren.

Und hier die Begründung, warum "Bob Knobs" für diesen Fall sehr, sehr unpraktisch sind: An meinen Schrauben-Dreher ist ein Zeiger angebracht, damit ein Winkel-
Schritt von 1-3° noch erkennbar ist. Mehr ist für diese Korrektur oben gar nicht erforderlich. Unter hoher Vergrößerung bei ca. 1000-fach läßt sich das gut
kontrollieren.
.

Mit diesem perfekt zentrierten System sollte auch bei der HOTECH-Zentrier-Einheit ein gleiches Ergebnis herauskommen. In Beantwortung der weiter unten
folgenden Fragen nun der Verlauf der detaillierten Zentrierung:
Das Hotech-Tablet kann in den 3 Raumachsen verstellt und geneigt werden - eine ganz wichtige Voraussetzung bei der Einrichtung des gesamten Aufbaues
zusammen mit dem C 9.25, wie auf dem nächsten Bild zu sehen. Auch das C 9.25 kann ebenfalls - für alle Fälle - verstellt und geneigt werden.
01. Man schaltet also nur den mittigen Kreulaser ein und sucht zunächst den richtigen Abstand zum Hauptspiegels des C 9.25. Dieser zeigt sich dadurch, weil
das Reflex-Bild des Kreuzlasers, den der C 9.25 auf dem Hotech Tablet erzeugt in seiner Größe variiert, also bei richtigem Abstand auch nur als Punkt zu
sehen ist und kurz davor als Kreuzlaser mit Ring, der zu "Schieß-Scheibe" zentrisch sein sollte. Wenn dabei das Bild auf der C 9.25 Fangspiegel-Einheit sich
verschoben hat, so sieht man das auch auf dem Tablet als dezentrierten Reflex. Solange jedoch nur der Kreuzlaser eingeschaltet bleibt, wird man hinten im
Okular-Auszug nichts erkennen können, schon von der Logik her nicht, weil der Strahlengang des Kreuzlasers nur den Hauptspiegel erreicht, nicht jedoch das
ganze System. Das ändert sich erst, wenn man die 3 parallelen Punkt-Laser dazu-schaltet. Jetzt ergibt sich hinter dem kleinen teilverspiegelten Hilfs-Planspiegel
ein Fokus-Bild, abhängig davon, wo dieser Spiegel im Fokus steht.
02. Mit dem Kreuzlaser kann man genaugenommen nur den richtigen Abstand des Tablets zum C 9.25-Prüfling einstellen und in etwa die Höhe zur opt. Achse
beider Komponenten im Test-Aufbau. Man sollte sich unbedingt auch die oben angegebenen YouTube-Videos anschauen, damit man den Vorgang besser
nachvollziehen kann.
.

Erst nach dem Zuschalten der 3 Punkt-Laser, die prinzipiell ein paralleles Strahlen-Bündel aus dem Unendlichen darstellen, entsteht rückseitig im OAZ dieser Licht-
Fleck, der am Genauesten anzeigt, daß nun das System beiderseits zusammen auf der opt. Achse ist: Man wird also des öfteren die Komponenten feinzentrieren
müssen.
.

Entscheidend aber im 3. Vorgang ist die nächste Abbildung: Aus opt. Gründen entsteht wie bei jedem anderen Testaufbau ebenfalls ein seiten-verkehrtes auf dem
Kopf stehendes Bild, was mit den 3 Reflex-Punkten wahrgenommen wird. Einzige Bedingung: Diese Punkte müssen auf dem Kreisring liegen, auf dem auch die
Punkt-Laser ihren Ausgang genommen haben. Eine Verschiebung korrigiert man im YouTube-Film mit Hilfe der Bob Knobs.
.

.
Kritisch in diesem Zusammenhang ist, wie oben bereits erwähnt, das mechanische Spiel der Hotech-Okular-Spiegeleinheit mit dem 2" Okular-Auszug des C 9.25.
Innerhalb dieses Spiel kann man diese Laserpunkte "wandern" lassen. Es müßte deshalb eine Passung sein mit möglichst wenigen hundertstel Millimeter Spiel.
Bereits das Anziehen der Stellschrauben verändert die Lage der Punkte.

.
@ GSO RC 8-inch optisches Zentrierverfahren für Hauptspiegel sehr genau !
Neues GSO 8" f/8 RC - Ritchey-Crétien 203/1624 ___ Hauptspiegel-Zentrierung beim Cassegrain-System Abrollverfahren
@ GSO 8" RC - Hauptspiegel-Zentrierung über Laser-Beam Laser Pointer, für Andi 8-inch GSO RC Abrollverfahren
GSO 8" RC 203/1624 Auf die Spitze getrieben Hauptspiegel Restastigmatismus eliminieren
.
Wie man aus den Links ersehen kann, muß bei manchen Systemen auch der Hauptspiegel zentriert werden. Bei einem RC-System (GSO-RC) würde ein
dezentrierter Hauptspiegel Astigmatismus erzeugen. (Eine andere Ursache für Astigmatismus im System wäre die Hauptspiegel-Lagerung selbst: Bei
manchen SC-Systemen und Maksutovs.) Die unterschiedlichen Möglichkeiten der Hauptspiegel-Zentrierung ist in den oberen Links dargestellt, entweder
als Abroll-Verfahren, oder im Krümmungsmittelpunkt des Hauptspiegels im Zusammenhang mit der opt. Achse. Auch über die Astigmatismus-Figur
könnte man den Astigmatismus des Hauptspiegels bei Dezentrierung desselben eliminieren. Prinzipiell läßt sich der Hotech Laser Collimator für die
Fangspiegel-Zentrierung verwenden. Die Anschaffung dieser Einheit entspricht in etwa einem hochwertigen Ethos-Okular.
Nachtrag:
Ein paar erklärende Zeichnungen aus dem YouTube-Film:
Der Cross Hair / Kreuz-Laser wird nur zu Zentrierung des Test-Aufbaus benutzt. Sein Licht erreicht wegen der Obstruktion des Sekundär-Spiegels den Hauptspiegel nicht.
In diesem Fall sieht man im Okularauszug keinerlei Licht-Reflex.

Der Hauptspiegel reflektiert nur den Kreuzlaser auf die "Schieß-Scheibe" zurück, abhängig vom Abstand, den diese vom Hauptspiegel selbst hat. Vorteilhaft ist
in der Nähe des Krümmungsmittelpunktes vom Hauptspiegel.

Erst wenn man die drei äußeren parallelen Punkt-Laser dazuschaltet, die das parallele Strahlen-Bündel simlieren sollen, durchlaufen dieses stellvertretend für
ein Bündel mit dem vollen Durchmesser das opt. System bis zum Planspiegel im Okular-Auszug und werden dort reflektiert und auf die "Schieß-Scheibe"
zurück-reflektiert, je nach Justier-Zustand des Systems. Eine Kontrolle, ob der kleine Planspiegel wirklich eine Total-Reflexion auf der opt. Achse ermöglicht,
gibt es leider nicht, weil die Okular-Auszug-Hülse dafür zu viel Spiel hat. Hier hilft nur der Sterntest am großen Planspiegel weiter, mit dem man auch einen
möglichen Astigmatismus erkennen kann.

Beantwortung der Frage in Beitrag #11 von Volker:
Überprüfung der Kollimation von HOTECH Laser Collimator
Wer der Technik dieses HOTECH Laser Collimator mißtraut, hat eine einfache Möglichkeit, dies zu überprüfen:
Im Abstand von 1.5 - 2.0 Meter stellt man die Komponenten zueinander orientiert auf. Links der HOTECH Laser Collimator, rechts ein 20 cm Zeiss Planspiegel.
.

.
Im eingeschalteten Modus schickt der HOTECH Laser Collimator (HLC) vier Bündel zum Flat: mittig den Kreuzlaser und außen je einen Punktlaser, die alle
zueinander räumlich pparallel sein müssen. Der besseren Sichtbarkeit wegen zunächst die Projektion auf eine weiße Fläche.

Jetzt auf dem Flat zu sehen, der aber die vier Bündel in sich total-reflektiert und zum HLC zurückschickt.
.

.
und wie erwartet, landen alle Bündel wieder dort, wo sie eigentlich landen müssen: Das Laser-Kreuz auf dem Kreuz der "Schieß-Scheibe", die drei Punktlaser dort,
wo sie hergekommen sind. Der Kollimator ist technisch also in Ordnung.

.
.
E074 Wider alle opt. Vernunft - Petzval-Systeme Abstand Objektiv - Reducer einhalten
Wider alle opt. Vernunft - Petzval-Systeme
Petzval Systeme sind fotografische Systeme. Als solche bieten sie a) ein ebenes Bildfeld und b) eine
punktförmige Abbildung bis zum Bildfeld-Rand. Petzval-Systeme bestehen prinzipiell aus einer
Linsengruppe am Eingang eines Teleskops und in Okular-Nähe ebenfalls ein zweites Element, eine
Art Feldkorrektor. Der Abstand der ersten und zweiten Linsengruppe ist vom Design festgelegt, also
nicht variabel, "ein-betoniert" gewissermaßen. Ein solches System erzeugt also ein ebenes Bildfeld
mit einer perfekten Abbildung bis zum Rand, und die Okular-Einheit mit Fokussierung erfolgt * NACH *
dem eigentlichen Petzval-System. So sind alle die Teleskope gebaut, die man z.B. als Takahashi FSQ
85 ED, als TeleVue 140 oder als Pentax 75 SDHF kaufen kann oder konnte. Bis zum Okular-Auszug
sind es also "starre" Systeme mit festen Abständen. Mit dem Okular-Auszug wird auf ein solches
System fokussiert.
Beispiele Für Petzval-Systeme:
http://www.astro-foren.de/showthread.php?15498-Ausgesprochen-farbrein (erster Bericht)
http://www.astro-foren.de/showthread.php?14448-quot-Foto-Maschine-quot-TeleVue-140-APO-Petzval-System
http://www.astro-foren.de/showthread.php?10322-Takahashi-FSQ-85-ED&p=39150#post39150
http://www.astro-foren.de/showthread.php?9386-Pentax-75-SDHF-von-Thomas-(Knickohr)&p=35817#post35817

Seit einiger Zeit gibt es für lichtstarke Teleskope, sei es APO's oder Halb-APO's sogenannte Flattners oder Reducers, die zusammen
mit dem vorderen Objektiv ein ebenes Bildfeld und eine gute bis perfekte punktförmige Abbildung garantieren, wenn
ja, wenn der ! richtige ! Abstand zwischen Objektiv und Flattner eingehalten wird.
Und nun beginnt das Drama: Dieser Flattner braucht - so erzwingt es sowohl Objektiv wie Flattner zusammen als Einheit - braucht also
einen festen Abstand zueinander, den man auf der opt. Bank ausmessen kann, und auf der Skala des Okular-Auszuges angeben kann.
In diesem Fall sollte eigentlich der Okular-Auszug mit dem feststehenden/ermittelten Abstand festgeklemmt werden, weil die
Fokussierung auf ein solches Bild nach der Einheit Objektiv+Flattner erfolgen sollte. Das verstehen aber offenbar nicht alle, und nun
nimmt das "Unglück" seinen Lauf. Und weil bei falschem Abstand aus den Sternpünktchen plötzlich kleine Striche werden
können, wird eine Verkippung von Bildfeld zu Chip-Ebene diagnostiziert und darüber hinaus noch ein Kipp-System
angepriesen. Genau solche Striche sehe ich aber auch, wenn der Abstand zwischen Objektiv zu Flattner falsch ist.
Also habe ich zusätzlich im 1. Bericht auch die Abstände veröffentlicht. http://rohr.aiax.de/APM-107_13.jpg
Der Sternfreund hat sich also für dieses System entschieden. Hat sich den optimalen Abstand zwischen Objektiv und Flattner/Reducer
ausmessen lassen, hat die richtige Skala-Einstellung gezeigt bekommen. Auch der Backfokus wurde ausgemessen und über den
Artificial Sky Test entstanden Bilder zur Abbildung im Bildfeld - alles wunderbar.
In der Folge stimmte aber die Sache dann doch nicht. Warum eigentlich? Also wurde ihm noch eine Kipp-Einrichtung verkauft, weil es
daran liegen könnte. Jetzt funktionierte es erst recht nicht. Ja, warum denn nicht?
Die einfache Regel heißt: Der Abstand zwischen Objektiv und Reducer muß in jedem Fall eingehalten werden. Das heißt, wenn man
erfolgreich fokussiert hat, bzw. "scharf" gestellt hat, dann muß die Skala-Einstellung 100-Einheiten anzeigen. Widrigenfalls unbefrie-
digende Ergebnisse herauskommen. Das bedeutet, daß man über Abstands-Ringe zwischen Reducer und Kamera-Chip den Abstand
so einstellt, daß man bei erfolgter Fokussierung bei der Skala-Einstellung 100 Einheiten gelandet ist. Dafür war u.a. mein 1. Bericht
gedacht: mit folgendem Hinweis.
Quote:
Zusammen mit dem 0.75 Flattner die Strehl-Qualität auf der opt. Achse, wobei man unbedingt den richtigen Abstand, Objektiv zu 0.75 Flattner, von 100 Einheit auf
der Skala einhalten muß. Würde dieser Wert nicht stimmen, bekommt man Koma-Figuren und man kann nicht mehr scharfstellen. Außerdem geht dann in
das Meßergebnis eine leichte Dezentrierung des Flattners ein, das man aber erst merkt, wenn der Flattner zu nahe am Objektiv sitzt. Hier wird der
Flattner "überstrapaziert". Für diesen Fall würde auch die Korrektur nicht funktionieren. Man kann also das System sehr schnell falsch beurteilen, wenn
man die richtigen Abstände nicht einhält.
Die opt. Bauteile können also noch so gut sein. Wenn Grundregeln der Optik nicht eingehalten werden, dann funktioniert
es leider nicht. Die Fokussierung an der falschen Stelle verführt dazu regelrecht.
----------------------------------
Wie finde ich den optimalen Abstand Objektiv - Flattner (Reducer) ?
Damit ein opt. System die gewünschten Bedingungen erfüllt, müssen z.B. die Abstände der einzelnen Bauteile eingehalten werden.
Bei einem Petzval-System wird das erzwungen, vorderes Objektiv und hinterere Feldkorrektur-Linse haben einen festen abstand, und
erst danach regelt der OAZ-Fokuser den Abstand des Systems zum Fokus. Der eigentlich übliche Fall erzeugt deshalb keine Probleme.
Nun gibt es seit einiger Zeit die Flattner und Reducer. Und auch hier müssen die richtigen Abstände eingehalten werden, wenn das
System funktionieren soll. Sinniger-weise ist für ein solches Gesamt-System der OAZ-Fokuser genau an der falschen Stelle, also zwischen
vorderer Objektiv-Linse und 2. LinsenGruppe. (Und nun fokussieren sich die "braven" Astrofotografen einen "Wolf" und ärgern sich
über die schlechten Ergebnisse, weil ihnen keiner sagt, daß das so nicht funktionieren kann.)
Wenn ich für eine solche Situation den richtigen Abstand ermittle, am Beispiel dieses SkyWatcher Esprit, dann verkippe ich zunächst
das Gesamtsystem (Refraktor+Reducer) in seine maximal-Position vor dem Planspiegel, also 1.5° Kippwinkel, was ca. 55 mm Bild-
felddurchmesser ergibt. In dieser Stellung müssen die Sternpünktchen möglichst genauso gut abgebildet sein, wie auf der opt. Achse.
Also schiebe ich den OAZ zusammen mit dem Reducer solange "rein" und "raus", bis die Stern-Abbildung möglichst punktförmig erfolgt.
Nun bekomme ich regelmäßig zwei Abstände:
a) den Abstand auf der OAZ-Skala, den ich angebe, und der bis zuu +/- 1 mm eingehalten werden sollte.
b) auch messe ich den Abstand von der letzten Flattner-Fläche ohne Gewinde zum Fokus aus.
Der Stefan hat sich an die beiden Abstände gehalten und damit die folgenden Aufnahmen gemacht: M3 mit DSLR
Wenn also die richtige Position auf der OAZ-Skala eingestellt ist, dann muß das Bild auf dem Kamera-Sensor "scharf" sein. Dann darf man eben NICHT mehr
mit dem OAZ-Fokuser fokussieren wollen.
Und hier ist die Kipp-Vorrichtung zur kontrollierten Verkippung der Refraktoren vor einem Planspiegel. Das ginge auch am Himmel, wenn man einen Stern an
den Bildfeldrand stellt: Da müßte man aber dann zwei Fokussierer haben: einen zwischen den Linsen und einen zwischen Flattner und Fokus-Chip.
E006 Der Unfug mit dem Polychromatischen Strehl
Einleitung
Den auf Astrotreff und A.de unter großem zeitlichen Druck veröffentlichten Messungen zum oberen
Begriff fehlt die logische Systematik und vermittelt lediglich den Eindruck von Aktionismus. Der Takahashi-
Link funktioniert nicht mehr(siehe deshalb unten), lediglich die zwei TMB-Tabellen sind verfügbar als
einizge Legitimation, die Szene mit "neuen Erkenntnissen" zu beglücken. Dort findet man nur Einzelstrehls,
nicht jedoch einen PolyStrehl als Zahl oder Diagramm. Der Ursprung solcher Diagramme stammt somit ein-
deutig aus optical Design Programmen. Ein seriöser Vergleich scheitert also bereits an der geringen Zahl
der Veröffentlichungen selbst und deren Vergleichbarkeit.Vor einer ernstzunehmenden Diskussion müßten
daher u.a. folgende Fragen einvernehmlich geklärt werden:
Quote:
- das über ein Optical Design Programm gewonnene Polystrehl-Diagramm ist eine idealisierte Darstellung und damit etwas
völlig anderes, als ein aus meßtechnischen Ergebnissen gewonnenes Diagramm, welches das aktuelle Objektiv repräsentiert.
- bei einem meßtechnisch gewonnenen "Poystrehl-Diagramm" müssen zuallererst die Beurteilungs-Kriterien geklärt werden,
bevor man unterschiedliche APO's oder Halb-APO's miteinander vergleichen könnte. Prinzipiell vergleicht man opt. Systeme und
nicht deren Fertigungsfehler. Es ist ein Desig-Problem und kein meßtechnisches.
- ungeklärt ist beispielsweise der Umfang des zu untersuchenden Spektrums, wieviel Meßpunkte mit welcher Linie dazustellen sind
- wie sind z.B. Fertigungsfehler zu behandeln (Astigm, Koma und Spherical) und müssen diese, um der Vergleichbarkeit willen zu anderen
Objektiven, deaktiviert werden oder nicht, analog der Situation beim Design.
- für welchen Objektiv-Bereich bzw. welche Öffnungszahl ist ein zusätzlicher selektiver Polychromatischer Strehl sinnvoll
- die Frage der Gewichtung einzelner Spektral-Bereiche ist nicht verbindlich geklärt besonders hinsichtlich der Nutzung der Optik.
- ob die PolyStrehl-Kurve aus der Position des Fokus-Punktes der Hauptfarbe dargestellt werden soll, oder ob die Strehl-Kurve den
Strehlwert jedes einzelnen Meßpunktes des Spektralbereiches darstellen soll. Das wären dann zwei Polystrehl-Kurven, zusätzlich
einer unsinnigen Diskussion darüber.
- gibt es eine klare Übereinkunft bzw. Begrenzung, wo eine PolyStrehl-Kurve sinnvoll bzw. sinnlos ist.
- gibt es ernstzunehmende Quellen als Beleg, daß dieser Begriff Eingang gefunden hätte in die Meßtechnik bzw. in Test Reports.
Nur weil ein Hobby Optik-Designer glaubt, seine idealisierte Sichtweise auf einen praxis-orientierten Meßbereich übertragen
zu müssen, mit dem Versuch eine Foren-Diskussion zu majorisieren, wird ein "meßtechnischer Polystrehl" ja nicht informativer.
Es steht die Diagramm-Verliebtheit einiger Theoretiker gegen den Informations-Wert und Arbeitsaufwand in der Meßpraxis.
In die Poly-Strehl-Diagramm-Übersicht fließen (ohne die Fertigungsfehler) der Farblängsfehler/Defokussierung ein
und der Gaußfehler/Farbabhänger Öffnungsfehler. Bezugs-Punkt ist in der Regel die Hauptfarbe Grün = e-Linie, die
Strehlabweichung erklärt deshalb die Defokussierung zu Grün und bezieht zugleich noch den Gaußfehler mit ein.
Ein FH-Objektiv hat ein vergleichsweise großes Sekundäres Spektrum und einen geringen Gaußfehler.
Ein Poly-Strehl-Diagramm mit dem Optimum bei der Hauptfarbe Grün = e-Linie liegt, wird also dort das höchste
Strehlergebnis haben, während bei F und C der Strehl erheblich reduziert wird wegen der Defokussierung bzw.
Power. Der Gaußfehler fällt bei einem FH Objektiv kaum ins Gewicht. Ein Poly-Strehl-Diagramm wäre für diesen Fall
unsinnig, weil man bereits wegen der Defokussierung bei F und C sehr niedrige Strehlwerte hat ohne verwertbare
Aussage.
Damit grenzt sich die PolyStrehl-Darstellung auf die APO's ein mit einem vergleichsweise kleinen Sekundären
Spektrum. Eine Aussage kann deshalb nur für diesen kleinen Bereich Objektiv herangezogen werden, wie das untere
TSA-Diagramm zeigt. Die PolyStrehl-Darstellung verliert damit ihre Allgemeingültigkeit. Aussagekräftig würde die Sache erst,
wenn das Sekundäre Spektrum "kleiner" als der Gaußfehler in PV der Wellenfront wäre. Damit wären wir aber im Bereich
eines Super-APO's. Es läuft also auf den Versuch hinaus, eine ganz kleine Gruppe aller Objektive mit einem "Polystrehl-
Diagramm" vergleichen zu wollen. Und das wiederum ist nur die Spinnerei eines selbstverliebten Optik-Designers
und für die Praxis hingegen ohne Relevanz.
An der Frage, ob Fertigungsfehler der Vergleichbarkeit dienen oder sie verhindern, scheiden sich bereits die Geister.
Der unnütze Polystrehl-Begriff, Diverse Test-Reports,
Chronologie der Thematik
Am 12. März 2009 taucht der Begriff Polychromatischer Strehl über den Beitrag eines befreundeten
Designers erstmalig hier auf. Über folgende ZEMAX-Diagramme wurden über diesen Begriff die Unter-
schiede zwischen ED-APO's und Tripletts herausgearbeitet. http://rohr.aiax.de/@APOVergl01.jpg;
http://rohr.aiax.de/@APOVergl02.jpg; http://rohr.aiax.de/@APOVergl03.jpg
In der Folge wurde der gleiche Begriff von zwei bekannten Usern auf A.de und Astrotreff.de in einer
sehr verkürzten und unsystematischen Form regelrecht in Beschlag genommen. Ein Jahr früher, am
04. Juli 2008 veröffentlichte ich folgenden Bericht auf Astro-foren.de: Weißlicht-Bath-Interferometer für Massimo
In Beitrag #4 veröffentlichte ich mehrere Farb-Interferogramme in den Spektral-Farben, wie sie von
Optik-Designern beim Entwurf von Astro-Optik Verwendung findet.
Das fand frühestens am 01. Dez. 2009 seinen unsystematischen Niederschlag in einem Bericht hier:
http://www.astrotreff.de/topic.asp?TOPIC_ID=95328 Offenbar tut sich der dortige Beitrag schwer
mit den üblichen Spektral-Bereichen durch unübliche Wellenlängen. Die in diesem Zusammenhang
als "PolyStrehl-Diagramme" zu verkaufen beweist, daß das grundsätzliche Wissen fehlt. Auch eine
Quellenangabe fehlt, so daß man den Eindruck gewinnt, der dortige Verfasser holt sich regelmäßig seine
Anregungen auf unserem Forum und präsentiert dann dort das Ergebnis ungeniert als seine eigene
Entwicklung, auf die er im Bedarfsfalle noch geistiges Eigentum beansprucht. Noch nicht genug,
starteten zwei User aus diesem Dunstkreis auf unserem Forum den Versuch, uns mit wenig höflichen
Beiträgen ihre Sichtweise regelrecht aufzwingen zu wollen.
Ursprung aus Optical-Design-Programmen
Der Begriff polychromatischer Strehl, wie er als Tabelle(*) im Zusammenhang mit TMB und Takahashi-
Objektiven(**) veröffentlich worden war, ist das Ergebnis eines Optical Design Programmes, n i c h t
das Ergebnis einer realen Messung. Damit bleibt dieser Begriff im Bereich des Designs und ist nur
dort auf gleicher Ebene mit einem anderen Design vergleichbar und sinnvoll. Außerhalb dieses klar um-
rissenen Bereiches wird dieser Begriff mißbraucht, um verbissene, abgehobene Diskussionen zu führen
über den untauglichen Versuch, Farblängsfehler gemeinsam mit dem Gaußfehler in einer Indexzahl für
alle Refraktoren zu verknüpfen. Dabei ist man sich nicht der Schwächen bewußt, die dieser Begriff in
der Meßpraxis zeigt. Ein Optical Design Programm stellt also nur die theoretisch optimale Situ-
ation dar, aber keinesfalls Fertigungs-Fehler, wie systemübergreifende Überkorrektur, Flächenfehler,
Zentrier- Fehler, Astigmatismus etc. Diese Fertigungs-Fehler tauchen in diesem von Mathematik und
Design dominierten Bereich zumindest auf der Achse zunächst noch gar nicht auf.
Mir ist also kein allgemeiner Konsens bekannt, wie mit diesem Begriff exakt umzugehen sei.
Unvollständige Systematik:
Die auf den anderen Foren veröffentlichten Farb-IGrammen beweisen nur, daß Kurt nach drei Jahren
Anlaufzeit sein Equippement soweit vervollständigt hat und ein User Gerd das Zeichnen von Diagrammen
für informativ hält. Die Systematik des polychromatischen Strehls ist insofern unvollständig, als die
Betrachtung nicht nur auf die opt. Achse beschränkt bleiben dürfte, sondern auch auf die Situation im
Feld bezogen werden könnte, wie es Spotdiagramme ja tun. Im Bereich des Polychromatischen Strehls
käme man aber zu unsinnigen Ergebnissen, weil der Strehlwert über den Astigmatismus und/oder Coma
im Feld rapide sinkt und damit seine Aussagekraft verliert. Ähnlich verhält es sich bei Achromaten
auf der opt. Achse, wo der Farblängsfehler den Strehl über die Power gegen Null drückt, was einige der
Diagramme bereits sehr anschaulich beweisen. Ebenso fachfremd ist die Forderung, aus dem bisher üblichen
Strehl einer Meßwellenlänge, über alle Wellenlängen des sichtbaren Spektrums einen gewichteten Polychro-
matischen Strehl zu ermitteln, was bereits in der praktischen Durchführung mit vielen Hypothesen und Ein-
schränkungen versehen ist, und damit ohne jeden Nutzen für eine bessere Vergleichbarkeit von Refraktoren
untereinander. Die jahrzehntelangen bewährten Tests sind in jedem Fall viel effektiver und aussagekräftiger,
weil bereits ein ganz normales Zertifikat von den wenigsten verstanden wird. Siehe
hier.
Dem entgegen steht auch die in der optischen Industrie gängige Interferometer- bzw. Phasen Shift
Interferometer-Meßtechnik, die in der Regel bei 632.8 nm Wellenlänge eines Helium Neon Lasers
arbeitet. Oder in Form eines Fizeau- oder Twyman-Green Interferometeres bei 532 nm wave, dann
im grünen Spektrum. Mit einer solchen Ausrüstung ist ein polychromatischer Strehl eine Utopie,
weil interferometrisch überhaupt nicht darstellbar. Es fehlen nämlich die Interferogramme im
kurzen Spektrum, also z.B. bei 486.1 nm wave, was der F-Linie bei Fraunhofer entsprechen würde.
Daran ändert auch die Fleißarbeit eines Kurt nichts: Dieses Bild notfalls über die CopyFunktion
eingeben: http://www.astrotreff.de/upload/Kurt/20091201/Bi14.jpg hier. Seite 4
Die Anregung holte er sich hier: http://rohr.aiax.de/@Sepktral-Farben.jpg
http://www.astro-foren.de/showpost.php?p=37052&postcount=4 Wobei auffällt, daß er sich an
keinerlei Konvention hält.
Damit sollte man sich erst einmal begnügen, bevor man den Versuch startet, innerhalb der Meß-
technik selbst den Polychromatischen Strehl lauthals zu fordern. Selbst wenn er in irgendeiner
Weise zu realisieren wäre, ist die Vergleichbarkeit mit anderen Systemen das oberste Ziel,
und dann müssen, wie im Bereich des Designs, zu aller erst die Fertigungs-Fehler herausgerechnet
werden - sonst vermischt man nämlich Fertigung mit Design. Man würde einen TMB nur deswegen
schlechter darstellen, weil er wegen der Fassung astigmatisch reagiert. Ein Zeiss APQ, der zufällig
diesen Fehler nicht hat, würde dann besser abschneiden, eine Info zum Gaußfehler hätte man dann
aber nicht. Bei dem folgenden Zeiss APQ Nr. 011 hätte man z.B. zwei unterschiedliche PolyStrehl-
Werte, abhängig davon, ob mit oder ohne Astigmatismus, oder abhängig ob mit oder ohne Glasweg.
Der Astigmatismus war nämlich über einen Fehler mit dem Immersions-Gel entstanden, und wurde
deshalb behoben. Deshalb steht die Forderung, alle tatsächlichen Fehlerquellen in den Polychromatischen
Strehl aufzunehmen, der eigentlichen Absicht entgegen, Aussagen über den Gaußfehler zu machen.
APQ 105/800 Spannend wie ein Krimi - extrem farbrein
APQ 105/800 zweite Untersuchung nach Überarbeitung
Farblängsfehler-Vermessung
Nun war es wiederum meine Anregung vor ca. 3 Jahren, in definierten Spektren, also von der
h-Linie, g- und F-Linie, über e-Linie, d-Linie und C-Linie mit Hilfe von engen Interferenzfiltern mit einer
Bandbreite von ca.10 nm üblicherweise, Interferogramme fotografisch zu erstellen. Das aber nicht,
um der polychromatischen Strehl-Diskussion Vorschub zu leisten, sondern um die vermutlich
genaueste Möglichkeit darzustellen, wie man den Farblängsfehler auf der opt. Achse vermessen kann.
Das geschieht über die Streifen-Verkippung in den jeweiligen Spektren, wenn man die Streifen bei der
Hauptfarbe Grün auf Null stellt und die Abweichung bei Blau und Rot ausmißt, eventuell über den Power-
Betrag umrechnet, was aber ebenfalls mit Einschränkungen verbunden ist.
Ziel dieses Verfahren ist und bleibt die interferometrische Vermessung des Farblängsfehlers
eines Objektivs auf der opt. Achse, der eine RC_Indexzahl abliefert, über die alle Refraktor-Objektive in
ein überschaubares System einsortiert werden können. So machte es bereits Lichtenknecker vor
30 Jahren in seinen Tabellen, so machte es Zeiss ebenfalls, deren Optikrechner allerdings den Weg
über das optische Desing gingen, das mir bei einem Objektiv in der Regel unbekannt ist, weswegen
nur die Möglichkeit bleibt, den Farblängsfehler einer Optik real mit einer tausendstel Meßuhr in Form
von Reihenmessungen zu vermessen und diese dann zu mitteln. Über dieses Verfahren kommen bei
Refraktor-Optiken selbst aus der gleichen Serie oft differierende RC-Werte heraus, was mit dem
nicht immer gleichen Linsenabstand der Objektive zu tun hat. Die Anordnung der Farben bleibt aber
in er Regel erhalten, die ändert sich z.B. nur bei Verwendung eines Glasweges. Wenn, wie beim
Equinox passiert, der angegebene Objektiv-Durchmesser heimlich über okularseitige Blenden verkleinert
wird, dann nimmt ebenfalls die "Farbreinheit" zu, in der Hauptsache durch eben dieses Abblenden,
was zu einem sehr guten RC_Wert führte. Hier wurde ein deutlich überkorrigiertes 4.000.- Euro
teures FLT mit einem farbreinen Equinox verglichen, für den man ca. 1.500.- Euro zu bezahlen hatte.
In einem engeren Bereich zwischen manchen ED-APO's oder Triplets gewinnt der Gaußfehler
stärker an Bedeutung und es geht um die Frage, wie man im Vergleich zu einem anderen Objektiv
diesen Gaußfehler-Unterschied gewichten kann. Es geht also erneut nur um den Gaußfehler-Anteil
einer Optik in PV- oder Strehlwert, und nicht um weitere Fehler, die diese Optik vielleicht hat oder
auch nicht. Vergleichbar sind hinsichtlich des Gaußfehlers Optiken nur, wenn man - wie beim
Farblängsfehler auch - dieser Gaußfehler isoliert betrachtet wird, wobei der Gaußfehler durchaus
über einen Strehlwert oder PV-Wert dargestellt werden könnte, wenn man die Größe mit anderen
Systemen vergleicht. Und nur um der Vergleichbarkeit willen, muß man den Gaußfehler isoliert
betrachten, wie das auch bereits im Bereich des Desings so gehandhabt wird. Dort wird nämlich
nicht ein Polychromatischer Strehl angegeben, sondern lediglich in Tabellenform die spektralen
Einzelstrehls genannt, die man unter ZEMAX noch nicht einmal in einer Tabelle aufgelistet bekommt,
sondern einzeln ermitteln muß. Bereits die wenigen Veröffentlichungen legen nahe, daß über die
Einzelstrehls im Bereich Design hinaus aus gutem Grund kein Polystrehlwert in den Veröffentlichungen
selbst angegeben wird.
Wer im Jahre 2009 z.B. von LZOS ein hochwertiges Triplet kauft, bekommt üblicherweise ein
Zertifikat innerhalb der Hauptwellenlänge, in diesem Fall bei 532 nm wave. Also nicht etwa bei
Blau, Grün, Gelb und Rot und nicht etwa als Polystrehl über diese vier Farben dargestellt. Und
jeder halbwegs aufgeklärte Kunde weiß, daß Gaußfehler-bedingt im blauen Spektrum der Strehl
etwas niedriger ist, ebenso im roten Spektrum. Das über blaue oder rote Farbinterferogramme
nachzuweisen, würde allenfalls ein Kopfschütteln bei den Feinoptikern hervorrufen. Mit einer Meß-
wellenlänge von 532 nm ist dem gesamten Sachverhalt bereits ausreichend geschuldet, schon weil
der Strehlwert nur ein Kriterium in der Beurteilung von Refraktor-Optiken darstellt.
Und selbst wenn nun das Bath-Interferometer stärker zum Zug kommt mit seiner Fähigkeit, im
gesamten Spektrum Interferogramme zu erzeugen, dann käme erst einmal wieder die Forderung
der gemittelten Vielfachmessung im Einzelspektrum mit der ebenfalls nicht geklärten Gewichtung
der Teil-Ergebnisse zur Hauptfarbe Grün. Es entsteht also ein kompliziertes Gespinnst, das Zug
um Zug an Informations-Wert verliert, gefolgt von einer aggressiven Foren-Diskussion über
vernachlässigbare Größen und Details.
Im weiteren Verlauf entstehen dann mindestens zwei Strehl-Werte: Erstens der bisherige Strehl-
Wert, der innerhalb der Hauptfarbe oder dem tatsächlichen Optimum Aufkunft gibt über die
quantitative Qualität eines Objektivs und ein weiterer komplizierter PolyStrehl-Wert, der hauptsächlich den
Gaußfehler darstellen soll bei hochwertigen APO's. Bei einem Achromaten würde dieses Verfahren
den Strehl endgültig ins Bodenlose ziehen ohne jede Aussagekraft. Man hätte eine abgehobene
"Experten-Diskussion", die erfahrungsgemäß ganz andere Ziele verfolgt, als sachliche Information.
Ein Hersteller, Händler oder auch Kunde würde vollends den Überblick verlieren, bis auf diejenigen,
die glauben, mit dieser herstellungs- und praxis-fernen Idee zur "Aufklärung" beizutragen.
Vielleicht denken diejenigen den Sachverhalt in aller Gründlichkeit erst selbst einmal durch, bevor
sie mit unausgegorenen Forderungen die Szene überziehen.
Dabei geht es n u r um eine schlüssige Unterscheidung, was ist ein APO und was nicht.
Bereits die Vergleichbarkeit zwischen TMB und Takahashi ist nur eingeschränkt möglich!
Bei TMB fehlt die Gewichtung, Takahashi verwendet anderen Spektren.
Ungewichtete Tabelle spektraler Einzelstrehls: Quelle (*)
Der Orginal-Link funktioniert nicht mehr:
Quote:
Darstellung des Farblängsfehlers: Quelle (**)

Zur gleichen Thematik:
farbige Weißlicht-Interferogramme Zusammenfassende Übersicht
-----------------------
Passend zum oberen Thema entwickelt man dort: http://www.astrotreff.de/topic.asp?TOPIC_ID=95328 mit einer gewissen Hartnäckigkeit die
Polychromatische Strehl Diskussion weiter. Die daraus resultierenden PolyStrehl-Diagramme sind aus mehreren Gründen höchst angreifbar.
Interessant würden sie nämlich erst, wenn die untersuchten APO's ( und nur da wäre eine solche Untersuchung wirklich sinnvoll) hinsichtlich
der Qualität dicht beieinander liegen. Einen ED-APO (Zweilinser) mit einem Triplet APO zu vergleichen liefert nur wieder die bekannten Unter-
schiede ab, jedenfalls keine neuen Erkenntnisse.
Dieser User hat offenbar keinen Sinn für Konventionen. Die dort wahllos verwendeten Interferenzfilter entsprechen weder der TMB-Systematik,
noch der Takahashi-Tabelle, noch entspricht die Zusammenstellung den bei Optical-Design-Programmen üblichen Wellenlängen, also beginnend
mit violett = g-Linie = 435.8 nm wave (sieht man kaum noch), mit Blau = F-Linie = 486.1 nm wave, mit Blaugrün im Bereich 510 nm wave = die
Maximal-Empfindlichkeit unserer Augen in der Nacht, mit Grün = e-Linie = 546.1 nm wave, Gelb = d-Linie mit 587.6 nm wave oder D-Linie = 589.3 nm,
schließlich Rot = C-Linie mit 656.3 nm wave und wenn man so will die B-Linie mit 686.7 nm wave. Es gibt also keinen vernünftigen Grund, für das
blau-violette Spektrum gleich drei Farben zu benennen, obwohl dort der Gaußfehler stärker variiert. Für visuelles Beobachten steckt darin wenig
bis keine Information, außer man will zeigen, wieviel gesammelte Interferenzfilter man mittlerweile hat.
Mit gleicher Hartnäckigkeit überziehen uns auf astro-foren.de zwei andere User einsam und allein mit der gleichen Thematik, die für den
normalen Refraktor-Besitzer absolut keinen Informationsgewinn darstellt. Aber das ist wohl auch gar nicht der Sinn dieser Attacken, auf
die zu reagieren sich gar nicht lohnt.
Die jeweiligen Bilder kann man nur sehen, wenn man die Bildadresse oben in die Befehlszeile eingibt:
<<|http://www.astrotreff.de/upload/Kurt/20091212/X8.jpg|>>
436 nm liegt kurz vor der g-Linie = Hg-Emission
450 nm überflüssig weil zwischen g- und F-Linie, stammt aus der klinischen Chemie
475 nm liegt vor der F-Linie bei 486.1 nm also genau zwischen zwei Cd-Emissionslinien 470 nm und 480 nm
502 nm liegt vor 510 nm und zwischen 500 nm und 505 nm He-EmissionsLinien
<<|http://www.astrotreff.de/upload/Kurt/20091212/X9.jpg|>>
551,3 nm kurz nach der e-Linie stammt aus der klinischen Chemie mit 550 nm wave
588.3 nm soll vermutlich 598.3 nm heißen und wäre dann die D-Linie
656.2 nm soll vermutlich 656.3 nm heißen und wäre die C-Linie
675 nm wäre die Kr-EmissionsLinie mit 676 nm wave und schon wieder überflüssig
Damit wäre auch geklärt, aus welchem Bereich die Interferenz-Filter stammen. Ein Vergleich mit dem Pörschke-Katalog wäre da
durchaus sinnvoll gewesen. Wer einen PolyStrehl ermitteln will, sollte sich schon an die in diesem Bereich üblichen Konventionen
halten, wenn er ernst genommen werden will. Natürlich kosten derartige Filter auch noch Geld, was man eigentlich investieren
sollte.
Der ersten Übersicht kann man entnehmen, daß die Bereiche des visuellen Spektrums ziemlich gleich verteilt sind von g nach C.

Die Systematik findet man in jedem Feinoptiker Handbuch, das in keiner Bibliothek fehlen sollte.

Eine zusätzliche Übersicht liefert der Handel für feinoptische Bauteile

Passend dazu dieser Beitrag: http://www.astro-foren.de/showpost.php?p=44183&postcount=16
und dieser http://www.astro-foren.de/showpost.php?p=44190&postcount=18
Quote:
Zitat:
Hallo,
Man kann naterlich auf allen beliebigen Wellenlaengen testen, sogar im Infrarot oder Gammastrahlenbereich
wenn man will. Es ist nur dann schlecht mit anderen Publikationen vergleichbar die alle mit genau definierten
Wellenlaengen testen.
Solange man dann nur eigene Ergebnisse vergleicht ist das kein Problem.
Gruesse marty
E013A immer wieder Strehl
D045 C11 Star Bright XLT Nr. S29114 [http://www.astro-foren.de/showpost.php?p=61258&postcount=13]
Quote:
Was ich nicht verstehe ist so ein Testergebniss, den 1/8 wellenfront p.t.v ( ohne Koma, ohne Asti sogar 1/18 ) und über
96 % Strehl stellen ein optisches Systemmit extrem hoher Qualität dar. Dein defokusierter Sterntest und Rauheitstest sind jedoch
weit weit von solchen wahnsinnswerten weg. Dein In-Fokussterntest dagegen zeigt wirklich eine gute Optik mit gutem Kontrast
zwischen Beugungscheibchen und Beugungsring. Deine Interferogramme die du wohl zur Auswertung nimmst, mögen wohl solche
Werte ergeben Das sichtbare Streulicht im defokusierten Sterntest und im Lyot Test dagegen sprechen ein No Go für solch einen
hohen Strehl. Die stark sichtbaren Zonenfehler im defokusierten Sterntest sagen ebenfalls No Got für 1/8 wellenfront p.t.v.
Für mich passen deine Interferometrische Auswertung nicht mit dem defokusierten Sterntest und nicht mit dem Rauheitstest
zusammen. Gefühlsmäßig gebe ich dem System 80% Strehl und 1/4 wellenfront p.t.v. aber nicht mehr.
Den Anlaß für diesen Beitrag liefert der obere Link, weil in solchen Beiträgen - auch noch von einem Händler - ein völlig unzulässiger
Strehl-Begriff über die Foren transportiert wird. Obwohl das Internet an Informationen zum Begriff Strehl regelrecht überfließt, scheint
für einige "die Erde immer noch eine Scheibe zu sein!"
Auf einem Zeiss-Zertifikat in diesem Beitrag ist zur Definitions-Helligkeit (= Strehl, nächstes Bild unten) folgendes zu lesen:
Zit:"Definitionshelligkeit - Normierte Intensität im Bildpunkt
Die Definitionshelligkeit errechnet sich aus dem rms-Wert und erreicht bei einem idealen optischen System den Wert 100%"
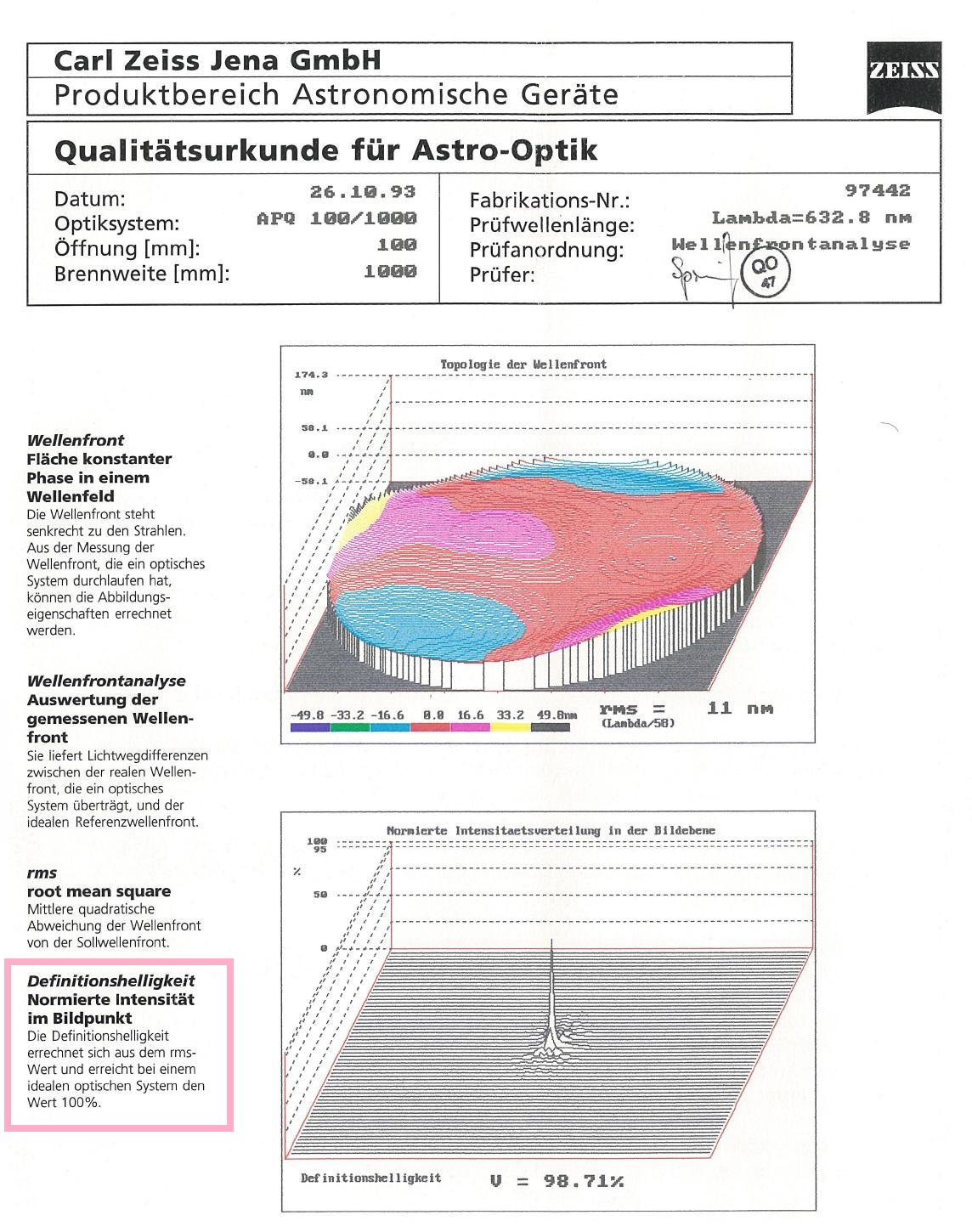
( Bei rms = 11 nm und 632.8 nm wave Wellenlänge ergibt das rms = Lambda/57.52 oder Lambda*0.017383059 oder 98.81% Definitionshelligkeit )
Die dazu nötige Formel lautet (über Taschenrechner ermittelt) Strehl = 2nd e^x (-(2*Pi*rms)^2) RMS-Wert in Strehlwert umrechnen
(Es ist also nur der rms-Wert in die Formel einzusetzen, keine Transmission, keine Reflektivität, keine Rauhheit etc, die alle nichts mit dem Strehlwert zu tun haben.
Auch ein unbelegter Spiegel hat seinen spezifischen Strehlwert.)
Optikprüfung mit Laserinterferometrie, Peter Rucks ...... In diesem Beitrag schreibt der Meßtechniker Dipl.-Phys. Peter Rucks, Zeiss, folgendes:
Quote:
Ein weiteres wichtiges Ergebnis der laserinterferometrischen Messung ist die Strehlsche Definitionshelligkeit (auch nur "Strehl" genannt), welche aus
dem rms-Wert errechnet wird. Sie ist definiert als das Verhältnis der Maximalintensität im zentralen Beugungsscheibchen der realen Abbildung eines punkt-
förmigen Objekts zu der Intensität, die in einer absolut fehlerfreien Optik bei gleicher Öffnung und Wellenlänge theoretisch dort erreichbar wäre. Da in der
Praxis kein optisches System absolut fehlerfrei ist, wird dieses Verhältnis immer kleiner als Eins sein (bzw. < 100% bei Prozentangabe). Die Definitions-
helligkeit ist nur von der Abbildungsqualität abhängig und nicht - wie fälschlich manchmal angenommen - von Reflexions- oder Trans-
missionseigenschaften einer Optik. [Anm: Dazu zählt auch die 'Rauhheit' von opt. Flächen, die lediglich Streulicht einführen, was sich jedoch kaum
quantifizieren läßt.]
Die TU Ilmenau liefert zur gleichen Thematik folgende Information: TU-Ilmenau_A , TU-Ilmenau B
Die folgende Übersicht mit Beispielen (Spherical, Koma, Astigmatismus) fußt auf dieser Information
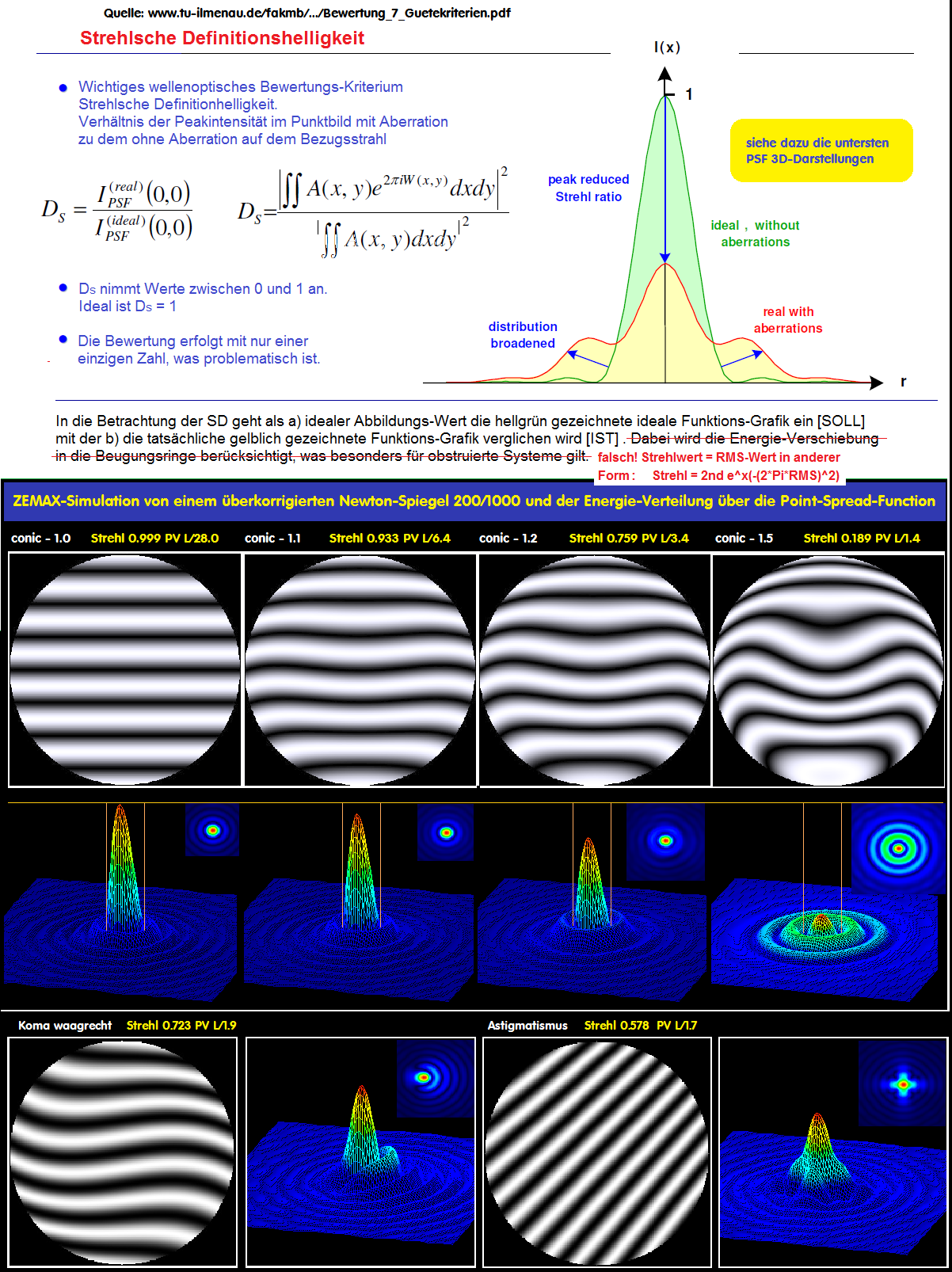
In keiner dieser Veröffentlichungen ist im Zusammenhang mit dem Strehlbegriff von Transmission, Reflexions-Eigenschaften, Rauhheit etc. ansatzweise die Rede. Bei der Rauhheit hat man besonders ein Definitions-Problem, in welchem Dimensions-Bereich man diese überhaupt ansiedeln möchte.
Das folgende Bild stellt ein gezeichnetes Interferogramm dar. Das linke Beispiel würde zu einem perfekten System gehören, also ohne Rauhheit etc. .
In das rechte Beispiel ist die Rauhheit einer "Schallplatte" eingearbeitet mit der Frage, ob sich bei einem solchen Interferogramm der Strehlwert ändert?
Es passiert also nichts! Wie weiter oben mehrmals ausgeführt, gehört die Rauhheit N I C H T zum Strehl-Begriff. [Die unteren Strehl-Schwankungen auf
der 3. Nachkomma-Stelle sind der Anzahl der benutzen Punkte zuzurechen. Bei vielen Punkten, wird die Berechnung etwas ungenauer.]
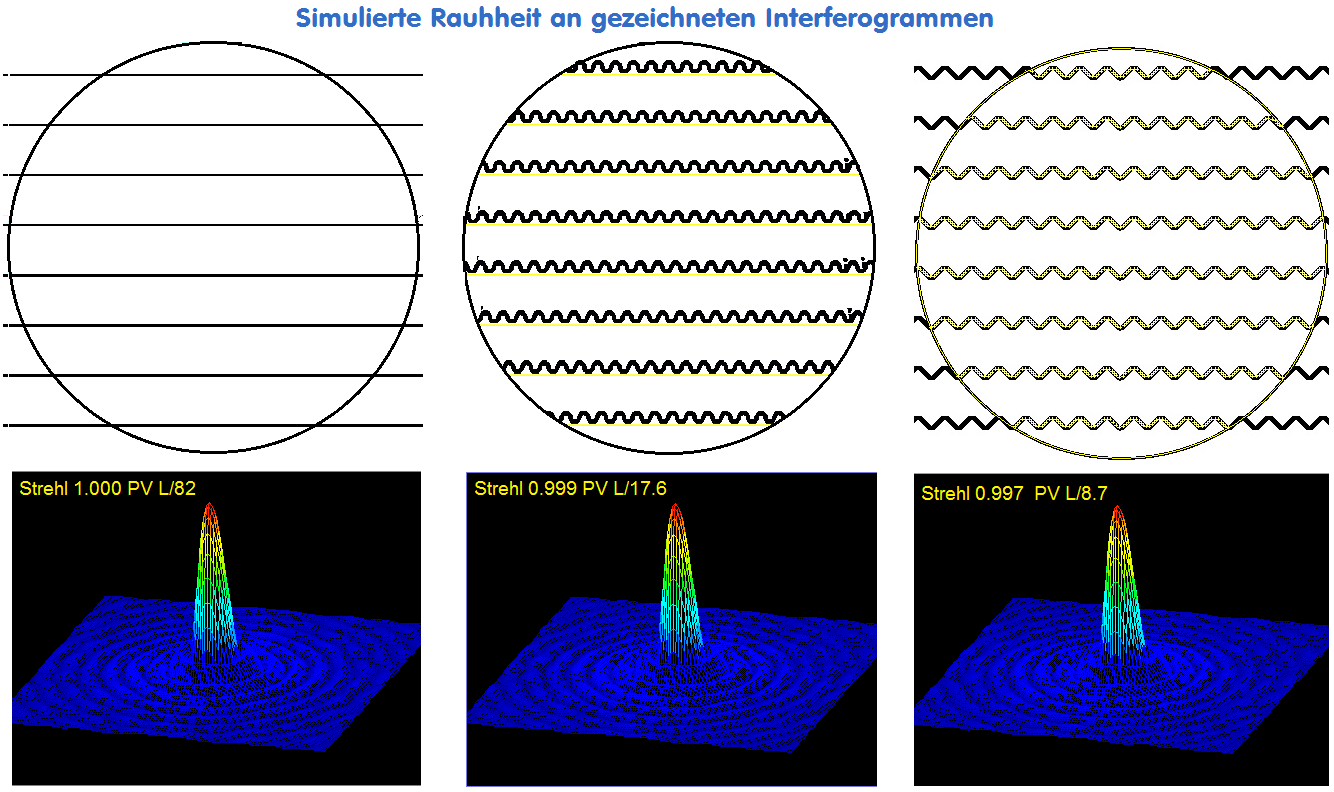
Auch im Bereich der obstruierten Systeme läßt sich der Vergleich zu unobstruierten Systeme über den Strehlwert nicht ziehen: Die Energie-Verschiebung bei obstruierten Systemen findet keinen Niederschlag im Strehlwert, was trotzdem manche nicht daran hindert, beide Systemvarianten über den Strehl- wert vergleichen zu wollen.
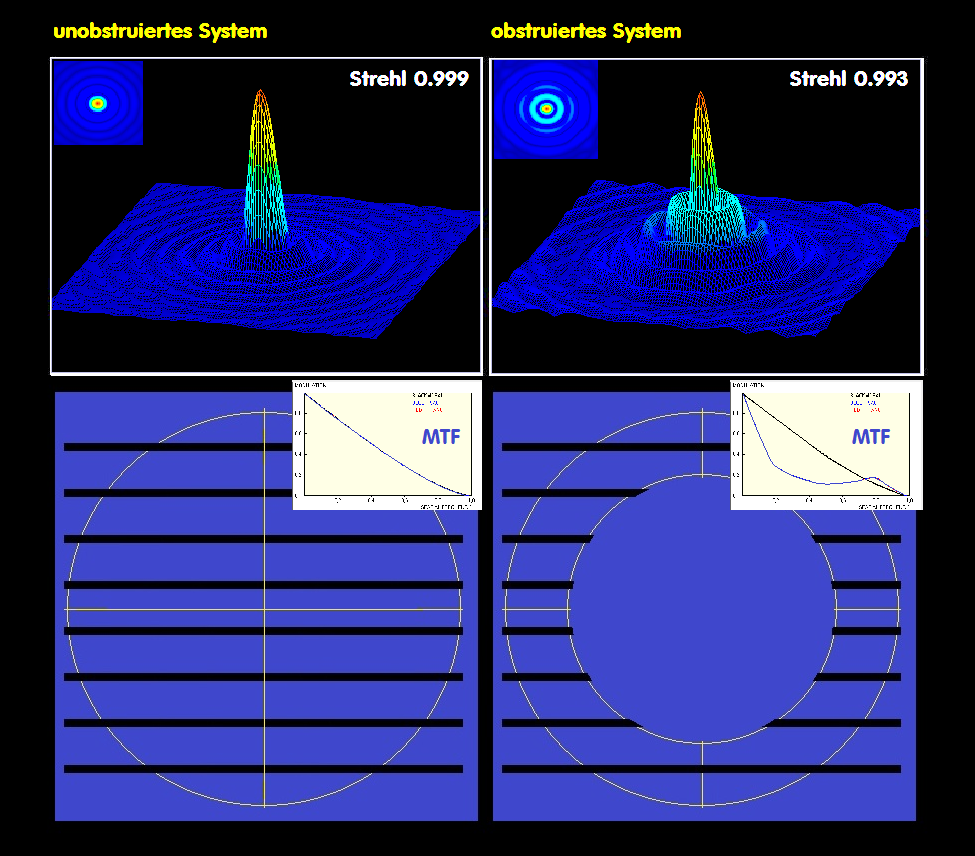
Wie sind denn nun die Begriffe Wellenfront, Strehl, Interferogramme aufzufassen ?
Der Begriff Wellenfront, wie er über die Zernike Koeffizienten systematisiert wird, beschreibt die Topografie, nicht die Feinstruktur einer Fläche. Bei
der Feinstruktur geht es um unterschiedliche Dimensionen, die man betrachten möchte: üblich sind 1 mm^2, die "Rauhheit" bezieht sich eigentlich auf 1 cm^2.
Der Begriff "Rauhheit" , wie er über den Lyot-Test dargestellt wird, ist also nicht exakt definiert. Unser Begriff von Rauhheit hat eher etwas mit den
Schlieren bzw. der Homogenität in der Schmidtplatte zu tun. In unserem Fall verursacht diese "Rauhheit" etwas mehr Streulicht, hellt also lediglich den Bildhinter-
grund etwas auf und hat, ebenso wie Transmission, Beschichtung etc. nichts mit dem Strehl-Begriff zu tun, der ein reiner "topografischer" (wellenoptischer) Ver-
gleichsbegriff ist zwischen dem SOLL und dem IST einer Optik.
Siehe auch: Scratch/Dig Reference Chart
Während beim Foucault-/Ronchi-Test die Topografie der Fläche dargestellt wird, erkennt man im Lyot-Test die Feinstruktur der Fläche im cm^2 Bereich
und liegt damit weit über den normierten Scratch/Dig-Einheiten. Der Begriff "Rauhheit" ist hier eine Mischung von Schlieren-Effekten und einer etwas un-
sanften Oberflächen-Retouche im cm^2 Bereich und ist deshalb aus verständlichen Gründen nicht normierbar.
Siehe dazu diesen Bericht: Spiegel-Rauhheit im Vergleich - Übersicht von Newton-Spiegeln
Zit:"Gefühlsmäßig gebe ich dem System 80%" gibt es in einer ernstzunehmenden Diskussion nicht.

Eine Diskussion zu diesem Sachverhalt mit dem eingangs zitierten User ist nicht "zielführend"[Zit. Merkel], da die Aussagen der ausgewiesenen Experten eindeutig sind. Deshalb schließe ich diesen Beitrag vorsichtshalber ab. Einen Strehl-Wert aus dem Sterntest ableiten zu wollen, ist Kaffeesatz-Leserei. Der Sterntest zeigt viel, aber nicht den Strehlwert !
-------------------------------------------
Obstruktion und sphärische Aberration (Spherical) Strehlwert und Obstruktion -
Auch bei der Obstruktion wird der Versuch gemacht, den Strehl-Begriff umzudeuten, indem man die Energie-Verschiebung in den 1. Beugungsring
vom Strehl-Wert abzuziehen versucht. Auch in diesem Fall ermittelt sich der Strehlwert aus dem RMS-Wert, und der entsteht ausschließlich über
die Topografie der Wellenfront. Der Beugungseffekt geht also in den Strehl nicht ein. Dazu bietet der Zeiss Meniscas ein interessantes Beispiel, weil
bei diesem aktuellen Teleskop eine leichte Überkorrektur im Spiel ist, die ebenfalls etwas mehr Licht in den Beugungsring verschiebt.

Bei obstruierten Systemen beobachtet man einen deutlicheren Beugungsring, gut auf dem Foto zu sehen. Die Auflösung, die man über das Foto
ermitteln kann, entspricht der Auflösung nach der Formel - zu finden bei Baader Tipps und Tricks . . .Strehlwert und Obstruktion -
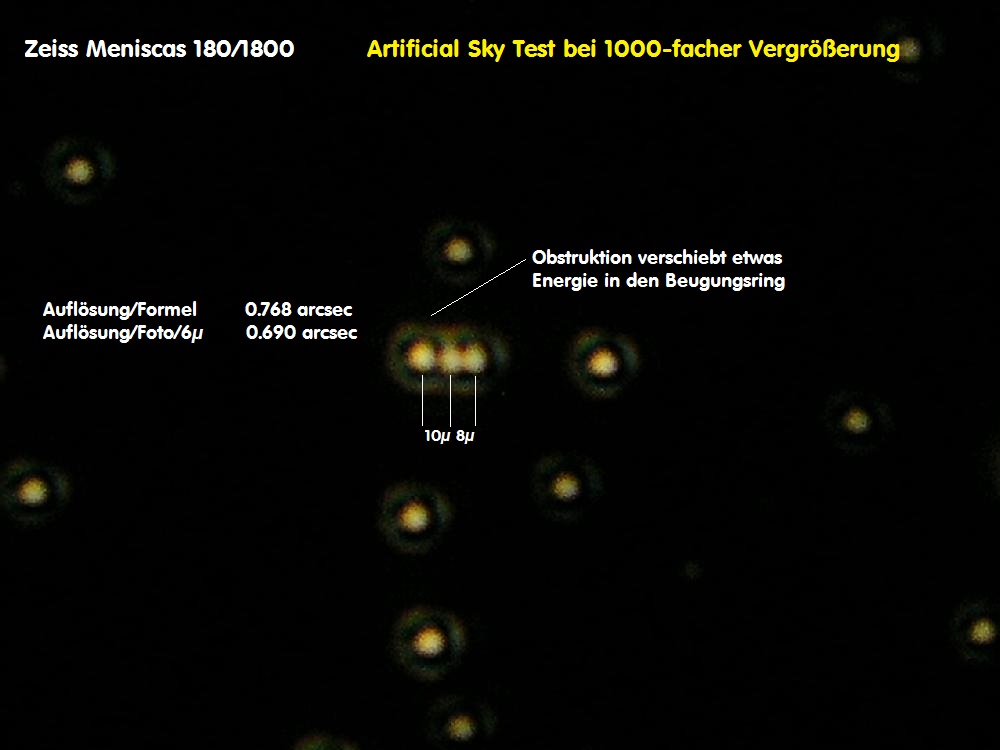
Diese Energie-Verlagerung ist in der Point-Spread-Function 3D-Darstellung gut zu sehen. Kommt noch Spherical hinzu, dann geht das Maximum in der
Mittel etwas zurück.
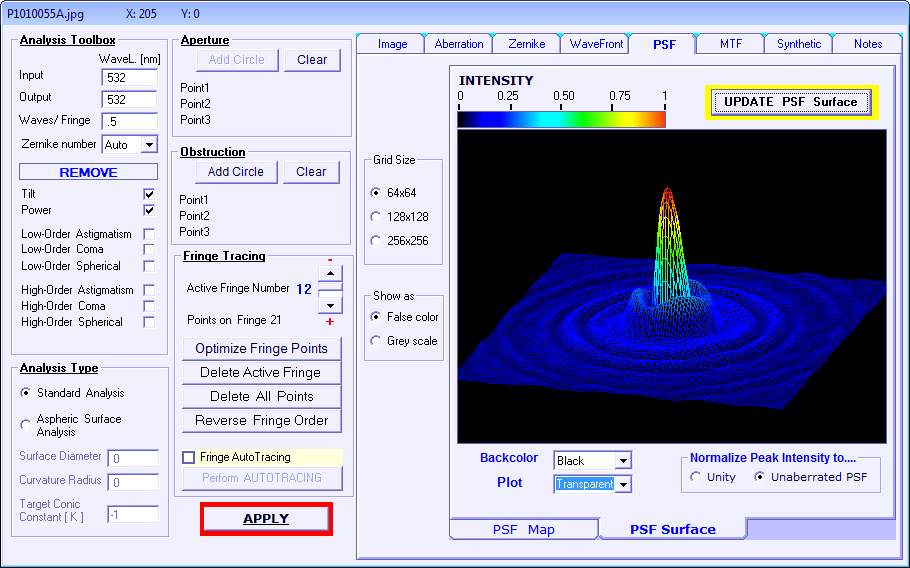
Die "M"-förmigen Bögen des Interferogrammes wären ein weiterer Hinweis auf die Überkorrektur.
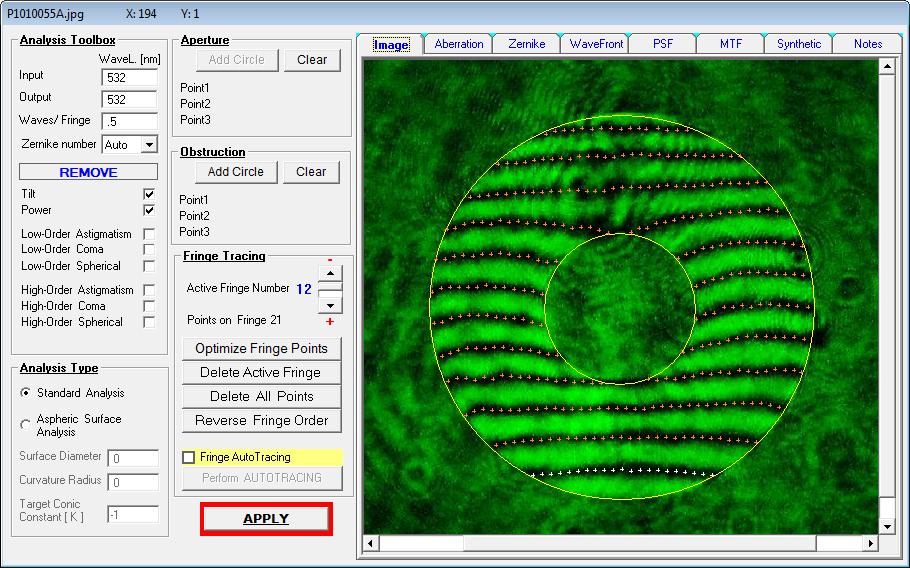
Die 3D-Darstellung der Wellenfront zeigt auf andere Art die Überkorrektur
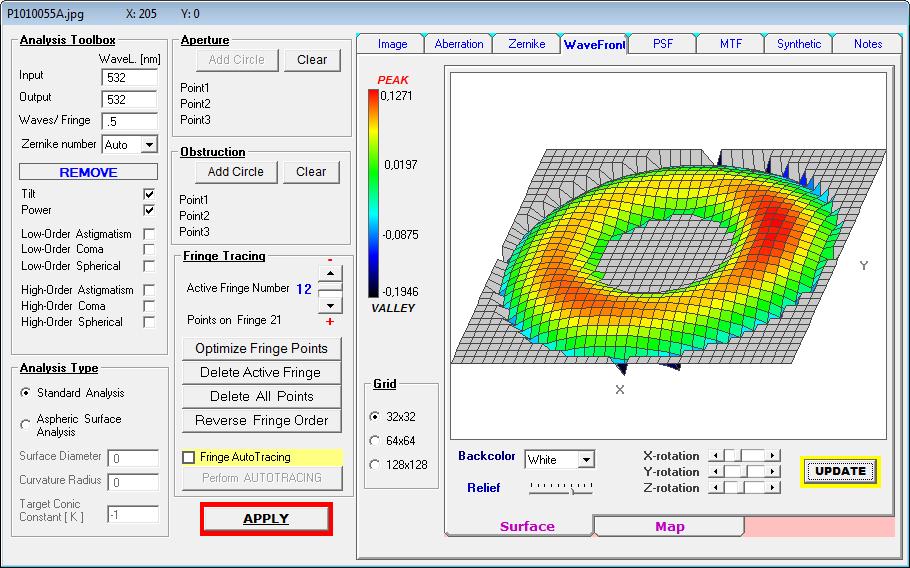
Das Focault-Bild entspricht dieser Darstellung
und abschließend die differenzierte Darstellung der Restfehler:
Die Überkorrektur ist mit PV L/4.4 beteiligt, ohne Überkorrektur wäre der PV-Wert bei Lambda/6.9 bzw. ein Strehl von 0.974.
Die anderen Restfehler sind verschwindend klein. Man wird diesem System also nicht gerecht werden, wenn man sich auf den
Gesamtstrehl von 0.844 fokussiert, und dieses System damit abwertet. An dieser Stelle ist der Strehlwert für eine
Beurteilung zu einseitig: Man wird die Glätte des Systems, die Farbreinheit und die perfekte Zentrierung unbedingt
berücksichtigen müssen und man wird feststellen, daß dieses System am Himmel erstklassige Leistung erbringt.
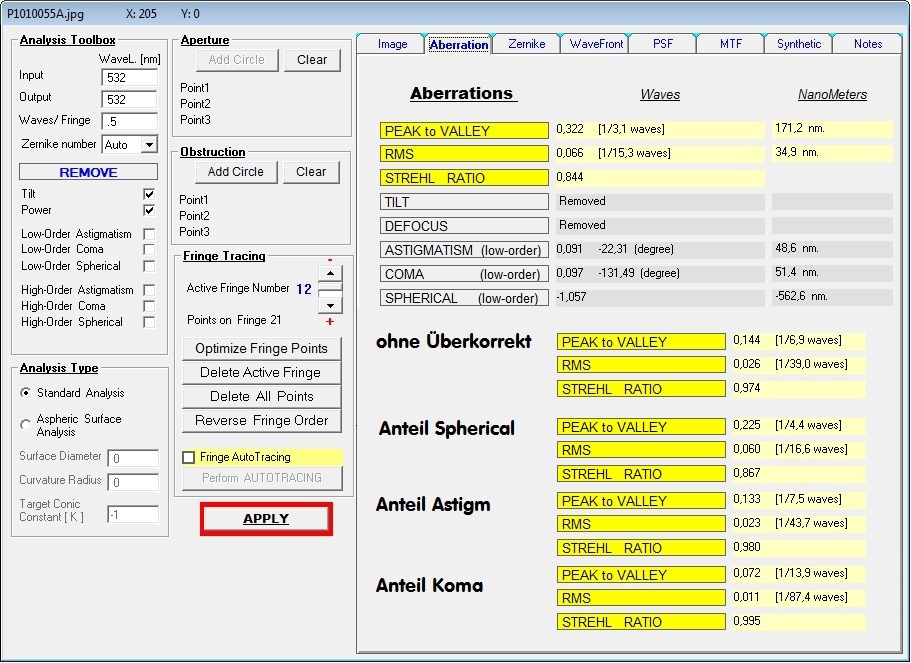
E029 -Test-Anordnungen astronomischer Optiken
- Test am Himmel in einfachem Durchgang
- Radius of Curvature RoC
- Setup in Autokollimation/Doppelpaß
- Kompensation über Dall-Null- und Roß-Null-Test
- Planspiegel gegen Sphäre prüfen
- Prüfverfahren astronomischer Optik - Übersicht
- http://rohr.aiax.de/vacuum.jpg LZOS VakuumTurm zu Testen
Test-Anordnungen - Einführung:
Zur Prüfung von Spiegel- und Linsen-Optiken gibt es ganz verschiedene Verfahren, je nach vorhandenen Möglichkeiten.
Der einfachste Test wäre der Sterntest am Himmel oder der Ronchi-Test, auch der Foucault-Test am Himmel liefert gute
qualitative Ergebnisse ab, die Astigmatismus, Koma und sphärische Aberration prüfen können. Ein quantitativer Test am
Himmel ist der Roddier-Test siehe hier. Alle diese Tests messen im einfachen Durchgang, also einfache Genauigkeit.
Im Labor kann man diese Situation mit einer Hilfs-Optik simulieren:

Ebenfalls am Stern zeigt dieses Bild eines Ronchi-Testes, mit den entsprechenden Ergebnissen. Damit wird in der Hauptsache
der Öffnungsfehler geprüft, also die Unter- oder Überkorrektur.
Bei jedem Test sollte man die Vor- und Nachteile kennen und den jeweiligen Test nicht verabsolutieren. Es empfiehlt sich immer
eine Gegenkontrolle über einen anderen Testaufbau, um das Test-/Strehl-Ergebnis zu bestätigen. Dies gilt besonders für den nächsten
Test in RoC = Radius of Curvature.
hilfreich.
RoC-Setup = Radius of Curvature
Für gewöhnlich wird eine Sphäre/Hohl-Kugel im Krümmungsmittelpunkt geprüft. Davon abweichende Spiegel, wie Ellipse, Parabel und
Hyperbel kann man ebenfalls aus dem Krümmungs-Mittelpunkt testen - wenn, ja wenn man die Fehlerquellen einer solchen Auswertung
genau kennt, sonst bekommt man falsche Ergebnisse.
Beim einfachsten Test einer Hohlkugel/Sphäre sitzt im Krümmungsmittelpunkt eine Lichtquelle. Die Licht-"Strahlen" werden von allen
Zonen dieser Sphäre als Bild in Totalreflexion wieder in den Ursprung zurückgespiegelt. Da eine Parabel im RoC in Achsnähe einen kür-
zeren Radius hat, nach erfolgter Parabolisierung, verformen sich die Streifen "M"-förmig in typischer Form zu einer Überkorrektur, was
die Parabel ja prinzipiell im Vergleich zur Kugel ist. Fokussiert man die Streifen in der 70.71 % Zone, dann entsteht das untere typische
Bild, bei dem Rand-Mitte-Rand auf einer Linie liegen. Siehe Vergleich im nächsten Bild.
Man prüft mit einfacher Genauigkeit, Streifenabstand 1 Lambda der Wellenfront, Scale = 1 !

Zurück zum Inhaltsverzeichnis
Beispiel einer RoC-Auswertung
Autokollimations-, Doppelpaß-Anordnung
Bei diesem Testaufbau prüft man vor einem hochwertigen Planspiegel mit doppelter Genauigkeit. Das Licht passiert die zu prüfende
Fläche zweimal: Vom Fokus der Optik zum Planspiegel, und von dort in Total-Reflektion wie4der zum Fokue zurück. Bei diesem Setup
kann man genaue Interferogramme erzeugen. Die Fehler-Quellen dieses Meßaufbaues sind gering, weil hier keine Umrechnung auf
Null, wie beim RoC-Setup stattfindet. Wobei jede Hilfs-Optik wiederum Fehler (z.B. Astigmatismus) einführt, den man entsprechend
zuordnen muß. Siehe hier:
Im folgenden einige Beispiele für Autokollimations-Setups.
Man prüft mit doppelter Genauigkeit, Streifenabstand L/2 der Wellenfront, Scale 0.5 bei Linsen-Systemen

bei einem Cassegrain, RC- oder SC-System: Die Schmidtplatte (bei Maksutovs die Meniskuslinse) würde rechts hinter dem Sekundärspiegel aber noch vor dem Kollimationsflat liegen.
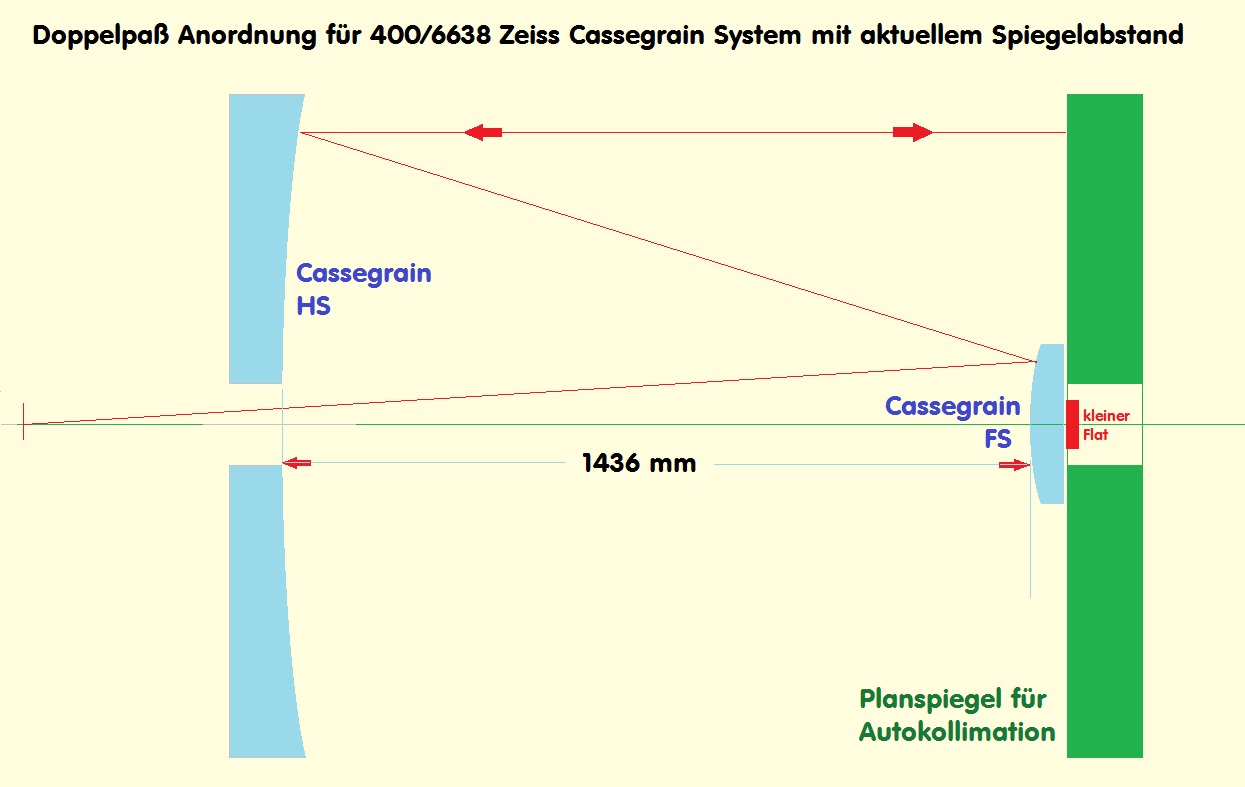
bei Newton-Spiegel

bei einem Cassegrain, SC- oder RC-System
Kompensations-Setupmit Plankonvex-Linse, Achromat oder Kugelspiegel
Mit diesem Testaufbau kompensiert eine Plankonvex-Einzel-Linse (Ross-Null-Test) die sphärische Aberration der Parabel,
aber auch Ellipse oder Hyperbel. Der jeweilige Abstand der Einzel-Linse zum Prüfspiegel muß jedoch über ZEAMX oder ein
anderes Optical Design Programm ermittelt werden. Ein Beispiel dafür ist dieses Bild:
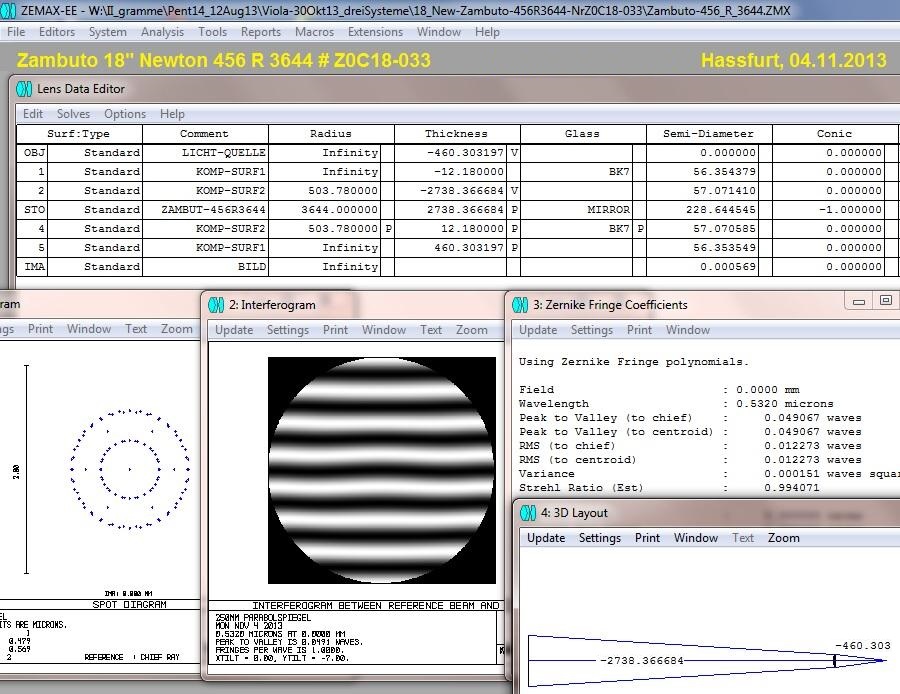
Bei diesem Setup prüft man mit einfacher Genauigkeit, Streifenabstand 1 Lambda der Wellenfront, Scale = 1! Auch bei diesem
Setup kann man alle Tests durchführen, muß aber die Farbzerlegung der Einzel-Linse mit einem grünen Interferenz-Filter
eingrenzen. Dieser Test funktioniert nur, wenn man den Abstand Linse zu Spiegel richtig gerechnet hat. Auch den Sekundär-
Spiegel von Cassegrain/RC-Systemen kann man so durch die hintere Glasfläche vermessen.



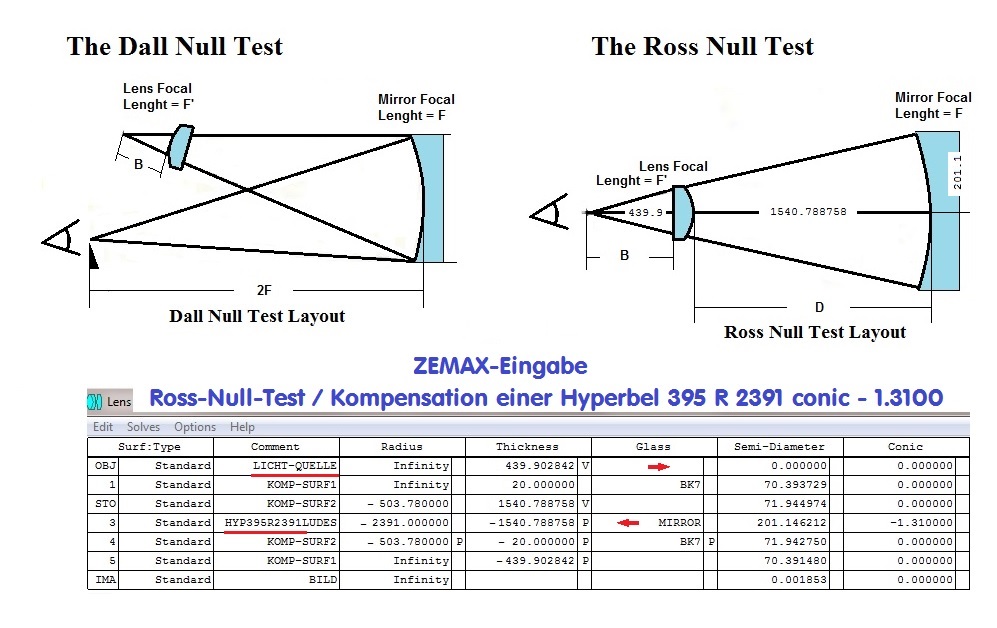
Prüfung von Plan-Flächen
Planflächen kann man ebenfalls auf sehr unterschiedlich Weise prüfen: Entweder in Kontakt gegen eine Referenz-Planfläche,
kann auch eine Wasseroberfläche sein, oder gegen einen hochgenauen Kugelspiegel, wie von Ronchi veröffentlicht.
Man prüft mit doppelter Genauigkeit, Streifenabstand L/2 der Wellenfront, Scale 0.5
Man prüft mit einfacher Genauigkeit, Streifenabstand 1 Lambda der Wellenfront, Scale = 1!

Der Rayleight Water Test - Messen gegen eine Wasseroberfläche
E072 - Flat 10 inch prüfen - 12.04.2014
Ein Kollimations-Planspiegel sollte unbedingt zwei Kriterien erfüllen: a) Die Regelmäßigkeit sollte unter PV L/10 liegen und besser. Er sollte also weder Zonen, Rillen und dergleichen haben und er sollte b) eine möglichst glatte Oberfläche haben, damit Rauhheits-Messungen mit dem Lyot-Test möglich sind. (In einem Autokollimations-Setup wird der Flat 1x benutzt, der geprüfte Parabol-Spiegel hingegen 2x. Die Planität bzw. Power hat hingegen nur untergeordnete Bedeutung, ein Radius von 6 km spielen keine Rolle, weil es sich um eine Total-Reflexion handelt.
Einen Planspiegel könnte man gegen eine Wasser-Oberfläche prüfen, oder gegen eine Referenz-Fläche. In der Regel hat man diese Einrichtung nicht. Der italienische Physiker Vasco Ronchi hat Planspiegel z.B. gegen eine Sphäre geprüft, was aber voraussetzt, daß man eineentsprechend genaue Sphäre hat.
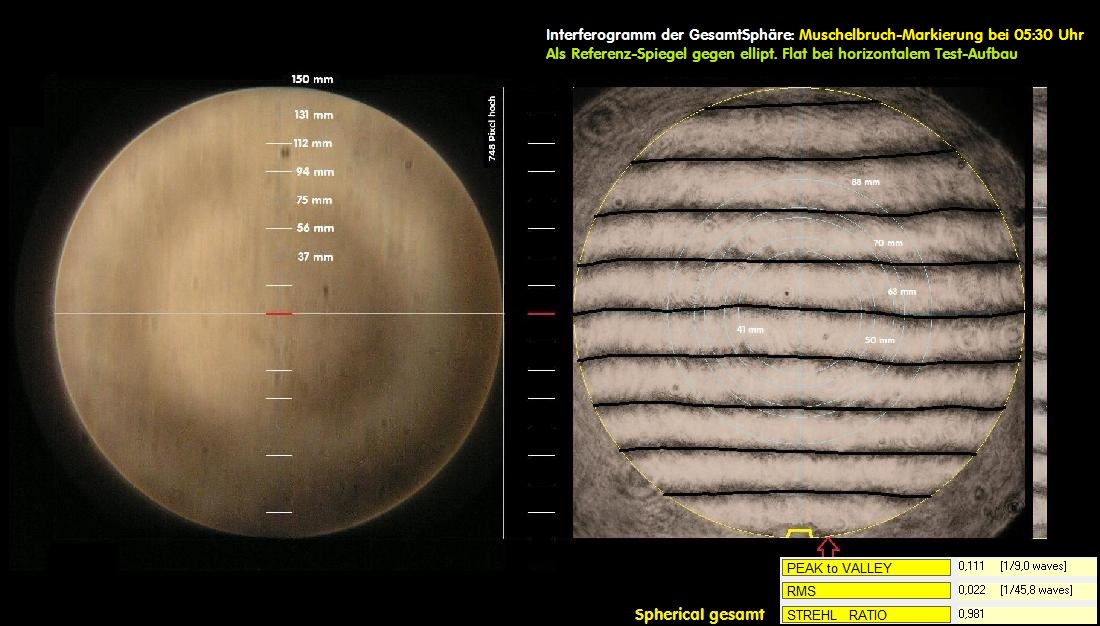
http://www.astro-foren.de/showthread.php?14243-elliptical- Flats&p=62856#post62856
Das folgende Bild zeigt den Testaufbau gegen eine möglichst genaue Sphäre.

.
Dieser Test steht und fällt mit einer möglichst genauen Sphäre, bzw. man sollte immer die Test-Ergebnisse der Sphäre mit dem Flat-Sphäre-Setup vergleichen. Auch sollte die Fläche der Sphere möglichst glatt sein. Vor Jahren diente mir ein Spiegelschleifer seine 16" Sphäre an, die aber leider eine ziemlich rauhe Oberfläche hatte. In diesem Fall war der Spiegelschleifer äußerst gekränkt - weil manche Spiegelschleifer ein herausragendes Selbst- bewußtsein haben.

.
Auf den Durchmesser hat die Sphäre eine "weiche" Zone in der Gegend von ca. PV L/8. Der Vergleich beider Bilder zeigt, daß sich diese Zone in beiden Setups abbildet. Da die Zone dem Kugelspiegel zugeordnet werden muß, ist der Planspiegel in jedem Fall besser, also ohne dies Zone.
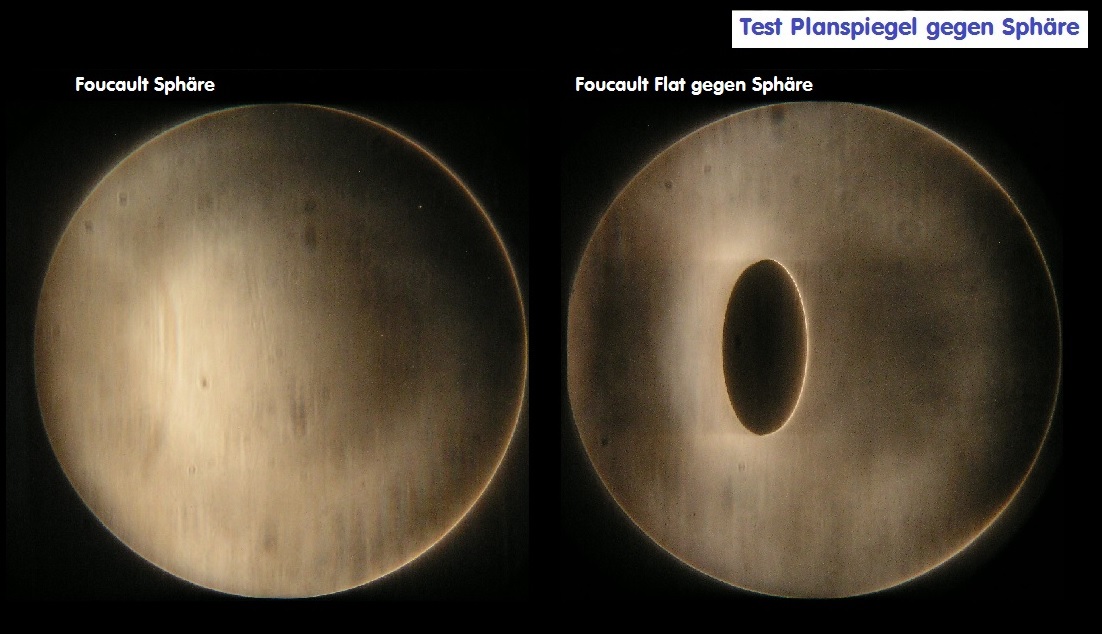
.
Auch im Ronchi-Test mit 13 lp/mm intrafokal bildet sich der gleiche Sachverhalt ab, betrachtet man die Fläche zwischen 0% bis 50%. Hier ist die Zone nicht so deutlich zu sehen, aber im Vergleich ebenfalls wahrnehmbar. Zwischen den dünnen Beugungslinien und den hellen breiteren Streifen zeigt die "dunkle" Linie, daß die Planspiegelfläche sehr glatt sein muß: Bei rauhen Flächen sieht man in diesen dunklen Linien die Störungen in der Politur, die Micromamelonnage.

.
Die Rauhheit im cm^2 Bereich ist schwer zu deuten. Sie gehört in jedem Fall auch zur Sphäre. Irritierend ist dabei der vertikale Strukturverlauf, bei dem sich ein vorhandener Astigmatismus mischt, der mehrere Ursachen haben kann.
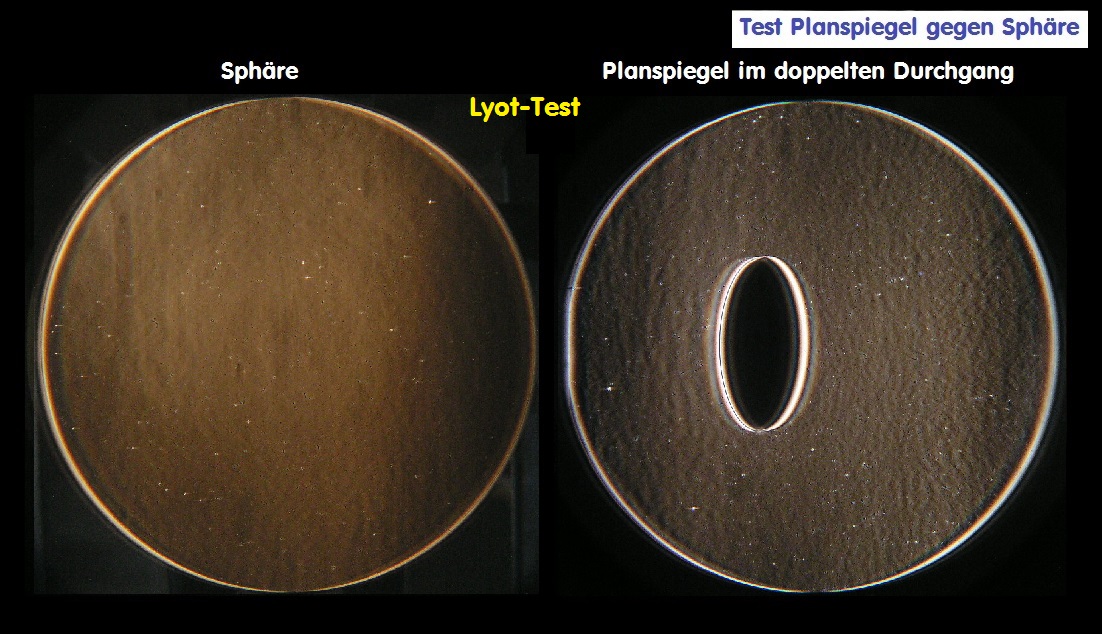
.
Beide Interferogramme bilden den Restfehler der Sphäre ab. Links mit einfacher Genauigkeit wäre die flache Zone ebenso zu erkenen, wie im Gesamt-Setup mit dem Planspiegel zusammen. Die Wellenfront-Abweichung in beiden Setup's haben ebenfalls gleiches Aussehen, sodaß erneut der Fehler des Kugelspiegels abgebildet wird. Lediglich der PV-Wert weicht in beiden Systemen etwas voneinander ab. Was der Unschärfe bei solchen Auswertungen geschuldet ist.

.
Zwei Aufnahmen aus dem Prüfprotokoll: Die Power mit ca. 6 km kann man als unbedeutend vernachlässigen. Sehr viel bedeutender ist ein möglicher Rest-Astigmatismus, der hier aber ausgeschlossen werden muß. Wenn man aber diesen Planspiegel aber in einem Winkel von 45° prüft, dann sorgt die Power von ca. 6 km für einen Astigmatismus im Test-Ergebnis. Den muß man dann aber abzuiehen. Da Parabol-Spiegel am besten in einem Zwei-Stufenverfahren geprüft werden, prüft man den ParabolSpiegel zunächst in a) RoC-Setup auf Rest-Astigmatismus in gleicher Weise, wie das auch dieser Spiegelschleifer gemacht hat, und erst dann prüft man b) gegen einen Kollimations-Flat auf sphärische Aberration, bei dem man Koma sowieso und Astigmatismus deaktiviert. Den Astigmatismus kann man bereits vorher isoliert auswerten.

.
Eine ganze Reihe weiterer Test folgten:
- zunächst ein Autokollimations-Vergleich an einem 300/1500 Newton-Spiegel, (als Gegenkontrolle den 12" in Kompensation, damit man dessen Auffälligkeiten sieht.) da geht es besonders um den abfallenden Rand des 250 Flat, der nur vermeidbar wäre, wenn man nach Fertigstellung den Rand abschleifen würde. 240 mm ist garantiert und geprüft.
- ein Autokollimations-Vergleich mit einem 150/1500 Lichtenknecker Newton-Spiegel, der vor 40 Jahren mit hoher Präzision geschliffen wurde.
..hier kann man den Bereich im Zentrum um die Bohrung prüfen. Als Gegenkontrolle kann man diesen kleinen Newton-Spiegel in RoC prüfen, ob die Streifen homogen verlaufen, also keine Zonen zeigen.
Auf diese Weise lernt man diesen Kollimations-Flat intensiv kennen, bevor er als Referenz-Fläche verwendet wird.
..
.