Aktuelle Seite: Startseite > Berichte > 03 Newton-Systeme und verwandte Fragen > Berichte > 05 Messtechnik - Teil 1 > E084 * Hyperbel - Konische Konstante und Zonenfehler
E084 * Hyperbel - Konische Konstante und Zonenfehler
E084 *
A - Hyperbel - Konische Konstante und Zonenfehler;
B - elliptical Flat
C - andere Setups , Hindle-Sphere, Waineo-Test, Foucault-Schnittweiten-Messung, Hindle-Sphere, Waineo-Test, Foucault-Schnittweiten-Messung
AMATEUR TELESCOPE MAKING, Book one, S225, "A new test for Cassegrainian ... secondary mirrors" Mounthly Notices of the Royal Society , March 1931;
Hyperbel
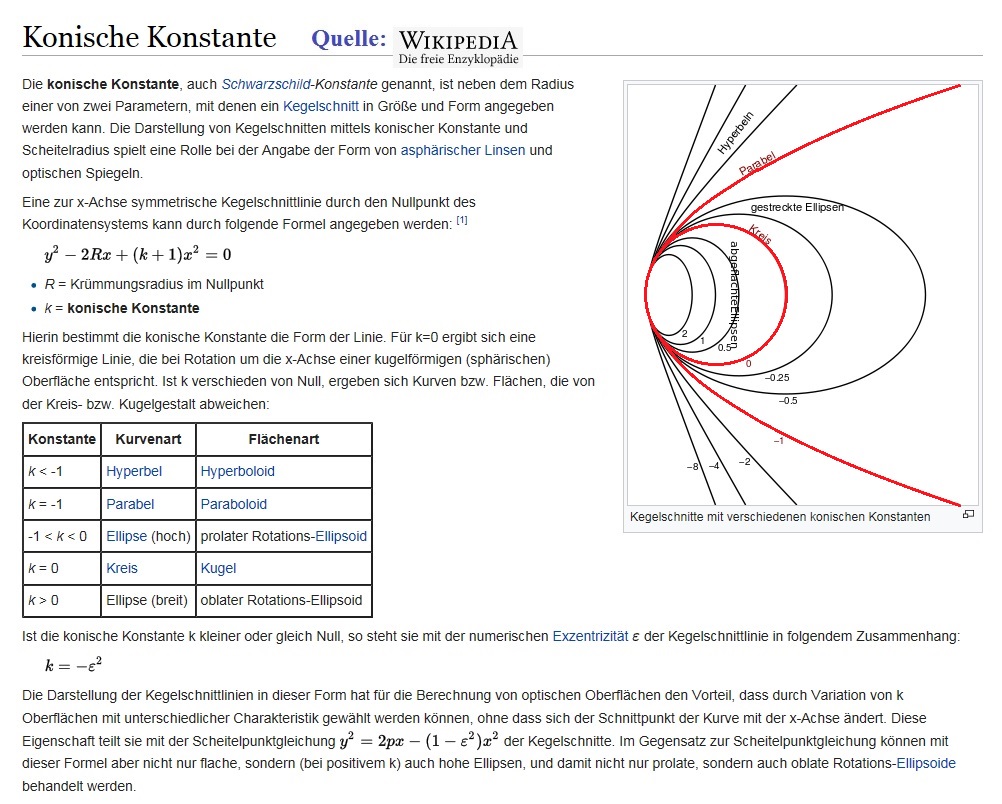
Besonders bei Newton-Spiegeln taucht sie auf: Die konische Konstante mit -1 für eine Parabel. bei RC-Systemen hat man es mit zwei
Hyperbeln zu tun: für den HS eine etwas schwächere { -2.0 < Hyperbel < -1.0 }, für den Sekundärspiegel etwas stärker { -5.0 < K < -3.0 }.
Bei langebrennweitigen Spiegel-Systemen kommen Rotations-Ellipsoide vor (Dall-Kirkham/Mewlon), ebenso ist die Asphäre bei man-
chen Optiken ebenso eine Kegelschnitt-Rotations-Fläche. Im vorliegenden Fall sieht sich der Hersteller dieses Hyperbolspiegels außer-
stande, die erzielte Konische Konstante heraus zu geben, sodaß man über diverse Setups den Versuch startet, die Konstante zu ermitteln.
-
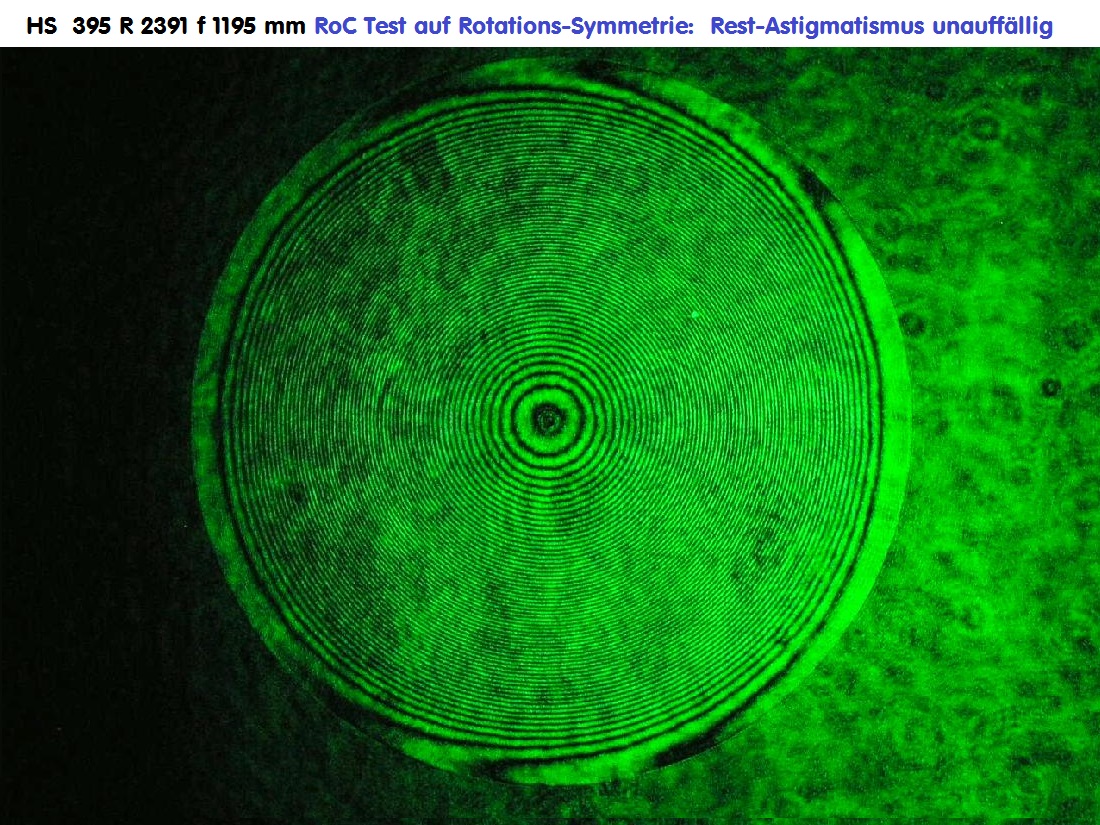
Wegen diverser Berechnungen braucht man die Spiegeldaten im Krümmungsmittelpunkt: Durchmesser 395 mm Radius im Scheitel 2391 mm.

-
Der erste Test überprüft die Rotations-Symmetrie, bzw. einen möglichen Rest-Astigmatismus. Dieser Befund ist unauffällig, aber auch
deswegen schwierig, weil wegen der Hyperbel sehr viele Streifen im Spiel sind.
-
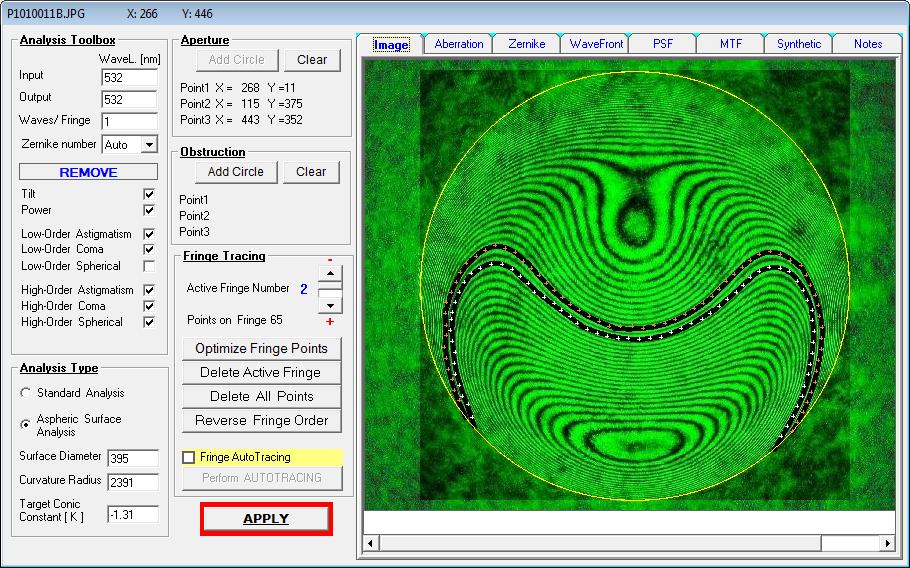
Da man über AtmosFringe in RoC eine Parabel auf Null zurückrechnen kann, geht das natürlich auch bei einer Hyperbel. Betrachtet man
für diesen Fall nur die Sphärische Aberration, dann genügen bereits zwei Streifen, um ungefähr auf die Konische Konstante zurückzurechnen.
-
Im ersten Durchgang wären das dann K -1.310, wie im folgenden Bild zu sehen
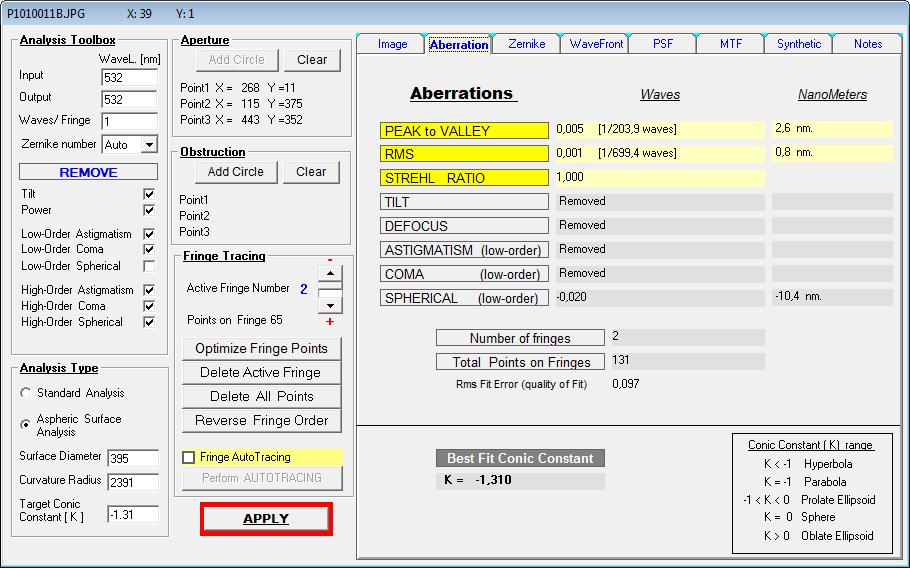
-
Steckt man diese K = 1.310 in eine ZEMAX-Kompensations-Berechnung so ergibt sich ein HS / KompLinsen-Abstand von ca. 1541 mm.
Wäre dieser Spiegel perfekt, also ohne jede Zone und exakt der Wert K = -1.310, dann würde das Interferogramm etwa wie das untere
synthetische IGramm aussehen.
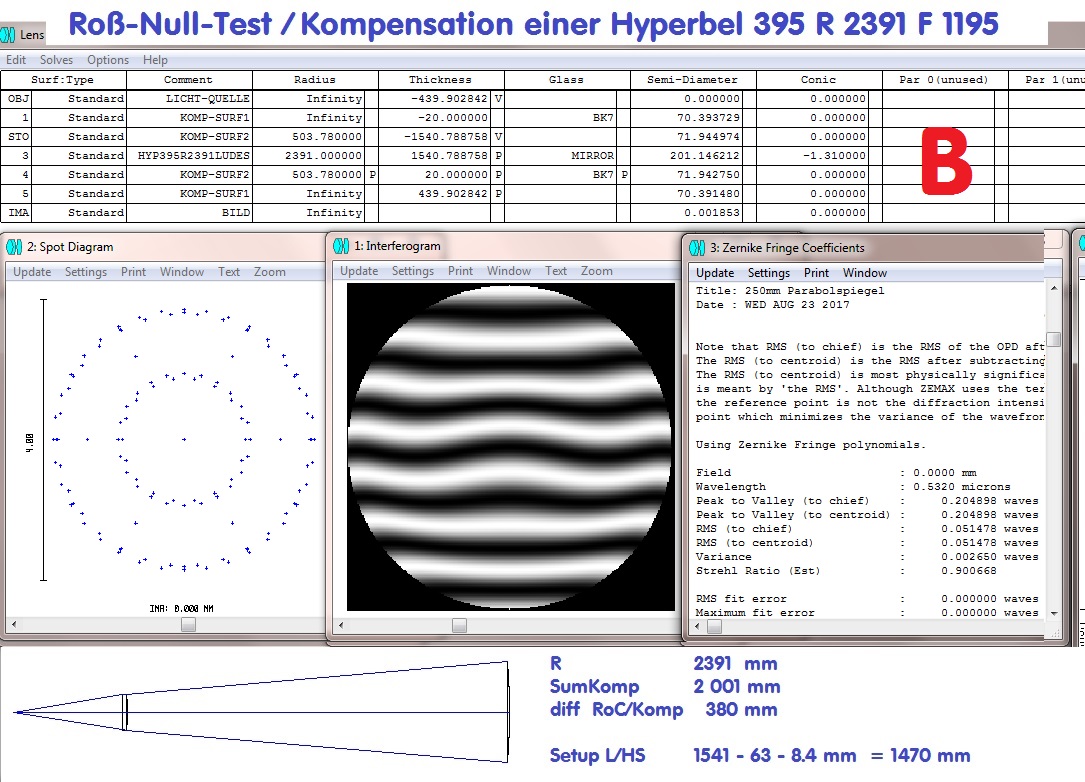
-
Passend zur oberen Berechnung also der Testaufbau mit dem errechneten Abstand 1541 mm
Der Hubtisch auf dem die Komp-Linse steht, wird seitlich durch eine Holzplatte geführt, sodaß man auf einfache Art den
Abstand Linse - Hauptspiegel variieren kann.

-
Das auffälligste Merkmal in diesem Fall wäre die Zone bei ca. 90% vom Durchmesser, eine Art Ringwall.
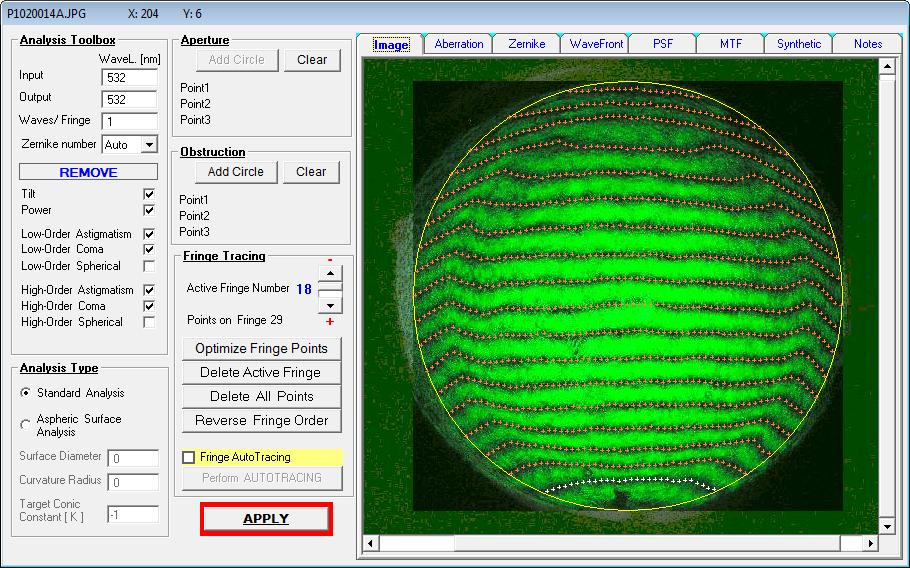
-
Das Ergebnis kann man sich ebenfalls mit AtmosFringe zeichnen lassen, und jetzt faßt das Programm diesen Fehler als unterkompensiert
auf. Der HS-Linsen-Abstand muß also verkürzt werden, damit die Kompensations-Wirkung zunimmt.
10 mm Abstandsverkürzung, also 1531 mm führt aber bereits zu einer über-kompensierten Wirkung, sodaß das Optimum in der Gegend
von 1536 mm liegen müßte.
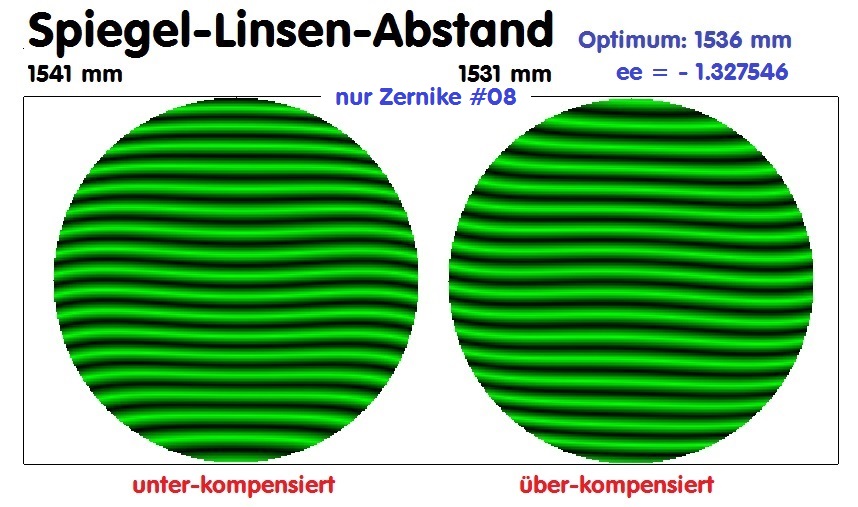
-
Schließlich setzt man diesen Abstands-Wert wieder in ZEMAX ein, und bekommt den Wert K = -1.327546
Mich würde nun interssieren, a) welchen Wert der Designer in seiner Berechnung hatte, und b) welchen Wert der Optik-Hersteller
für den HS überzeugend ausweisen kann. Wie diese Konische Konstante in das vom Designer entwickelte System paßt und wie
sich das Ergebnis in der praktischen Prüfung verhält, muß jedenfalls noch untersucht werden.
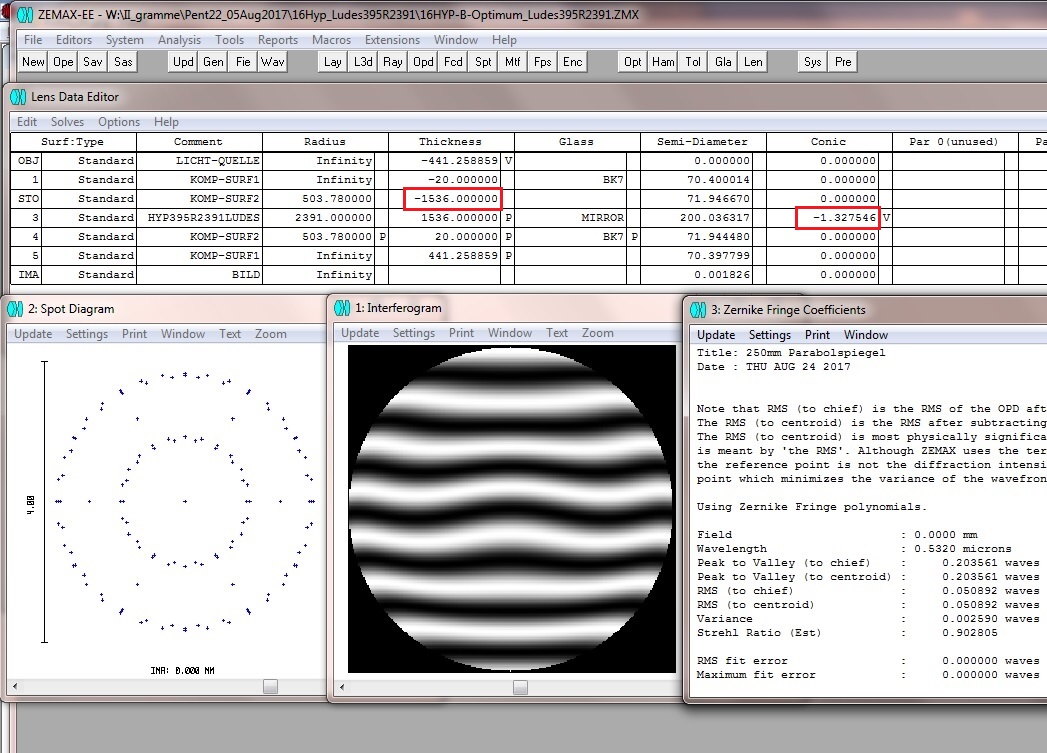
Der optimale Abstand Spiegel - Linse von 1536 mm
Der Zernike Zoo: http://r2.astro-foren.com/index.php/de/2-uncategorised/61-der-zernike-zoo-5-april-2006
Unter dem optimalen Abstand von 1536 mm Spiegel / Linse sieht man deutlich die Zone bei ca. 90% vom Durchmesser, ebenso beim Ronchi-Test
intrafokal, 13 lp/mm. 
Die Auswertung von Spherical Low + high ergibt einen Strehl von 0.572, wie er in der Hauptsache über die Zone verursacht wird,
mit PV L/1.5 High Order Spherical. Da Low Order Spherical nur die Über-/Unterkorrektur darstellt, in ähnlicher Weise wie die Power,
wäre damit der richtige Abstand zwischen Linse und Spiegel mit 1536 mm erreicht. 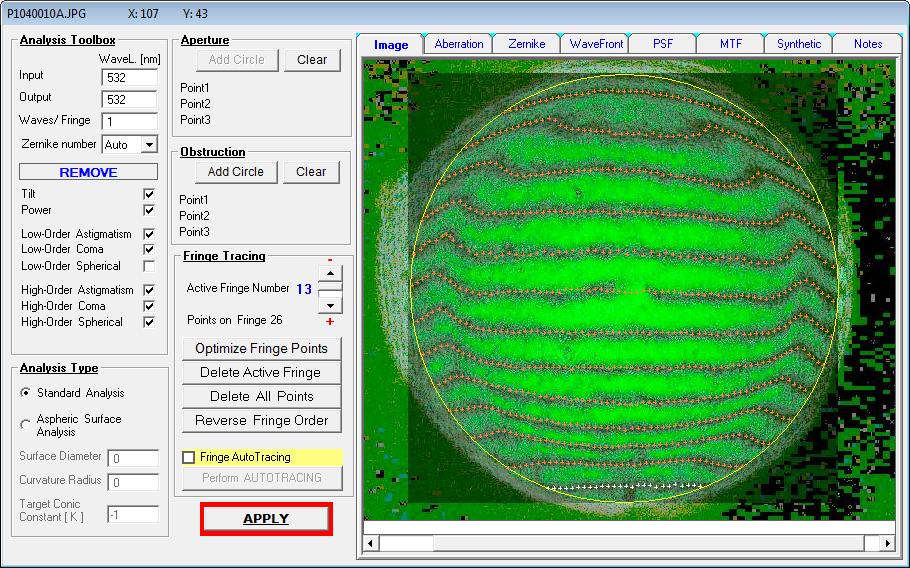
Und nur für Low Order Spherical gilt der Strehlwert von 0.994 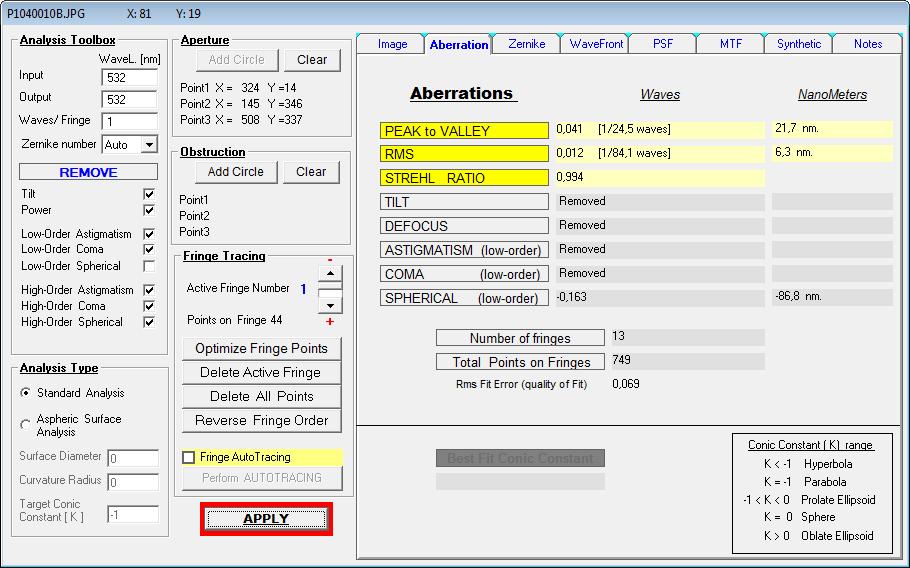
Der Unterschied zwischen Low Order Spherical im Synthetischen IGramm (links) und der Summe von Low + High Order Spherical sieht man
dagegen rechts mit dem synthetischen IGramm und einem Strehl von 0.572 . Ob allerdings diese Genauigkeit des Hauptspiegels für ein
optisches System Hyperbel + Korrektor genau genug ist, muß noch untersucht werden. 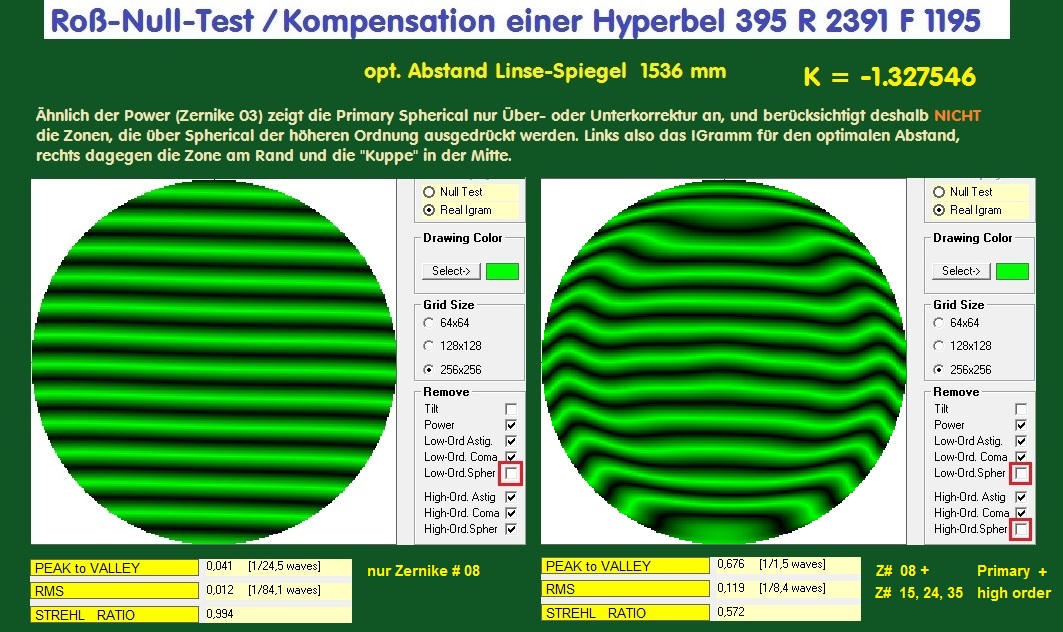
Elliptical Flat
Elliptical Flat - Frage der erforderlichen Genauigkeit
Bei der Beurteilung des elliptical Flats kann man mindestens zwei Standpunkte vertreten: Die erste Genauigkeits-Angabe bezieht sich
auf die Gesamt-Spiegelfläche. Für diesen Fall wäre der Gesamt-Strehl bei 0.758, ein vergleichsweise guter Wert über die Gesamtfläche,
wenn man nicht gerade die Gesamtfläche im Strahlengang verwenden möchte. Dann hat man eine Situation, wie bei den beiden Astro-
Kameras, die ich Anfang der 80-er Jahre gebaut habe.
C018 * Bath-Astrokamera AKI(Freiburg) und AKII(Namibia)
C019 * Bath-Astrokamera AKI und AKII Systemdaten und Bilder

Für diesen Fall braucht man nicht die Spiegel-Gesamtfläche im Strahlengang, sondern nur die Teilfläche, die der Lichtkegel jeweils im
Strahlengang tatsächlich braucht. Statt des Gesamtdurchmessers Ellipse/kleine Achse = 190 mm, wäre nur ein Kreis mit ca. 65 mm
Durchmesser (ja nach Position des Flats) zu berücksichtigen, und die Genauigkeit steigt entsprechend - letztlich eine Frage, mit welcher
Genauigkeit man die Fläche bestellt hat. 
Für die Gesamt-Fläche 190 mm wäre dann der Strehlwert 0.758 - im anderen Fall rechtes Bild mit 65 mm Durchmesser Strehl 0.980.
Da diese Newton+Korrektor-Kamera für visuelle Zwecke gebraucht wird, kann man einen solchen Wert tolerieren. 
AndereSetups
Andere Setups: Hindle-Sphere, Waineo-Test, Foucault Schnittweiten-Differenz-Messung
Die verschiedenen Setups in der Literatur:
https://www.google.de/search?q=Hindle+Sphere&tbm=isch&tbo=u&source=univ&sa=X&ved=0ahUKEwjnyazGrI7WAhUC7xQKHU21CusQsAQIMQ&biw=1622&bih=1031
http://www.telescope-optics.net/hindle_sphere_test.htm
http://www.telescope-optics.net/waineo_null_test.htm
http://www.telescope-optics.net/dall_ross_null_test.htm
In allen Fällen ist es sinnvoll, über einen anderen Test zu prüfen, ob bei einem anderen Testaufbau ähnliche bis gleiche Ergebnisse
entstehen. Man kann den HS auch über den Waineo-Test prüfen, also gegen einen Kugelspiegel. Da gibt es offenbar zwei Lösungen,
wobei die zweite Lösung sehr ungenau ist. Auch empfiehlt sich ein einfacher Foucault- oder IMeter-Test, bei dem die Schnittweiten-
Differenz zwischen Mitte ujnd Rand des HS gemessen wird.
Das folgende Setup benutzt eine Sphäre im doppelten Durchgang und kompensiert in ähnlicher Weise die Aberration der Hyperbel.
Allerdings wäre die Lichtquelle zwischen den Spiegeln, was die Messung etwas schwieriger macht. Der Vorteil ist die Herstellung der
korrigierenden Sphäre, die sich leichter prüfen läßt, als eine große Plankonvex-Linse. Sie ist dem Roß-Null-Test insofern ähnlich,
als auch hier die Sphäre im doppelten Durchgang benutzt wird. Siehe auch: http://www.telescope-optics.net/waineo_null_test.htm 
In einem anderen Setup muß der sphärische Kompensations-Spiegel eine Bohrung haben. Hier wird die Sphäre im einfachen Durchgang
verwendet, der hyperbolische Test-Spiegel jedoch im doppelten Durchgang. Der Nachteil dieser Anordnung scheint zu sein, daß die exakte
Bestimmung der Konischen Konstante bei diesem Setup "unschärfer" ist, weil der Spiegelabstand eine großere Toleranz hat und damit
die Ermittlung ungenauer wird. 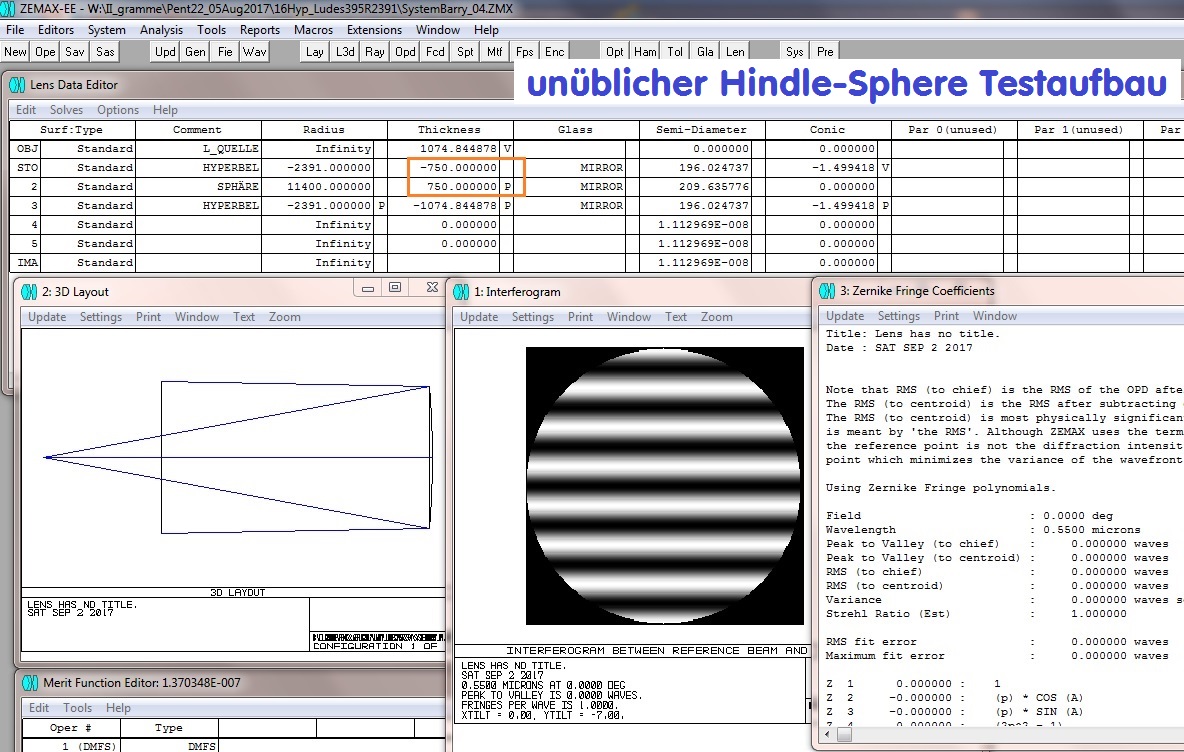
Eine Art Gegenkontrolle wäre eine Zonen-Differenz-Messung, wie man sie vom Foucault-Test kennt. Dabei reicht die Differenz zwischen
Mitte und Rand, bzw. zwischen der 0.707 und der Mitte.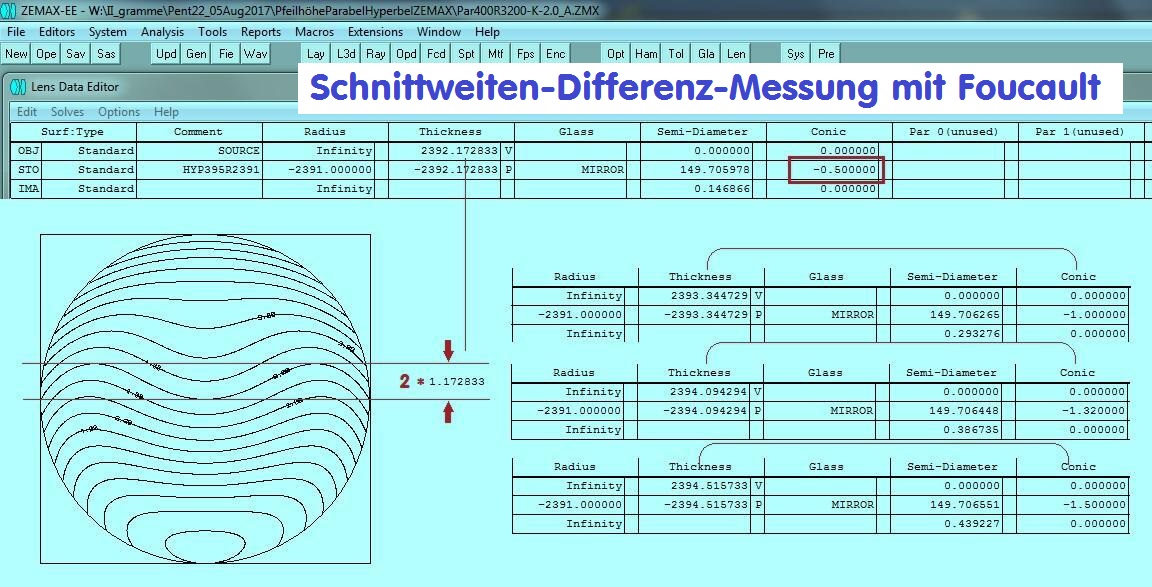
Über ZEMAX läßt sich die Schnittweiten-Differenz (Mitte-0.707-Zone-Rand) rechnen zwischen Mitte und Rand. Weil es hier die Differenz
zwischen Mitte und der 0.707-Zone ist, muß der Wert noch mit dem Faktor 2 multipliziert werden. Damit ist überprüfbar, ob die Hyperbel
tatsächlich den gerechneten Wert bzw. die erfoderliche Größe erreicht hat. Bei KoKo -1.32 wäre das dann 6. 188588 mm im Unterschied
zu KoKo -1.50 und 7.031466 mm. Dieser Unterschied wäre dann als weiteres Test-Kriterium genau genug, um die richtige Hyperbel dar-
zustellen. Statt dem Foucault-Test kann man auch einen InterferoMeter benutzen, wobei die Streifen der jeweiligen Zone waagrecht und
parallel sein muß. Mit einer 0.001 mm Meßuhr und einer Reihen-Messung wäre das hinreichend genau.
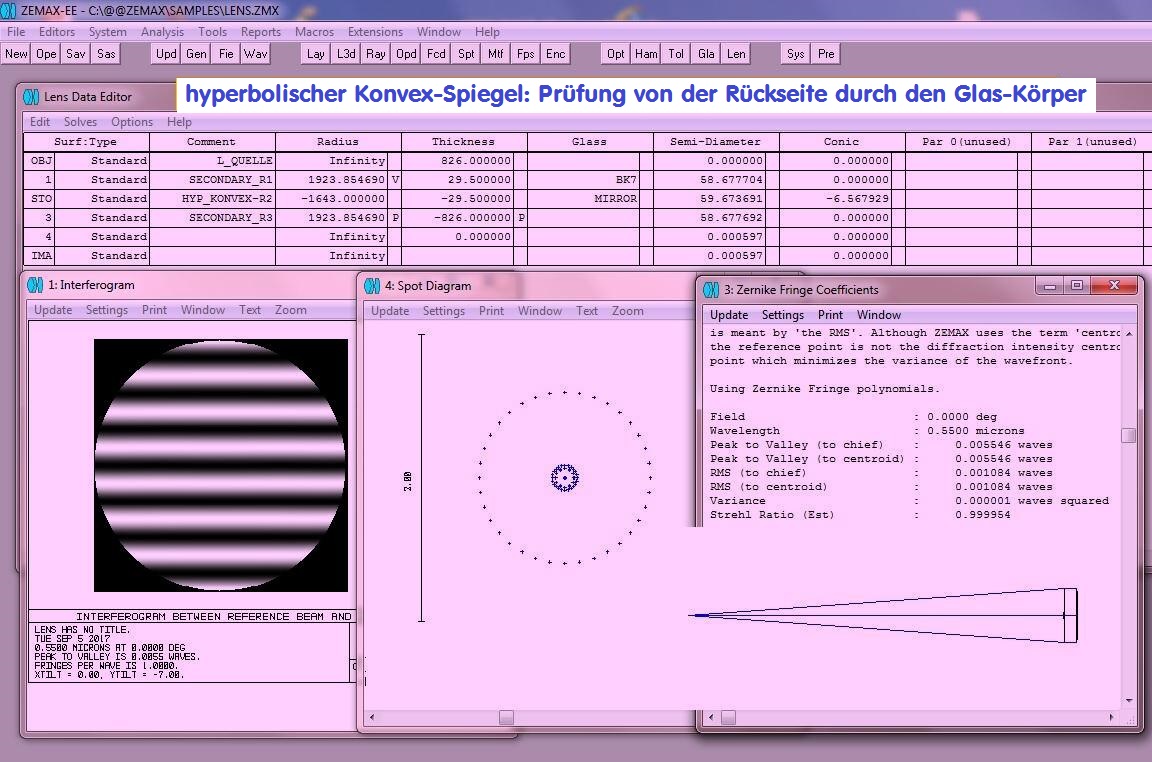
Secondary Konvex-Spiegel: Test der Hyperbel von der Rückseite durch den Glaskörper BK7 oder ähnlicher Gläser.
Für diesen Fall wird der Glaskörper als Linse verwendet. Dadurch entsteht eine Kompensations-Wirkung und man kann die Hyperbel
sehr genau auf Null prüfen.