Aktuelle Seite: Startseite > Berichte > 11 Vermischtes + Jahrgänge > Berichte > 05 Messtechnik - Teil 1 > E085 * Ross-Null-Test / Kompensation einer Hyperbel
E085 * Ross-Null-Test / Kompensation einer Hyperbel
Vorbemerkung bzw. der Anlaß (überarbeitet am 16.09.17, am 22.09.17)
August 2017 erreichte mich ein hyperbolischer Hohlspiegels mit Durchmesser 396 mm und 2391 mm Radius im Ursprung. Der Hersteller
jedoch weigerte sich, einen genauen Nachweis zu führen, welche konische Konstante dieser Hauptspiegel denn nun hätte. Im Design wird
eine konische Konstante von - 1.5 verlangt, die von der Firma offenbar nicht erreicht worden war - jedenfalls entstanden im System keine
entsprechenden Punktabbildungen besonders im Bildfeld. Ich wurde deshalb gebeten, die konische Konstante am konkreten Spiegel zu
ermitteln:
http://r2.astro-foren.com/index.php/de/berichte/05-messtechnik-teil-1/2-uncategorised/773-e084-hyperbel-konische-konstante-und-zonenfehler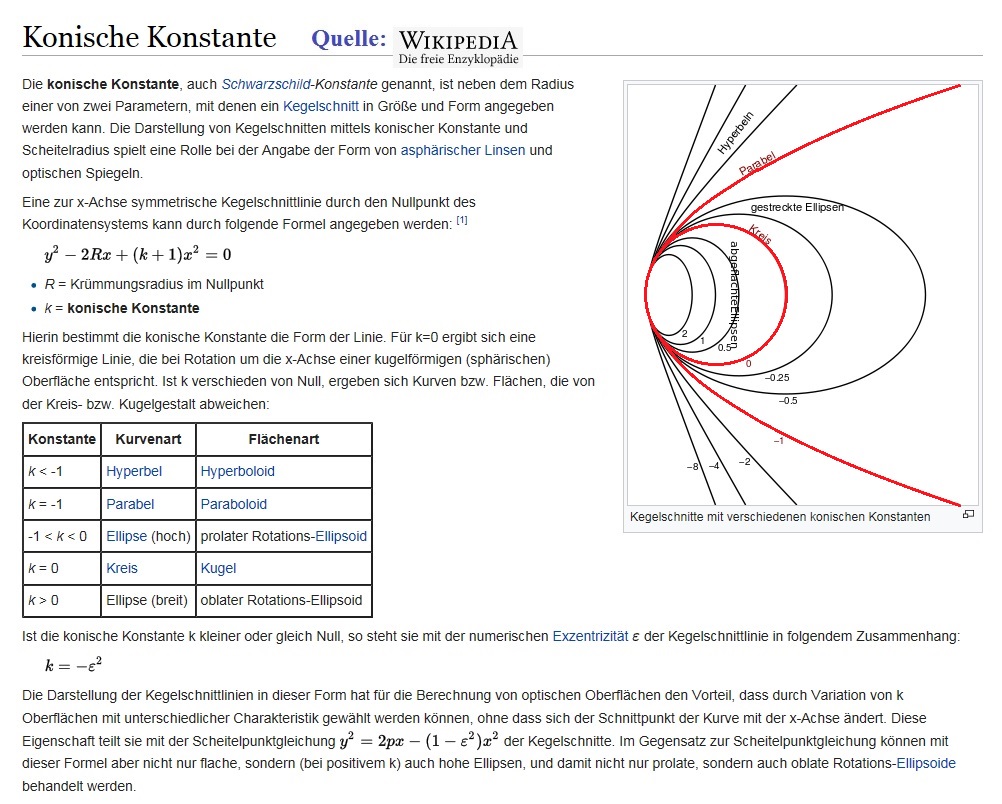
Die Lösung über den Ross-Null-Test:
Beim Ross-Null-Test folgt auf die Lichtquelle links eine Plankonvex-Linse und danach der Hyperbolspiegel. In einem errechneten Abstand,
siehe das folgende Datenblatt in ZEMAX, kompensiert die sphärische Aberration der Linse die sphärische Aberration des Hyperbol-Spiegels
auf Null. Das Programm optimiert auf die richtigen Abstände und die richtige Conic constant.
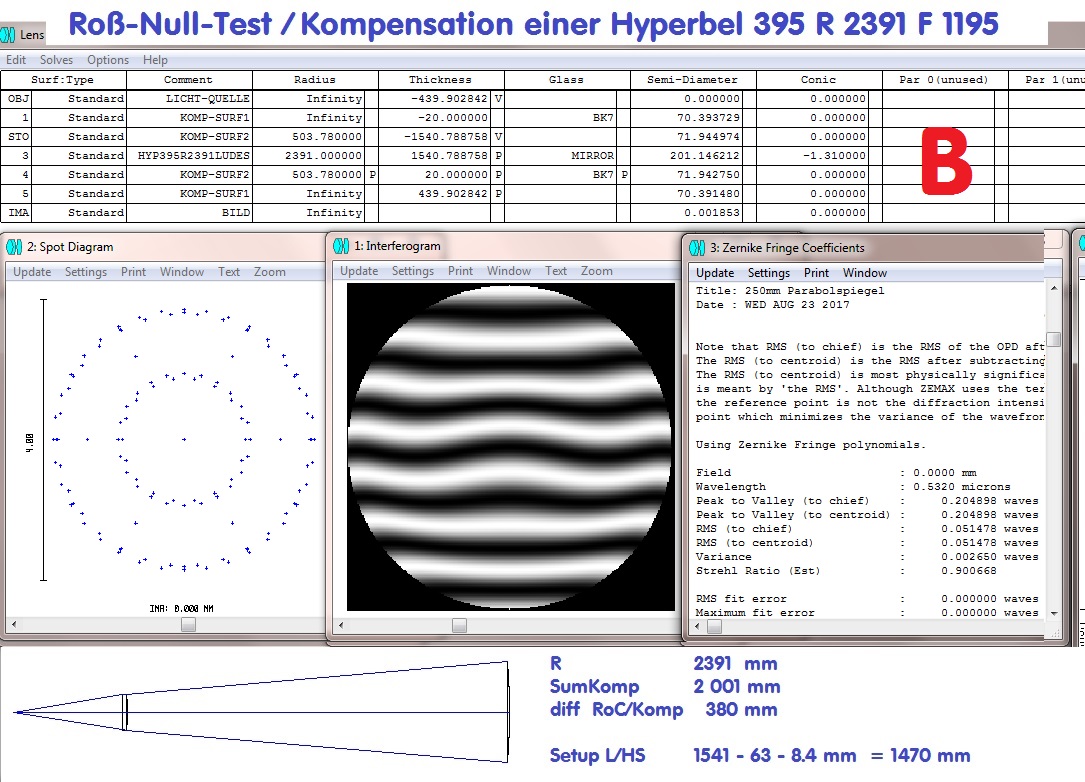
Das folgende Foto zeigt den Testaufbau, wie er sich aus dem oberen ZEMAX-Datenblatt ergibt. 
Versuch einer mathematischen Näherung
Wer kein ZEMAX zur Verfügung hat kann sich auch mit dieser mathematischen Näherung behelfen: Dabei ist zunächst der Graph der
Hyperbel definiert aus Einfallshöhe "h", dem Mittelpunkts-Radius "R" und der konischen Konstante "k". Im Punkt "h" wird an den
Graph eine Tangente und dazu eine Normale gezeichnet/gerechnet. Die Normale in Punkt "h"schneidet die Rotations-Achse (Hyperbo-
loid) in einem größeren Abstand, und so entsteht die gesuchte Schnittweiten-Differenz zwischen dem Mittelpunkts-Strahl und dem
Randstrahlen der Hyperbel. Dieser Abstand läßt sich entweder über den Foucault- oder den Interferometer-Test ausmessen, wie weiter
unten gezeigt wird. Damit läßt sich die tatsächliche konische Konstante des Spiegel mit einiger Sicherheit ermitteln. Die Lösung über
den Ross-Null-Test erscheint mir aber genauer zu sein.
Der Graph dieser Hyperbel (in folgender Zeichnung) definiert sich also über den Mittelpunkts-Radius von 3200 mm und der konischen Kon-
stante von - 1.5 und dem 1/2 Durchmesser von 399.222 mm = "h" = 199.611 . In diesem äußersten Punkt "h" wird eine Tangente gezeichnet
und dazu im gleichen Punkt die Normale, die sich im Beispiel mit einer Differenz von ca. 9.340 . . . mm mit der opt. Achse schneidet. Es soll
also dieser Differenzbetrag ermittelt werden zwischen der opt. Achse und der Normale bei Punkt "h". Diese Näherungs-Rechnung gilt
für alle Kegelschnitte, also Kreis, Ellipse, Hyperbel und Parabel. Siehe auch der Hinweis bei der Parabel -1.0 in der folgenden Übersicht.
(Gelber Kasten)
Die Vermessung über Interferometrie
Es muß also die Schnittweiten-Differenz zwischen Mittelpunkt- und Randstrehlen ermittelt werden. 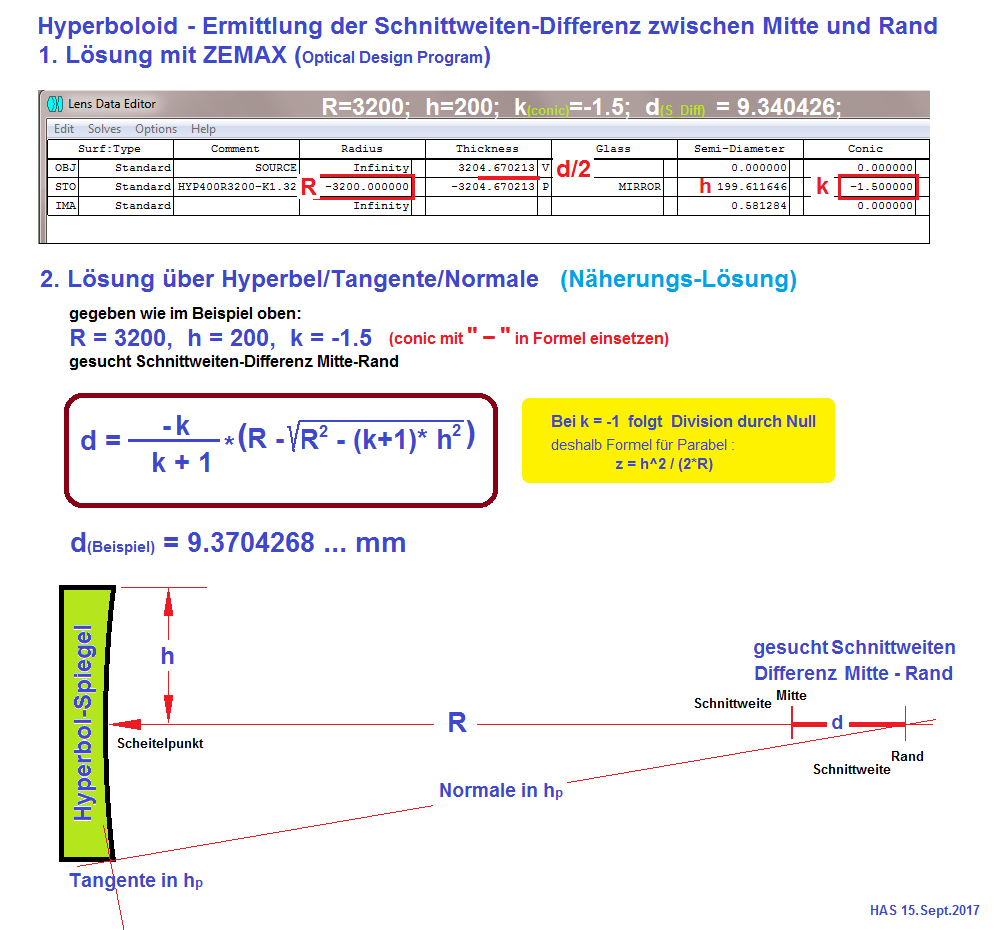
Mit den folgenden Interferogrammen kann man die Abstände ermitteln bei Mitte, 0.707-Zone und Rand. Der obere Bildteil wurde mit ZEMAX
simuliert, der untere Bildteil sind reale Fotos der gleichen Situation. Ein Grenzfall wäre die Parabel mit conic constant -1.0, bei der die Formel lautet:
z = h^2 /(2*Radius) = Formel für Pfeilhöhe der Parabel, gilt auch für Schnittweiten-Differenz der Parabel.
In der jeweiligen Zone erscheinen die mittleren Streifen waagrecht, für die Mitte sind es die Streifen im Zentrum, ebenso bei der 0.707
Zone und schließlich die Streifen am Rand. Am sichersten läßt sich das noch für die Mitte und die 0.707-Zone bestimmen, und dieser
Wert müßte dann mit " 2 " multipliziert werden. Damit kann man zu Beginn die konische Konstante ungefähr eingrenzen.
Ein weitere Möglichkeit ist die Zonen-Abstandmessung über den Foucault-Test, wie er bei Spiegelschleifern üblich ist..
Nachbetrachtung:
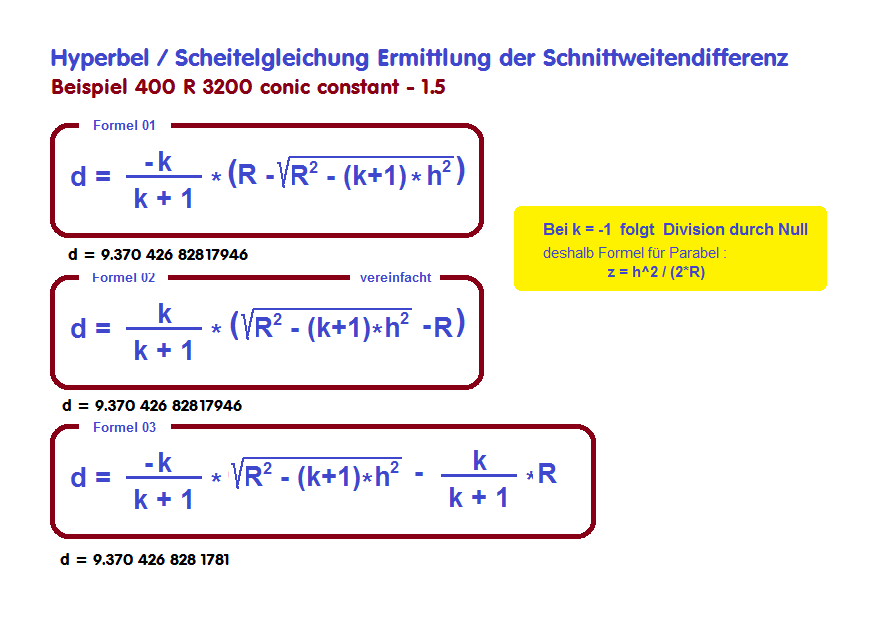
Ein kleines GFA-Programm zur Ermittlung der Schnittweiten-Differenz für die Hyperbel sei hier vorgestellt. Grundlage ist die obere Formel.
Am Beispiel eines Parabol-Spiegels für 400 R 3200 conic= -1.0 ergibt sich
