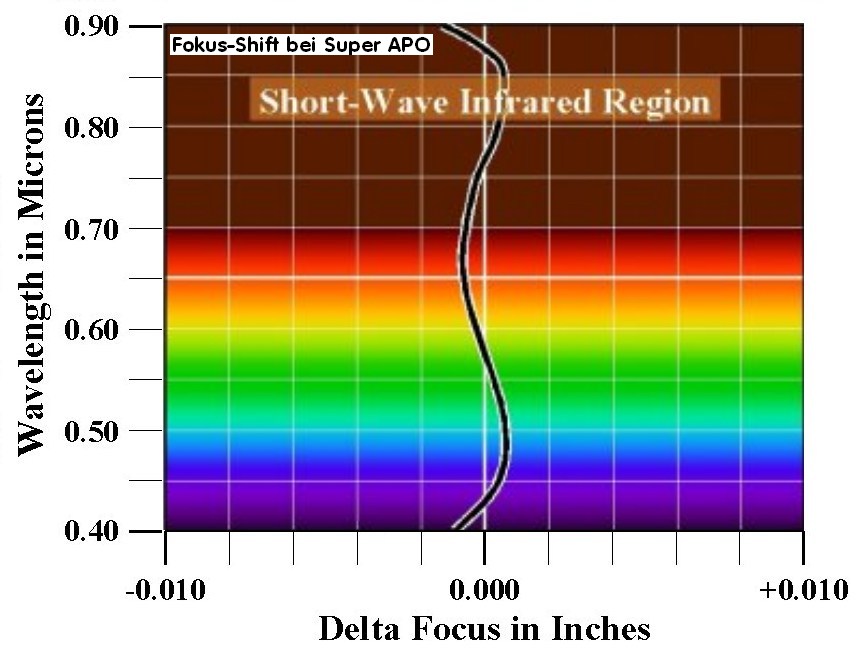
Bei einem Refraktor entscheiden besonders zwei Kriterien über die Farbreinheit eines Astro-Objektivs auf der opt. Achse: Der farbabhängige Öffnungsfehler bzw. Gaußfehler genannt, und der Farblängsfehler, bei dem die Lichtstrahlen der unterschiedlichen Spektren auf der opt. Achse unterschiedliche Schnittweiten haben. Der folgende Beitrag ist eine Sammlung aus vielen vorherigen Berichten, bei dem über die einzelnen farbigen Interferogramm beide Fehler gezeigt werden. Man kann damit ein Diagramm aus Wellenlänge und Strehlwert aufstellen und hätte eine Vergleichsmöglichkeit über die gesamte Bandbreite aller Refraktoren hinsichtlich der Farbreinheit. 

Bei diesem Vergleich muß immer auf die Hauptfarbe Grün als Bezugs-Punkt fokussiert werden. Dann ergibt sich aus der Streifenabkippung der
mittleren Streifen nach unten eine längere Schnittweite für das aktuelle Spektrum, kippen die Streifen hingegen nach oben, würde die Farbschnittweite bzw. Fokuspunkt der betreffenden Farb kürzer bzw. vor der Hauptfarbe Grün liegen.

Achromaten

Über das Diagramm lassen sich die Schnittweiten der Spektralfarben bereits deutlich erkennen: Gelb und Grün haben im besten Fall gleiche Fokuslage, gefolgt von der Schnittweite von Blau und Rot. Alle Achromaten bzw. Zweil-Linser folgen dieser Regel mehr oder weniger deutlich.

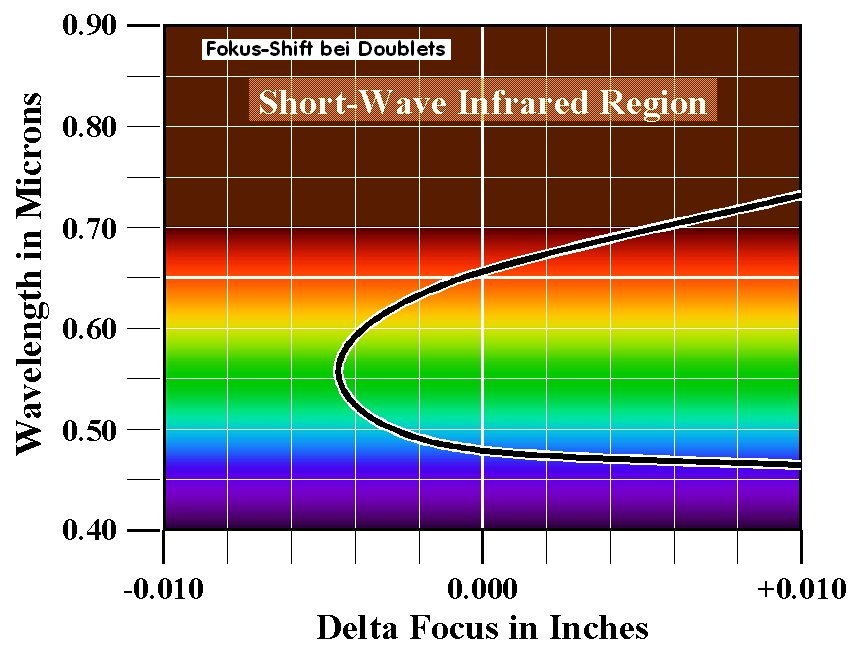
Hier dominiert in jedem Fall der Farblängsfehler vor dem Gaußfehler. In der Regel folgt auf die grüne Schnittweite das gelbe Spektrum und
in einem größeren Abstand Blau und Rot, oft auch umgekehrt. Eindeutig wird dieser Sachverhalt erkennbar über das überdeutliche Abkippen der roten Streifen nach unten bei einer immer gleichbleibenden Interferometer-Einstellung. Daraus ließe sich über die Power-Differenz zu Grün der Schnittweiten-Abstand zu Grün berechnen.

Halb-Apochromaten

Auch bei einem Halb-APO dominiert in der Regel ebenfalls der Farblängsfehler vor dem Gaußfehler, weshalb auch hier die RC_Index-Zahl noch eine gute Beschreibung der Farbsituation abliefert. Zu den Halb -APO's zählen in der Regel alle Zweilinser, ob mit niedrigbrechenden Gläsern oder nicht. Neuere ED-Objektive kommen aber den üblichen Triplets bzw. Voll-APO's erstaunlich nahe, bzw. sind ähnlich farbrein. Beim Vixen ED130SS fällt der Farblängsfehler noch deutlich ins Gewicht vor dem Gaußfehler, wie man in der untersten Reihe des nächsten Bildes eindeutig erkennt.

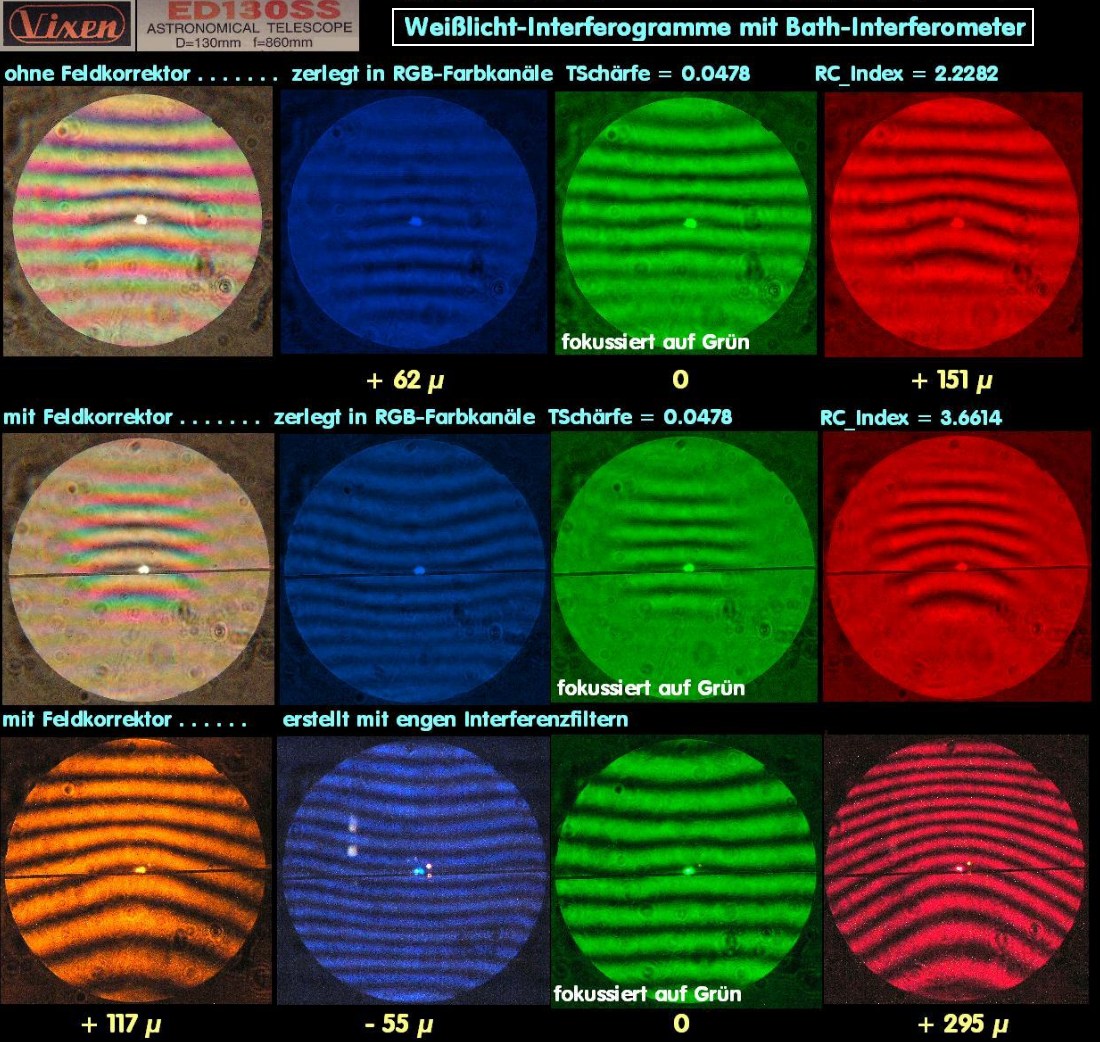
Das obere Vixen ED-Objektiv wäre ein f/6.6 System der SkyWatcher ED ein f/7.5 System ist und deswegen farbreiner erscheint. Würde man das obere Teleskop auf 115 mm abblenden, so dürfte die Farbsituation ähnlich herauskommen.

Apochromaten

Beim Apochromaten sollten drei Spektral-Farben in einem Fokus vereinigt werden. Jetzt bekommt aber der farbabhängige Öffnungsfehler im Vergleich zum Farblängsfehler ein größeres Gewicht und jetzt läßt sich eine exakte Trennung der Qualität nur noch über den Strehl-Wert treffen, der sowohl den Gaußfehler über die sphärische Aberration, aber auch den Farblängsfehler über die Power enthält und damit vergleichbar wird. Kommen jedoch weitere Fertigungs-Fehler hinzu, wie tendenzielle Überkorrektur, Astigmatismus oder Koma (= Zentrierfehler) so wird ein Vergleich zusätzlich erschwert.

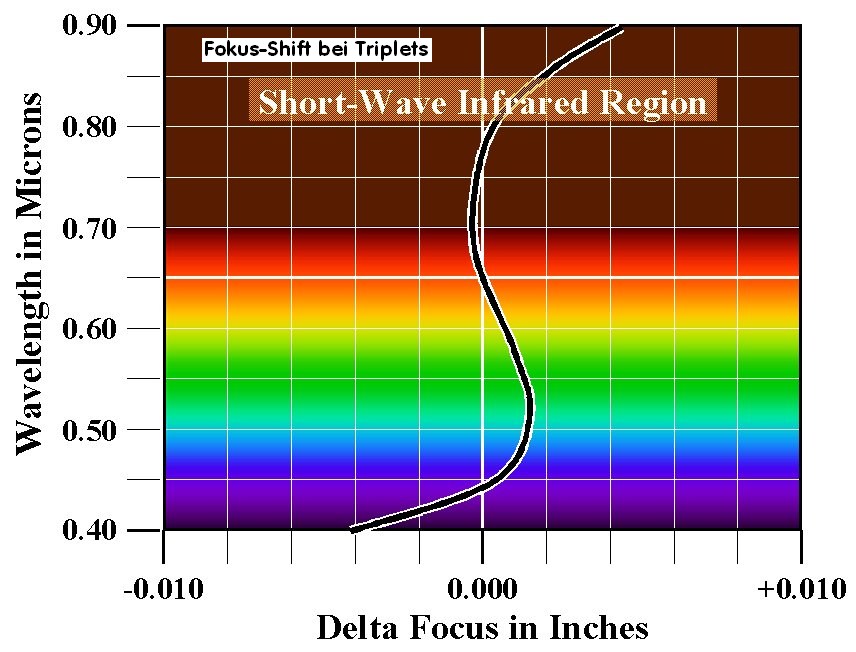
Betrachtet man dieses Triplet isoliert über den Farblängsfehler, so hätte man einen APO vor sich mit einem RC_Indexwert von 0.8883. Neben einem Zentrierfehler in Form von Achskoma sieht man den IGrammen eine tendenzielle Überkorrektur an, was zu Einbußen führt, wenn man das Teleskop visuell nutzen möchte. Für die Fotografie wäre dieser Refraktor eine gute Wahl.

Über die RC-Indexzahl wäre der Apolar von TAL gerade noch ein APO, allerdings mit einem kaum wahrnehmbaren Gaußfehler. Leider trübt bei diesem Teleskop ein Öffnungsfehler höherer Ordnung den guten Eindruck, eine Verkippung des mittleren Triplets sorgt hier ebenfalls für einen Zentrierfehler.

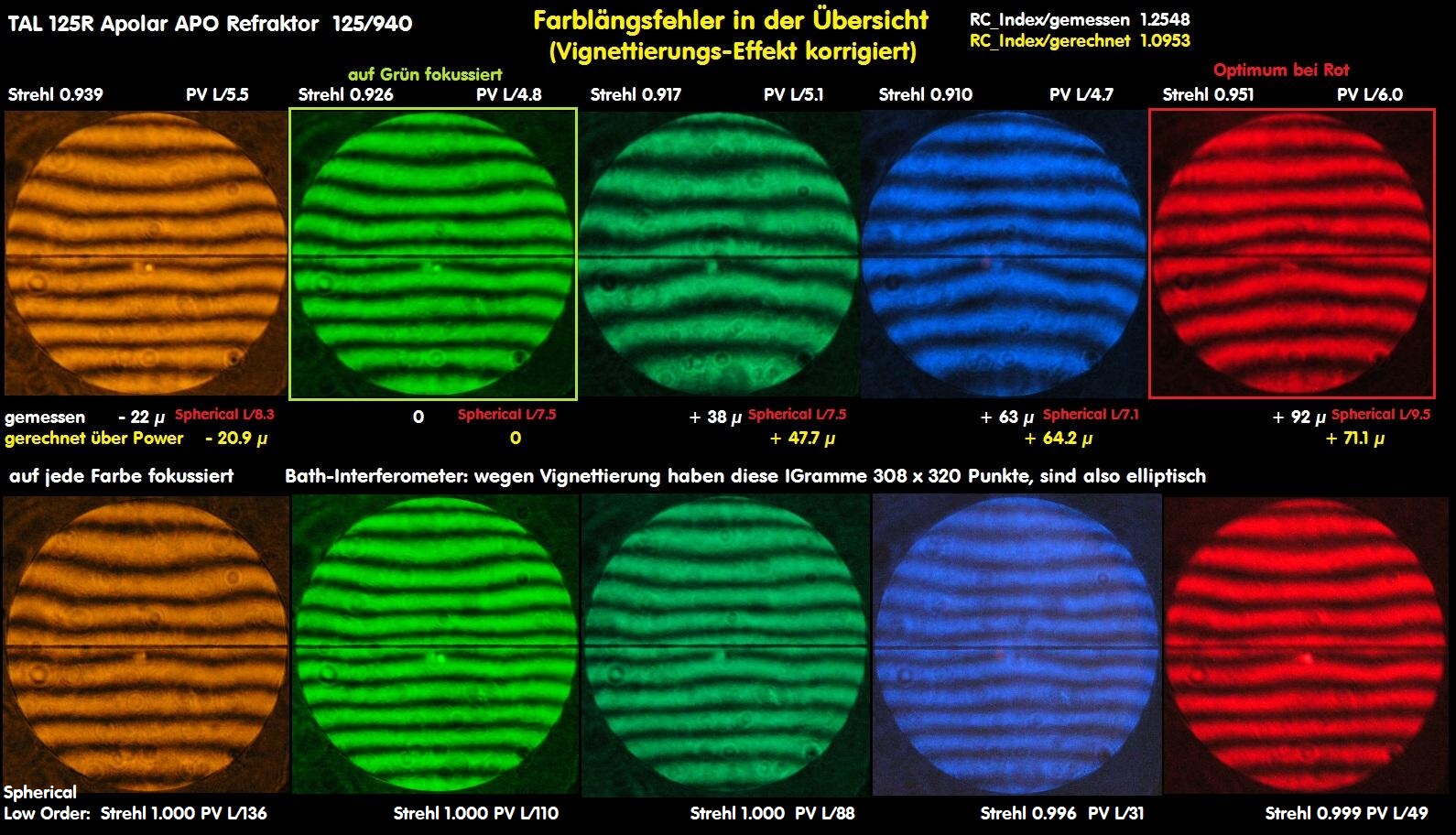
Während die RC_Indexzahl auf einen sehr farbreinen APO hindeutet, liegt bei folgender Optik ein ausgeprägter Gaußfehler vor mit einer deutlichen Unterkorrektur im roten Spektrum und eine ebenso deutlichen Überkorrektur im kurzen Spektrum.

Obwohl es ein f/7.5 Zweilinser ist, wäre der Gaußfehler noch sehr moderat, was man über die Strehl- und PV-Werte erkennen kann.

Beim nächsten Objektiv wäre die Größe des Gaußfehlers über den PV-Wert abzulesen ( PV L/5.3 für Blau und PV L/6 für Rot), da auf jede Farbe einzeln fokussiert worden ist.

Bei einem f/6 System muß man auch mit einem größeren Gaußfehler rechnen. Dieser wiederum läßt sich bereits über das Foucault-Bild links oben dokumentieren über die sichelförmige Farbverteilung und später über die eindeutigen Ronchi-Bilder.

Der geringe Gauß- und Farblängsfehler bei diesem f/8 System führt zu einem sehr farbreinen Objektiv.

--------------------------------------------------------------------------------

Eine andere Art, die Farbreinheit von Objektiven einzuschätzen bieten der Ronchi- und Foucault-Test:  Refractor Optical Performance Results
RonchiGramme Foucault-Bilder
siehe auch diese Übersicht: je deutlicher die Farben über eine senkrechte mittlere Achse voneinander getrennt sind, umso stärker tendiert ein Refraktor zum Achromaten. Je stärker die Farben sichelförmig verteilt sind und je weißlicher der Gesamteindruck ist, umso deutlicher tendiert ein Objektiv in Richtung APO.

--------------------------------------------------------------------------------

In diesem Zusammenhang ist auch die Frage interessant, wie exakt eine Umrechnung des Farblängsfehlers über die
Power-> Pfeilhöhen-Formel tatsächlich ist. Es spielt im Bereich 3-5 Mikron.

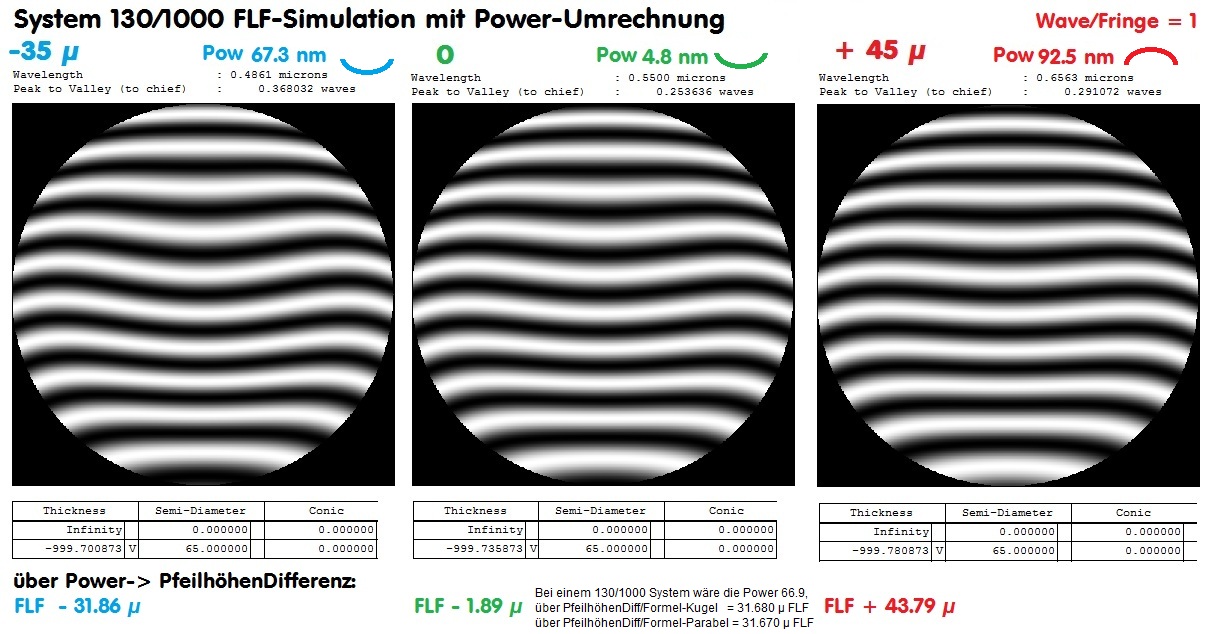
Zunächst kann man über eine ZEMAX-Simulation bei einem 130/1000 mm Objektiv (TOA von Takahashi) einen Gaußfehler von ca. PV L/4 einführen, erzeugt ein Fokus-Shift von hier 35 Mikron für Blau = 486.1 nm wave und läßt sich für diese Farbe das dazu passende Interferogramm zeichnen.  Alternativ dazu ein Fokus-Shift in die andere Richtung, also für Rot von 45 Mikron Fokus-Shift von der Hauptfarbe Grün entfernt. Wie exakt läßt  eine sich anschließende Auswertung über AtmosFringe die urspüringlich von ZEMAX eingesetzten Fokus-Shift-Werte über die Power-Werte wieder  auf die ursprünglichen Farblängsfehler-Werte von - 35µ bzw. + 45µ treffen.  (Dabei ist die Annahme, daß sowohl ZEMAX wie AtmosFringe richtig rechnen, ebenso ungesichert, wie das Problem, daß man beim Einlesen des Interferogrammes in Atmosfringe exakt den richtigen Umkreis findet und daß bereits ein Punkt-Versatz von nur einem Pixel bereits Abweichungen im Bereich bis 2 Mikron erzeugen kann) Das wurde in der zweiten Übersicht untersucht. Mit Gauß- und Farblängsfehler entsteht in diesem Beispiel bei Blau eine Differenz von - 3.14 µ zwischen ZEMAX und Atmosfringe, bei Rot wäre die  Differenz 1.29 µ. Beide Ergebnisse haben eine Streuuung. Selbst bei der Hauptfarbe Grün entsteht eine Streuung im Bereich des Nullpunktes. Die  Power-Abweichung nach oben bzw. unten ist durch "Bögen" gekennzeichnet.

Diesmal wird nur der Farblängsfehler simuliert, also ohne Gaußfehler, was die Auswertung eventuell sicherer machen könnte. Nun wären es bei Blau - 20µ Differenz, laut ZEMAX, und für Rot + 40 µ Differenz, wieder nach ZEMAX. Nun kann man sich allein auf die Streuung konzentrieren bei Blau von 2.32 µ und bei Rot eine Streuung von 3.15µ, während selbst beim Nullpunkt = Grün noch eine Streuung feststellbar ist.

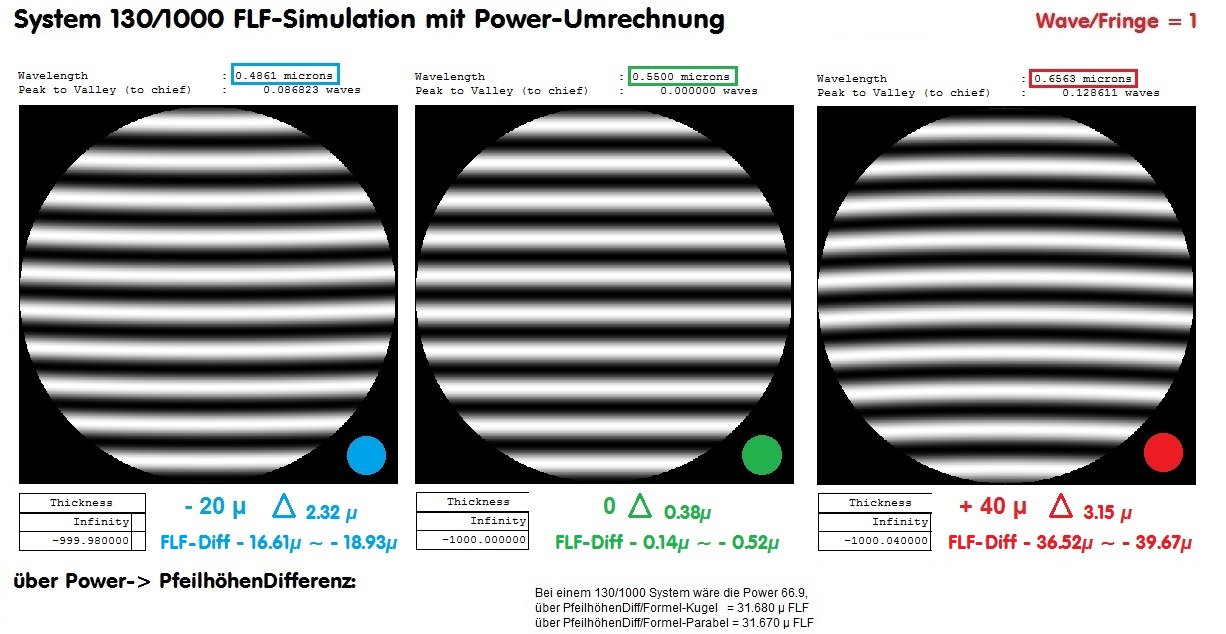
Zumindest diese Beispiele zeigen, daß
01. der über die Power ermittelte Farblängsfehler bei diesen ZEMAX-generierten Beispielen immer kleiner ist, als der ZEMAX-Wert selbst,
02. auch über den Weg ZEAMX->AtmosFringe eine Unschärfe von ca. 5µ nicht zu vermeiden ist.
03. Diese Unschärfe hängt vermutlich mit der schlechten Reproduzierbarkeit beim Einlesen von Interferogrammen zusammen, da Umkreis  und Punktlinien variieren können, also nicht immer an die gleiche Position gesetzt werden.
04. diese Unschärfe auch für die "normale" Auswertung von Interferogrammen allein durch AtmosFringe oder einem anderen Auswert-Programm angenommen werden kann.
05. deshalb auch der daraus ermittelte RC_Index eine Streubreite haben muß. Im Berechnungs-Algorhytmus wird die Pfeilhöhenformel der Parabel benutzt. Nimmt man die Pfeilhöhen-Formel für die Kugel, so bleibt die  Differenz weit unter einem Mikron, wie ebenfalls untersucht wurde.