F079 Kompensations-Linsen für Ross-Null-Test
-
Von elliptisch, parabolisch bis hyperbolische Spiegel lassen sich mit Hilfe von sog. Ross-Null-Linsen
herstellen. Es ist ein relativer Null-Test, der nur stimmt, wenn die Abstände zwischen Linse und Spiegel
genau stimmen. Dann aber lassen sich alle Standard-Tests machen, wie man sie von der Herstellung von
Kugelspiegeln kennt. Die erste Linse hätte eine geringe Überkorrektur, die sich jedoch rechnerisch über
eine konische Konstante auf der 2. Linsenfläche kompensieren läßt. Entscheidend wäre die Homogenität
der Gesamtfläche. Insgesamt wird die Überkorrektur der Parabel im Krümmungsmittelpunkt durch die
Unterkorrektur der Linse auf Null-Kompensiert. Sinnvoll in diesem Fall ist ein Gegentest, entweder am
Himmel selbst, oder gegen einen Planspiegel bzw. Flüssigkeitsoberfläche.
Hier zunächst das Zygo-Certifikat

Die Linse in der Halterung: Planseite zur Lichtquelle

Konvexseite zum Parabolspiegel

Zwei Rechenbeispiele: ein Galaxy 504 R 8032 Newton also f/5
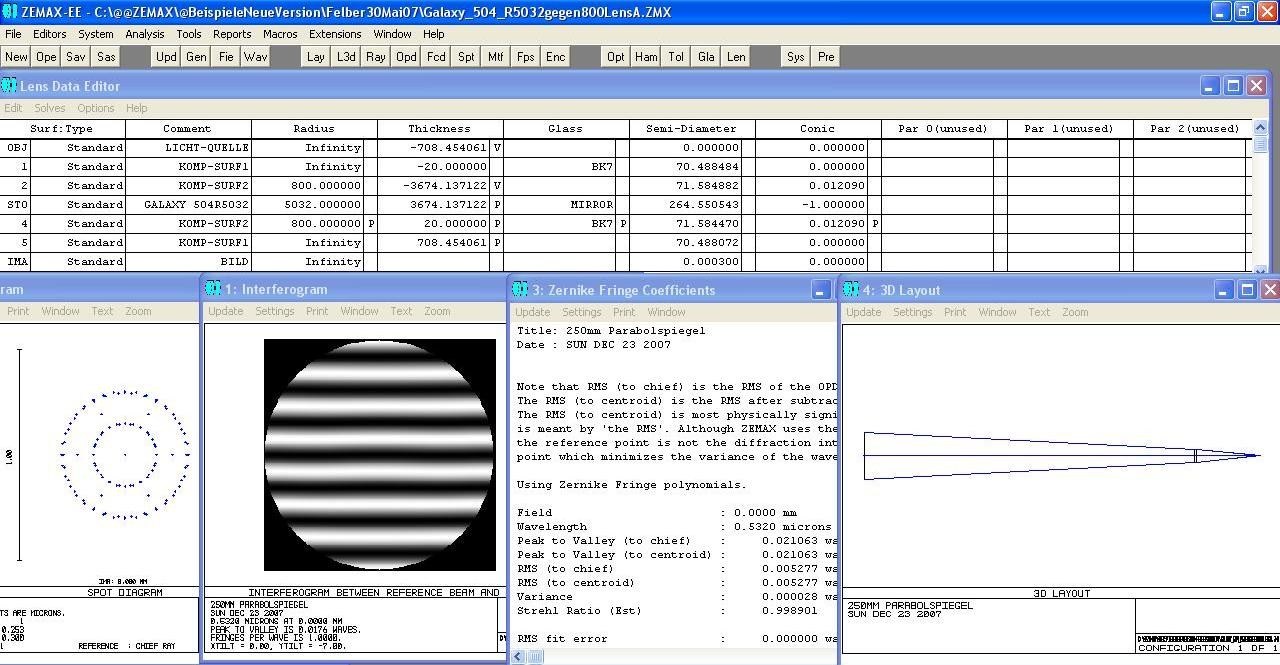
Und ein Alluna-Spiegel (mein eigener) 506 R 4054 also ein f/4 Newton
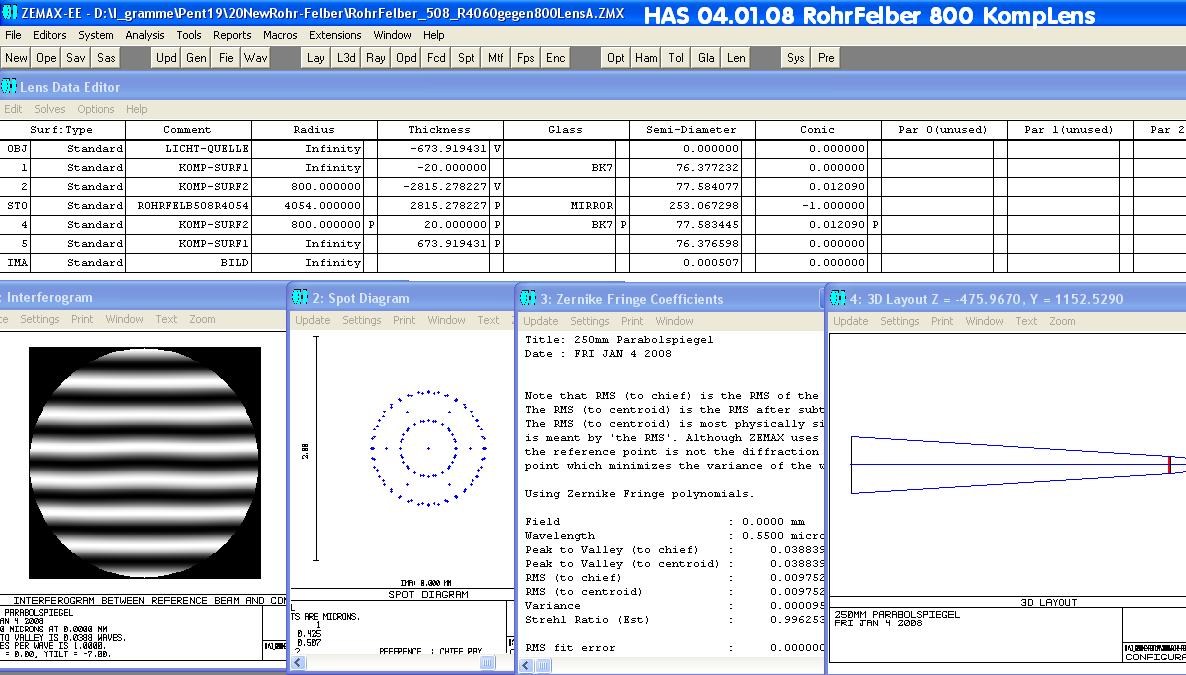
eine zweite Big Lens für Kompensation: das Certificate
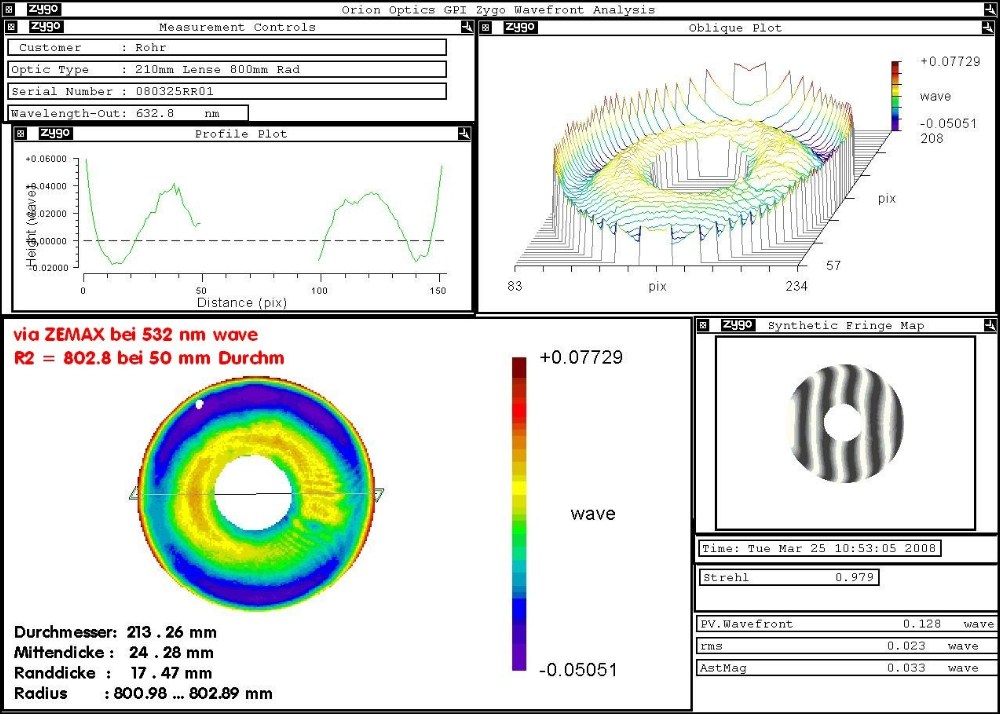
und die Linse in der Halterung.

Damit lassen sich große Spiegel auch herstellen, wenn kein adäquader Planspiegel vorhanden ist. Die Gegen-
kontrolle am Himmel ist jedoch immer empfehlenswert, z,B, am Polarstern. -
Hallo Wolfgang,
Von elliptisch, parabolisch bis hyperbolische, lassen sich Spiegel mit Hilfe von sog. Ross-Null-Linsen herstellen.Von elliptisch, parabolisch bis hyperbolische Spiegel lassen sich mit Hilfe von sog. Ross-Null-Linsen
herstellen.
Ist der Satz so richtig verstanden?
Gruß Günterwww.g2-Astronomie.de
GSO 12" Dobson, C8-Orange, C8-Schmidtkamera, Comet-Catcher, LW125/1300, MC100/1000, Skywatcher ED 80 PRO, Skywatcher 8" Dobson, Skywatcher Maksutov SKM 127 / 1500 -
Hallo Günter,
ceravolo.com/ross_null.pdf
in diesem Artikel von Ceravolo ist der Unterschied zwischen Dall-Null- und Ross-Null-Test beschrieben.
Grundsätzlich wird immer eine plankonvex-Linse zur Kompensation von Kegelschnitt-Rotations-Flächen
benutzt: Und das sind Ellipse, Parabel, Hyperbel. Es ginge jedoch genauso gut ein Kugelspiegel, aber mit
dem Nachteil, daß man im Strahlengang messen muß. astro-foren.de/showthread.php?p=35277#post35277

Liest man den Bericht von Ceravolo, wie im oberen Link, dann wird eine relativ kleine Linse nur ein Mal im
Strahlengang benutzt. Beim Ross-Null-Test hingegen ist man exakt auf der Achse und der Strahlengang
geht zweimal durch die Linse. Entsprechend genau muß die benutzte Linse sein.
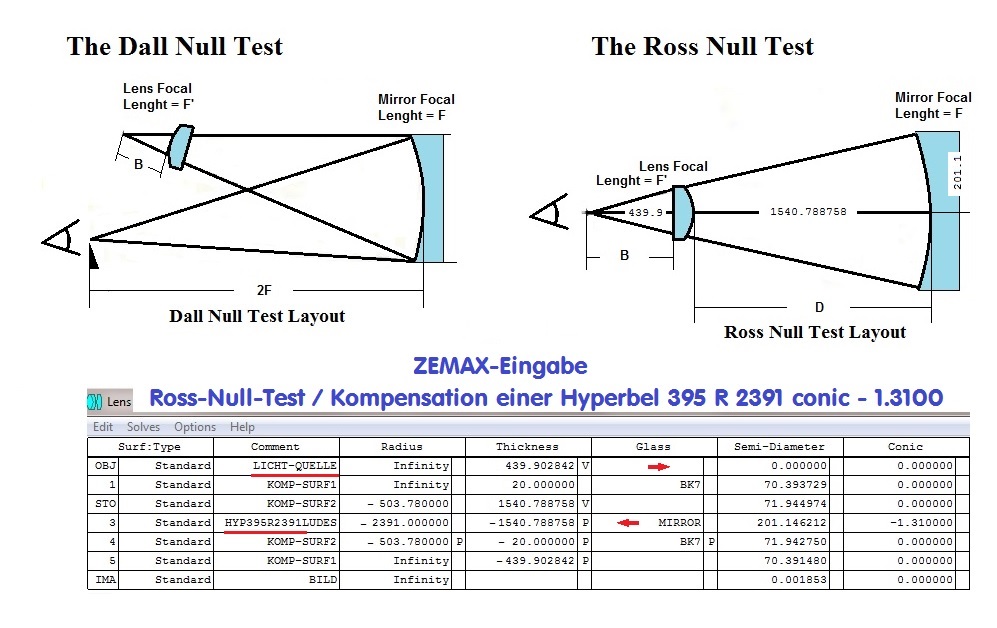
Nun kann man sich die Sache so vorstellen:
Ausgehend von einer perfekten Sphäre - was ein perfekter Kugelspiegel ist - wird bei der Vertiefung der
Mitte langsam ein Rotations-Ellipsoid daraus, was man noch im 2. Brennpunkt der Ellipse auf Null prüfen könnte, so wie
die Sphäre. Beim Rotations-Paraboloid geht das nicht mehr. Das wäre bei einem f/4 Parabols-Spiegel schon heftig
überkorrigiert. Setzt man nun die Ross-Null-Linse mit der Konvex-Fläche zum Spiegel ein, und zwar
beginnend von der Lichtquelle im Krümmungsmittelpunkt (also der Radius auf der opt. Achse, nicht am
Rand !!!) dann nimmt die Überkorrektur allmählich ab, je näher man die Linse an den Spiegel schiebt, bis
sich wieder eine Null-Situation ergibt. Über diesen Punkt hinaus ergibt sich dann allmählich die
Unterkorrektur. Dieser Test ist also nicht absolut, wie der Test am Himmel oder gegen einen
Autokollimations-Planspiegel, sondern variabel und damit abhängig vom richtigen Abstand Lichtquelle - Linse - NewtonSpiegel.
Bei RC-Systemen hat man aber sogar einen hyperbolischen Spiegel, dessen Mitte noch tiefer liegt, der also,
aus dem Krümmungsmittelpunkt betrachtet noch stärker überkorrigiert ist als Ellipse, später Parabel und
noch später Hyperbel. Auch hier kann die gleiche Plankonve-Linse die Überkorrektur auf Null kompensieren,
nur rückt sie noch näher an den Hyperbol-Spiegel.
Mit Zemax, oder Oslo oder Atmos lassen sich die genauen Abstände relativ leicht berechnen. Man muß aber
schon sehr zuverlässig die genauen Linsendaten haben, die Abstände und über die Glassorte den Brechungs-
Index. Auch ein Certifikat über die Genauigkeit der Linse ist hilfreich.
Und dann muß man die Sache wenigstens einmal "eichen", also unbedingt die Gegenkontrolle am Himmel
oder gegen einen Planspiegel, und wenn dann jedes Mal ein exakter Null-Test herauskommt, dann stimmt
der Ort der Linse und damit auch die opt. Daten der Linse selbst und man ist sehr flexibel bei der Prüfung
von Kegelschnittflächen. -
Some notes to a compensation setup:
First:
This setup is calculated for a green laser module with
532 nm wave. You must use monochromatic light !!!
Because the biconvex lens causes a big color spectrum.
To figure a parabola as a null test, you can use the sky with a parallel light beam, or you use a autocollimation
flat in double pass, or you test in RoC (Radius of Curvature) and for this case, the parabola looks extremly overcorrected.
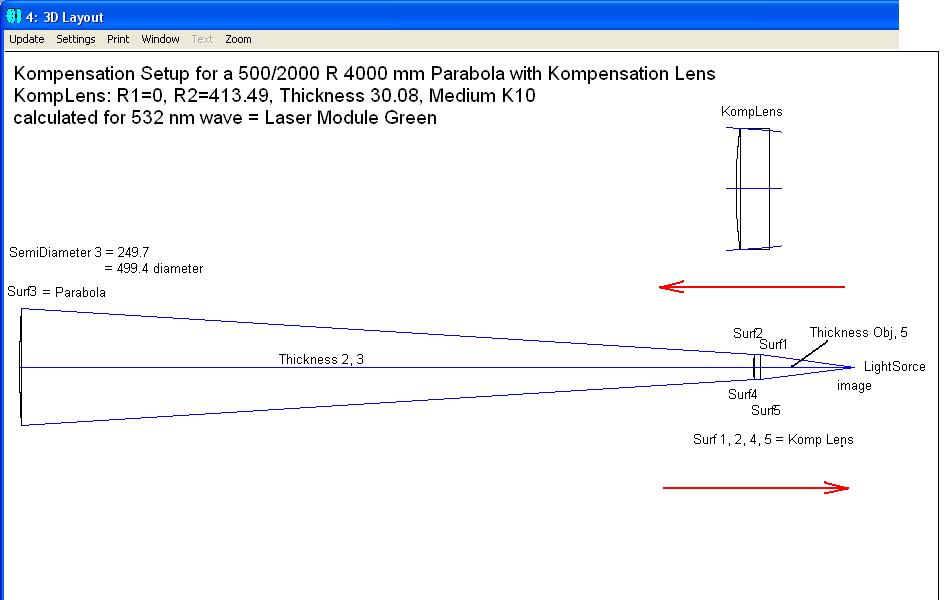
This overcorrection you can compensate with a planconvex lens with the convex surface to the parabola as the scetch shows.
You can calculate this setup with any optical design program, and you start with a light sorce at the right.
Then the light passes the Surf 1 of the lens (flat) Surf 2 of it (convex) . After it the light is reflected from the parabola mirror
and it comes back to the convex surf of the lens, it passes the flat lens surface and at last at the focal plane of this setup.
At a definite distance this kompensation lens compensates the overcorrection of the parabola and so we
get a Null test, if the lens data are OK, and we insert the correct parabola data.
Very important is the wave lenght of that setup and very important the medium refracting index numbers for the
wavelenght of 532 nm wave. If all OK, then this Setup should work.
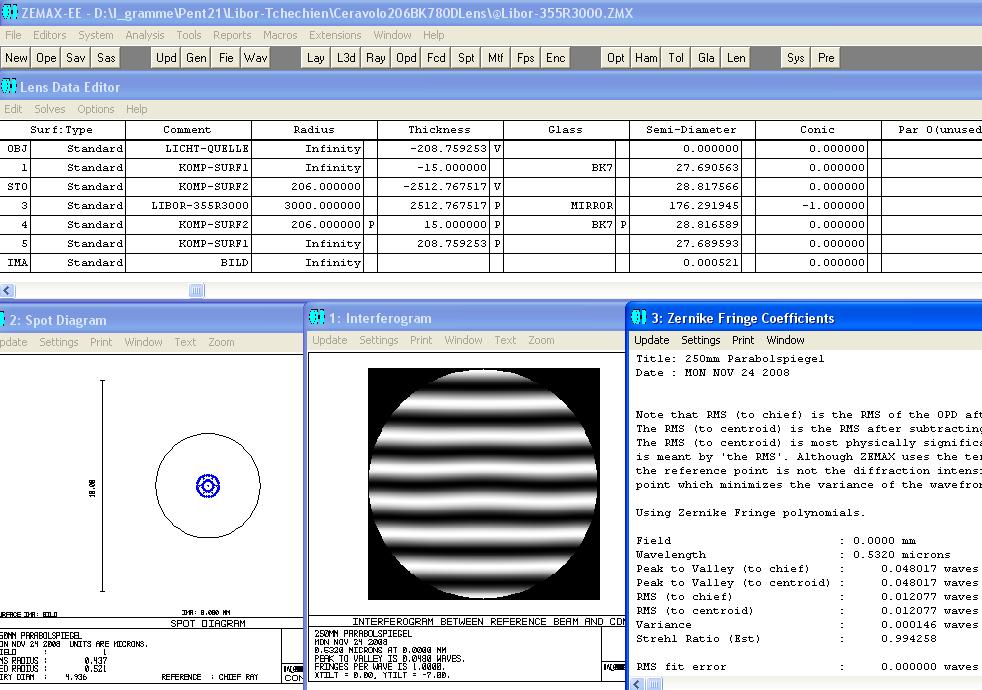
This scetch explains the next data map of ZEMAX.
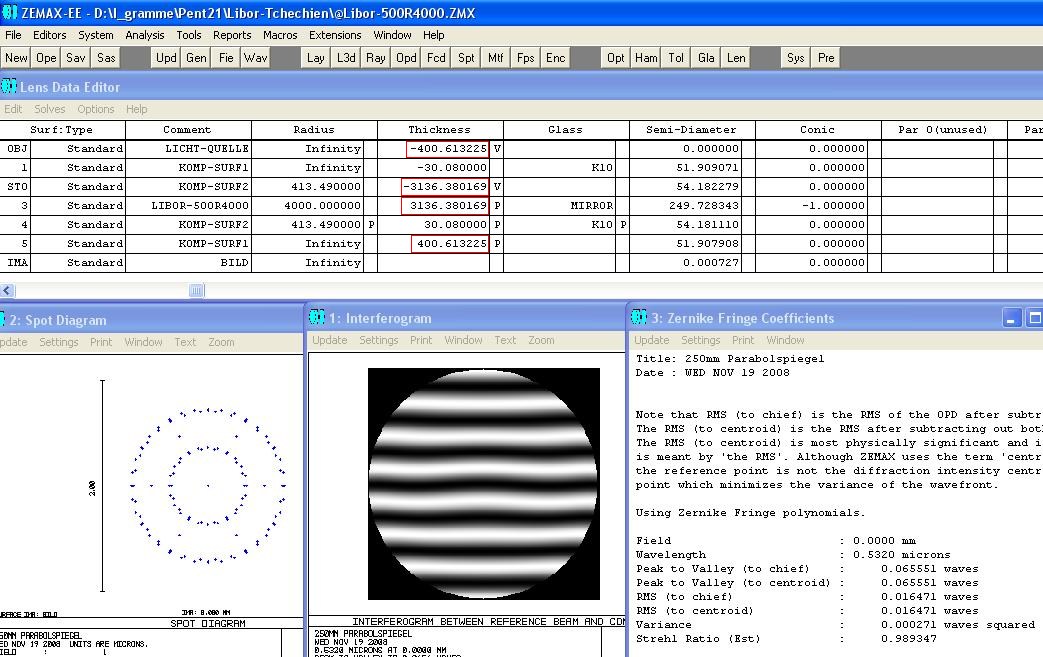
This map shows you the accuracy of this setup: It's under the Airy disc.
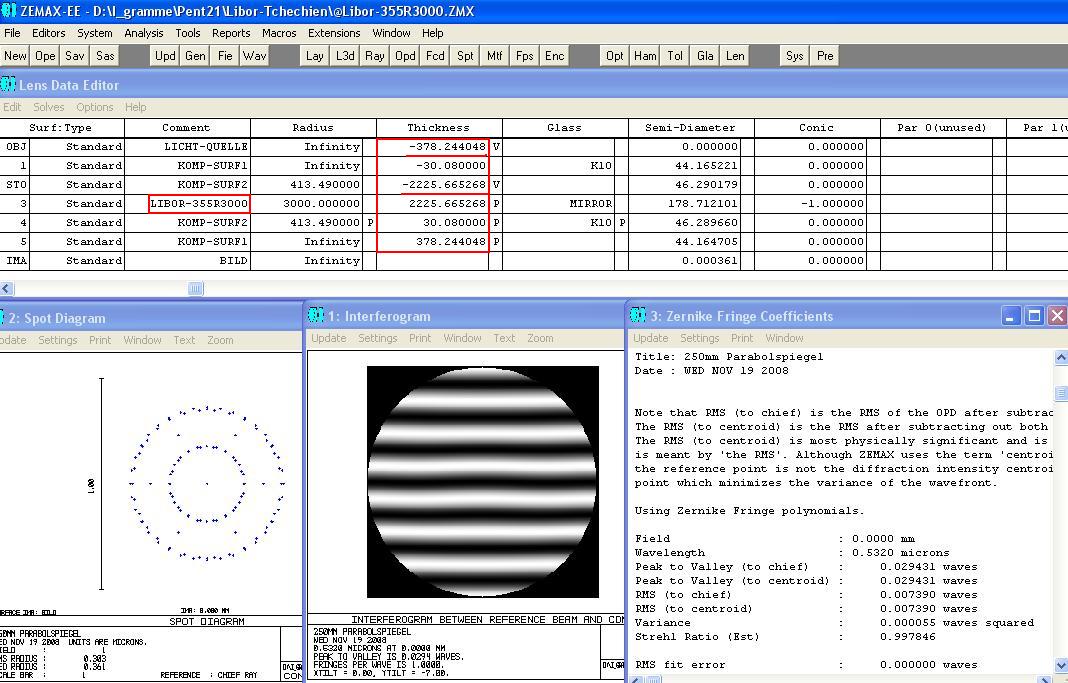
Weitere Beispiele:
===============================================
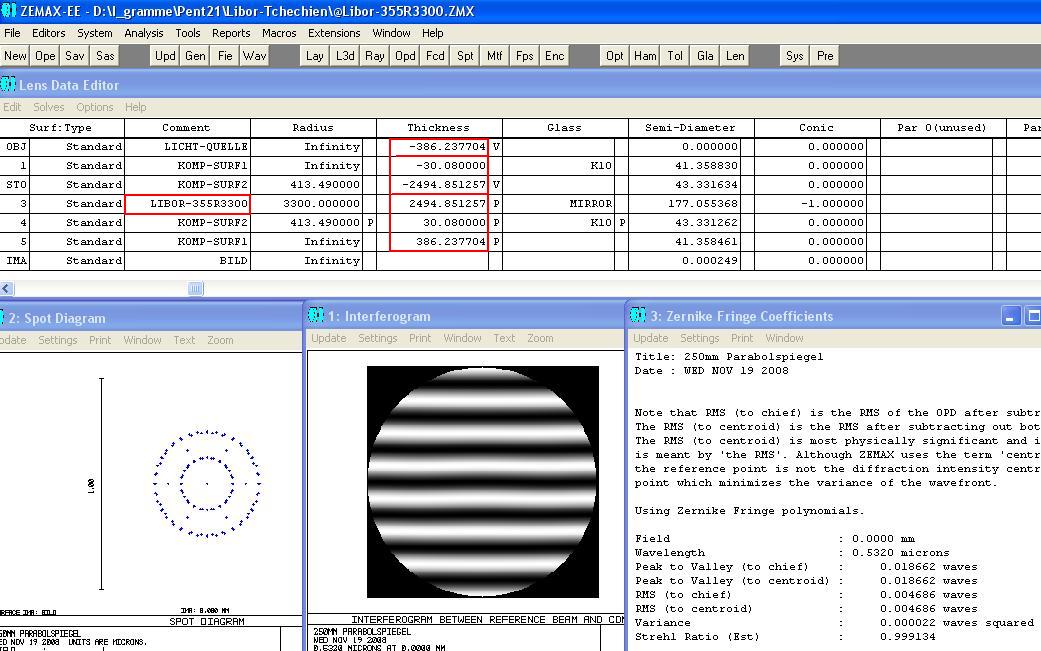
===============================================
-
ceravolo.com/ross_null.htm
Ceravolo Ross Null Lens for Mirror Testing
</CENTER> The COS Ross null lens.
The COS Ross null lens.
Using your Ronchi or Foucault tester, the Ross null lens allows you to test your parabolic, elliptical or hyperbolic telescope primary mirror at the center of curvature as though it were a sphere. There is no need to interpret difficult shadow measurements because figure irregularities like bumps, holes and zones are easy to see and interpret. That's half the battle when producing a truly fine primary mirror. The Ross null test has been used to make very smooth mirrors with a 1/20th wave peak to valley surface quality. The result: high contrast images of the planets and deep sky objects.
 The Ross null lens is placed ahead of the mirror's center of curvature.
The Ross null lens is placed ahead of the mirror's center of curvature.
The Ceravolo Ross null lens is recommended for mirrors up to 20” diameter. Up to this size an f/4 mirror can be tested to 1/20th wave surface quality. Larger mirrors can be tested as long as they are slower than f/4, for example a 30” f/5 Newtonian primary.
Determining the required null lens - mirror spacings for your set up has been made easy by the efforts of Douglas George of Diffraction Limited. Over ten years ago Doug wrote a small program that calculated the spacings required for the Ross null test. Recently, James Lerch updated the old DOS software so it will run reliably in the Windows XP Operating System.
Download the free Ross null test software. Many thanks to Doug and James for providing this service to the community!
In order to test telescope primary mirrors at the center of curvature with an interferometer, a null test must be used. The Ross null lens is ideal for the application as it avoids the expense of a large optical flat. To learn how to perform mirror testing with the Ross null lens, download the PDF document, "Using the Ross Null Test".
Ross null lens specifications
Diameter: 80 mm
R1: 206mm convex
R2: flat
Thickness: 15 mm
Substrate: BK7
Surface quality 1/10th wave or better on both sides. A Zygo interferometer printout is supplied with each serialized Ross null lens.
Price USD $575.00 + shipping and handling.
We accept personal checks (from customers in Canada and the U.S. only) as well as VISA. For VISA transactions add a 3% transaction fee. All payments to be made in USD.

For this type of lens I calculated the Ross-Null-setup for a parabola 355/1500 R = 3000 with a BK7 lens
and the upper spezifications. From the diameter of 80 mm you just need 2*28 = 56 mm diameter. This
lens with the certificated accuracy is expensive and I would try it at first with an achromatic lens from
a binocular with the convex radius to the mirror. This would be cheaper. The easiest way is, you grind a
spherical mirror at first, then put the lens between light source and mirror at a position, there you get
the opposite undercorrection of the parabola, and then you refigure the mirror to null. At last you should
get a perfect parabola.
A setup for a f/3.5 mirror:
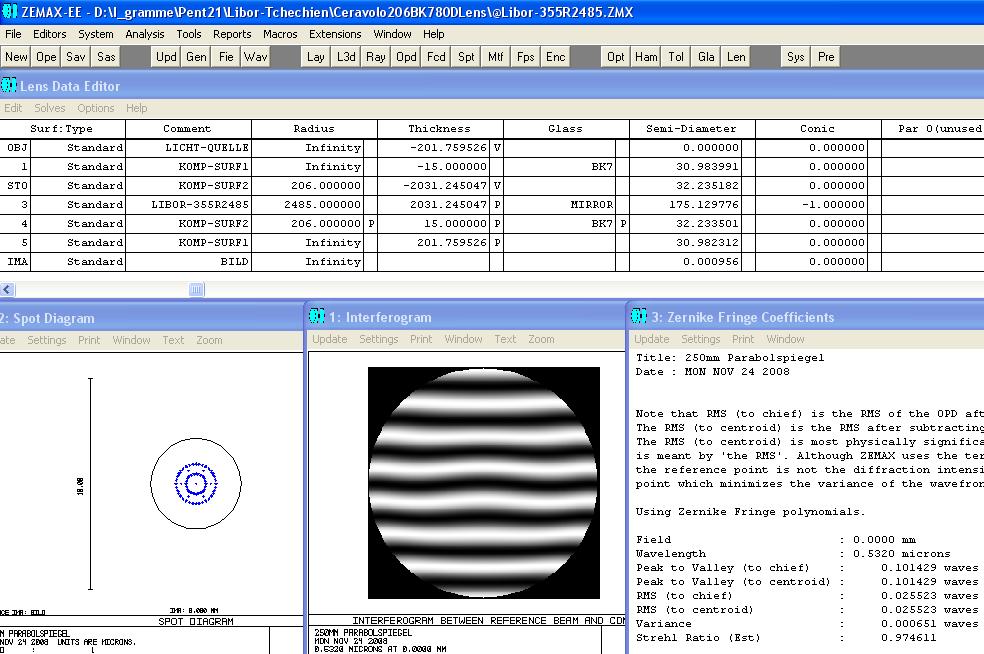
-
hello Wolfgang,
can you making a simulation whith zemax for a miror of 600mmf/d3.5 please whit P . ceravolo lenses.
thanks -
Hello Franck,
For this size and this ratio the Ceravolo lens is to small, you must use a bigger one or a spherical mirror.
The accuracy of this system is to low: Strehl = 0.8183 and the spotdiagramm bigger than the Airy disc,
and this setup shows undercorrection. The lens size should be 160 mm and the radius about 500 mm.
You also can use a spherical mirror, this is much cheaper. Look here: astro-foren.de/showthread.php?p=35277#post35277