F055 Sphärometer - Pfeilhöhe bestimmen bei Kugel & Parabel
17.07.2005 Sphärometer - Pfeilhöhe bestimmen (Siehe auch http://rohr.aiax.de/Power1.jpg)
Bei manchen Beiträgen, die man auf bestimmten Astronomie-Foren trifft, hat man
den Eindruck, daß manches Wissen in Vergessenheit geraten ist, zumal das
kleine Buch von Kurt Wenske SuW Taschenbuch Nr. 7 Spiegeloptik, so gut wie
nie in den Beiträgen zitiert wird. Die Lektüre kann ich nur empfehlen.

Im vorliegenden Fall werden naßforsch Bilder von einem "Spherometer" (http://makeashorterlink.com/?N2225327B) veröf-
fentlicht, die überhaupt nicht mehr nachvollziehen lassen, ob der Autor dieses
geistigen Gedankengutes überhaupt weiß, wie er damit richtig umgeht.
Zur Unterstützung derartiger Schmalspur-Veröffentlichungen die Formeln und
anschließend ein paar Bilder, wobei die in der Industrie verwendete Meß-
technik zur Radien-Messung hier nicht beschrieben werden soll - weil eine
Anwendung aus dem Amateur-Bereich.

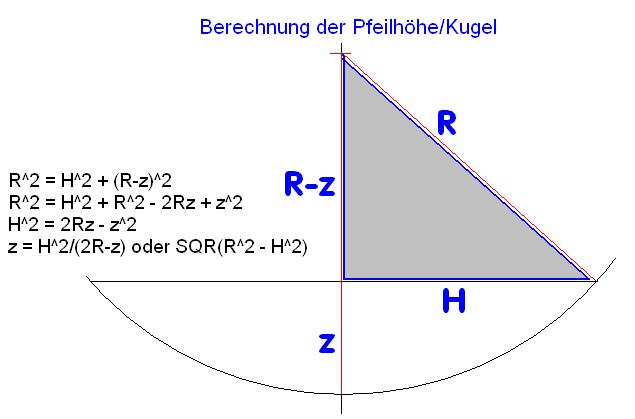
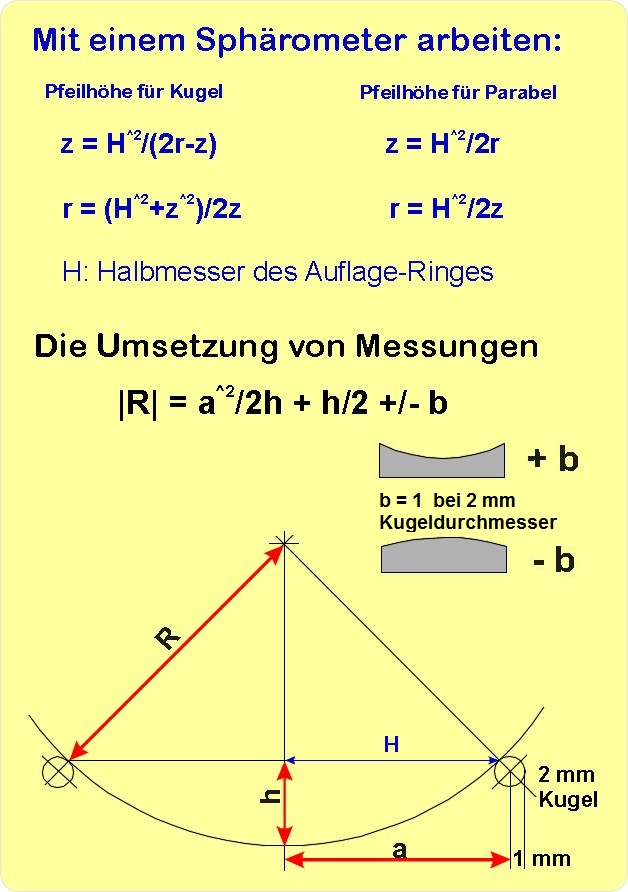
In oberer Darstellung ist in der allgemeinen Darstellung die Pfeilhöhe mit z bezeichnet, siehe
bei Wenske, SpiegelOptik SuW, Taschenbuch Nr. 7, Vehrenberg-Verlag 1978, 2. Auflage, und
die Einfallshöhe mit H, während wir intern unten für die Pfeilhöhe "h" und "a" verwendeten.
Das ist nur eine andere Form der Darstellung, von der man sich nicht verwirren lassen möge.
Um Radien exakt messen zu können, muß entweder über eine scharfe Kante
der Durchmesser des Meß-Auflage-Ringes bekannt sein, oder man geht gleich
auf die 3-Punkt-Kugelmethode über, die eine exakte Auflage garantieren. Auch
bei diesem Meßverfahren ist eine Differenzmessung über einen exakt bekannten
Radius genauer, als über die Ermittlung der Pfeilhöhe, auch noch bei Verwendung
einer tausendstel Meßuhr nicht exakt genug. Man merkt es spätestens, wenn
man mit Foucault einen Radius ausmißt. Auf dem Bild sieht man die 2mm Stahl-
Kugeln, die in eine exakt definierte Ring-Nut eingeklebt sind.

Eine tausendstel Meßuhr liefert etwas genauere Meßwerte ab, in diesem Fall
spielen aber bereits die richtige Temperatur und zuviel/zuwenig Auflagedruck
eine Rolle.


Beispiel 16 inch Zeiss Cassegrain 04.Nov.2018
Bei mir wurde ein 16 inch Zeiss Cassegrain angeliefert, leider ohne irgendwelche optische Daten. Während der Radius des
parabolischen Hauptspiegel noch relativ einfach in RoC oder in Autokollimation ermittelt werden kann, braucht man für einen
hyperbolischen Konvexpiegel (beim klassischen Cassegrain) einen Spherometer - leider muß man hier mit einer gestimmten
Toleranz rechnen, Selbst bei Verwendung einer 0.001 Digitalen Meßuhr. Die Arbeitsschritte sind also:
- Radius des Sekundär-Spiegels ermitteln
- Radius des Hauptspiegels ermitteln
- Berechnung des wahrscheinlichen Cassegrain-Systems mittels ZEMAX oder ein Strahlendurchrechnungs-Programmes
- System aufstellen, zentrieren, richtige Abstände ermitteln
- Testergebnisse erstellen
Für den ALU-Spherometer (rechts im Bild) gilt a = 50.32 mm, für den blauen Sphärometer (im Bild links) gilt a = 63.2 mm.
Die Messungen haben trotz einer Reihenmessung eine Toleranz so um die 10 mm des zu messenden Radius des Konvex-
Spiegels. Für die spätere Berechnung aber zunächst ausreichend.


ThomasWest
28.12.2005, 10:48
Bescheidene Zwischenfrage.
Was wird in der Formel für b eingesetzt? Das findet sich nicht in der grafischen darstellung?
Rohr
28.12.2005, 16:18
Hallo Thomas,
In der Formel b = 1, ist also der Radius der 2 mm Durchmesser Kugel gemeint.
Bei einem größeren Durchmesser den entsprechenden Radius eingeben. Weil
bei derartigen Messungen bereits ein hundertstel Millimeter eine große Rolle
spielt, ist das nur eine Möglichkeit, den Radius von Kugelflächen zu messen.
Bei Newton-Spiegeln ist das nicht so kritisch. Bei opt. Systemen natürlich zu
ungenau. Da wird man bei Hohlflächen eine Schnittweitenmessung machen,
bei Konvex-Flächen gegen ein Probeglas prüfen etc.
Solche Fragen stellen sich immer dann, wenn man versucht, ein opt. System
wie z.B. ein Maksutov-System auszumessen.