elliptische Planspiegel testen   8. November 2011

siehe auch: http://r2.astro-foren.com/index.php/de/13-beitraege/05-messtechnik-teil-1/50-flat-10-inch-pruefen
und: http://r2.astro-foren.com/index.php/de/14-beitraege/06-messtechnik-teil-2-aufbau-diverser-interferometer/698-f044a-artificial-sky-test-bei-zwei-refraktoren

Elliptische Planspiegel kann man entweder auf Kontakt gegen eine Referenz-Fläche prüfen, dann sollte der Flat aber unbelegt sein, damit ein
kontrastreiches IGramm entsteht. Bei einem beschichteten Spiegel, besonders bei dielektrisch-beschichteten Spiegel, ist ein Interferogramm
zwischen der unbeschichteten Referenzfläche und dem Flat kaum noch erkennbar.
Ein weiteres Problem bei der Prüfung auf Kontakt ist die elliptische Fläche selbst, da die gängigen Auswert-Programme nur "runde" IGramme
auswerten können. Man könnte sich in diesem Fall entweder dadurch behelfen, indem man die lange Achse auf die kleine Achse im Computer
verkürzt - auch dann hätte man ein rundes IGramm. (Im Strahlengang bei 45° Kippwinkel würde man ohnehin einen Kreis sehen)

Einfacher wäre für elliptische Planspiegel ein Test, der der Funktion des Flats im Strahlengang möglichst nahe kommt. Dieser Test ist u.a.
im dreibändigen "Amateur Teleskop Making" beschrieben. (Band one S 42f und S 242f, und im Übrigen George Willis Ritchey zugeordnet
wird.) Ein Flat läßt sich (wie im Band one ausführlich beschrieben) entweder gegen eine Sphäre prüfen, gegen eine Wasser-Oberfläche oder
mit Hilfe einen guten Refraktors. Im Falle der elliptischen Flats empfiehlt sich die Prüfung gegen eine Sphäre. Für diesen Fall bekommt man
ein rundes Interferogramm mit doppelter Genauigkeit, das sich leicht von einem Programm auswerten läßt.

Um aber zu keinem "verstiegenen" Disput anzuregen mit in der Regel praxis-fernen Argumenten, zunächst das Datenblatt von ellipt. Flats,
die von Pörschke bzw. Edmund Scientific als Labor-Qualität zu beziehen sind. Mit einer Oberflächen-Qualität von PV L/8, was einer Wellen-
front-Abweichung von PV L/4 entspricht, liegt man in genau der Toleranz, die für elliptische Flats ausreichend sind, was ich an anderer
Stelle bereits nachgewiesen habe.

In der Regel sind kleinere Flats "genauer" als die größeren Durchmesser, die bei einem Durchmesser von 100 mm kleine Achse dann ca.
1 Kilo-Euro kosten können.




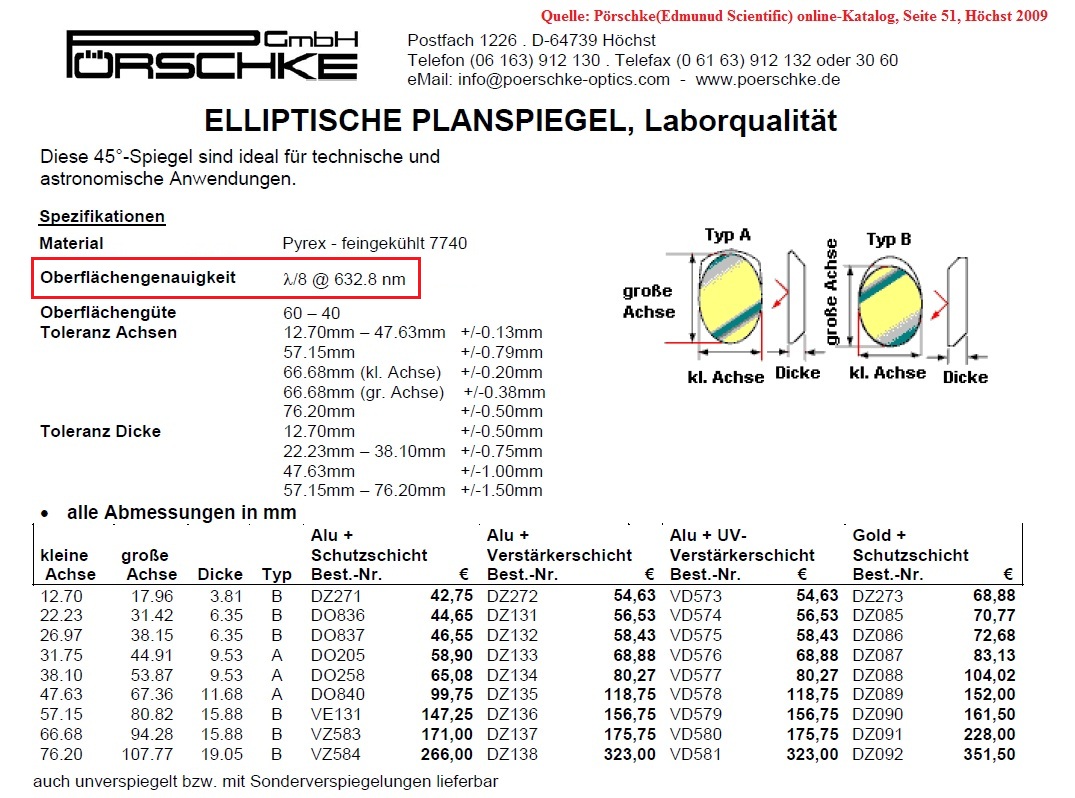
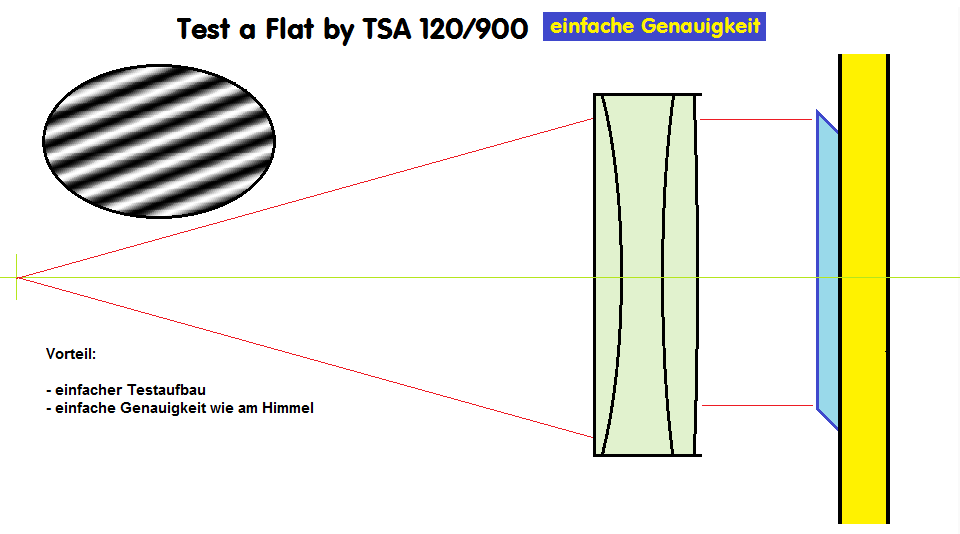
Das Prinzip des Testaufbaus ist einfach: In den konischen Strahlengang wird der Flat genauso in den Strahlengang gestellt, wie er bei einem Newton-Teleskop
auch stehen würde. Da man jedoch die ganze Fläche des Plan-Spiegels messen möchte, rückt dieser entsprechend nahe an die Sphäre. Der Lichtkegel der
Sphäre, aus dem Krümmungsmittelpunkt betrachtet, wird als um 90° umgelenkt. Das Lichtbündel passiert die Planfläche zweimal. Bei einem Durchmesser der
Sphäre von ca. 150 mm bei einem Krümmungsradius von ca. 600 mm hat man also eine kurze Strecke, die wenig Störungen verursacht. Je kleiner der Flat
ist, umso weniger Referenzfläche der Sphäre wird benutzt, und das Ergebnis wird entsprechend genauer.



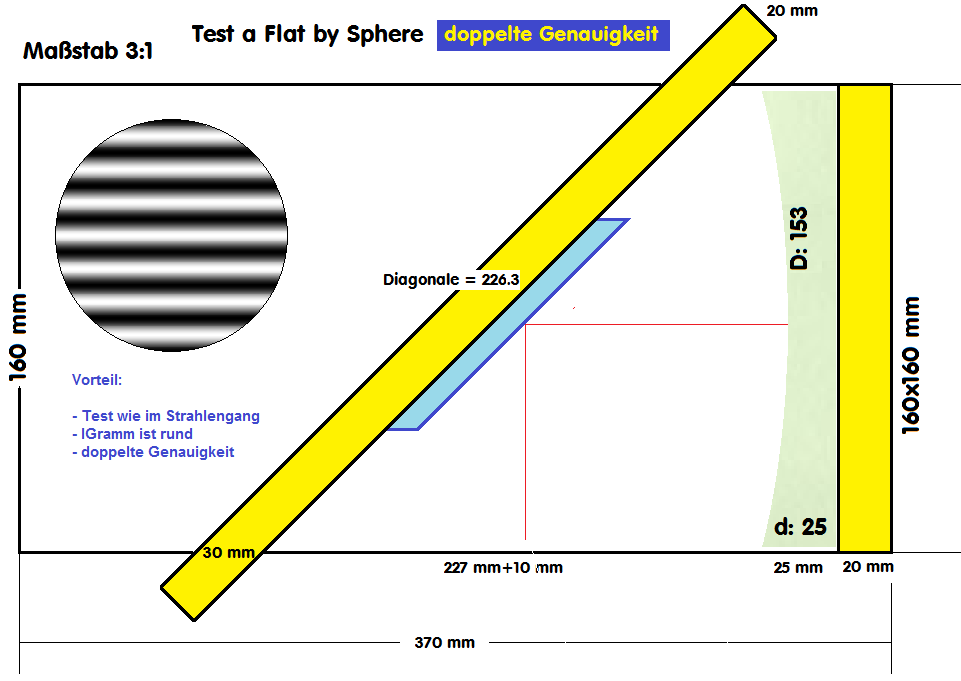
Koma wird man in jedem Fall abziehen können, das Hauptproblem bei Flats ist Astigmatismus, der direkt dem Flat zugeordnet werden kann, aber auch über die
Power entsteht, wenn auf dem Flat ein "Radius" eingeschliffen ist.



Beim Einrichten des Testaufbaus sollte der Flat mittig sein, was man über ein Maßband vom Rand der Sphäre leicht einstellen kann. Daß die opt. Komponenten
spannungsfrei gelagert werden müssen, ist eine Selbstverständlichkeit.



Der gleiche Testaufbau, nur von oben gesehen.



Nun der Vergleich zweier Testverfahren:
Links die Prüfung auf Kontakt, die sich schwer in PV- und Strehl-Werten darstellen läßt. Rechts ein IGramm aus der beschriebenen Testanordnung. Die Werte liegen
unterhalb der oberen Labor-Qualität.



Bei größeren Durchmessern sinkt die Qualität, in diesem Fall ein deutlicher Astigmatismus, der über das Kontakt-Verfahren weniger
deutlich erkennbar ist.



Anzumerken ist, daß eher selten die gesamte Fläche eines ellipt. Flats benutzt wird, während sich aber die Auswertung auf die gesamte
Fläche des Interferogrammes bezieht und damit auf den vollen Durchmesser. Schon wegen der Vignettierung wird man immer einen
etwas größeren ellipt. Flat benutzen. Fangspiegel-Qualität bei einem Newton
der "unbekannte" Fangspiegel - Messung gegen eine Sphäre bei 90° Verkippung

###############################################################################################

70 mm elliptischen Flat prüfen a) doppelter Durchgang gegen Sphäre b) einfacher Durchgang mit TSA 120/900

Ein und derselbe 70 mm Flat wurde auf zweierlei Verfahren geprüft, a) im doppelten Durchgang gegen eine Sphäre, wie oben bereits
vorgestellt, und b) im einfachen Durchgang durch ein TSA-Objektiv 120/900.
Der Testaufbau im doppelten Durchgang gegen eine Sphäre im Winkel von 45° erzeugt ein rundes Interferogramm, das leicht
auszuwerten ist. Dieser Testaufbau entspricht der Position des Planspiegels im Newton-Strahlengang - ein Radius auf der
Planfläche des Flat's würde zusätzlich als Astigmatismus erkennbar sein.

a) doppelter Durchgang gegen Sphäre

Der Testaufbau, wie bereits beschrieben und in der Zeichnung dargestellt.

Der Artificial Sky Test ist ein abgewandelter Star Test, dessen Pinholes zwischen 3 - 5 Mikron im Durchmesser sind. Verformungen zeigen deshalb sehr
genau die optischen Fehler des geprüften Flats an, exakt so, wie man das am Himmel auch sehen würde.

Wegen der 45° Position des ellipt. Flats entsteht ein rundes IGramm, das sich leicht auswerten läßt und zudem den Vorteil der doppelten Genauigkeit
hat. Man erkennt bereits den Fehler an der Verformung der Streifen.

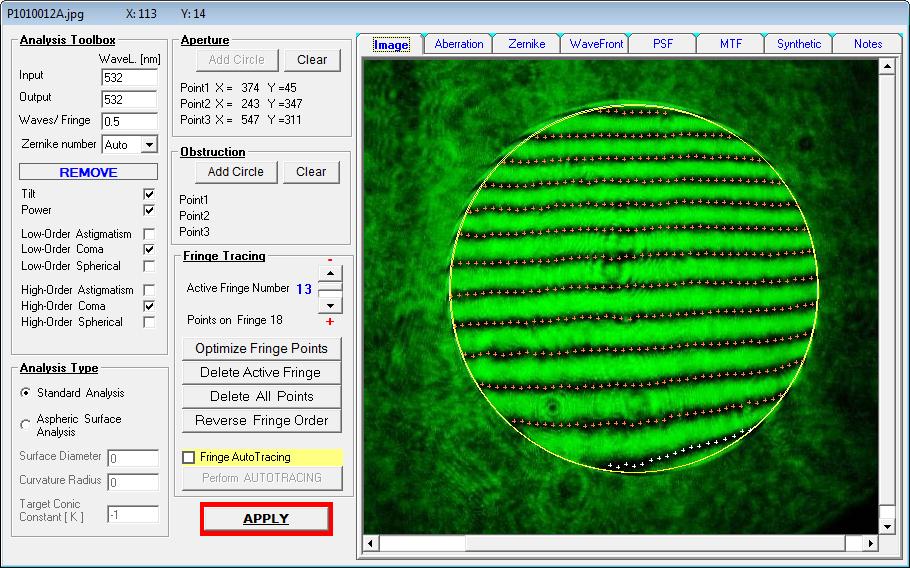
Über die Wellenfront-Deformation läßt sich Astigmatismus als Hauptfehler zeigen

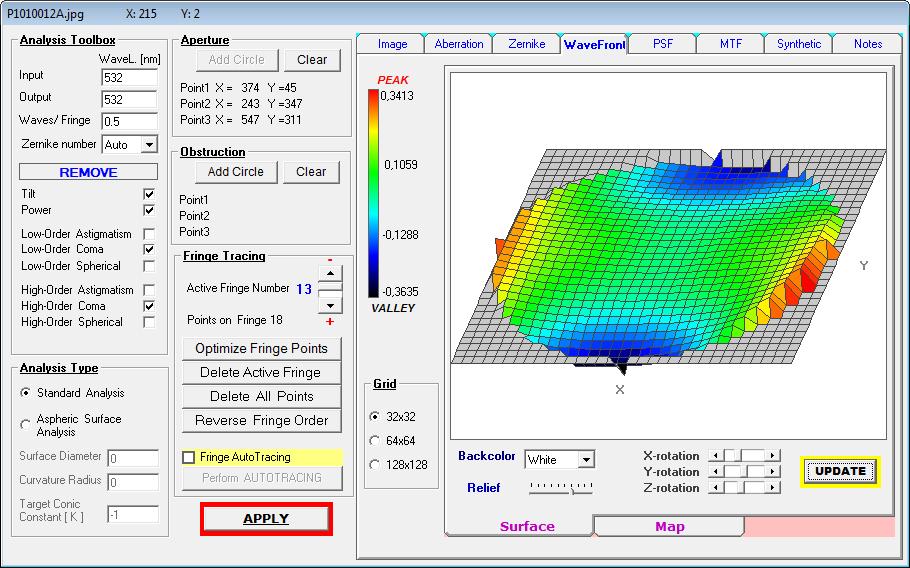
. . . der in seiner Größe von PV L/1.4 der Wellenfront nicht die Vorgaben z.B. von Edmund Scientific erfüllen würde. http://rohr.aiax.de/@FS_15.jpg

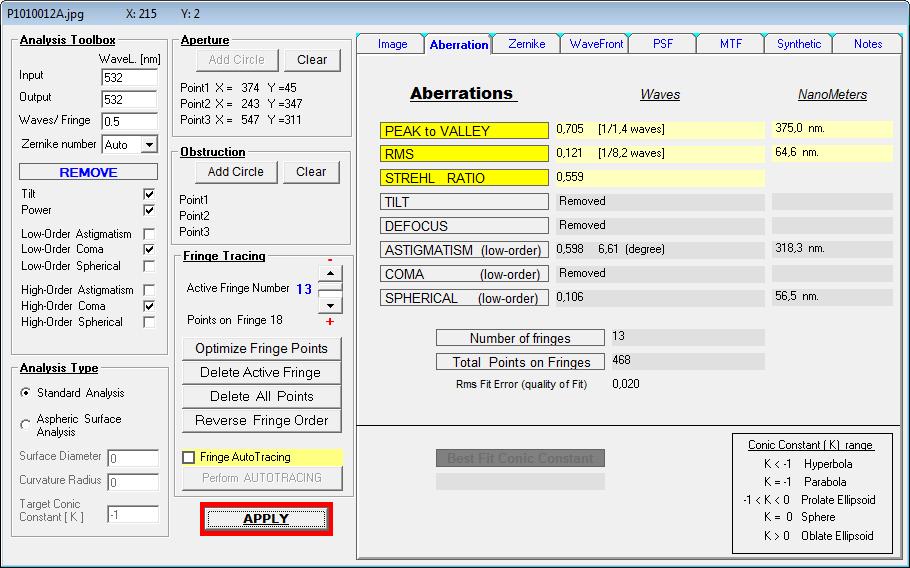
b) einfacher Durchgang durch TSA 120/900

Beim einfachen Durchgang wird in einer Autokollimations-Anordnung nicht der Refraktor getestet, sondern der elliptische Planspiegel. Gegen den
Zeiss Werkstatt Spiegels wird der ellipt. Flat getauscht, sodaß deshalb ein ellipt. Interferogramm entsteht. Der Referenz-TSA muß deshalb auch
hinreichend genau sein, also etwa in der Gegend von PV L/10 der Wellenfront. Der ellipt. Flat wird also in diesem Setup mit einfacher Genauigkeit
geprüft, was jedoch nicht ganz der Situation am Himmel entspricht, weil über die 45° Stellung des Planspiegels im Newton-System die X-Achse
"gestaucht" wird und damit die Unterschiede erklärt beim Artificial Sky Test. In beiden Fällen erkennt man aber den Astigmatismus.

Der Testaufbau im Foto

Und zunächst der Test gegen den Zeiss Werkstatt Spiegel, als Referenz, wie das optimale Prüfergebnis des 70 mm ellipt. Flats eigentlich aussehen sollte.

Mit diesem Bild ist eindeutig, daß derselbe 70 mm ell. Flat auch im einfachen Durchgang Astigmatismus als Fehler anzeigt - nur ist in diesem Testaufbau
die X-Achse nicht verkürzt, weshalb die Situation des Planspiegels nicht ganz exakt wiedergegeben wird: Während im einfachen Durchgang eine eher
regelmäßige Figur entsteht, verkürzt sich über die 45° Stellung die "Spot-Figur" und wird damit dem Artificial Sky Test oben ähnlicher.

Aber auch das IGramm zeigt Ähnlichkeiten mit dem IGramm aus dem oberen Testaufbau, betrachtet man die Streifen etwas genauer. Weil aber
das IGramm eine ovale/elliptische Form hat, ist die übliche Auswertung etwas schwieriger. Man muß also erst die X-Achse so verkürzen, daß
wieder ein kreisförmiges IGramm entsteht. Damit sollte der Test eines ellipt. Flats im einfachen Durchgang genau genug sein, wenn man
eine entsprechend klein dimensionierte Pinhole (5 Mikron) verwendet. Man muß allerdings genau hinschauen.

Durch Stauchung der X-Achse erhält man ebenfalls ein rundes Interferogramm, das in ähnlicher Form den Fehler zeigt. Nun ist der
Scale aber nur 1, im doppelten Durchgang wäre er 0.5. Die beiden Strehl-Ergebnisse stimmen zwar nicht hundert-prozentig überein,
aber auch die Wellenfront-Darstellung zeigt exakt den gleichen Fehler. Insgesamt erscheint der Doppelpaß-Testaufbau realistischer
zu sein.

. . . . .

############################################################################################

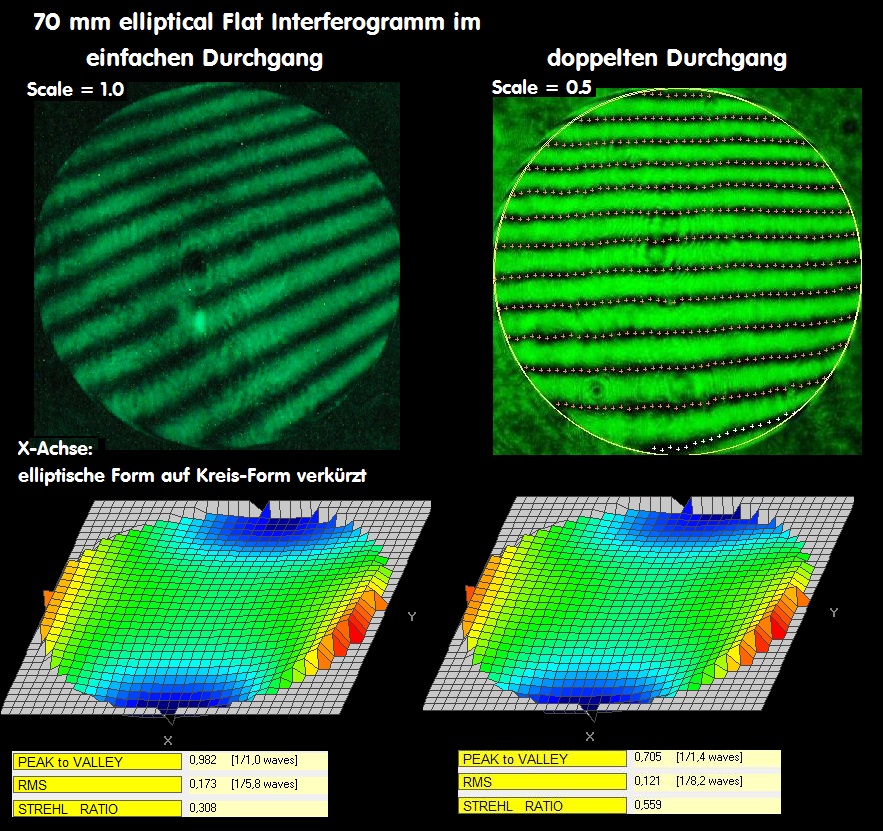
sechs weitere Planspiegel im Test

Die Qualität von Fangspiegels scheint in der Praxis doch nicht so kritisch zu sein - wenn man sich die Erfahrungen von Händlern vergegenwärtigt.
Mithin ein Grund, über diesen Sachverhalt ein weiteres Mal zu berichten.
Zunächst muß man sehr deutlich unterscheiden zwischen Fangspiegeln, die bei der Feldfotografie eingesetzt werden und solchen für visuelle
Nutzung. Anspruchsvoller ist die zweite Variante. Wieviel der im Foto gezeigten jeweiligen Fangspiegel-Fläche wird denn optisch zur Abbildung eines
Punktes überhaupt gebraucht? Und immer nur genau diese Fläche muß einer Qualitäts-Norm von mindestens PV L/4 wave oder PV L/8 surface ent-
sprechen. Das gilt gleichermaßen für die Abbildung auf der opt. Achse, wie für die Sternabbildung im Bildfeld.

An folgendem Beispiel mag dies ersichtlich werden. Bei einem 10" Newtonspiegel f/5 (250/1250) ist bei 1 Meter vom Spiegel entfernt der Fangspiegel
plaziert, sodaß der Fokus mit 250 mm Abstand von der opt. Achse bequem außerhalb des Tubus zu liegen kommt und somit auch noch ein Koma-
Korrektor eingesetzt werden kann. (Dieses Beispiel fixiert nur eine bestimmte Situation und kann entsprechend variiert werden.)

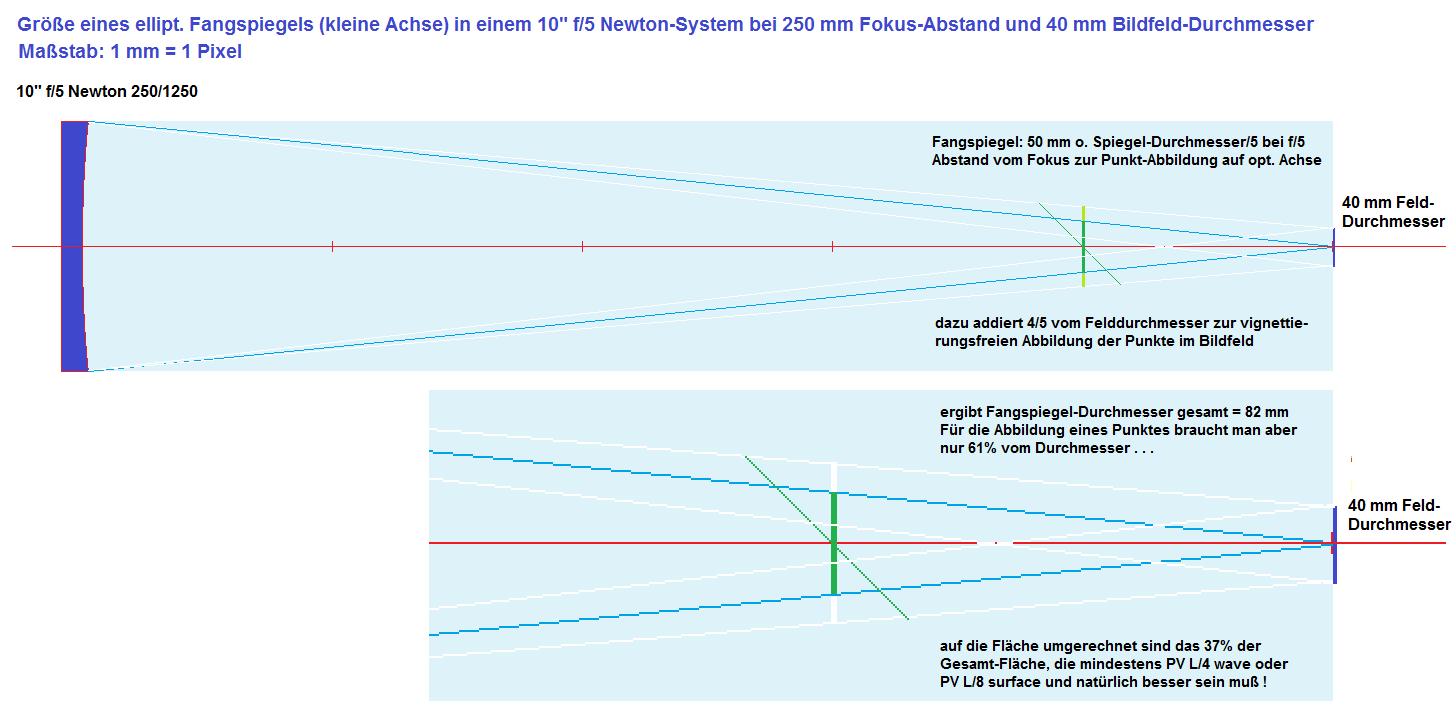
Diese Situation wurde maßstäblich so dargestellt, daß 1 Pixel 1 Millimenter entspricht. Im f/5 Lichtkegel, den dieser Spiegel erzeugt, haben wir bei einem Abstand von
1000 mm vom Newton-Spiegel einen Kegel-Durchmesser von 50 mm, was zur Abbildung eine Sterns auf der opt. Achse völlig ausreichend wäre. Im Bildfeld jedoch
hätten wir schnell die bekannte Vignettierung, die mit Helligkeitsabfall einhergeht. Der Fangspiegel am Ort 1000 mm muß also im Durchmesser größer sein als 50 mm.
Man muß also zunächst das gewünschte Bildfeld im Fokus selbst festlegen. In Anlehnung an das Kleinbildformat 24x36 mm ergäbe sich ein Bildfelddurchmesser
(Diagonale) von ca. 43.26 mm. Zugunsten einer einfacheren Rechnung nehme ich 40 mm als Bildfelddurchmesser.
Damit entsteht ein umgekehrter Kegel vom Fokus-Bildfeld-Durchmesser bis zur Mitte des Newton-Spiegels, der in der Höhe des Fangspiegels nur noch 32 mm Durch-
messer hat. Dieser Betrag muß also zu den 50 mm dazugezählt werden und man bekommt 82 mm Fangspiegel kleine Achse für die Position 1000 Abstand vom HS.
Damit läßt sich vignettierungsfrei das Bildfeld 40 mm im Fokus des 10" f/5 Newton ausleuchten.
Unabhängig davon braucht man für die Abbildung eines einzelnen Stern, wo immer er im Bildfeld ist, weiterhin den Fangspiegeldurchmesser von 50 mm.
Ein Prüf-Protokoll würde sich aber nun auf die Gesamtfläche des 82 mm Fangspiegels beziehen und gibt daher keinerlei Auskunft, wie tauglich dieser Spiegel in einem
bestimmten System überhaupt ist.
.

Diese Frage kann man nun auf mehrere Art beantworten:

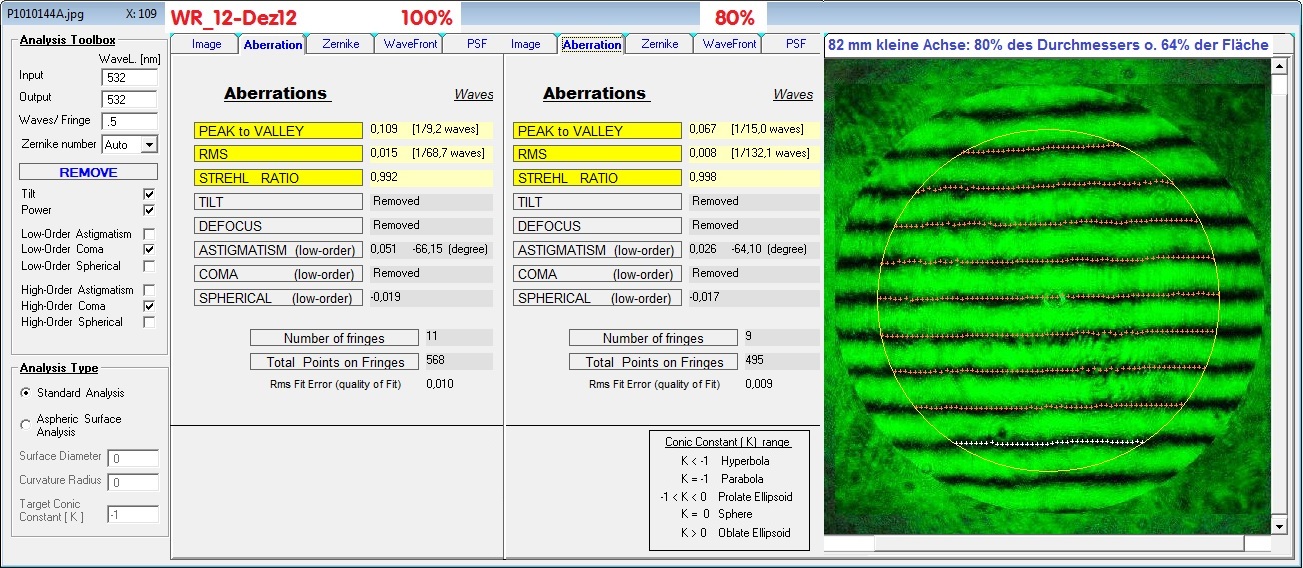
Mit Hilfe des Artificial Sky Testes (siehe die Berichte weiter oben) kann man in die Abbildung bei Höchstvergrößerung untersuchen und zwar a) über den vollen Durchmesser des
Fangspiegels und b) dem tatsächlich benutzen Durchmesser über die Einführung einer Blende. Bei der Auswertung der Interferogramme kann man ebenfalls a) den vollen Durch-
messer und b) einen prozentual verkleinerten Durchmesser auswerten, wobei ich hier von 80% des Gesamtdurchmessers ausgegangen bin, was bereits zu einer erheblichen
Qualitäts-Steigerung führt. Der Artificial Sky Test zeigt sofort einen vorhandenen Astigmatismus, der ein Hinweis auf fehlende Planität darstellt bzw. die Power. Bei mittlerer
Vergrößerung wird man diesen Sachverhalt eher schwer feststellen können.
Da dieser Test abhängig ist vom Radius 600 mm des Kugelspiegels ist, sind die Sternscheibchen-Durchmesser bei einem kleinen Spiegeldurchmesser entsprechend größer nach der
Formel: Auflösung (550 nm) = 138.40/D. Man muß also auch noch den Durchmessers des Fangspiegels berücksichtigen beim Betrachten der Testbilder.

.

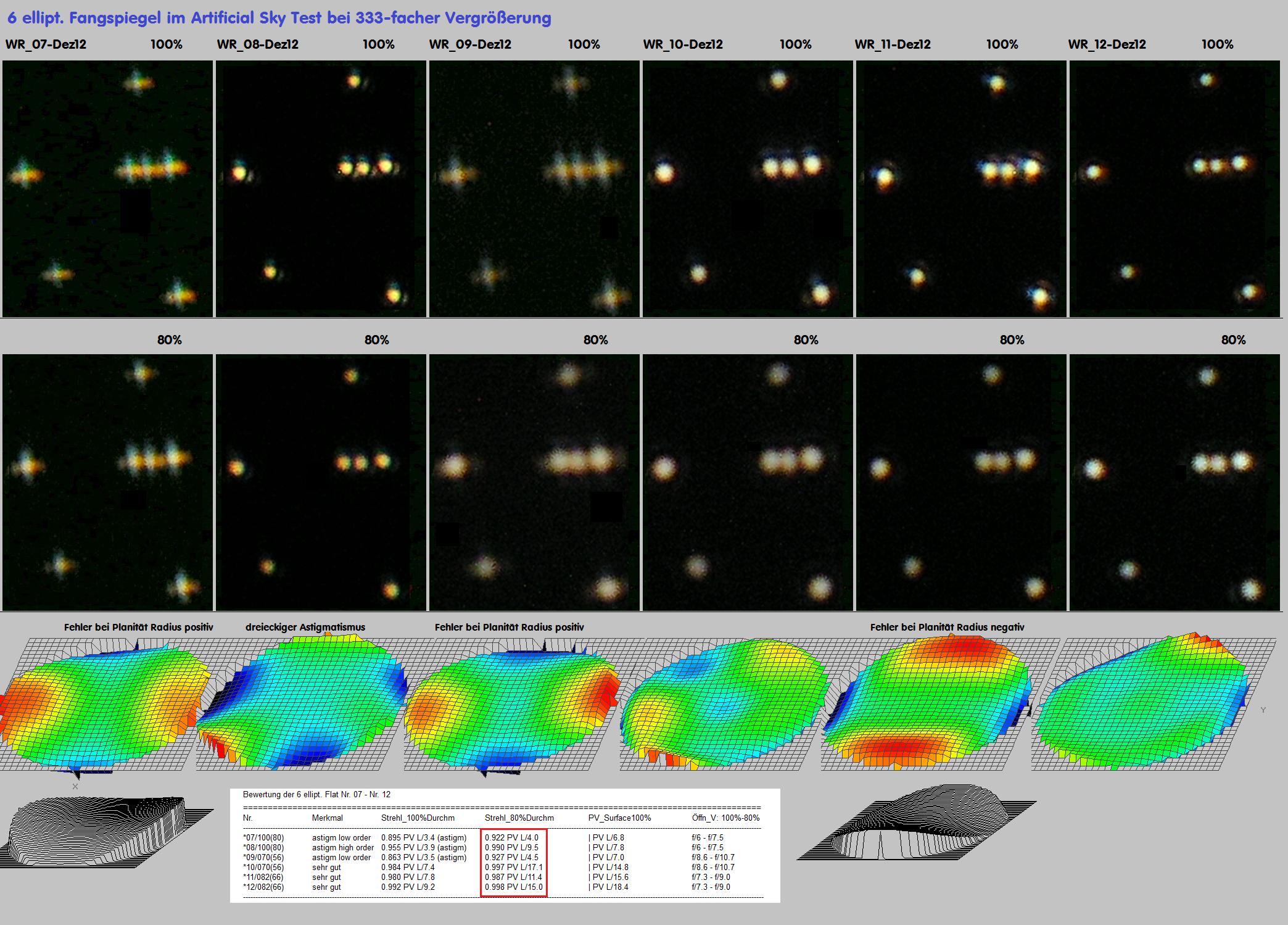
Spiegel Nr. 7, 9 und 11 erzeugt ein großer Radius auf der Planfläche einen Astigmatismus der Grundordnung - bei 7 und 9 wäre es ein positiver Radius, bei Nr. 11 ein negativer Radius. Auch die Strehl und PV-Übersicht zeigt deutlich, wie schnell die Flächenqualität zu nimmt, je kleiner die benutzte Fläche des Fangspiegels ist.

Im nächsten Bild sind die Ergebnisse von 100% Nenndurchmesser zu 80% Nenndurchmesser dargestellt. Der Umkreis von 100% wurde auf 80% reduziert, was nur noch 61% vom
Gesamtdurchmesser entspricht bzw. 50 mm. Auf die Fläche umgerechnet reduziert sich die Gesamtfläche auf nur noch 37% der Gesamtfläche, die man in diesem System tatsächlich
für die Abbildung eines Sternes braucht. Nun so ist es zu erklären, warum Fangspiegel von mittelmäßiger Qualität sich im praktischen Gebrauch sehr unauffällig zeigen.
.

.
.
.