"Foto-Maschine" - Beurteilungskriterien            14. Juli 2012

Bei einem visuell genutzen Teleskop bewegt man sich auf der opt. Achse bzw. im achsnahen Bildraum, weshalb u.a. der Strehlwert als
einfache Qualitäts-Kennzahl herangezogen wird. Weil aber die Strehlfixierung bei vielen Sternfreunden überhand nimmt, geben eine
Reihe von Zertifikaten nur den PV- und RMS-Wert an, der dann erst in eine Strehlzahl umgerechnet werden müßte. Bereits bei visuell
genutztem Teleskopen, noch besser Refraktoren, mutet die Strehlwert-Fixierung wie der Tunnelblick auf eine Optik an. Hier kommt
bereits die Farbsituation ins Spiel und das konkrete Farbspektrum, in dem der Strehlwert festgestellt worden ist. Besonders bei C11s
kommen höchst verschiedene Strehlwerte heraus in Abhängigkeit zur Spektral-Farbe, weil Schmidt-Cassegrain-Systeme für gewöhnlich
einen Gaußfehler haben. C11 - nahezu perfekt auf Grün optimiert; RMS-Wert in Strehl-Wert umrechnen

Eine völlig andere Beurteilungs-Situation entsteht bei fotografisch-genutzten Teleskop-Systemen, wie die vorliegende Kombination aus
APM 107/700 mit dem großen 0.75 x Ricardi-Reducer darstellt, eine sehr überzeugende Lösung, aus einem APO eine "Foto-Maschine"
zu zaubern.

Bereits das Objektiv selbst ist sehr farbrein, wie das Foucault-Bild weiter unten beweist. Durch die Kombination mit dem großen 0.75 x Ricardi Reducer
entsteht eine sehr überzeugende Feld-Korrektur, die sogar über das Kleinbildformat 24 x 36 mm hinausgeht, wie in diesem konkreten Fall. Okularseitig
wird allerdings der Refraktor entsprechend schwerer und der ursprüngliche Tubus mußt auch gekürzt werden, damit das System als Foto-System
funktioniert.

Man hat nun mehrere Möglichkeiten, die richtigen Abstände einzustellen: Entscheidend ist zunächst der richtige Abstand Objektiv - RicReducer, und nur
der ist entscheidend für die optimale Punkt-Abbildung im Feld. Hat man nämlich den optimalen Abstand Objektiv-Reducer, dann muß die Kamera selbst
auf dieses "starre" System fokussiert werden und man bräuchte zwischen Reducer und Kamera einen weiteren Fokuser. Aus diesem Grund kann man
sich auch am Backfokus orientieren, dem Abstand auf der opt. Achse zwischen letzter Linsenfläche zum System-Fokus bzw. Kamera-Chip, oder aber
man orientiert sich an der letzten ReducerFläche, dann wäre davon der Abstand zum Fokus anzugeben. Vorsichtshalber habe ich alle drei Werte ermittelt.
Die Toleranz der Werte dürfte etwa bei +/- 1 mm maximal liegen.
Die Skala auf dem Okular-Auszug muß für dieses Teleskop auf 33 mm eingestellt sein, dann hätte man bei einem Bildfeld-Durchmesser von 45.8 mm
die optimale Abbildung - und das schafft so schnell kein Bildfeld-Korrektor. Ganz entscheidend ist auch der Umstand, daß die Abbildung völlig frei von
Vignettierung ist.

Die Farbsituation mit und ohne Reducer repräsentiert der vergleichende Foucault-Test. Das Grundgerät ist um eine Nuance farbreiner, als die
Kombination mit dem Reducer, was aber bei der Fotografie nicht ins Gewicht fallen sollte.

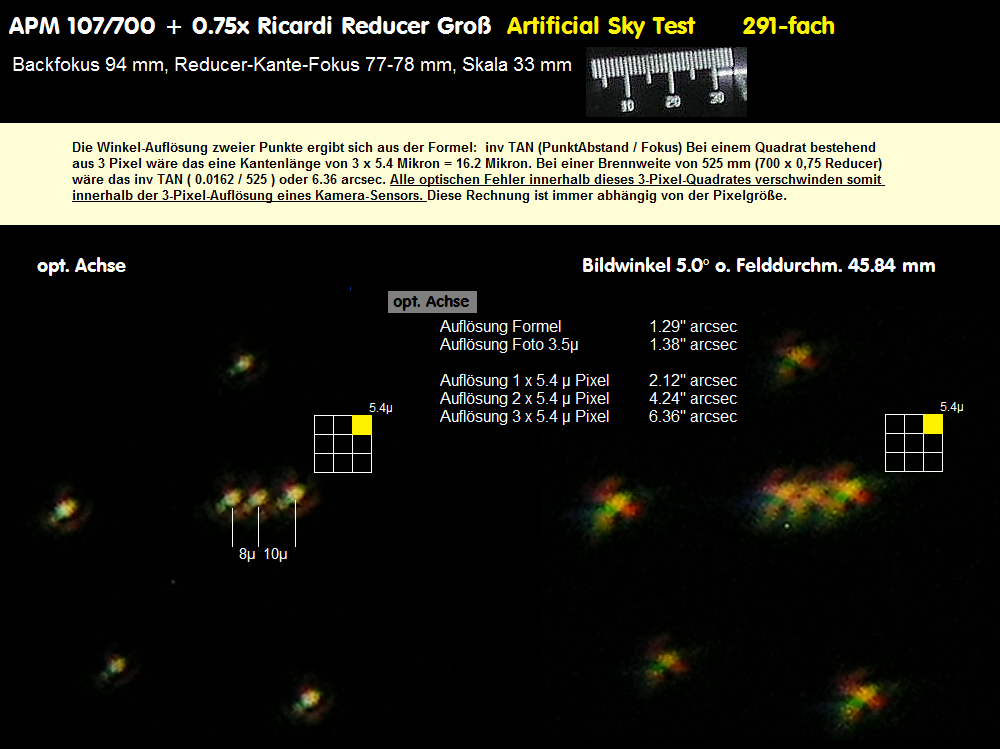
Zunächst wird man den Taschenrechner etwas bemühen müssen: Mit 0.75 Reducer entsteht eine Systembrennweite von nur 525 mm. Benutzt wird
ein Chip, der die Abmessungen des Kleinbildformates hat bei einer Pixel-Größe von 5.4 Mikron. Die im untersten Bild gezeigte Kipp-Vorrichtung läßt
die Situation im Bildfeld darstellen, in unserem Fall führt ein Kippwinkel von 2.5° zu einem Bildwinkel von 5° und damit einem Bildfelddurchmesser
von 45.84 mm, und das ist schon ein beachtlich großer Wert, innerhalb dessen keinerlei Vignettierung erkennbar ist.

Hier geht es also um die punktförmige Abbildung sowohl auf der opt. Achse wie im Bildfeld bei 45.84 mm. Auf der opt. Achse ist das kein Problem.
Erst im Bildfeld entscheidet der richtige Abstand des Reducers über die Bild-Qualität. Hat man den ermittelt, dann entsteht ein großer Widerspruch
zwischen der viel besseren Auflösung, die der Reducer leisten könnte, und der tatsächlichen Möglichkeit, die der Kamera-Chip über die Pixelgröße
zu leisten imstande ist. Rein rechnerisch liegt die theoretische Auflösung im Bereich von einer Bogen-Sekunde, sowohl nach Formel wie nach Foto.

10" GSO RC - Auflösung im Feld perfekt
ATIK 4000-Auflösung und Artificial Sky Test
Wieviel Astigmatismus verträgt die Astrofotografie

Da aber zur Darstellung eines feinen Sternes mindestens 2x2 Pixel, in der Regel 3x3 Pixel und mehr beansprucht werden, reduziert sich die Auf-
lösung im Regelfall auf höchstens 6" Bogensekunden. Zusammen mit den Seeing-Effekten bei einer 10-minütigen Belichtungszeit verschwinden also
viele Fehler, die das System im Bildfeld am Rand noch hat, in unserem Fall etwas Rest-Astigmatismus. Man wird also über das Kleinbild-Format hinaus
feine Sternpünktchen bekommen, die kaum jemand auf ihren tatsächlichen Durchmesser hin überprüft, weil in der Regel die 16 Mikron (3x3 Pixel)
nicht unterschritten werden können. Zu dieser Einschätzung fehlen natürlich noch die Rohbild-Aufnahmen als Beweis-Fotos, die mir der Sternfreund
nachzuliefern versprach.

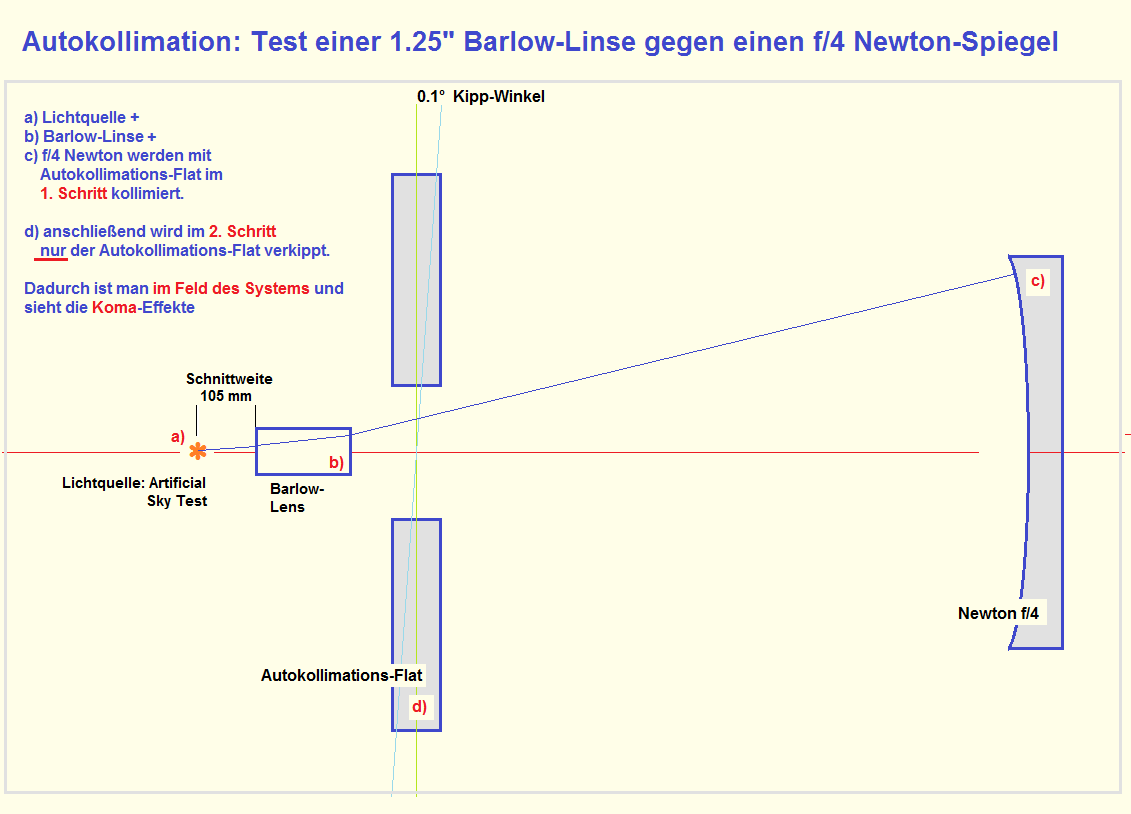
Beim Autokollimations-Setup wird das opt. System vor einem Planspiegel kollimiert. Im Fokus des Systems sitzt die Lichtquelle, die im Doppelpaß
das System passiert und auf dem Rückweg im Fokus beurteilt wird. Dieses Lichtbündel ist parallel zur opt. Achse. Die Abbildung im Feld wird aber
durch Lichtbündel erzeugt, die zur opt. Achse gekippt sind. Diese Verkippung läßt sich dadurch realisieren, indem man den Refraktor vor dem
Planspiegel verkippt, oder aber man verkippt den Planspiegel selbst. Bei einem Refraktor ist die Refraktor-Verkippung zweckmäßiger, beim Newton-
System die Planspiegel-Verkippung.
Mit einer hellen Lichtquelle kann man sich im übrigen die Auswirkung der wechselseitigen Verkippung betrachten, die im Bildfeld eines Refraktors
in der Regel Astigmatismus+Koma erzeugt. Das läßt sich sogar über ein Interferogramm darstellen, ist aber lange nicht so demonstrativ, wie die
Darstellung über einen feinen Lichtpunkt.

Gerrit versprach mir unlängst, in einem Beitrag die physikalischen Gesetzmäßigkeiten eines Kamera-Chips hier darzustellen.
http://rohr.aiax.de/Wie funktioniert der Sensor.mht

http://de.wikipedia.org/wiki/Blooming
.............

##############################################################################################

Hallo Gerrit,

01. Verkippung ist nicht gleich Verkippung. Die Verkippung eines Kamera-Chips zur Bild-Ebene eines fotografischen Systems ist der
Bereich, mit dem Du als Astro-Fotograf zu tun hast. Die Verkippung eines Parallel-Bündels zur opt. Achse eines fotografischen
Systems ist der Bereich, mit dem ich zu tun habe. Beides sind ganz verschiedene Bereiche und die daraus resultierenden Spot-
Diagramm sind nicht vergleichbar.

02. Die bei einem Parabol-Spiegel im Feld erzeugte Koma entsteht über ein Parallel-Bündel, das zur opt. Achse des Rotations-
Paraboloides verkippt ist. Das beweist jedes mit einem Newton (z.B. f/4) erzeugte Astro-Foto. Beweisen läßt sich das auch
über meinen Autokollimations-Test, bei dem der Kollimations-Planspiegel verkippt wird.

Das ist also nun der fotografische Beweis bei hoher Vergrößerung, daß über die Verkippung des 250 mm Durchmesser große Parallelbündels über den Planspiegel tatsächlich die Koma-Figuren entstehen, wie sie jedes optical Design Programm ebenso produziert und im kleineren Maßstab jede Astro-Aufnahme.

Dazu passend im nächsten Schritt Beispiele für Koma-Figuren: Man wird die Ähnlichkeit der Figuren nicht leugnen können.

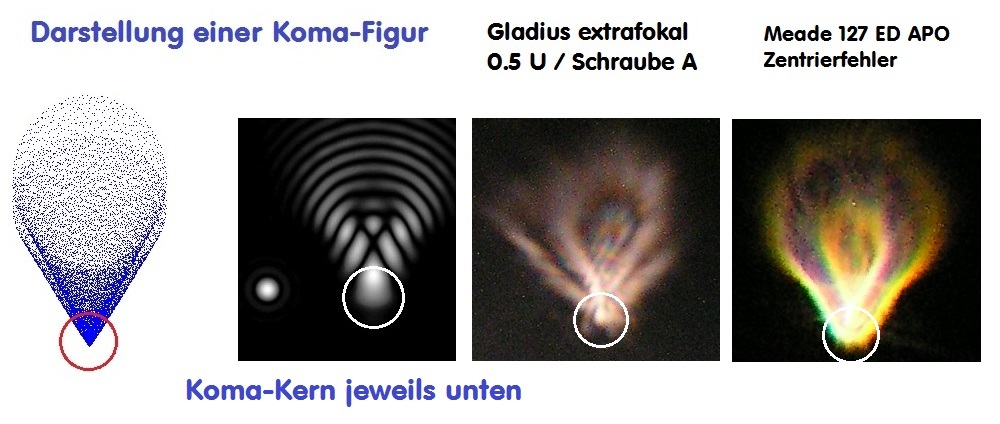
Damit ist das Grundprinzip meines Testaufbaus und dessen Ergebnisse als richtig bewiesen und zwar in jedem Fall für einen Newton-Spiegel.
Wer dieses Verfahren als richtig akzeptiert, muß die Erweiterung dieses Testaufbaus mit einer koma-korrigierten Barlow-Linse oder
eines Koma-Korrektors ebenfalls als richtig akzeptieren. Und das werde ich im Vergleich unterschiedlicher Koma-Korrektoren ebenfalls
untersuchen.

Anmerkung: Bevor wir das theoretisch durchdiskutieren sollen, ist es am einfachsten, den Testaufbau nachzustellen und fotografische
Beweisfotos zu erstellen, nur die sind überzeugend.

Beim oberen Beispiel geht es aber jetzt um die Kombination des APM 107/700 mit dem großen Ricardi Reducer, wie er für die APO-Refraktoren ent-
wickelt worden ist. Auch hier wird verkippt, und zwar der APO + Reducer vor dem Planspiegel, sodaß ebenfalls zur opt. Achse verkippte Parallel-
Bündel entstehen. Und hier zeigt sich nun, daß die Verkippung richtige Ergebnisse liefert: Nämlich bis zu einem Bildwinkel von 5° komafreie
Sternabbildungen. Lediglich etwas Astigmatismus entsteht im Feld dieses Systems, weit unterhalb dessen, was der Kamera-Chip überhaupt
darzustellen in der Lage ist.

##################################################################################################

Hallo Gerrit,

der Unterschied zwischen unseren Fotos besteht darin, daß Du unvergrößerte Rohbilder bekommst,
während in meinem Fall der künstliche Sternhimmel mit der maximalen Vergrößerung bei 291-fach
über das Okular fotografiert wird. Daß deshalb für meinen Fall auch noch Farbeffekte über das Okular
eingeführt werden kann, dürfte klar sein. Entsprechend sensibel ist dann auch die Verkippung des
Okular selbst, und das wäre dann endlich, wie Du die Verkippung auffaßt.

Der Hauptunterschied ist also tatsächlich: Rohbilder gegen Höchstvergrößerung.

Astigmatismus kannst Du bei Deinen Rohbildern deshalb gar nicht mehr sehen, weil in den
Rohbildern kein Unterschied mehr erkennbar ist, zwischen den 3 microns auf der opt. Achse
und den 6 microns bei 42 mm Durchmesser. Das schaffen schon Deine Pixel nicht mehr,
aber mein Okular kann da noch locker mithalten, wie mein Foto weiter oben beweist.

Meine Ergebnisse lassen sich eher mit den Spot-Diagrammen von Massimo vergleichen:
Bei Bilddurchmesser 42 mm taucht beim Spotdiagramm interessanterweise ebenfalls
eine astigmatische Figur auf mit einem Farbquerfehler. Meine Bilder entstanden sogar bei
knapp 46 mm Bildfelddurchmesser . Daraus kann man also keinen Widerspruch konstruieren.
Die Spotdiagramme sind nicht maßstäblich und in der Auflösung relativ klein.

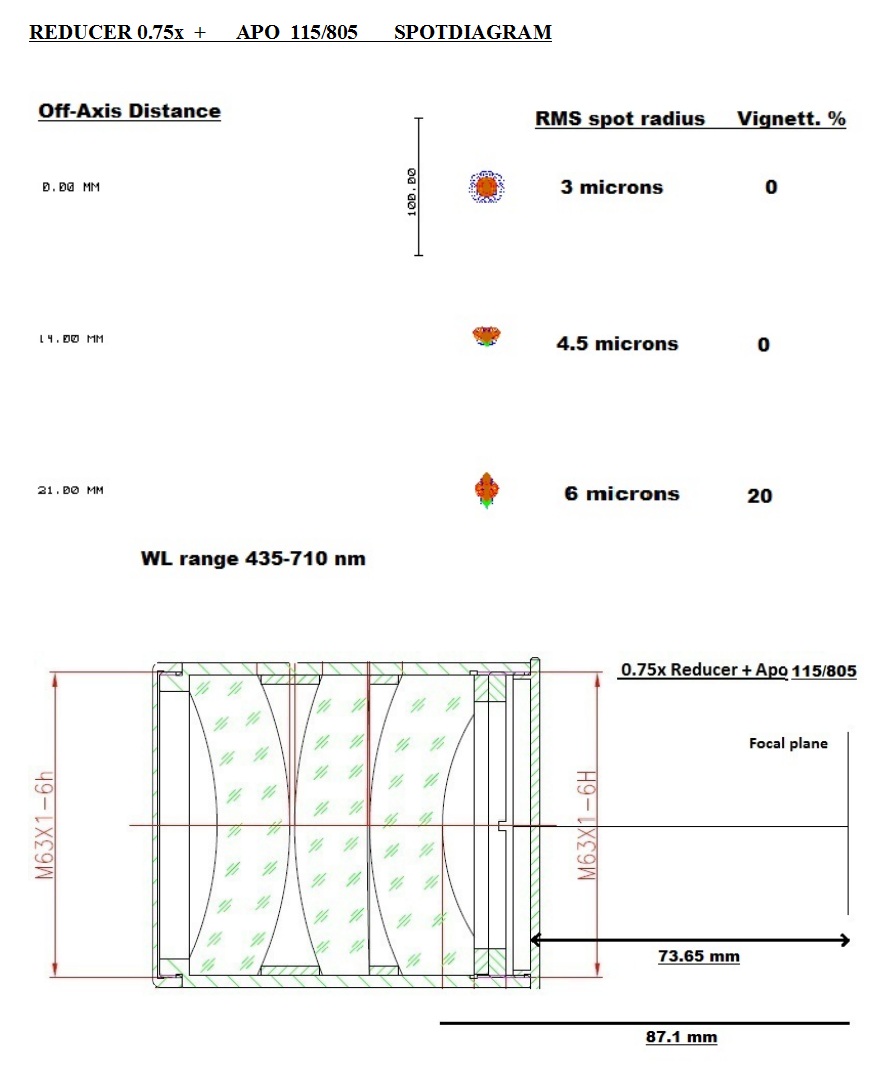
Übrigens auch der Beweis, daß Strehlwerte auf der opt. Achse keine Hilfe sind bei der Qualitäts-Beurteilung fotografischer Systeme.

#################################################################################################

Setzt doch mal das Rohbild rein, damit ich höchstmöglichste Auflösung habe.

Nachtrag zum Thema Verkippung über ZEMAX simuliert

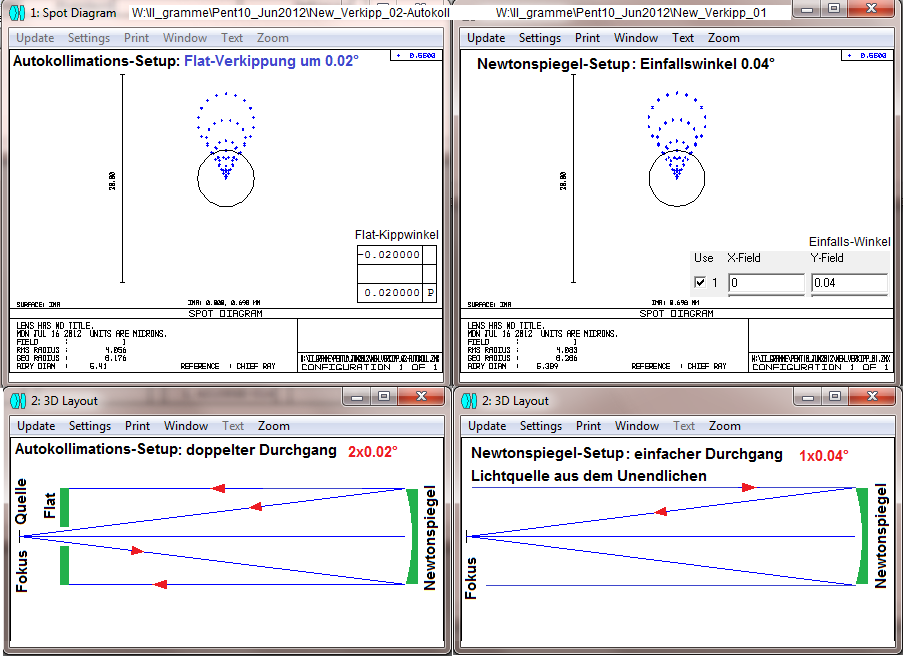
Die Abbildungsfehler(Koma) im Bild-Feld eines Newton-Systems lassen sich mit folgender Methode nachweisen:

Linkes Bild: Man kann einen f4 Newtonspiegel gegen einen Planspiegel mit Bohrung stellen, dann hat man ein Autokollimations-Setup,
auch Doppelpaß genannt mit, weil das Licht 2x den Newton-Spiegel "passiert". Den Planspiegel kann man um 0.02° verkippen, und
man erhält eine Koma-Figur. Logisch ! Das Parallel-Lichtbündel fällt 2x, also auf dem Hin- und Rückweg, auf den Newton-Spiegel und
weil der Planspiegel um 0.02° verkippt ist, bekommt das urprüngliche Bündel, das auf dem Hinweg noch parallel zur opt. Achse ist,
über den Planspiegel die doppelte Verkippung von 0.04° (Einfallswinkel = Ausfallswinkel). Der damit entstehende Einfallswinkel von
0.04° erzeugt die bekannte Koma. Man sieht es an der Figur.

Rechtes Bild: Nun kommt aus dem Unendlichen ein Parallel-Lichtbündel. Auch dieses beschreibt einen Einfallswinkel zur opt. Achse
von diesmal 0.04°. Auch hier entsteht Koma und logischerweise die gleiche Koma-Figur wie im linken Bild.

Es ist also egal, wie ich die Koma-Figur erzeuge: Entweder ist der Newtonspiegel zum ankommenden Parallel-Bündel
verkippt, oder aber das Bündel wird über den Planspiegel verkippt. In beiden Fällen ist der Einfallswinkel 0.04° und deshalb
entsteht der gleiche Koma-Betrag, und man sieht ihm nicht mehr an, wie er entstanden ist.
Das ist das Prinzip meines Testaufbaus zur Darstellung der Koma im Feld.

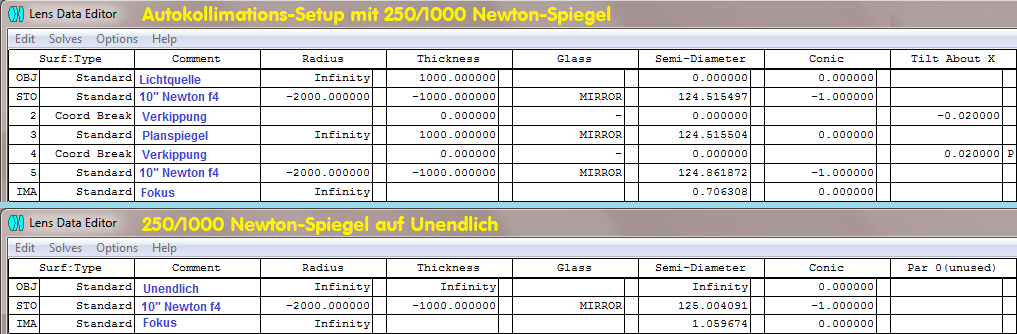
Was nun mit einem einfachen Newton-Spiegel geht, geht auch über die Erweiterung durch eine Barlow-Linse oder irgendein
anderes opt. Element, das natürlich zum Newton-Spiegel auf der opt. Achse vorher kollimiert/justiert werden muß.
Verkippt man nun den Planspiegel, dann ändert sich an der Einheit Newton-Barlow-Linse nichts. Lediglich das Parallel-Bündel
wird zur opt. Achse verkippt eingespiegelt und verursacht je nach Design die entsprechenden Spot-Diagramme. Wenn es sich
nun um eine angeblich koma-korrigierende Barlow-Linse handelt, dann muß man das über die Verkippung sehen können. Dies
umso mehr, wenn eine Barlow bei gleicher Verkippung nur den halben Koma-Anteil zeigt wie die hartnäckig als komakorrigie-
rende Barlow deklarierte. Handelt es sich um einen sog. Koma-Korrektor, dann muß die Komakorrektur des opt. Elementes
ebenfalls zu sehen sein. (Auf dem Hinweg würde dem Parallelbündel über den Komakorrektor eine neg. Koma aufgedrückt, die sich
nach der Verkippung über den Flat auf dem Rückweg mit der normalerweise entstehenden Koma kompensiert und damit im Idealfall genauso
verschwindet, wie bei einfachem Durchgang am Himmel - wenn der Korrektor funktioniert.)

Wenn nicht, dann stimmt in der Kette Design bis zur Fertigung irgendetwas nicht.

Diese logische Beweisführung sollte man eigentlich nicht anzweifeln können. Die linke Simulation entspricht meinem
Autokollimations-Setup, die rechte Simulation entspricht Deiner Astrofotografie. Es müssen deshalb zwingend ähnliche
Ergebnisse herauskommen.